基于模糊粒子滤波的视频跟踪方法研究

张广法, 刘毅

（中国人民解放军91880部队，山东胶州 266300）

0 引言

摄像机阵列装置目前已经达到了低消耗和电荷耦合，其计算能力越来越强且易于实现[1]。因此为了提升监控效果，在很多应用环境中以增加摄像机的数量来增强监控的性能。但是，对于普通的监控应用系统而言，增加摄像机数量的同时必将导致数据的大量增加，并且同时增加了操控人员以及存储设备的负荷。而且这样的方法也并不能保证对敏感区域进行长时间有效的监控。实际应用中，能够对运动目标保持较好的检测和跟踪是一个好的智能监控系统必须具备的基础性能之一[2]。

针对复杂条件下的视频目标跟踪问题，本文提出了一种模糊粒子滤波算法，主要的研究内容包括以下几点：1)采用模糊推理技术有效解决颜色特征向量对光照突变和相似背景条件下的观测模糊性，建立模糊颜色直方图方法；2)针对背景建模的难点，提出一种自适应高斯混合背景建模方法。针对每一个像素进行单独建模为k个高斯分布的混合模型，能够自适应地处理光照突变等复杂光照条件下的目标跟踪问题；3)采用模糊量测作为观测似然函数进行粒子更新，并对不同的模糊量测进行对比分析，探索不同环境下最优化的模糊量测信息；4)将模糊量测技术引入到视频多目标跟踪领域中，实现不同场景中的多目标有效跟踪。

1 智能视频监控跟踪方法

基于静止摄像机的彩色视频图像多目标运动检测跟踪问题，在室内和室外环境下的处理方法是基本相同的，本章考虑了一个基于自适应的高斯混合模型方案，对背景进行自适应的建模处理。其中模糊处理技术可以用来对目标的后验概率密度进行实时估计处理，并在多目标关联问题中实现有效的应用。基于此点，本章提出了一种基于模糊推理技术的模糊推理粒子滤波算法，对基于不同模糊量测的视频跟踪效果进行综合对比，并给出相应的跟踪结果。

1.1 背景建模

在文献[6]中，已经详细介绍了采用Stauffer–Grimson算法和背景建模方法对运动目标进行分割的具体实现步骤，关于每一帧图像中的每一像素的强度值Xt=I(x,y,t)可以通过一个具有k个高斯分布的混合模型进行近似处理， 并在本文中建立了基于观测信息的模型自适应更新机制。

在时间t时刻，{X1,X2,..Xt}表示特殊像素的历史信息，通过移动目标在场景中的变换，当相应变量发生改变的时候，可以依靠每一种高斯分布的持久性和方差对特殊像素进行前景和背景分割。将这些自适应的高斯混合分布模型视为最有可能的背景过程，其中与“背景”高斯分布最不匹配的像素被分组为前景目标，将目标的观察概率模型表示为：

其中，k是高斯分布的数目，ωi,t是时间t时刻混合高斯模型中第i个高斯分布的相关权重估计，且 ωi,t=1，mi,t是时间t时刻混合高斯模型中第i个高斯分布的均值，Σi,t是相关的协方差。假设有 Σ= σ2I，其中 σ2是方差。η是文献[6]中定

i,ti,ti,t义的高斯密度函数。t时刻第k个分布的权重ωi,t可以通过下式进行自适应更新：

上式中α被定义为学习率，且 Ki,t= ｛ 0,1}，其中，1表示已经匹配的模型，0表示剩下没有匹配的模型。其中不匹配分布的均值mi,t和方差保持不变，具体的参数随着最新观测信息的到来进行实时的更新，具体的更新公式如下：

为了实际应用的需要将相应的结果近似为α。在实际的试验中，如果某一个像素经常出现并且基本保持不变的话，就将其视为背景。为了进行有效的建模，采用ω/σ对建模中采用的高斯模型进行管理。当前分布的增益获取更多的证据或者是方差减少的时候，ω/σ的值就会增加。这种方式的管理是一种很有效的在线管理方法，采用开始-结束的方式，根据相应的权重高低比例，使得最有可能成为背景的分布仍然在顶部，最没有可能成为瞬间背景的分布趋向于系统低端，并且最后将被新的分布所取代。为了有效区分背景，这里通过整体考虑系统的先验概率T的方法来区分背景，当第一个关于状态聚集的B概率达到了T的时候就被认为是背景的一部分，其具体的表达式如下：

其中，T被解释为背景的应该占据的最小比例部分的量测值。为了跟踪多个目标，将检测到的前景目标用于本文提出的模糊PF方法。

1.2 模糊颜色特征

在FCH方法中，通过模糊度隶属函数建立相应的直方图方格(bin)，其中，FCH 通过F(I) = {f1,f2,...,fj}表示，这里fj通过以下函数进行定义：

ui,j是第i个像素在第j个颜色bin中的值，pi是像素的概率，从图像中选择的也就是第i个像素，N是像素的综合。 鲁棒的颜色直方图首先通过量化在RGB颜色空间的n个颜色bins决定。更进一步地，为了减轻 RGB颜色空间的不均匀性，每一个像素的颜色从 RGB空间映射到CIEL a*b*颜色空间。本文采用基于c均值计算的FCM颜色直方图转换，其中，c要小于n. 这里c的粗糙颜色bins代表模糊聚类中心，而且通过利用 FCM 技术，使得每一个好的（细小的）颜色bin的结构通过粗糙的颜色 bins决定。对于同一的颜色空间，FCM为最小化目标函数，其具体的决定公式如下式(3.10)所示：其中，M是一个成员函数矩阵， F ={f1,f2,...,fc}T是未知的聚类模型的向量，ui,j代表第i个相应于集合X={X1,X2,..Xt}的成员函数，该集合属于第j个聚类。指数m控制着成员函数的模糊程度通过c聚类进行分享。聚类中心和成员函数值通过式（8）和式（9）以下表达式进行迭代计算。具体的 FCM计算可以通过 Fc×1=Mc×n×Hn×1表示，其中，Hn×1的n个bin 是RGB空间到CIEL a*b*空间转化的细小颜色直方图，Mc×n是基于ui,j的成员矩阵代表第i个详细颜色bin，在实际应用过程中，这些取值均可以采用离线状态预先计算出相应的结果。

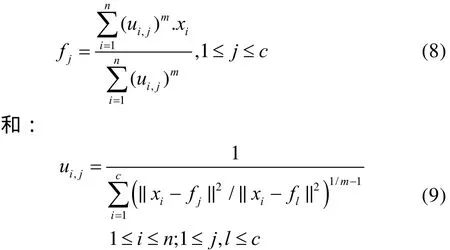
1.3 模糊量测信息

从模糊直方图中得到的图像特征集合可以形成不同的模糊量测值，在基于模糊量测技术的视频目标跟踪中，模糊量测信息已经被广泛应用于多目标之间的相互关联。本节主要讨论当前采用的几种重要的模糊量测信息，并给出详细的计算表达式。

1) 基于最大最小比率的量测。基于最大和最小成员值的模糊量测。在两幅图形中，采用第i个直方图相应于成员值的变量ui,1和ui,2进行相似性计算，在完全相似的情况下其值为 1，具体的计算式如下：

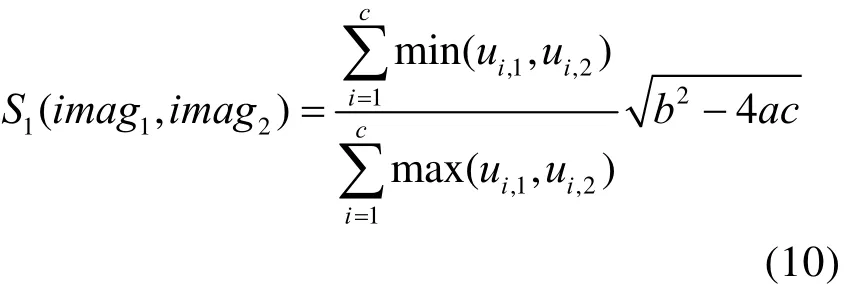
2) 基于对比的深度增强量测。该量测信息主要是基于对比的深度增强量测信息，对于相同的场景其相似值为 1，其中 | ui,1-ui,2|为 0，具体的计算表达式为：

3) 基于归一化的绝对差的量测。这种量测是基于从模糊直方图计算两个成员函数值归一化的绝对差。这种量测可以实现对图像序列中的目标进行实时的检测，其具体的计算表达式为：

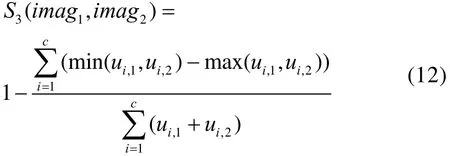
4) 基于模糊散度的量测。两个模糊直方图之

间的模糊散度量测可以表示为：

根据文献[3][4]的描述，imag1,imag2之间的相似性与散度是成反比的。散度越小，两幅图形就越相似，反之相似度越低。对于两幅完全相同的图形，其散度为0。

5) 基于集论方法的量测。Tversky借鉴人类的相似感知特性提出了一种特征对比模型，将度量空间的点集考虑为二进制的点特征，该概念被扩展为彩色图像之间的相似性。文献[7]提出了一种进行图像区域特征抽取的更具普遍意义的Tversky索引(Tversky index, GTI)量测。其具体的计算表达式为：

GTI的主要思想就是基于人类的感知特性提供量测信息的定向评价，其中α和β的值决定了两幅图像有差别的特征相对重要性。

2 实验与结果分析

为了验证本文算法的有效性，该部分采用Internet提供的标准测试序列进行了多组实验分析，主要进行了室内与室外两种不同情况下的跟踪测试，具体的测试内容主要包括不同光照条件下的跟踪结果等。本章算法在CPU 1.5 GHz的PC处理器上运行。其中室外的测试序列主要是针对两个运动的男孩，并且在视频序列中出现交叉现象且出现消失现象的跟踪，具体如图1所示。其中视频的获取的帧率为25 ft/s，检测到的前景如图2所示。

为了进行有效的前景分割，首先要对背景模型进行估计，其中的第一步就是对背景建模进行有效的初始化处理，在进行跟踪初始化的时候参量的第一次初始化主要取决于背景的检测结果，在系统出现明显光照改变的情况下，参数需要重新设置，目前通用的方法就是采用独立的光照检测器对光照突变环境进行实时的检测处理并给出判断标准。

为进一步检验本文算法的有效性，在实验中分别基于本文方法对夜间公路上行驶的车辆和室内走廊中交互运动的行人进行了相应的检测跟踪，图3到图5给出了采用本文方法中利用FGTI量测信息的跟踪结果，其中不同的α取值可以获得不同的跟踪效果，具体的跟踪效果如图4～图6所示。从图中可以看出，在基于相同的测试序列、相同的观测信息时，本文方法表现出了更好的跟踪效果和跟踪鲁棒性。

3 结论

本文针对光照突变等情况下的目标鲁棒跟踪问题，提出了一种基于模糊推理技术的模糊粒子滤波算法，该算法采用5种不同的模糊量测技术，根据不同的场景环境需求，将相应的 RGB颜色空间模型映射到CIEL a*b*颜色空间进行运算，并提出了基于模糊颜色直方图的观测信息。实验证明了本章方法具有较好的抗光照突变特性和多目标关联特性，是一种有效的视频序列目标跟踪方法。

[1]曲彦文，张二华，杨静宇. 改进的无迹粒子滤波算法[J]. 控制理论与应用， 2010, 27（9）：1152-1158.

[2]余孟泽，刘正熙，骆键等. 基于改进粒子滤波的鲁棒目标跟踪算法[J].光电子·激光, 2011,22(5):766-770.

[3]龚俊亮，何昕，魏仲慧等. 采用改进辅助粒子滤波的红外多目标跟踪[J]. 光学精密工程, 2012,20(2):414-421.

[4]Chunlin Wu, Chonzhao Han. Quadrature Kalman particle filter[J]. Systems Engineering and Electronics,2010, 21(2): 175-179.

[5]石勇，韩崇昭. 自适应UKF算法在目标跟踪中的应用[J]. 自动化学报，2011, 37（6）：755-759.

[6]Wang Chong, Wang Wenyuan. Links between PPCA and subspace methods for complete gaussian density estimation [J]. IEEE Transactions on Neural Network,2006, 17(3):789-792.