电弱磁单极子的存在唯一性
祖定利
(承德石油高等专科学校社科与数理部,河北承德 067000)
电弱磁单极子的存在唯一性
祖定利
(承德石油高等专科学校社科与数理部,河北承德 067000)
电弱磁单极子在电弱唯像论中有重要的应用。采用动态打靶的方法证明了在电弱理论下这种磁单极子的存在唯一性,同时也得到了解在原点的渐近估计。
磁单极子;动态打靶;存在唯一性
1 问题提出
自从Dirac[1]提出了磁单极子的概念以来,磁单极子便一直被广泛认为是理论物理中引人入胜的话题。在文献[2]中,Cho和Kim利用球对称假设及正则化算子把标准Weinberg-Salam模型的拉格朗日算子:
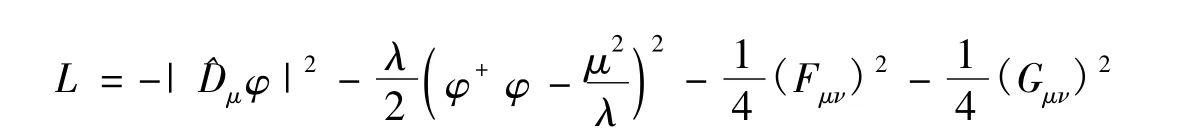
转化为下列的方程组:

这里sin2θw=0.232 5,θw为Weinberg角。同时,他们用数字模拟法证实这种电弱磁单极子的存在性。这篇文章的目的是用动态打靶法[3]证明了这种电弱磁单极子是确实存在且唯一的。
2 数学结构分析
本文考虑方程组(1)在变换(f,eρ)→(f,ρ)情况下的一般情形,此时方程组变形为:
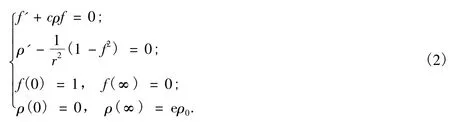
由常微分方程初值问题解的存在唯一性定理可知,对任何r,f(r)>0,事实上,0<f(r)<1,这是因为由方程组(2)的第一个方程及初始条件可得f(r)=e-∫r0cρ(r)dr> 0 。又由方程组(2)的第二个方程可知,若f(r)≥1,则ρ'(r)≤0。当ρ'(r)=0时,这和ρ(0)=0,ρ(∞)=eρ0矛盾;当ρ'(r) <0时,由于ρ(0)=0,所以ρ(∞) <0,这也和边值条件矛盾。因此0<f(r)<1。于是,令U(r)=lnf(r)由方程组(2)变为下列形式:

这个方程是一个半线形方程,而且较难处理,为此我们令r=et,则方程组(3)变为:
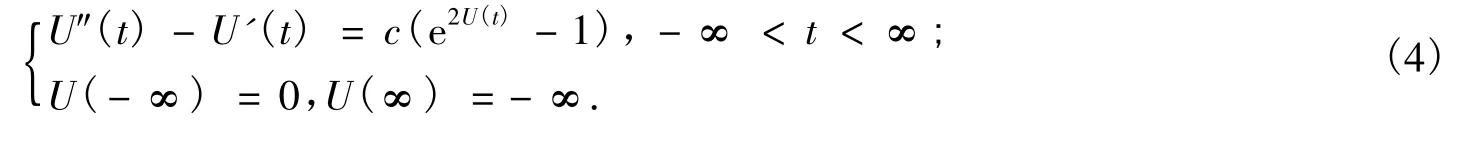
3 数学证明
利用动态打靶法解决问题时,首先要考虑如下初值问题:
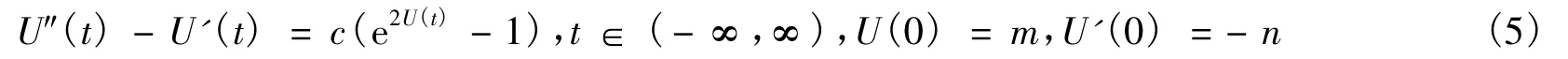
因为要寻找一个负值解,所以我们自然可以合理地要求:
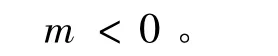
在此假设下,我们将要证明:当选择适当的n>0时,我们可以得到(4)的一个解。从所讨论的问题的结构可以看出,边界条件是U(-∞)=0是一个重要的部分。所以先讨论t→-∞的情况.作变量替换:s=-t并将(5)式在 -∞ <t≤0改写成如下形式:
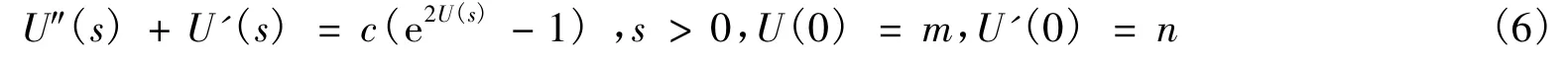
其中U'表示可逆变量s的微分。同时,在不引起歧义的时候,在也用Us表示dU/ds。对于一个m<0,用U(s;n)来标记(6)在解的存在区间上的唯一解。
现在要对(6)式使用打靶分析法。首先构造三个互不相交的集合B-、B0和B+:

引理1:R=B-∪B0∪B+。
证明:如果n∉B-,于是对于所有的s>0,Us(s;n)≥0。假设存在一个点s0>0使得Us(s0;n)=0,那么,由U=0是(6)方程的一个平衡点且方程的平衡点不可能在有限点打到,知U(s0;n)≠0。对于(6)式中的方程,由U(s0;n)≠0但Us(s0;n)=0可知,在s=s0处,U″>0与U″<0中的必有一个成立。于是,存在一个s<s0或s>s0,使得Us(s;n)<0。这显然与假设n∉B-相矛盾。于是,对于所有的s>0成立Us(s;n)>0并且n∈B0∪B+。所以有R=B-∪B0∪B+。
引理2:集合B-和B+均为非空开集。
证明:首先证明B+是非空的集合。
由(6)式方程可知:
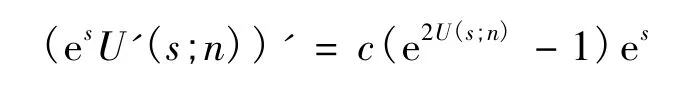
在[0,s]上积分,于是有:
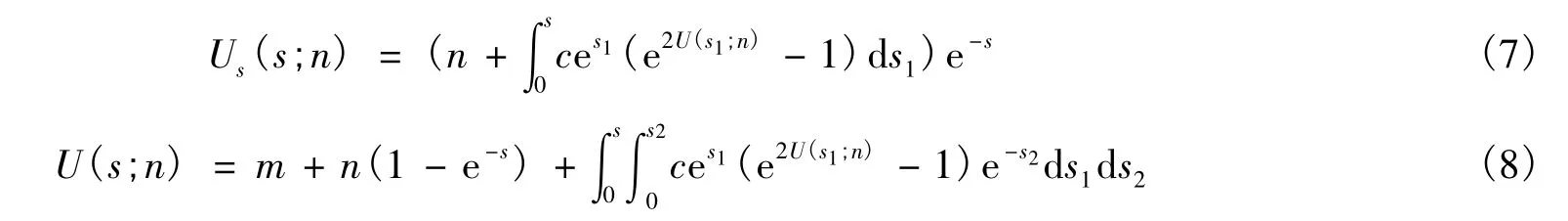
对任意固定的s0>0,选取n>0足够大,必然成立以下两式:
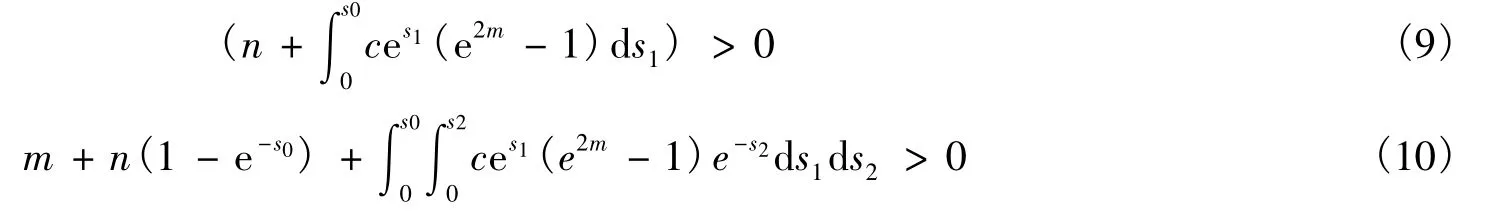
根据(7)-(10),利用达布定理可得:
∃s1∈ (0,s0),s.t对 ∀ ∈[0,s1],均有 Us(s;n) > 0和 U(s;n) < 0且 U(s1;n)=0。
所以,对任何s>s1,都有:
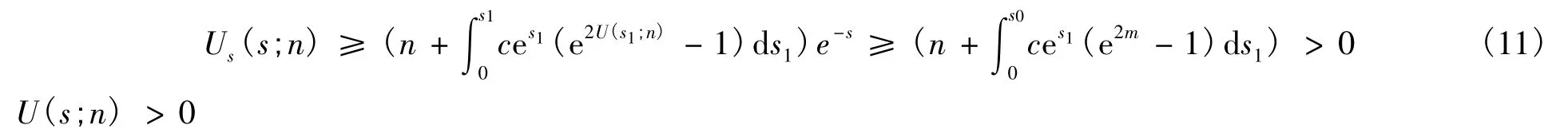
故,B+是非空的集合。
下证:B+是开集。
假设 s0∈B+,则∃s0> 0,s.tU(s0,n0) >0。于是当n1→n0时,对∀s∈[0,s0],均有U(s0;n1)>0和Us(s;n1)>0。由(11)式知,对∀s>s0,均有:Us(s;n1)>0。故B+是开集。
同理可证集合B-均为非空开集。
引理3:B0为非空闭集。而且如果n∈B0,那么对于所有的s>0成立U(s;n)<0。
证明:由引理2及连通性定理可知B0为非空b闭集。为证明第二部分,我们假设成立有一个s0>0使得U(s;n)=0。由于对于所有的s>0成立U(s;n)≤0,于是,U在s0>0处达到局部最大值。并且成立Us(s;n)=0这显然与B0的定义矛盾。证毕。
引理4:集合B0事实上是一个单点集。换句话说,正确的打靶值实际上是唯一的。
证明:假设在B0中存在两个不同的点n1和n2,于是,U(s;n1)和U(s;n2)分别是相应的(7)式的解。
构造函数W(s)=U(s;n1)-U(s;n2),则此函数满足边界条件W(0)=W(∞)=0和方程:
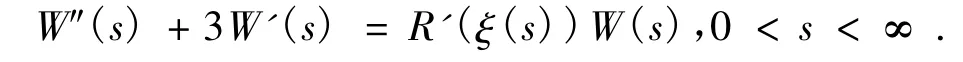
其中 ξ(t) 在 U(s;n1) 和 U(s;n2) 之间,R'(ξ(s))=2ce2ξ(s).对 W″(s)+3W'(s)=R'(ξ(s))W(s)应用最大值原理可知:W(t)≡0这显然和假设n1≠n2相互矛盾。证毕。
4 渐进估计
若假设n∈B0,则当s→∞ 时,必有U(s;n)→0。故在U(s)=0附近,U″(s)+U'(s)=c(e2U(s)-1)≈2cU(s),所以该方程可线性化为:
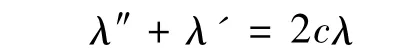
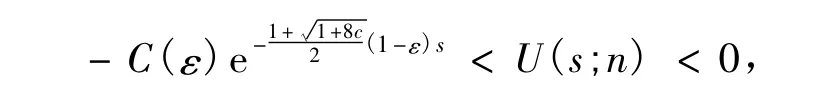
于是有:
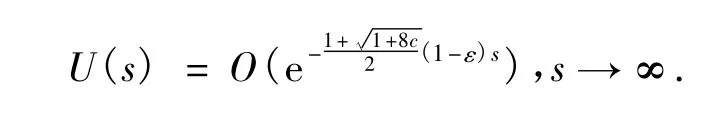
把上式带入(4)式,并注意到在U(s)=0附近,则有:
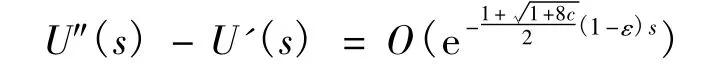
所以有:
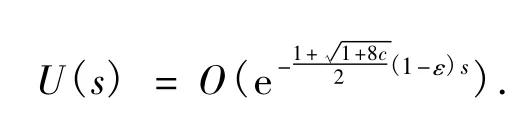
注意到变换s=-t,因此有当t→-∞ 时有:

因r=et,所以当r→0时有:
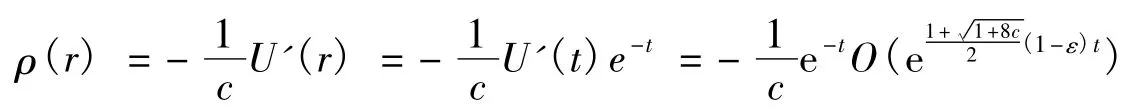
[1]P.A.M.Dirac.The Theory of Magnetic Poles[J].Phys.Rev.74(1948)817.
[2]Y.M.Cho,Kyoungtae Kimm.Electroweak monopoles[J].hep-th/9705213.
[3]Yisong Yang.Solitons in Field Theory and Nonlinear Analysis[M].America:Springer Monographs in mathematics,2001.
Existence and Uniqueness of Electroweak Monopole
ZU Ding-li
(Department of Social Sciences,Mathematics and Physics,Chengde Petroleum College,Chengde 067000,Hebei China)
Electroweak monopole has an important application value in the phenomenology of the electroweak theory.This paper mainly proves the existence and uniqueness of the electroweak monopole by dynamical shooting method,and obtains asymptotic estimates for the solutions at original point.
electroweak monopole;dynamical shooting;existence and uniqueness
O44
B
1008-9446(2013)04-0038-04
河北省高等学校科学研究计划项目(磁单极子的存在性问题):Z2010208
2013-04-16
祖定利(1977-),男,陕西渭南人,承德石油高等专科学校社科与数理部讲师,主要从事高等数学教学和偏方程方面研究工作。

