氢键准则在DMSO 水溶液中应用的评价
张 宁 李维仲 陈 聪 左建国
(大连理工大学,海洋能源利用与节能教育部重点实验室,辽宁大连116024)
1 引言
低温保护技术广泛应用于生物技术、动植物育种工程和生物制药等领域.虽然低温环境可以极大地减缓细胞的新陈代谢过程,但是胞内冰的形成会对细胞产生致命的损伤.低温保护剂可以有效地抑制胞内外冰晶的形成,并保持生物组织和细胞的完整性.长期以来,低温保护剂的保护机理在低温生物领域中一直都是研究的热点.由于受到实验手段所能观测的尺度和精度的限制,对保护剂溶液微观结构以及动力学特性的认识还不足以解释其对细胞的低温保护机理.近年来,随着分子尺度数值模拟方法的飞速发展,对低温保护剂溶液微观特性的研究受到越来越多科研人员的关注.
二甲基亚砜(DMSO)具有许多独特的物理化学性质,如高沸点(189°C)、高偶极矩.1由于这些特性,DMSO广泛地应用于低温保护及医药工业领域.从分子结构上看,DMSO分子中存在两个疏水性的甲基团,但是DMSO与水分子之间仍然具有较强的氢键作用.正是这些氢键的存在才减弱了DMSO水溶液中冰晶形成的相变驱动力.2此外,研究者发现,甲基的存在可以有效地抑制保护剂分子间的相互作用,使其只与水分子发生氢键作用,从而增强了保护剂对溶液中冰晶抑制的效果.因此,DMSO水溶液的氢键结构和动力学性质受到了广大科研者的关注.Soper和Luzar3采用分子动力学方法分析了不同浓度下DMSO水溶液的局部水合结构,包括不同原子间的配对相关函数、水合数以及不同分子对间的氢键结构.Vishnyakov及其合作者4研究了氢键作用在DMSO水溶液中引起的团簇结构,如:DMSO·2H2O和DMSO·3H2O等.Kirchner和Hutter5采用Car-Parrinello分子动力学方法研究了DMSO水溶液的微观结构.Lei等6对不同浓度下的DMSO水溶液的非理想特性进行了研究.研究表明,模拟结果与核磁共振(NMR)结果在变化趋势上相一致.Geerke等7主要从热力学和动力学的角度对DMSO模型进行了研究.Mancera等8,9研究了温度和浓度对DMSO水溶液氢键结构及动力学性质的影响.张霞等10采用两种不同的力场分析了DMSO水溶液中的氢键寿命.最近,Chowdhuri和Pattanayak11针对氢键的结构弛豫时间,模拟了压力对DMSO水溶液的影响.Wong等12利用偏振选择性红外泵探针、二维红外振动回波光谱和光学外差光学克尔效应等实验手段对DMSO水溶液中氢键的动力学特性进行了深入的研究.就目前来看,由于氢键的几何准则简便易行,大多数对于氢键的研究4,13−15都基于此准则;也有少数研究者采用比较复杂的能量准则16,17或混合型准则.18本文利用分子动力学方法研究了不同浓度下DMSO水溶液的氢键结构及其动力学特性,并探求采用不同的氢键准则对分析结果的影响.
2 模拟细节
本文采用NAMD程序19模拟不同浓度下的DMSO水溶液.溶液体系中,DMSO采用Strader和Feller开发的力场,20水模型分别采用SPC/E、21TIP3P22和TIP4P22,23模型.模拟体系选取NPT系综,采用Nosé-Hoover法24使温度和压力分别保持在298 K和101 kPa,并采用Langevin方法控制压力波动.计算体系采用立方周期性边界条件,这在一定程度上可以消除边界影响.应用势能截断法使非键势能从1.0 nm缓慢减小到零,截断半径为1.2 nm.截断距离之外的分子间相互作用采用长程校正法进行校正.对长程静电相互作用力的计算,采用particle mesh Ewald(PME)方法25每2个步长计算一次.模拟过程中选取时间步长为2 fs,每次模拟计算总时间为10 ns,其中前5 ns使体系达到平衡,后5 ns用于统计计算体系的各种性质.本文共模拟了6个DMSO水溶液体系,体系的具体组成参数见表1.
3 氢键结构和动力学分析
3.1 氢键准则
在分析DMSO水溶液的氢键结构和动力学特性时,首先是对氢键进行定义.在分子模拟中,可以得到体系中所有原子在每一瞬时时刻的位置坐标以及原子间的相互作用能.因此,对于氢键的定义通常采用两种方式,即:几何准则和能量准则.未加特殊说明,本文中使用的水模型为SPCE模型.
3.1.1 几何准则
如果两个分子在空间位置上满足一定的约束条件,我们就可以认为这两个分子之间存在氢键作用.这些用来判断两个分子间存在氢键作用的空间约束条件被称为几何准则.研究者通常选择三个距离和三个角度中的两个或三个条件作为判断氢键的几何准则.以氢键O―H…O为例,三个距离约束条件分别为O―H、O…O和O…H键长,其中O―H为共价键长度,它是由所采用的势能模型和计算方法确定的,因此通常选取O…O和O…H作为几何准则中的距离约束条件;14,26三个角度约束条件分别为O―H…O、H―O…O和H…O…O角度,其中,前两者的使用比较广泛.27,28在氢键的几何准则中,距离约束是必不可少的,角度约束所起的限制作用要小于距离约束,通常作为几何准则中的附属约束条件出现在氢键定义中.本文所采用的几何准则包括三个约束条件,即:O…O、O…H键长和H―O…O角度.
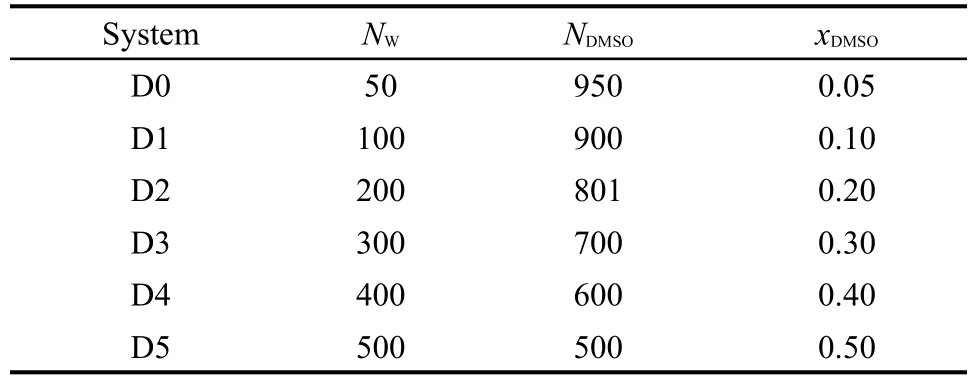
表1 DMSO水溶液体系的参数Table 1 Parameters of DMSO aqueous solutions
由于本文所研究的DMSO分子只作为氢键受体存在于水溶液中,因此对氢键的分析只需考虑两种类型,即:H2O…H2O和DMSO…H2O.在MD模拟中,一般通过计算不同原子对的径向分布函数来确定距离约束条件.图1给出了二元溶液中分子间的O…O和O…H原子对在不同浓度下的径向分布函数,其中OW和OD分别代表水和DMSO分子中的氧原子,HW代表水分子中的氢原子.从图可以看出,在不同浓度下,每种原子对的径向分布函数曲线都发生相似的波动,即:波峰和波谷出现的位置几乎一致.不同的是,波峰和波谷的高度随着浓度的增加而呈现出单调的变化.对于几何准则中距离约束的确定,通常选择径向分布函数的第一个波谷位置作为该对原子间氢键作用的极限距离.OW…OW和OW…OD径向分布函数(图1(a)和1(b))的第一个波谷位置都出现在0.34 nm附近;4OW…HW和OD…Hw径向分布函数(图1(c)和1(d))的第一个波谷位置则都保持在0.25 nm附近.因此,本文将上述的波谷位置作为几何准则中的距离约束条件,并采用统一的标准来定义上述两种氢键类型(H2O…H2O和DMSO…H2O),即

图1 不同浓度下DMSO水溶液中原子对的径向分布函数Fig.1 Radial distribution functions of the atom pairs in the DMSO aqueous solutions of different concentrations

图2 H2O-H2O分子间(a)和DMSO-H2O分子间的α角分布曲线Fig.2 Angle α distribution curves for the H2O-H2O(a)and DMSO-H2O(b)pairs
此外,还需选择合适的角度约束条件来补充定义氢键的几何准则.本文所选择的角度约束条件为H―O…O取向角,此角度广泛地应用在氢键的定义中.图2给出了H2O…H2O和DMSO…H2O氢键的结构示意图.如图所示,α角即为本文所采用的角度约束条件.图2还给出了DMSO水溶液中两种类型分子对(H2O:H2O和DMSO:H2O)所构成的α角分布曲线.图中的α角是由溶液体系中分子间的O…H距离小于0.25 nm的两个分子所构成的夹角.图中α角呈现单峰分布,其最大值出现在10°处.此最大值出现的位置随DMSO浓度的变化几乎不发生改变,但其值却受到浓度的影响.随着DMSO浓度的增加,α角分布的峰值呈现减小的趋势.这一现象在H2O:H2O分子对中表现得较为明显.从图可以看出,α角集中分布在角度较小的区域内;当角度大于60°时,α角分布几乎为零.这说明了O…H距离约束条件在很大程度上剔除了不能构成氢键的分子对.本文还分别统计了两种分子对在α≤30°范围内α角的累积分布:对于H2O:H2O分子对,α角在所关注的浓度范围内的累计分布为93.3%−98.8%,且随浓度的增加而增加;对于DMSO:H2O分子对,α角的累计分布为96.8%−99.5%,其变化趋势与H2O:H2O分子对类似.由此可知,在α≤30°范围内的分子对的数量占到总数量的90%以上.因此,本文将此广泛使用的角度(30°)13,14,29作为角度约束的极限值,即:α≤30°.综上所述,本文所采用的几何氢键准则可表示为ROO≤0.34 nm,ROH≤0.25 nm,α≤30°.
值得注意的是,形成氢键的水分子间的偶极方向夹角的分布不是均匀分布在0°−180°之间的.本文通过上述的氢键准则计算出此夹角集中分布在10°−120°范围内.因为当超出了此范围,分子间的相互作用能会增加,因而氢键结构不稳定.
3.1.2 能量准则
通过分子动力学模拟可以方便地得到体系中的任意类型两分子间的对势能Eij(r),用下式表示:Eij(r)=Uij(r)+Qij(r),式中,Uij(r)和Qij(r)分别为分子i,j间的Lennard-Jones势能和静电势能.通过对势能的计算可以清楚地反映出分子间的相互作用情况以及体系的微观结构.30图3分别给出了不同浓度下的H2O:H2O和DMSO:H2O分子对的对势能分布曲线.从图可以看出,浓度对两种对势能分布影响不大.此外,对于H2O:H2O和DMSO:H2O分子对,其对势能分布曲线都呈现出双峰分布,其中,主峰以Eij(r)=0为中心并向两侧递减,这主要是由相距较远的分子对产生的;另一个峰值出现在势能为负的区域,说明存在某种势能使一定数量的分子对发生相互吸引作用.研究者16,17,30发现,负势能区域的峰值是在氢键的作用下产生的.因此,可通过图3所示的对势能曲线确定氢键的能量准则.本文将对势能分布曲线的波谷位置定义为氢键的能量约束条件,即:对于 H2O:H2O 分子对,Eij(r)≤−12 kJ·mol−1,这与前人的研究结果一致;17,31对于DMSO:H2O分子对,Eij(r)≤−17 kJ·mol−1.

图3 H2O-H2O分子间(a)和DMSO-H2O分子间(b)的对势能分布曲线Fig.3 Distribution curves of pair interaction energy Eijfor the H2O-H2O(a)and DMSO-H2O(b)pairs
3.2 氢键统计
本文分别采用几何准则和能量准则对DMSO水溶液进行氢键统计分析.分析的内容包括每种分子的氢键平均数nHB和参与n个氢键的分子数目百分比分布fn.图4给出了不同浓度下的水分子和DMSO分子的氢键平均数.如图所示,采用几何准则确定的氢键平均数比能量准则所得到的结果稍大,但其差异不超过2%,这与其它的研究结果相似.26水分子的氢键平均数随着浓度的增加而逐渐减小,如图4(a)所示.这是因为DMSO分子不断地取代水分子并抑制了水分子间的氢键作用,进而使水分子作为氢键受体的几率不断降低.水分子的氢键平均数随浓度的变化趋势与前人的研究成果6相一致.而DMSO分子在水溶液中只充当氢键受体,所以随着浓度的增加,DMSO的氢键平均数也呈现减小的趋势,如图4(b)所示.此变化趋势同样与前人成果29一致.在本文所研究的浓度范围内,水分子和DMSO分子的氢键平均数随浓度呈现近似线性的变化.从图4(a)可以看出,DMSO浓度的增加将不断地分解整个水分子的氢键网络.32但是DMSO却保留了水分子的局部氢键结构,如表2所示.
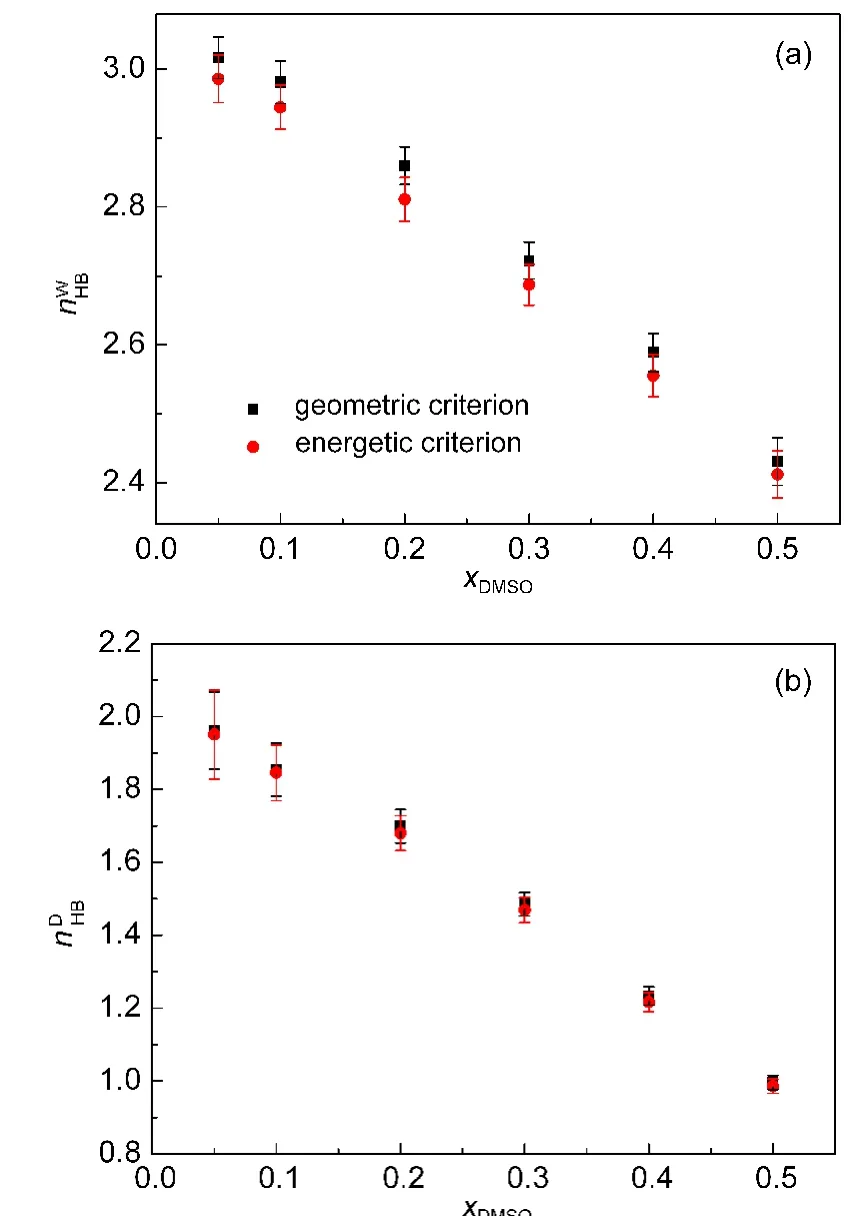
图4 不同浓度下的水分子(a)和DMSO分子(b)的氢键平均数(,Fig.4 Average number(nWHB,nDHB)of hydrogen bonds for water(a)and DMSO(b)molecules for different concentrations
表2给出了不同浓度下具有n个氢键的水分子和DMSO分子的数目百分比,其中氢键的统计分别采用几何准则和能量准则.表中的氢键分布趋势与其它模拟结果非常相似.33在不同浓度的体系中,参与3个氢键的水分子一直占有很大的比重.这在一定程度上说明了DMSO起到了保护水分子局部氢键结构的作用.34但是参与4个氢键的水分子却随着浓度的增加而减少.这同样预示着DMSO通过替代水分子进而不断地分解着水分子间形成的氢键网络.此外,具有两个氢键的DMSO分子占大多数,并且随着浓度的变化呈现出非单调的变化趋势.值得指出的是,几何准则和能量准则在氢键统计上的效果存在一些差异.
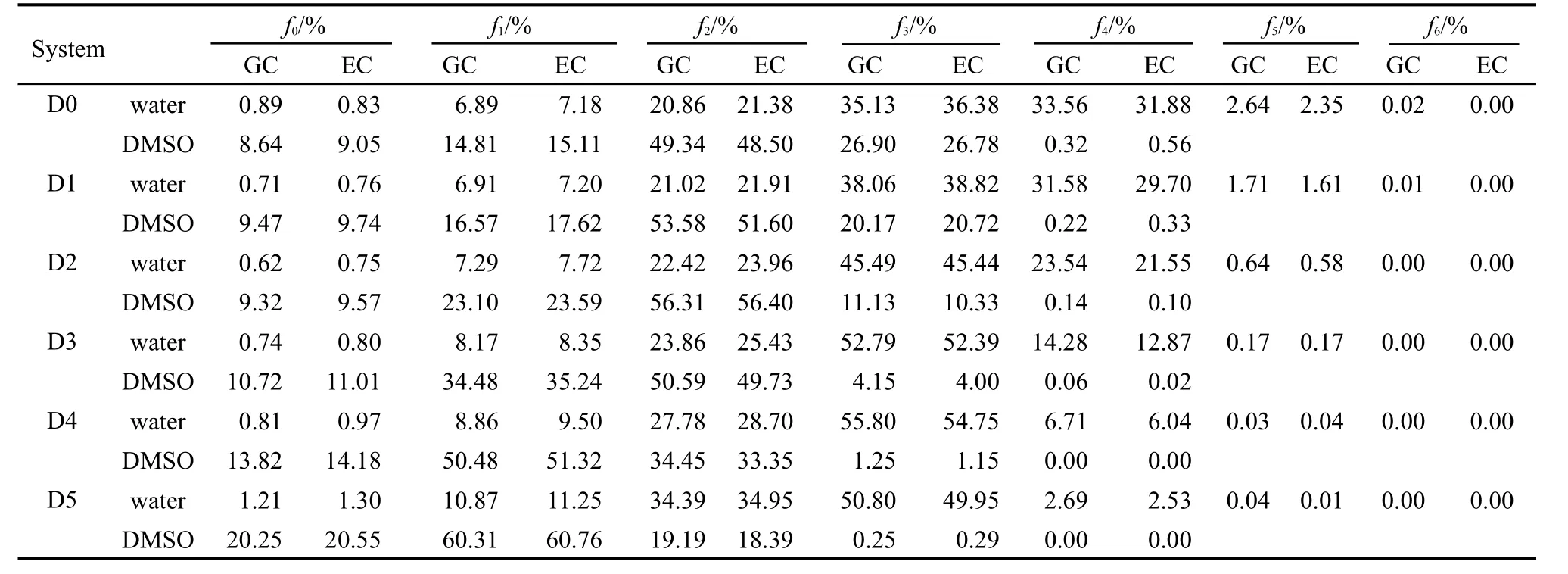
表2 不同体系下参与i个氢键的水和DMSO分子数目的平均百分比(fi)Table 2 Average fraction(fi)of the water and DMSO with i hydrogen bonds for different systems
本文还将TIP3P和TIP4P水模型应用D2体系中,并计算出两种体系下的水分子和DMSO分子的氢键平均数,如图5所示.为便于比较,图中还给出了图4中的D2体系的结果.与SPCE水溶液的结果相似,采用几何准则统计出的氢键平均数稍大于由能量准则产生的结果.
3.3 氢键动力学分析
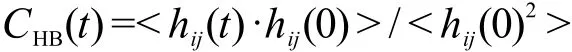
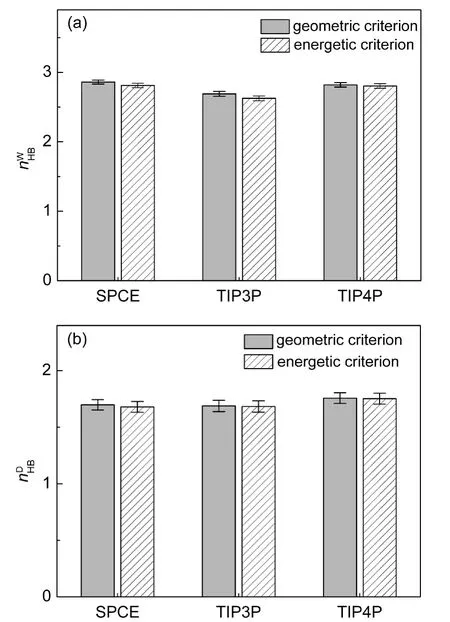
图5 SPCE,TIP3P和TIP4P水模型在D2体系中的水分子(a)和DMSO分子(b)的氢键平均数Fig.5 Average number of hydrogen bonds per water(a)and DMSO(b)for SPCE,TIP3P,and TIP4P models in D2 system
由于分子的振动和平动,平衡体系中分子间的氢键会发生不断的断裂和重建.为了分析这一动力学特性,人们提出了氢键寿命的概念.35研究者们通常使用自相关函数,CHB(t),来描述氢键的动力学特性,35−37其表达式如下:其中,i,j(i≠j)代表体系中不同的分子对.如果某分子对i j在0和t时刻都存在氢键作用,并且此氢键在此时间段内从未发生断裂,则hij(t)=1;否则,hij(t)=0.根据此连续自相关函数的计算结果,采用Elola等36提出的方法,本文通过如下公式计算氢键寿命(τ):

由于氢键寿命的计算是以氢键的存在为基础,因此氢键准则在计算氢键寿命的过程中是十分重要的.本文采用氢键的几何准则和能量准则分别计算H2O…H2O和DMSO…H2O的氢键寿命,如表3所示.通过能量准则确定的氢键寿命总体上大于几何准则的结果.这种差异在DMSO…H2O的氢键寿命上表现得比较明显,最大的相对误差为16.5%(D1).此外,每个体系中的DMSO…H2O的氢键寿命τWD大于H2O…H2O的氢键寿命τWW.这与Vishnyakov等4的研究成果相一致.这说明了DMSO与水分子间的氢键作用更加紧密,同时也验证了DMSO可以强化与之相连的水分子的氢键结构.38此外,本文还统计了TIP3P和TIP4P水模型在D2体系中的氢键寿命τWW和τWD,如表4所示.为了方便对比,表中还给出了表3中D2体系的结果.结果显示,对于三种不同的水模型,氢键的几何准则和能量准则产生的影响是相似的,即:采用能量准则确定的氢键寿命大于几何准则的结果.
3.4 氢键准则评估
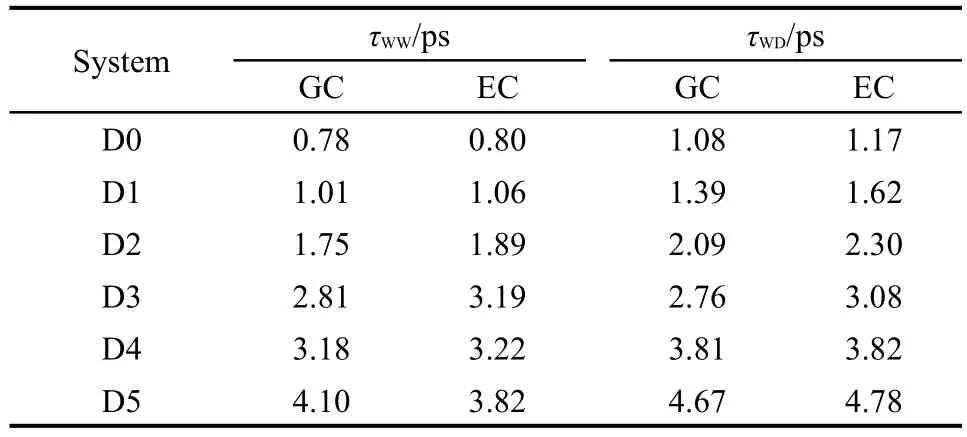
表3 氢键寿命的计算结果Table 3 Results of hydrogen bonding lifetime
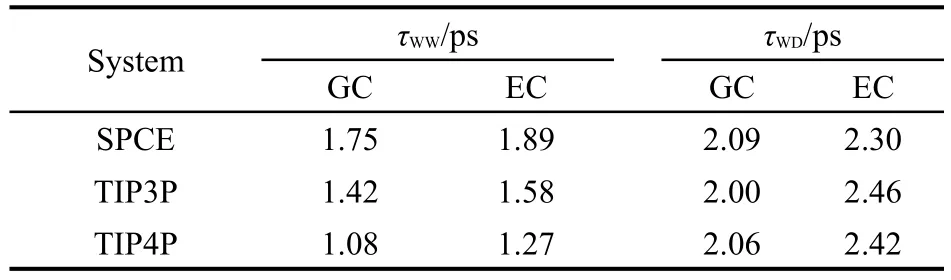
表4 SPCE,TIP3P和TIP4P水模型在D2体系中的氢键寿命Table 4 Hydrogen bonding lifetime for SPCE,TIP3P,and TIP4Pwater models in D2 system
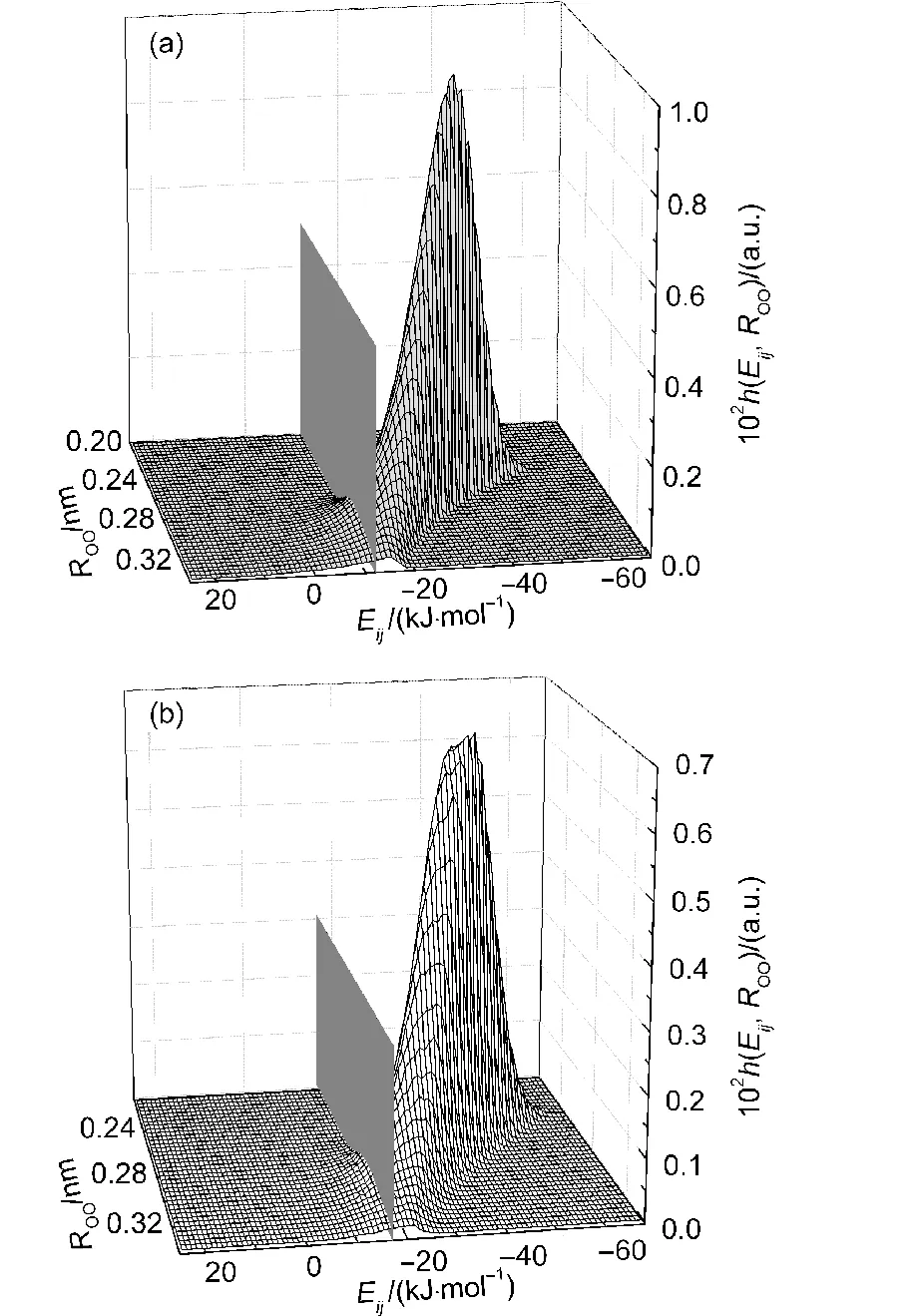
图6 在浓度为xDMSO=0.20的DMSO水溶液中采用几何准则确定的氢键中的H2O-H2O分子间(a)和DMSO-H2O分子间(b)的O…O距离−对势能分布图Fig.6 Distribution of intermolecular O…O distance−pair interaction energy for the hydrogen bonded H2O-H2O(a)and DMSO-H2O(b)pairs which are determined by geometric criterion in the DMSO aqueous solution of xDMSO=0.20
对于氢键统计,几何准则的统计结果稍稍大于能量准则的结果,但两者相差不大;对于氢键动力学分析,采用能量准则计算得到的氢键寿命普遍大于几何准则的结果.这反映出两种氢键准则在判断氢键的细节上存在不足.为了说明这种不足,本文分别计算了由几何准则确定的氢键的对势能分布和由能量准则确定的氢键的ROO距离分布和α角分布.
如图6所示,采用几何准则统计得到的氢键大都分布在对势能为负的区域,并且集中分布在−30 kJ·mol−1附近.从图可以看出,采用几何准则确定的氢键基本上满足了能量准则的要求.值得注意的是,仍有少数氢键出现在能量准则规定的条件之外.对于氢键H2O…H2O,存在5.0%的氢键出现在大于−12 kJ·mol−1的对势能区域内;对于氢键DMSO…H2O,则有数量为2.9%的氢键出现在大于−17 kJ·mol−1的对势能区域内.由此可知,采用几何准则计算得到的结果会包含少量不合理的氢键(即:对势能偏高的分子对),这将对氢键的定量分析产生影响.
图7给出了采用能量准则得到的氢键的ROO距离分布.如图所示,由能量准则确定的氢键中,只有少量氢键不满足几何准则中的距离约束条件ROO.在氢键H2O…H2O和DMSO…H2O中,分别存在0.6%和0.4%超出了距离约束条件.此外,本文还考查了能量准则确定的氢键的α角分布,如图8所示.两种氢键的α角绝大部分都满足几何准则的角度约束条件,仅有很少一部分的α角大于30°.能量准则只针对两分子间的对势能进行评判,对于分子间的相对转动未加限制.在计算氢键寿命时,如果两分子只发生微小的相对转动并且分子间的对势能满足能量准则,那么这两个分子仍然被判定具有氢键作用.因此,采用能量准则计算得到的氢键寿命要大于几何准则的结果.此外,氢键DMSO…H2O的α角超出角度约束条件的比例大于氢键H2O…H2O,其中,DMSO…H2O为7.1%,H2O…H2O为4.2%.因而,由能量准则得到的DMSO…H2O氢键寿命与几何准则的结果相比偏差较大.
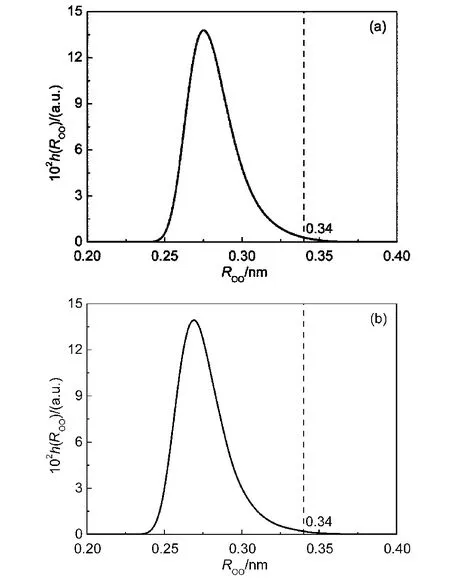
图7 在浓度为xDMSO=0.10的DMSO水溶液中采用能量准则确定的氢键中的H2O-H2O分子间(a)和DMSOH2O分子间(b)的O…O距离分布曲线Fig.7 Distribution curves of intermolecular O…O distance for the hydrogen bonded H2O-H2O(a)and DMSOH2O(b)pairs which are determined by energetic criterion in the DMSO aqueous solution of xDMSO=0.10
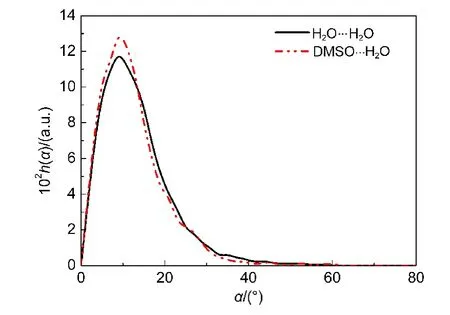
图8 在浓度为xDMSO=0.10的DMSO水溶液中采用能量准则确定的氢键中的H2O-H2O分子间和DMSO-H2O分子间的α角分布曲线Fig.8 Distribution curves of intermolecular angle α for the hydrogen bonded H2O-H2O and DMSO-H2O pairs which are determined by energetic criterion in the DMSO aqueous solution of xDMSO=0.10
4 结论
利用分子动力学方法研究了不同浓度的DMSO水溶液的氢键统计和动力学特性.此外,分别采用几何准则和能量准则判定氢键的存在,并分析两种氢键准则的合理性.本文通过氢键统计计算三种水模型(SPCE、TIP3P和TIP4P)下的溶液体系,发现几何准则确定的氢键数略大于能量准则的结果,且采用两种准则得到的氢键数随浓度的变化趋势保持一致.由能量准则计算得到的氢键寿命大于几何准则的结果,并且此差异在氢键DMSO…H2O中表现得比较明显.这说明几何准则对氢键的动力学限制更严格.采用两种氢键准则都反映出氢键寿命随DMSO浓度的增加而增大.通过分析发现,采用几何准则得到的结果中不合理的氢键比例大于通过能量准则得到的结果,这说明能量准则能够比较准确地判断出氢键的存在;此外,能量准则的不合理性又导致计算得到的氢键寿命偏大.当计算能力满足要求时,采用几何-能量混合型氢键准则可以更加精确地进行氢键结构和动力学的分析.
(1) Lide,D.R.CRC Handbook of Chemistry and Physics,85th ed.;CRC Press:Boca Raton,FL,2005.
(2) Hu,T.J.;Zhou,G.Y.;Gao,C.;Hua,Z.Z.Chin.J.Chem.Phys.2005,18(5),845.[胡桐记,周国燕,高 才,华泽钊.化学物理学报,2005,18(5),845.]
(3) Soper,A.;Luzar,A.J.Chem.Phys.1992,97(2),1320.doi:10.1063/1.463259
(4) Vishnyakov,A.;Lyubartsev,A.P.;Laaksonen,A.J.Phys.Chem.A 2001,105(10),1702.doi:10.1021/jp0007336
(5) Kirchner,B.;Hutter,J.Chem.Phys.Lett.2002,364(5−6),497.doi:10.1016/S0009-2614(02)01377-5
(6) Lei,Y.;Li,H.;Han,S.Chem.Phys.Lett.2003,380(5−6),542.doi:10.1016/j.cplett.2003.09.064
(7) Geerke,D.P.;Oostenbrink,C.;van der Vegt,N.F.A.;van Gunsteren,W.F.J.Phys.Chem.B 2004,108(4),1436.doi:10.1021/jp035034i
(8) Mancera,R.L.;Chalaris,M.;Refson,K.;Samios,J.Phys.Chem.Chem.Phys.2004,6(1),94.doi:10.1039/b308989d
(9) Mancera,R.L.;Chalaris,M.;Samios,J.J.Mol.Liq.2004,110(1−3),147.doi:10.1016/j.molliq.2003.09.010
(10) Zhang,X.;Zhang,Q.;Zhao,D.X.Acta Phys.-Chim.Sin.2011,27(11),2547.[张 霞,张 强,赵东霞.物理化学学报,2011,27(11),2547.]doi:10.3866/PKU.WHXB20111107
(11) Chowdhuri,S.;Pattanayak,S.K.Mol.Phys.2012,111(1),135.
(12)Wong,D.B.;Sokolowsky,K.P.;El-Barghouthi,M.I.;Fenn,E.E.;Giammanco,C.H.;Sturlaugson,A.L.;Fayer,M.D.J.Phys.Chem.B 2012,116(18),5479.doi:10.1021/jp301967e
(13) Chen,C.;Li,W.Z.Acta Phys.-Chim.Sin.2009,25(3),507.[陈 聪,李维仲.物理化学学报,2009,25(3),507.]doi:10.3866/PKU.WHXB20090318
(14)Chen,C.;Li,W.Z.;Song,Y.C.;Weng,L.D.Acta Phys.-Chim.Sin.2011,27(6),1372.[陈 聪,李维仲,宋永臣,翁林岽.物理化学学报,2011,27(6),1372.]doi:10.3866/PKU.WHXB20110626
(15) Zhang,N.;Li,W.;Chen,C.;Zuo,J.;Weng,L.Mol.Phys.2013,111(7),939.doi:10.1080/00268976.2012.760050
(16) Stillinger,F.H.;Rahman,A.J.Chem.Phys.1972,57(3),1281.doi:10.1063/1.1678388
(17) Bako,I.;Megyes,T.;Balint,S.;Chihaia,V.;Bellissent-Funel,M.C.;Krienke,H.;Kopf,A.;Suh,S.H.J.Chem.Phys.2010,132(1),014506.doi:10.1063/1.3268626
(18) Swiatla-Wojcik,D.Chem.Phys.2007,342(1−3),260.doi:10.1016/j.chemphys.2007.10.009
(19) Phillips,J.C.;Braun,R.;Wang,W.;Gumbart,J.;Tajkhorshid,E.;Villa,E.;Chipot,C.;Skeel,R.D.;Kalé,L.;Schulten,K.J.Comput.Chem.2005,26(16),1781.
(20) Strader,M.L.;Feller,S.E.J.Phys.Chem.A 2002,106(6),1074.doi:10.1021/jp013658n
(21) Berendsen,H.J.C.;Grigera,J.R.;Straatsma,T.P.J.Phys.Chem.1987,91(24),6269.doi:10.1021/j100308a038
(22) Jorgensen,W.L.;Chandrasekhar,J.;Madura,J.D.;Impey,R.W.;Klein,M.L.J.Chem.Phys.1983,79(2),926.doi:10.1063/1.445869
(23) Jorgensen,W.L.;Madura,J.D.Mol.Phys.1985,56(6),1381.doi:10.1080/00268978500103111
(24) Martyna,G.J.;Tobias,D.J.;Klein,M.L.J.Chem.Phys.1994,101(5),4177.doi:10.1063/1.467468
(25) Darden,T.;York,D.;Pedersen,L.J.Chem.Phys.1993,98(12),10089.doi:10.1063/1.464397
(26) Chowdhuri,S.;Chandra,A.Phys.Rev.E 2002,66(4),041203.doi:10.1103/PhysRevE.66.041203
(27) Guardia,E.;Marti,J.;Padro,J.A.;Saiz,L.;Komolkin,A.V.J.Mol.Liq.2002,96−97,3.
(28) Chelli,R.;Procacci,P.;Cardini,G.;Califano,S.Phys.Chem.Chem.Phys.1999,1(5),879.doi:10.1039/a808957d
(29) Luzar,A.;Chandler,D.J.Chem.Phys.1993,98(10),8160.doi:10.1063/1.464521
(30) Kalinichev,A.G.;Gorbaty,Y.E.;Okhulkov,A.V.J.Mol.Liq.1999,82(1−2),57.doi:10.1016/S0167-7322(99)00042-2
(31) Meng,E.C.;Kollman,P.A.J.Phys.Chem.1996,100(27),11460.doi:10.1021/jp9536209
(32) Towey,J.J.;Soper,A.K.;Dougan,L.J.Phys.Chem.B 2012,116(47),13898.doi:10.1021/jp3093034
(33) Borin,I.A.;Skaf,M.S.J.Chem.Phys.1999,110(13),6412.doi:10.1063/1.478544
(34) Vaisman,I.I.;Berkowitz,M.L.J.Am.Chem.Soc.1992,114(20),7889.doi:10.1021/ja00046a038
(35) Rapaport,D.C.Mol.Phys.1983,50(5),1151.doi:10.1080/00268978300102931
(36) Elola,M.D.;Ladanyi,B.M.J.Chem.Phys.2006,125(18),184506.doi:10.1063/1.2364896
(37) Skarmoutsos,I.;Guardia,E.;Samios,J.J.Chem.Phys.2010,133(1),014504.doi:10.1063/1.3449142
(38) Soper,A.K.;Luzar,A.J.Phys.Chem.1996,100(4),1357.doi:10.1021/jp951783r
——《势能》

