卫星出/入境期的钟差参数两步法拟合算法*

杜 兰 林 丽 王若璞 朱凌凤 刘 利

1)信息工程大学导航与空天目标工程学院，郑州 450052

2)第二炮兵装备研究院，北京 100085

3)北京环球信息应用开发中心，北京 100094

卫星出/入境期的钟差参数两步法拟合算法*

杜 兰1)林 丽2)王若璞1)朱凌凤3)刘 利3)

1)信息工程大学导航与空天目标工程学院，郑州 450052

2)第二炮兵装备研究院，北京 100085

3)北京环球信息应用开发中心，北京 100094

卫星出境数小时后的入境钟差预报参数，是基于24小时历史数据拟合的二次项系数。在传统导航钟参数拟合算法的基础上，根据卫星钟的频偏和频漂参数在不同拟合时段的变化特性，分别选取最佳拟合时段，提出长短期数据结合的两步法拟合算法。基于实测数据的拟合预报实验表明，两步法的预报效果优于直接法。

导航卫星;钟差预报;钟偏;频偏;频漂

1 引言

卫星导航用户在高精度定位时，需要用卫星发播的星历参数和钟差改正参数计算其时空基准［1－3］。其中，星历参数是基于外推的精密轨道拟合得到的，其拟合算法仅对数学意义上的拟合精度有要求［1］;但是钟参数的拟合数据是卫星钟差的历史序列，并将拟合参数直接用于外推时段的钟差改正［4］，因此，为保证钟差预报精度，还要求拟合参数尽可能符合钟运行的物理特性。

受制于目前星载原子钟的稳定性能，我国导航卫星的钟参数计算以2小时数据的线性拟合为主，并采取每小时快速更新策略。但是区域布站致使IGSO和MEO卫星有频繁的持续数小时的境外段;此外，三类卫星在星载原子钟的设备调试或故障情况下，也会出现数小时的数据缺失或不可用。此时，为保证入境或恢复服务后钟参数的正常发播，需要借助中长期历史数据。通常是采用中断前的24小时数据拟合得到二次多项式系数，经过历元归算作为恢复后的预报钟偏、频偏和频漂。

事实上，钟的特性参数在不同时段有各自的变化特性，因而反算钟参数应根据钟的特性选取各自的最佳拟合时段。本文基于实测钟差数据首先分析了拟合频偏和频漂关于拟合时段的变化特征，进而提出长短期历史数据相结合的两步法拟合算法。与传统一步法相比，两步法顾及了拟合频偏的短期局部波动改正，可以明显改善预报精度。

2 预报钟差及其误差分析

二次多项式是星载原子钟的通用预报模型之一。其预报钟差的误差主要源于预报时段内钟偏、频偏和频漂参数(a0，a1，a2)与拟合钟参数(0，1，2)的不一致及其时间累积［5－7］。即

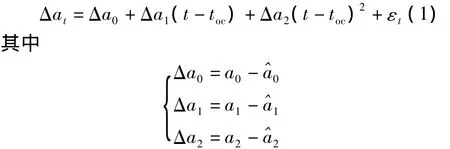
式中，toc是预报段的历元时刻，εt表示钟差的模型误差累积和随机误差之和，对于常规的2小时短期预报，εt的影响可以忽略。

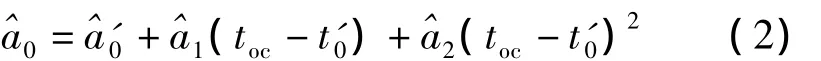
式中t'0和0为拟合段的历元时刻和拟合钟偏。

因此，在忽略拟合误差的情况下，这种一步法预报的钟差误差主要由拟合频偏和频漂的不符值和中断时数决定。

需要指出的是，采用一步法进行高精度预报有一个前提，即中断前后的数小时内，频偏和频漂应具有一致的稳定性。若星载钟在数小时内频偏或频漂波动较大，则将影响到拟合参数对中断恢复后的预报能力。

3 拟合频偏/频漂的稳定性

针对我国导航卫星的星载钟，选取全天可视的GEO卫星进行拟合参数的稳定性分析。

数据源为GEO导航卫星上的某型号铷钟经星地时间比对得到的实时卫星钟差数据，标称精度为0.1 ns，数据总长度3 天，采样率1 s，分别采用1 ～48小时窗口拟合二次项模型，且每小时向后滑动窗口，统计出拟合频偏和频漂与拟合窗口大小的关系(图1)。

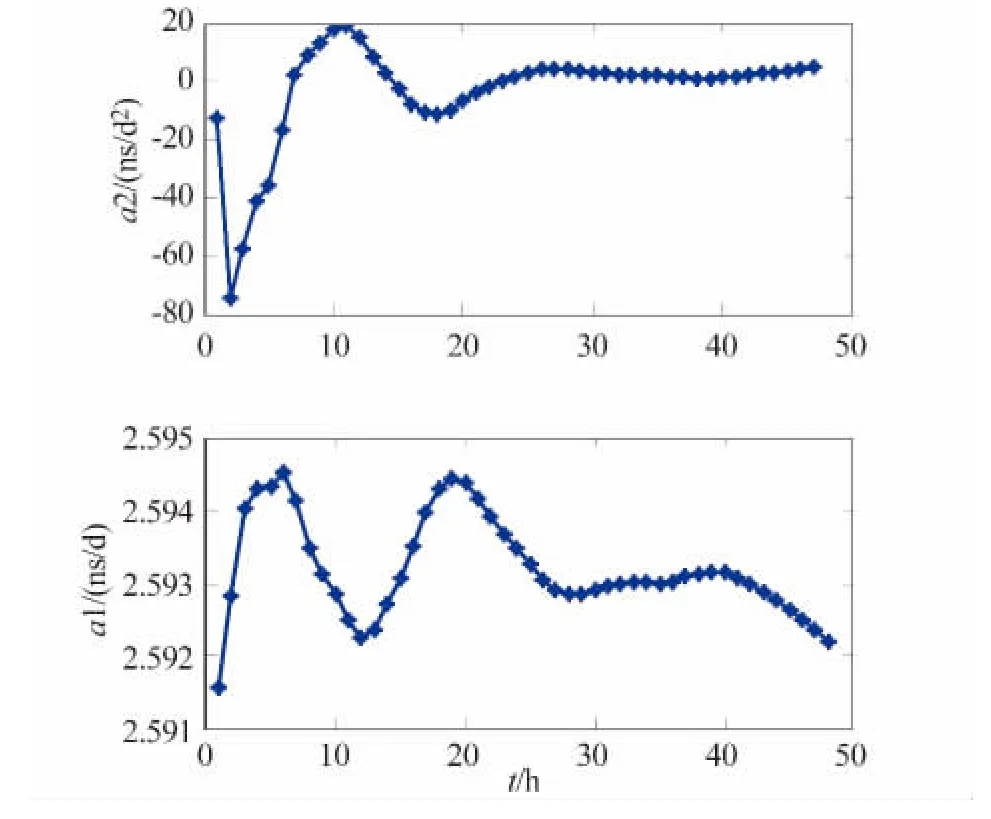
图1 a2和a1拟合值与拟合时段的关系(1～48小时)Fig.1 Fitted a1 and a2 v.s.length of fitting arcs(1 ～48 h)

1)频偏和频漂拟合值的稳定性与拟合窗口的大小有关，表现为低于24小时时段数据的拟合结果不稳定，波动幅度大，从24小时附近开始趋于稳定，超过40小时后频偏拟合值出现递减现象。

3)当拟合时段小于1天时，拟合结果与钟特性参数关联性开始变差，甚至无关联。如2小时短期数据的拟合值变化幅度显著，违背了正常原子钟的物理特性，表明二次多项式拟合结果仅能表现数据段内数学最佳拟合，不能进行钟差预报。

另一方面，短期数据的线性拟合能够反映频偏的波动性。图2为3天共计71组的2小时线性拟合得到的频偏相对变化序列，除有整体增加的趋势外，每小时更新值的变化幅度显著，最大达到20 ns/d。如从第50组开始的5小时内频偏累积变化约60 ns/d，则5小时后能引起最大12 ns的预报偏差。注意到这种短期波动，在1天窗口的二次多项式拟合中则被平滑滤去(图1(b))。

图2 2小时线性拟合的a1拟合值相对变化序列Fig.2 a1 series of 2 h linear fit

综上所述，在拟合算法上，应当充分利用钟特性参数及其在不同数据时段上的表现，而非平等对待频偏和频漂参数的拟合窗口。

4 长短期结合的两步法拟合

在传统一步法基础上，顾及频偏的局部波动性，提出两步法拟合算法，通过局部短期数据的线性拟合改善频偏的估计精度。具体计算步骤如下:

1)利用中断前24小时历史数据进行二次多项式拟合，得到频漂拟合值2;

3)对频漂改正后的2小时数据进行线性拟合，得到钟偏和频偏拟合值(0，1);

4)由式(2)将拟合钟偏0归算至预报起始时刻toc，得到归算后的钟偏0;

5 实测数据实验分析

采用数据的说明见第3部分，拟合-预报窗口取为31小时，其中前24小时为拟合窗口，中间人为中断5小时，最后2小时用于恢复后的短期预报。采用以下两种拟合算法进行对比分析:1)24小时数据拟合二次多项式的常规一步法;2)长短期数据结合的两步法，其中短期数据分别采用最近的0.5、1和2小时三种方案。

每小时更新一组窗口，共计算40组。采用预报时段内预报钟差与实测钟差的不符值的最大值作为评价指标。

5.1 常规方法结果

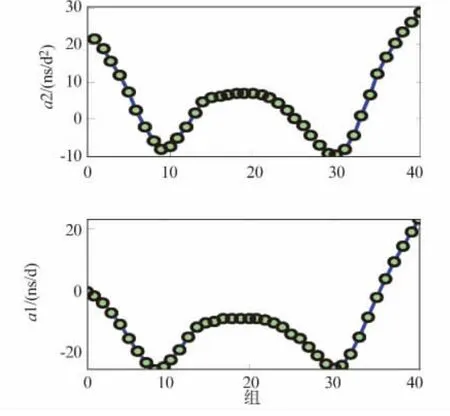
图3 24小时拟合的a2和a1时序变化Fig.3 a2 and a1 series of 24 h quadratic fit

图4 常规方法的钟差预报最大偏差Fig.4 Maximum difference of predicted and observed clock offsets using conventional fit

通过图3和图4可以看出:

1)频漂和频偏的拟合序列存在一定的波动性，频漂有40 ns/d2的变化幅度，并且一致地反映在频偏拟合时序中，只有中间的10组频漂和频偏拟合值相对平稳。这里需要指出的是，由于数据窗口个数有限，不能全面反映我国导航星载钟的水平，但在一定程度上表明星载钟性能有待改善。

2)中断5小时后恢复正常的2小时短期预报，预报精度与数小时内频偏和频漂的波动趋势有一致的因果关系。由图3可以发现，第10和30组为频偏和频漂的趋势性变化较快的两个拐点，对于滞后数小时的预报必然带来大的偏差，图4中相应的预报误差分别达到6 ns和15 ns;对于拟合频漂和频偏相对平稳的中间段，预报钟差的最大偏差均能控制在5 ns以内且变化相对平稳。

5.2 两步法结果

两步法的三种方案，结果相差不大，因此只给出(24+2)小时长短期结合的预报钟差最大不符值时序(图5)。常规一步法和两步法的预报精度的统计对比如图6和表1所示。

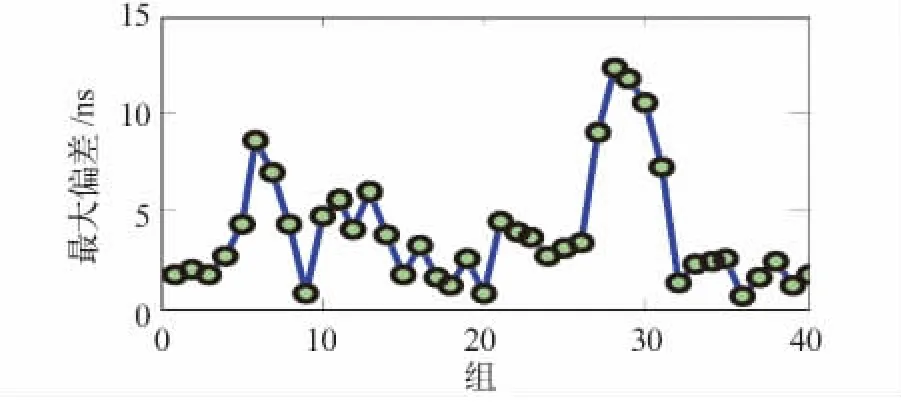
图5 两步法的预报钟差最大偏差Fig.5 Maximum difference of predicted and observed clock offsets using two-step fit

由图5、6和表1可以看出:

1)改进的两步法优于常规方法。从预报优于5 ns的分布统计上看，两步法的个数更多更集中，从一步法的62.5%提高到77.5%，表明就近2小时的线性拟合对拟合频偏具有修正作用。

2)短期频偏修正的拟合时段以1～2小时为最佳。表1的对比表明，相对于2、3和5ns预报精度要求，1～2小时数据对钟模型的线性部分的改善程度均略优于0.5小时。

图6 预报钟差最大偏差的分布Fig.6 Distribution of maximum difference of predicted and observed clock offsets

表1 预报钟差最大偏差的统计Tab.1 Statistics of maximum difference.of predicted and observed clock offsets

3)两步法对于第30组的拐点附近的预报精度未见明显改善(图5)，表明短期数据仅能对拟合频偏进行局部修正，无法适应钟的快速趋势变化。但也提供了一个启示，若能够从长期历史数据中预测出钟特性参数的变化趋势，将有利于探讨短中长三类数据相结合的拟合-预报方法。

6 结语

拟合-预报时段内钟参数的平稳一致性决定了钟差预报的精度。在中断的数小时前后，卫星钟参数的拟合-预报偏差越小，钟差预报精度越高。

对于数小时中断后的钟差预报，直接采用24小时数据的二次多项式拟合，拟合频偏不能反映钟的频偏局部波动。在直接法基础上，利用最近1～2小时短期数据的线性拟合结果能够在一定程度上逼近相邻数小时的频偏变化，实测数据的处理结果表明了这种改进的两步法能够改善钟差预报精度。

无论是直接法还是改进的两步法，其导航钟差预报模式都是直接采用历史数据的拟合结果进行预报。若钟参数的稳定性较差，拟合结果将无法保证预报精度。因此，除不断提高星钟稳定性能外，还应改进钟差的精密预报模型，如引进灰色模型、ARMA模型等，并在精密预报钟差序列的基础上进行钟参数拟合，从而实现与星历参数生成相一致的先预报再拟合的统一模式。

1 何峰，等.地球静止轨道卫星广播星历参数拟合与试验分析［J］.测绘学报，2011，40(增刊):52－58.(He Feng，et al.Ephemeris fitting and experiments analysis of GEO satellite［J］.Acta Geodaetica et Cartographica Sinica，2011，40(Supp.):52 －58)

2 王继刚，等.组合模型预报导航卫星钟差［J］.大地测量与地球动力学，2012，(1):84 － 88.(Wang Jigang，et al.Combination models for navigation satellite clock prediction［J］.Journal of Geodesy and Geodynamics，2012，(1):84－88)

3 黄观文，等.GPS卫星钟差的估计与预报研究［J］.大地测量与地球动力学，2009，(6):118－122.(Huang Guanwen，et al.Research on estimation and prediction of GPS satellite clock error［J］.Journal of Geodesy and Geodynamics，2009，(6):118－122)

4 朱陵凤，等.基于国产氢原子钟的钟差预报方法研究［J］.大地测量与地球动力学，2009，(1):148－151.(Zhu Lingfeng，et al.Research on methods for predicting clock error based on domestic hydrogen atomic clock［J］.Journal of Geodesy and Geodynamics，2009，29(1):148－151)

5 郑作亚，卢秀山，阳凡林.基于IGS超快星历的GPS钟差线性预报分析［J］.测绘科学，2009，34(6):48－50.(Zheng Zuoya，Lu Xiushan and Yang Fanlin.Analysis on GPS satellite clock error linear prediction from IGS ultra-rapid products［J］.Science of Surveying and Mapping，2010，35(2):48－50)

6 郑作亚，等.基于IGS超快星历预报卫星钟差及其精度分析［J］.测绘科学，2010，35(2):8 －12.(Zheng Zuoya，et al.Study on GPS satellite clock bias prediction with IGS ultra-rapid ephemeris［J］.Science of Surveying and Mapping，2010，35(2):8 －12)

7 黄观文，杨元喜，张勤.开窗分类因子抗差自适应序贯平差用于卫星钟差参数估计与预报［J］.测绘学报，2011，40(1):15 － 21.(Huang Guanwen，Yang Yuani and Zhang Qin.Estimate and Predict satellite clock error used adaptively robust sequential adjustment with classified adaptive factors based on opening windows［J］.Acta Geodaetica et Cartographica Sinic，2011，40(1):15－21)

SATELLITE CLOCK PARAMETER TWO-STEP FIT ALGORITHM FOR PERIOD OF OUT-OF-VIEW

Du Lan1)，Lin Li2)，Wang Ruopu1)，Zhu Lingfeng3)and Liu Li3)
1)College of Navigation＆Aerospace Engineering，Information Engineering University，Zhengzhou450052
2)The Equipment Research Institute of the Second Missile Army，Beijing100085
3)Beijing Global Information Application and Development Center，Beijing100094

Quadratic model is fitted with the nearest history data of 24 hours when the satellite is out-of-view，and is used to predict clock offset as soon as the satellite is in view.Based on the conventional fit algorithm，the best fit arcs are selected independently for the two fitting parameters of frequency bias and frequency drift according to their respective characteristics at different length of fitting arcs.A two-step fit is proposed using both long-and short-term data sets.The fit and prediction comparisons using the real clock offset data show that the prediction performance of two-step fit is better overall than the conventional method.

navigation satellite;clock offset prediction;clock bias;frequency bias;frequency drift

P207

A

1671-5942(2013)05-0120-04

2012-09-26

国家自然科学基金(41174025，41174026)

杜兰，教授，博士，主要从事空间大地测量及其数据处理.E－mail:Lan.du09@gmail.com