基于拉普拉斯级数展开法的固体潮波类理论值计算*
苏 融 李胜乐
(中国地震局地震研究所(地震大地测量重点实验室),武汉 430071)
基于拉普拉斯级数展开法的固体潮波类理论值计算*
苏 融 李胜乐
(中国地震局地震研究所(地震大地测量重点实验室),武汉 430071)
基于拉普拉斯级数展开法给出了倾斜固体潮、重力固体潮、应变固体潮的长周期波、日波、半日波、三分之一日波等四种类型的潮波的适合计算机编程实现的理论值计算公式和步骤。用C#程序语言编程实现理论值计算,并编译成动态链接库,可以实现跨平台跨操作系统调用。
固体潮;固体潮波类理论值;拉普拉斯级数展开法;起潮力位;C#
1 引言
地球整体在月亮和太阳作用下的变形称为固体潮。对于给定的地球模型,可以从理论上计算出固体潮理论值,将其与固体潮观测值对比,藉以研究地球内部结构。潮汐波按周期可分为长周期波、日波、半日波、三分之一日波等,研究各波类理论值对了解各波类的变化和固体潮的调制现象都有重要意义。郗钦文[1]给出了地球上重力与地倾斜理论值计算的直接而严密的公式。刘序俨[2]给出了倾斜固体潮长周期波、全日波、半日波和1/3日波的理论值计算公式。本文基于已有的固体潮理论值相关公式,对重力固体潮、应变固体潮各波类理论值公式进行了推导。并给出基于拉普拉斯级数展开法固体潮各波类的计算公式及计算步骤,计算结果可满足现阶段地震台站前兆观测的精度要求。
2 固体潮波类理论值的计算公式
2.1 固体潮波类起潮力位级数展开式
在目前的地震台站前兆观测精度条件下,一般将月亮的起潮位只取至三阶项,太阳的只取至二阶项,则起潮力位的表达式为:

式中,Pn(cosθ)为n阶勒让德多项式,G为万有引力系数,M、S分别为月亮、太阳的质量,m、s分别为月亮、太阳的相关参数[3]。
若先仅考虑式(1)的二阶项W2m、W2s,三阶项W3m,把天顶距展开为赤纬和地方时角的函数,则可得4种球谐潮波[2]。将起潮力位中的各波类的起潮力位分别相加,并令V0、V1、V2、V3分别代表日月起潮力位的长周期波、全日波、半日波和1/3日波[2],则


2.2 固体潮理论值公式
倾斜固体潮长周期波、全日波、半日波毕和1/3日波的理论值计算公式见文献[2]。
2.2.1 重力固体潮理论值计算公式
各波类的理论值的计算式根据文献[3-5]为:

式中的负号表示重力方向指向地心。将式(2)~(5)代入式(6),得δgi的计算公式为:

2.2.2 应变固体潮理论值计算公式
2.2.2.1 面应变固体潮理论值计算公式
由正南北、正东西两个方向的线伸缩观测值计算平面应变的公式为[3]

取 G-A 地球模型的勒夫数[6,7]:h2=0.611 4,h3=0.291 3,L2=0.083 2,L3=0.014 5,将式(2)至(5)代入式(11),得面应变固体潮各波类理论值EAi的公式为:
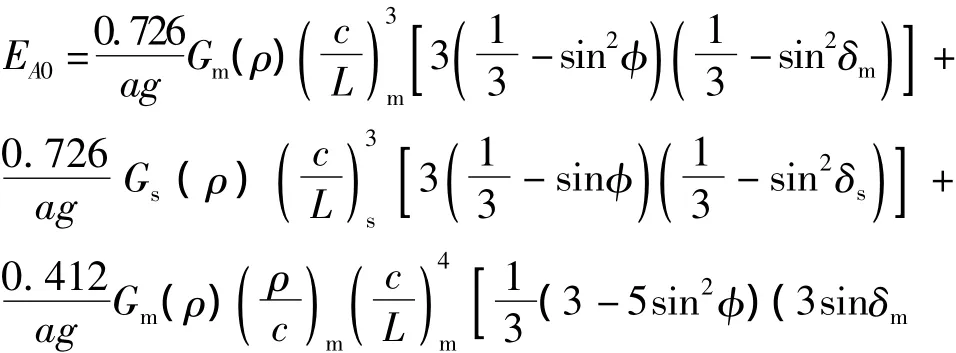

2.2.2.2 体应变固体潮理论值计算公式
由正南北、正东西、垂直方向的线伸缩观测值计算面应变的公式为[7]

将式(16)代入式(12)~(15)可推导出体计算应变固体潮各波类理论值的实用公式。
3 计算固体潮理论值步骤
1)输入计算点(台站)的经度、纬度、计算时刻的年、月、日、时;
2)将地理纬度化为地心纬度并计算出它的正弦和余弦值;

4)求出计算时刻的儒略世纪数T[8];
5)由儒略世纪数T计算天文常数 τ、s、h、p、N、Ps[3,4,6];
6)计算各轨道参数表达式(c/L)m、(c/L)s、λm、λs、βm、βs[3,4,6];
7)求待算点待算时刻的地方恒星时I[2];
8)由黄道坐标转为赤道坐标[3,4,6]。
4 结果验证
笔者将文中推导出的以及倾斜固体潮各波类理论值计算公式在C#中编程实现,并得出计算结果。
为验证计算的正确性,以湖北宜昌地震台为例,计算该台站不同时间段重力固体潮、倾斜固体潮、应变固体潮各波类理论值(重力和倾斜固体潮理论值是基于刚体地球模型),并将相加后的值与地震前兆信息系统EIS2000软件中计算的固体潮理论值进行比较。同样,以该台站重力固体潮为例,将由本文计算的结果与该台站重力观测结果对比。
图1为宜昌台2013-01-01—05日EW分量倾斜固体潮理论值计算结果,从图1可发现两者是十分吻合的。对两组数据进行相关分析得到的相关系数为0.996;对两组数据进行回归分析,得到拟合的线性回归直线的斜率为0.994。

图1 宜昌台2013-01-01—05日EW分量倾斜固体潮理论值计算结果对比Fig.1 Theoretical calculation result comparisons of eastwest tilt earth tide of the Yichang seismostation from January 1 to 5 in 2013
图2为宜昌台2013-01-01—10日SN分量倾斜固体潮理论值计算结果。对两组数据进行相关分析得到的相关系数为0.997,对两组数据进行回归分析,得到拟合的线性回归直线的斜率为0.993。
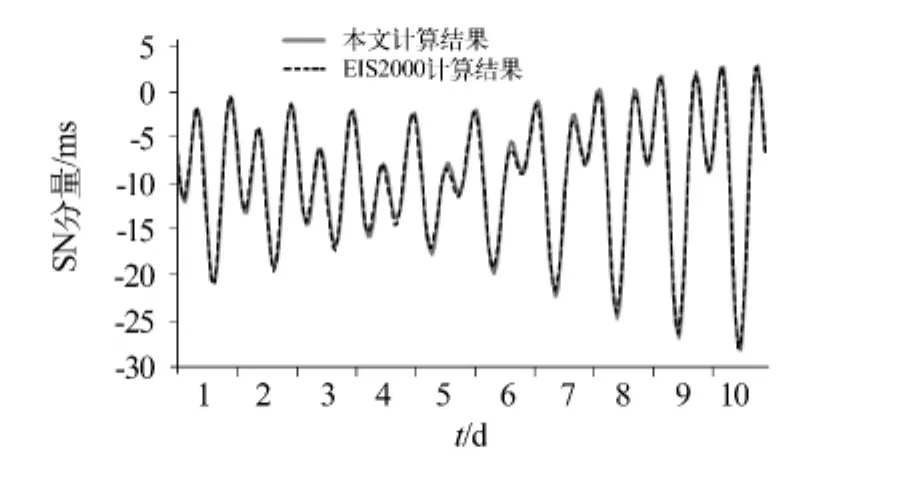
图2 宜昌台2013-01-01—10日SN分量倾斜固体潮理论值计算结果对比Fig.2 Theoretical calculation result comparisons of northsouth tilt earth tide of the Yichang seismostation from January 1 to 10 in 2013
图3为宜昌台2013-01-05—10日重力固体潮理论值计算结果对比图。其相关系数为0.994;其线性回归直线的斜率为0.988。
图4为宜昌台2013-01-10—15日面应变固体潮理论值计算结果对比图。两组数据的相关系数为0.996,线性回归直线斜率为 0.990。

图3 宜昌台2013-01-05—10日重力固体潮理论值计算结果对比Fig.3 Theoretical calculation result comparisons of gravity tide of the Yichang seismostation from January 5 to 10 in 2013
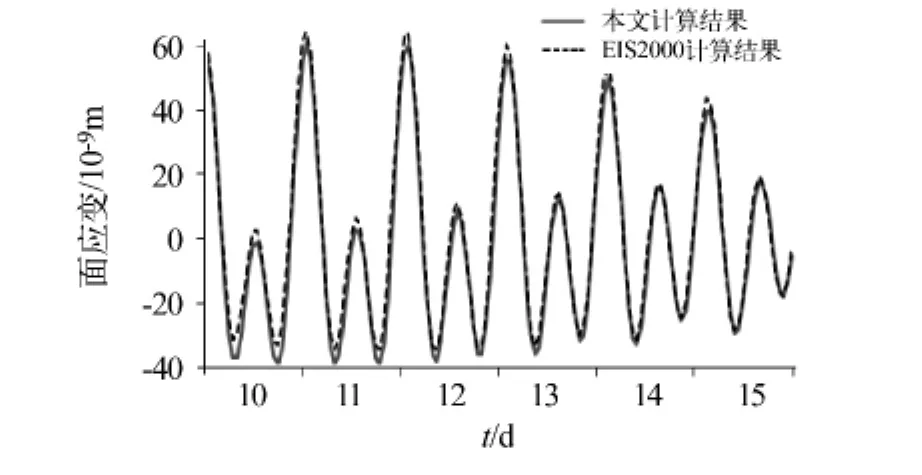
图4 宜昌台2013-01-10—15日面应变固体潮理论值计算结果对比图Fig.4 Theoretical calculation result comparisons of surface tide of the Yichang seismostation from January 10 to 15 in 2013
图5为宜昌台2013-01-05—15日重力固体潮本文计算结果对比图,从图5可见两者趋势较吻合,但存在差异。经分析其原因为:1)本文计算采用的为理想刚体地球模型;2)本文中月亮的起潮位只取至三阶项,太阳的只取至二阶项,公式中所取参数值为近似值;3)固体潮在观测过程中存在零点漂移。

图5 宜昌台2013-01-15—25日重力固体潮计算结果与观测值对比图Fig.5 Calculation result comparisons of gravity tide between calculation and observation of the Yichang seismic station from January 15 to 25 in 2013
对计算结果的分析可以看出,应用本文公式的计算结果与EIS2000软件的计算结果在时间和数值上均较吻合,与观测值也有良好的相关性,证明了本文计算结果的可靠性。
本文中基于拉普拉斯级数展开法推导出的固体潮分波计算公式,易于编程实现,能满足现阶段地震台站的精度要求,但要获得更高精度的潮汐理论值,需采用引潮位展开表计算,并考虑每个波群不同的潮汐因子。
由本文固体潮分波理论值计算方法及计算步骤,在C#中将各种算法编程实现,并封装为带接口的动态链接库,可以实现跨平台、跨操作系统的调用。
1 郗钦文.固体潮汐理论值计算[J].地球物理学报,1982,25(增刊):632- 643.(Xi Qinwen.Theoretical value calculating of solid tidal[J].Chinese Journal of Geophysics,1982,25(Sup.):632 - 643)
2 刘序俨.倾斜固体潮长周期波、全日波、半日波和1/3日波的理论值计算[J].华北地震科学,1987,5(1):138-144.(Liu Xuyan.Tilt solid tide theoretical value calculation of long period wave,wave,semidiurnal wave,1/3 wave[J].North China Earthquake Sciences,1987,5(1):138 -144)
3 许厚泽.固体地球潮汐[M].武汉:湖北科学技术出版社,2010.(Xu Houze.Solid earth tides[M].Wuhan:Hubei Science and Technology Press,2010)
4 吴庆鹏,等.重力与固体潮教程[M].北京:地震出版社,1990.(Wu Qingpeng,et al.Gravity and solid tide tutorial[M].Beijing:Seismological Press,1990)
5 吴庆鹏.重力学与固体潮[M].合肥:中国科学技术大学出版社,1997.(Wu Qingpeng.Gravity and solid tide[M].Hefei:China Science and Technology University Press,1997)
6 唐九安.固体潮资料处理程序[M].兰州地震研究所,1989.(Tang Jiuan.The solid tide data processing program[M].Lanzhou Institute of Seismology,1989)
7 刘澜波.体应变固体潮理论值的计算[J].地震研究,1984,6(7):681 - 687.(Liu Lanbo.Calculation of theoretical values of the volumetric tidal strain[J].Earthquake Research,1984,6(7):681 -687)
8 郜晓亮,荆磊,孙明国.基于MATLAB的重力固体潮理论值计算[J].中国西部科技,2009,8(1):33 -34.(Gao Xiaoliang,Jing Lei and Sun Guoming.Theoretical value calculating of gravity tide based on MATLAB[J].Technology of West China,2009,8(1):33 -34)
THEORETICAL VALUE CALCULATION OF TIDAL PARTIAL WAVE BASED ON LAPLACE SERIES EXPANSION METHOD
Su Rong and Li Shengle
(Key Laboratory of Earthquake Geodesy,Institute of Seismology,CEA,Wuhan430071)
The theoretical formulas and steps of the tilt tide,gravity tide,strain earth tide,which divided into four partial wave:long period wave,wave,semidiurnal wave,1/3 wave were given by the Laplace series expansion method.The above theoretical values can be calculated using C#programming language,and compiled into a dynamic link library.The results can be used as a cross-platform and cross-operating system calls.
earth tide;theoretical value of tidal partial wave;Laplace series expansion method;tide-generating potential;C#
P312.4;P315.0
A
1671-5942(2013)05-00106-04
2013-03-12
国家科技支撑课题(2012BAK19B02-05)
苏融,女,1989年生,硕士研究生,研究方向为固体地球物理,地震前兆数据处理.E-mail:sue.sdau@163.com

