几种插值方法在构建南极冰盖DEM中的比较*
杨元德 熊云琪 王泽民 鄂栋臣
(武汉大学中国南极测绘研究中心,武汉 400079)
几种插值方法在构建南极冰盖DEM中的比较*
杨元德 熊云琪 王泽民 鄂栋臣
(武汉大学中国南极测绘研究中心,武汉 400079)
在南极冰盖选取不同实验区域对常用的六种插值方法进行比较分析,采用均方根预测误差和源数据均方根等评价指标对不同插值方法进行评价,结果表明克里金插值方法更适用于构建南极冰盖DEM。
南极冰盖;DEM;插值方法;均方根;克里金插值方法
1 引言
南极冰盖数字高程模型(DEM,Digital Elevation Model)在南极研究中发挥着重要的作用。它可用于确定分冰岭、冰流盆地、接地线的位置、计算冰流的大小及方向、平衡速度及底部剪应力等;它也是估算冰面温度、降水、下降风的大小和方向的重要参数;精确的地形数据对于利用遥感方法进行南极测图研究也有着十分重要的意义;南极冰盖DEM与冰厚数据相结合,能够计算冰体变形的速率及应变;此外,精确的DEM也是构建南极冰下地形模型的基础[1-6]。表 1给出了基于测高卫星的南极冰盖DEM的发展概况。
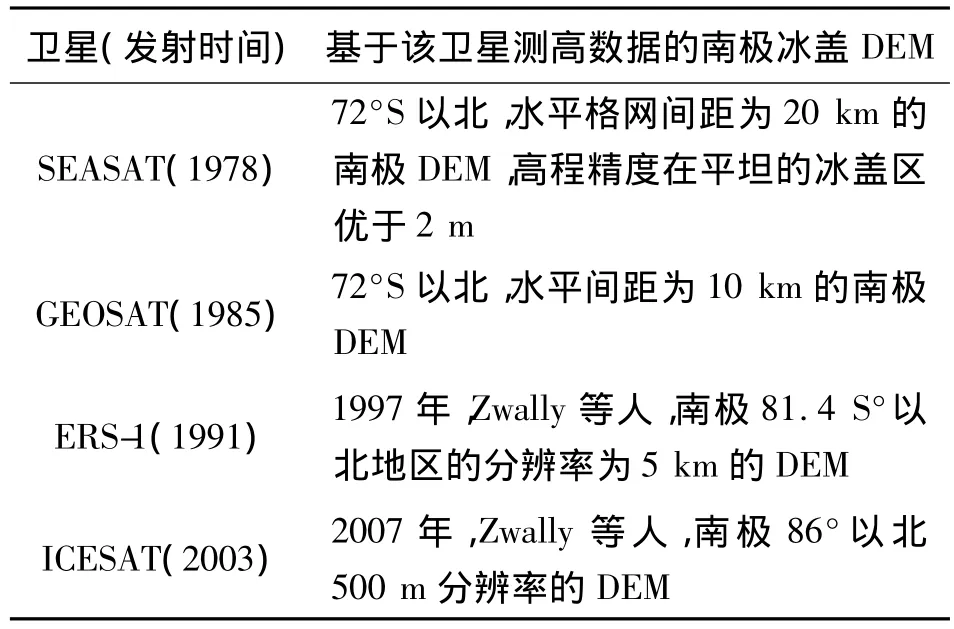
表1 南极冰盖DEM的发展Tab.1 Development of Antarctic ice sheet DEM
测高卫星为南极科学研究提供了丰富的源数据,基于这些卫星测高数据构建南极冰盖DEM时,不同研究者采用了不同的数据插值方法,因此数据插值效果直接影响南极冰盖DEM的精度。本文主要在南极冰盖选取不同地形特征的实验区,通过比较几种常用插值方法的插值效果,选择最适宜构建南极冰盖DEM的插值方法。
2 数据插值方法简介
本文采用的数据插值方法由美国GOLDEN软件公司的Surfer10.1软件提供,且主要对六种插值方法进行比较分析。
反距离加权插值法的插值原理是待插值点邻域内已知离散点属性值的加权平均,权的大小与待插点的邻域内离散点之间的距离有关,是距离k(0≤k≤2,k一般取2)次方的倒数。即:
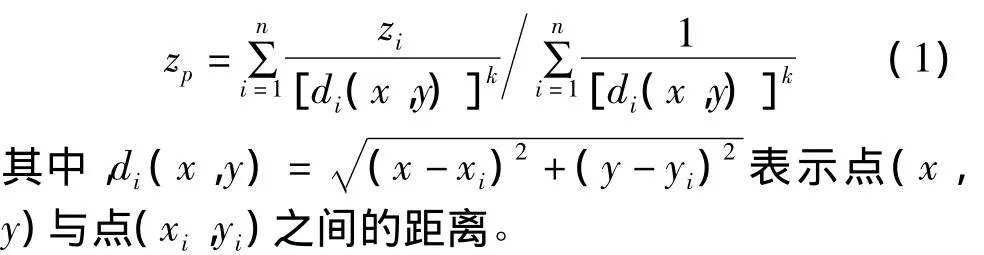
克里金插值方法是在满足无偏估计和最小方差条件的前提下求得估计值。设区域化变量f(x)满足二阶平稳条件,则待插值点P的估计值为

其中fi是n个已知点的函数值,wi是n个已知点的权系数。其中μ为拉格朗日算子,γ(xj-xi)为已知点间的变差函数值,γ(xp-xi)为已知点与待插值点间的变差函数值。
最小曲率法用公式表示为:
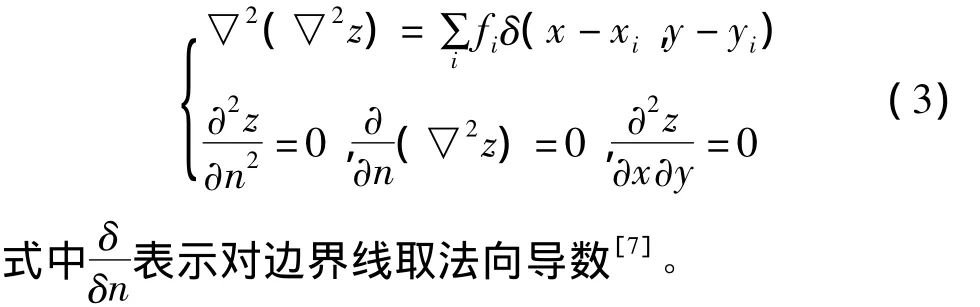
传统的多项式插值方法在Surfer10.1中有三种形式:

最近邻点插值法又称泰森多边形方法,其隐含假设条件是任一网格点P(x,y)的属性值都使用距它最近位置点的属性值,用每一个网格节点的最邻点值作为该点的节点值。假若有一块总面积为s的区域,共有N个网格点n(n=1,2,…,N)。各个网格点的属性值分别为qi(i=1,2,…,N),以各网格点之间连线的垂直平分线,把区域划分为若干个多边形,然后以各个多边形的面积si(i=1,2,…,N)为权系数,计算各网格点的加权平均值,并将其作为区域的平均属性值,即[8]:

假设三角片的3个顶点是A、B、C,其观测值分别为f(A)、f(B)、f(C),任何点相对于该三角形有唯一的重心,其坐标为:

线性插值可写成

由式(6)和式(7),点(x,f(x))可以表示为{(A,f(A));(B,f(B));(C,f(C))}的线性凸组合,也就是说这是一张平面;当0<u、v、w<1时,x位于三角形内部,(x,f(x))形成一个三角片[9]。由以上原理出发,需要求得系数u、v、w,本文采用三角形的3个顶点信息分别获得系数值。
3 插值方法评价指标与实验
3.1 评价指标
插值精度的评定指标概括起来主要分为:1)对于采样点计算的均方根预测误差(RMSPE,Root Mean Square Predictive Error),其值越小说明插值结果越接近真实值,结果越可靠;2)计算源数据得到的残差均方根(RMS),源数据残差均方根用于评价网格数据与源数据的一致性。因此本文主要以这二个指标对插值结果进行评价,并辅之以残差绝对值最大、最小、平均值等参数。
均方根预测误差的计算公式为:
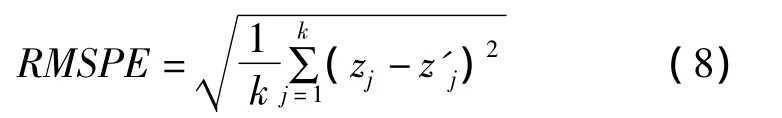
式中k表示用于估计网格数据精度的样点数,zj表示第j(1≤j≤k)个样点插值后高程,z'j表示第j个样点原始高程。
源数据残差均方根计算公式为:

式中n表示整个实验区的用于插值的源数据点数,zi表示第i个插值后高程,z'i表示第i(1≤i≤n)个原始观测高程。
3.2 实验数据和实验区
实验采用的ERS-1数据由欧洲太空局网站(http://www.esa.int/esaCP/index.html)下载。其数据采集时间为ERS-1在Phase E和Phase F工作段采集。ERS-1任务时间段如表2所示。
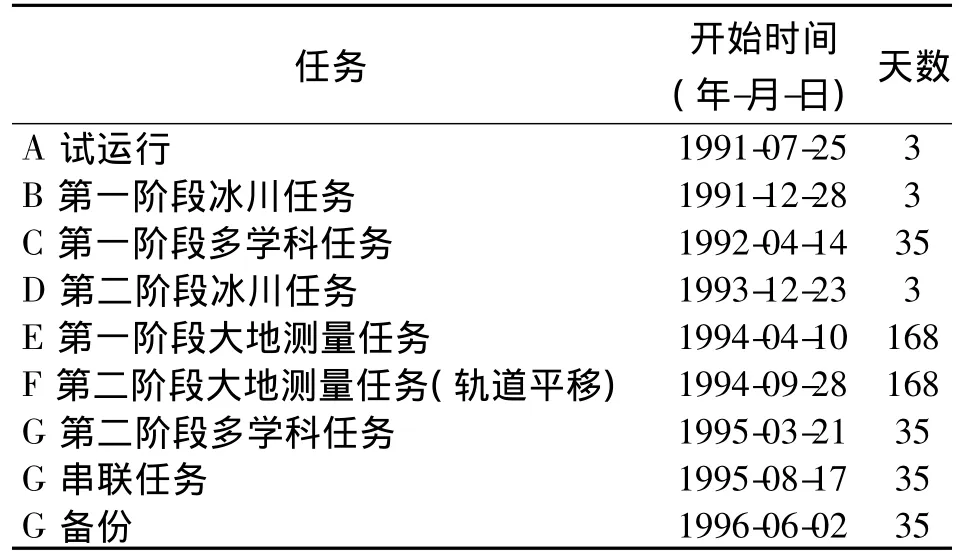
表2 ERS-1任务时间段表Tab.2 ERS-1 mission phase
为选择最佳插值方法,选择的三个地区的地形特征为:横断山脉的地区地形较为复杂,有些区域的高程变化比较急剧,是典型的山区地形;南极半岛地区的地形非常复杂,基岩起伏不平,有大量山峰和山脉,海岸曲折,近海岛屿很多地势陡峭;中山站至DomeA地区的地形比较简单,变化较缓,地势平坦。如表3所示。
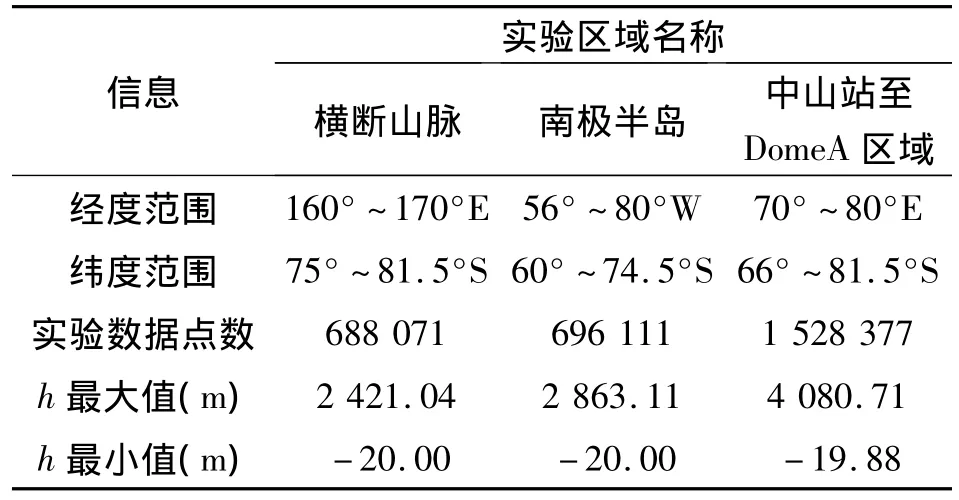
表3 ERS-1数据统计的实验区信息Tab.3 Statistics of ERS-1 data within experimental areas
3.3 实验计算及结论
利用Surfer10.1软件对实验区进行随机均匀采样,在每个实验区均匀随机取约占总点数约5%的采样点。横断山脉、南极半岛、中山站至Dome A三个区域的采样点分别为35 000、35 000和75 000。然后采用有效性评价指标对插值方法进行有效性评价。结果如表4~6。

表4 横断山脉地区不同插值方法评价指标计算结果(单位:m)Tab.4 Comparison of interpolation methods in Trans-Antarctic mountains(unit:m)
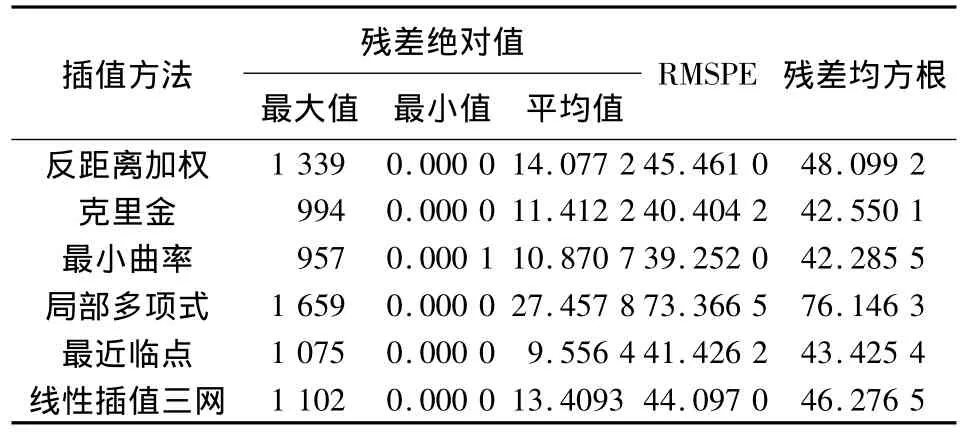
表5 南极半岛地区不同插值方法评价指标计结果(单位:m)Tab.5 Comparison of interpolation methods in Antarctic peninsula(unit:m)
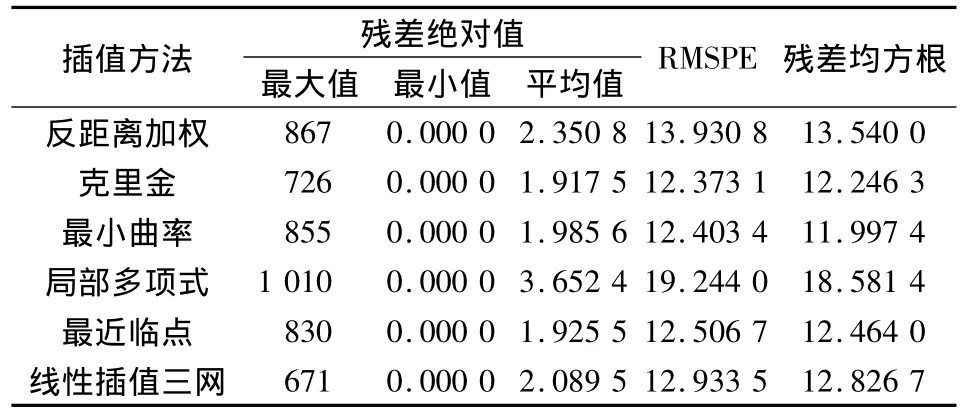
表6 中山站-Dome A地区不同插值方法评价指标计算结果(单位:m)Tab.6 Comparison of interpolation methods in the transit from Zhongshan station to Dome A area(unit:m)
对表4~6分析可以得到:
由RMSPE和残差RMS统计结果可知,最近临点方法在表5、6中较小,但在表4中较大,可见最近临点方法依赖于数据或地形,其插值效果不稳定。而对于线性插值三角网、反距离加权插值、局部多项式插值在三个实验区,无论是残差均值平均值,还是RMSPE和RMS都比较大,这三种插值方法的插值效果较差。而克里金和最小曲率插值算法的RMSPE和RMS最小,说明这两种方法的插值效果最好。为了对克里金插值算法和最小曲率插值效果进一步比较,图1给出了两种方法插值的中山站-Dome A地区等高线图。由图1可以看出,最小曲率的等高线上方出现明显的错误。这是因为最小曲率主要考虑曲面的光滑性,使得插值结果容易失真,绘出的等值线与实际相差较大。综上分析,在南极地区,插值方法效果最好的是克里金插值,其余的几种插值方法都存在不足。
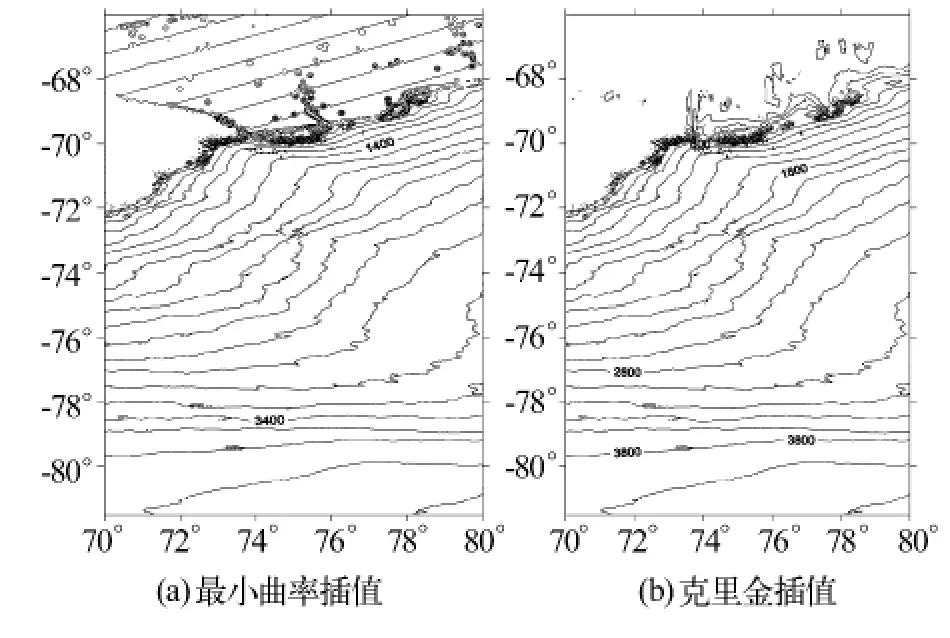
图1 中山站-Dome A地区等高线图Fig.1 Contour map of the transit from Zhongshan station to Dome A area
对比表4~6可以发现表6中残差绝对值均值、RMS和RMSPE明显小于其他两个表格,该结果表明了地形平坦、坡度变化较缓的中山站-Dome A地区插值精度高于地形复杂、地势陡峭的横断山脉和南极半岛,即地形因素对于插值结果的精度具有很大影响,平坦地区插值精度较高,而坡度较大、地形剧烈变化地区插值精度较低。
4 结束语
对比分析结果表明,在众多插值方法中,克里金插值方法有很好的适应性,对于不同复杂程度的地形均能实现有效的空间插值,精度较高,因此建议采用克里金算法构建南极冰盖DEM。从在实验地区的插值效果来看,大部分方法均适用于地势相对平坦的区域,如中山站至DOME A区域,但对于坡度较大、地形剧烈变化地区,有些插值方法出现了较大误差精度也较低,如南极半岛。因此在选择内插方法时,尤其是复杂区域,需要慎重。本文没有对各方法的插值效率、数据分布均匀与否条件下的插值表现进行比较,这也是今后的重点研究方向。
1 张胜凯,等.南极数字高程模型研究进展[J].极地研究,2006,18(4):301 -309(Zhang S k,et al.Progress in Antarctic DEM[J].Polar Research,2006,18(4):301 -309)
2 Budd W F,Jenssen D and Smith I N.A three-dimensional time-dependent model of the West Antarctic ice sheet[J].Ann Glaciol.,1984,5:29 -36.
3 Zwally H J,et al.Surface elevation contours of Greenland and Antarctic ice sheet[J].J Geophys Res.,1983,88:1 589 -1 598.
4 Zwally H J,et al.Ice measurements by GEOSAT radar altimetry[R].The Navy GEOSAT Mission,Johns Hopkins APL Tech Dig,1987,8(2):251-254.
5 Zwally H J,et al.Ice sheet topography,slopes and flow directions from ERS altimetry[A].Florence,Italy:The 3rd ERS Symposium,Euro Space Agency[C].1997.
6 吴宗敏.散乱数据拟合的模型、方法和理论[M].北京:科学出版社,2008.(Wu Z M.Model,method and theories for scattered data fitting[M].Beijing:Science Press,2008)
7 Smith W H F and Wessel P.Gridding with continuous curvature splines in tension[J].Geophysics,1990,55,3:293 -305.
8 顾春雷,杨漾,朱志春.几种建立DEM模型插值方法精度的交叉验证[J].测绘与空间地理信息,2010,34(5):99 -102.(Gu C L,Yang Y and Zhu Z C.Accuracy crossvalidation of several interpolation methods for DEM model[J].Surveying& Spatial Information,2010,34(5):99-102)
9 武俊红,汪云甲.基于Surfer的煤矿等值线空间插值方法有效性评价[J].中国矿业,2007,16(1):108-120.(Wu J H and Wang Y J.Effectiveness evaluation of interpolation methods in coal contour based on Surfer[J].China Mining,2007,16(1):108-120)
COMPARISON OF INTERPOLATION METHODS IN CONSTRUCTING ANTARCTIC ICE SHEET DEM
Yang Yuande,Xiong Yunqi,Wang Zeming and E Dongchen
(Chinese Antarctic Center of Surveying and Mapping,Wuhan University,Wuhan430079)
The paper compared and discussed six commonly used interpolation methods.The interpolation methods were evaluated using the parameters such as the root mean square prediction error and the source data root mean square,within different experimental areas in the Antarctica.The result showed that the Kriging interpolation method is more suitable for constructing the Antarctic ice sheet DEM.
Antarctic ice sheet;Digital Elevation Model(DEM);interpolation method;Root Mean Square(RMS);Kriging interpolation method
P207
A
1671-5942(2013)05-0063-04
2013-02-14
国家自然科学基金(41106163);国家海洋局极地科学重点实验室开发研究基金(KP201102);南北极环境综合考察与评估专项(CHINARE2013-03-03,CHINARE2013-01-03);中央高校基本科研业务费(121047);国家863计划项目(2012AA12A304);国家测绘地理信息局科技项目(极地测绘技术试验)
杨元德,男,副教授,主要从事卫星测高与卫星重力应用研究.E-mail:yuandeyang@whu.edu.cn

