小半径 大底坡溢洪道弯道水流三维流场数值计算分析

董延超 ，曲 洋 ，刘 杰

(1.中水东北勘测设计研究有限责任公司，吉林 长春 130021；2.水利部松辽水利委员会，吉林 长春 130021)

0 引言

20世纪以来，高水头水利枢纽不断兴建，尤其是在高山峡谷中建坝，泄水建筑物在平面布置上难免要出现收缩、扩散和弯道，随之出现的明渠高速水流对水工建筑的影响问题比较突出。近年来随着紊流理论及计算技术的发展，数值模拟的方法逐渐成为工程设计和研究的重要手段，对弯道水流及溢洪道的紊流模拟也日渐增多，研究主要集中应用于模拟天然弯曲河道及溢洪道。1996年王少平、曾扬兵等将Yakhot与Orszagd的RNGk-ε紊流模式推广应用于180°强曲率弯道内的紊流分离流动的数值模拟,，计算在任意曲线坐标下进行，采用通常的控制容积法求解控制方程[1，5]。2001年周茂林，牛志攀等采用k-ε紊流模型结合自由面追踪的VOF方法对桐子林水电站明渠弯道消力池流场进行了三维数值模拟，并与物理模型试验值进行了比较，结果表明，计算值与试验值吻合良好[2]。2005年周勤、伍超等对“S”型溢洪道进行了模型试验和数值模拟研究，经试验优化后的斜槛布置改善了溢洪道水流流态，减小了横向超高[3]。

本文采用VOF方法、笛卡尔网格与部分面积体积障碍模拟法，结合RNGk-ε紊流模型成功地模拟了小半径、大底坡溢洪道陡槽弯道三维复杂紊流流场，对溢洪道弯道流场特性进行充分研究，为工程设计提供参考。

1 物理模型

物理模型以辽宁省汤河水库溢洪道整体水工模型试验为基础，其陡槽弯道属于小半径(r/B≤10)、大底坡形式，弯道内水流特性具有代表性。模型按重力相似准则设计，模型比尺1∶50，模型采用有机玻璃制作。模型试验数据采集使用DJ800型多功能监测系统，采用电容式波高仪测量水位，毕托管式压差流速传感器测量流速。选用50年一遇、100年一遇、1000年一遇3种洪水频率下不同流量进行模型试验。

溢洪道弯道为简单圆弧弯道，从桩号0+170.00至桩号0+288.00，全长118 m，弯道中心半径为210 m，圆心角32°，横断面为矩形，宽25.5 m，底坡为0.09，上、下游均与直段陡槽相接，出口采用底流消能。

2 数学模型

2.1 控制方程

数学模型采用RNGk-ε双方程湍流模型，由Yakhot和Orszag于1986年应用重整化群的方法导出，它和标准k-ε模型很相似，但是考虑了湍流漩涡、低雷诺数流动粘性，可较好地处理高应变率及流线弯曲程度较大的流动。

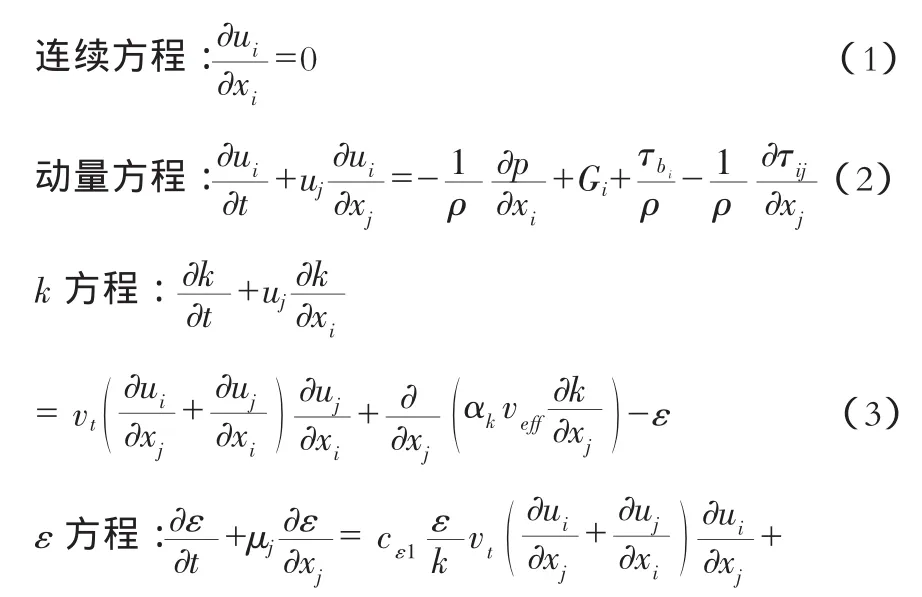
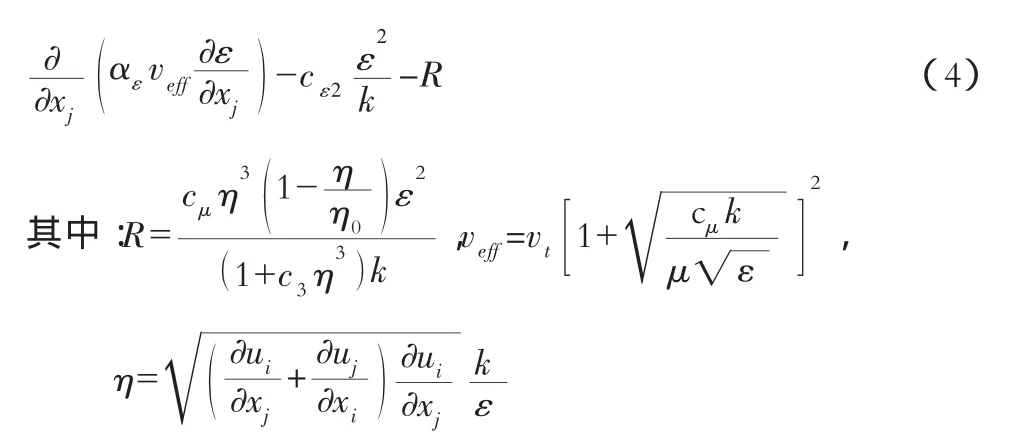
式中：ui是 i方向上的速度分量（i＝1，2，3）；t是时间；xi是在i方向上的坐标；p是压力；ρ是密度；Gi是i方向的单位质量力；τij是粘性应力；τbi是墙体的剪切应力；vt是涡粘性系数；μ 是动力粘性系数。cε1，cε2，cε3，αk，αε，η0和 cμ都是常数。RNG 理论认为 cε1=1.42，cε2=1.63，cε3=0.012，αk=αε=1，η0=4.38 和 cμ=0.085。

2.2 自由水面确定和复杂边界处理

自由水面确定采用高效的VOF法。该方法基本思想是定义体积分数函数：F=F（x，y，z，t）。在单个计算单元中，若F=1，则表示该单元被流体充满；若F=0，则表示它是一个空单元；若0＜F＜1，则表示该单元部分充满流体。

水气界面的跟踪则通过求解连续方程来完成：

其中，t为时间，ui和xi分别为速度分量和坐标分量，自由水面的具体位置则采用几何重建格式来确定，它利用分段近似方法来表示自由水面线。

复杂的几何边界处理引入FAVOR（Fractional Area Volume Obstacle Representation）方法，即部分面积体积障碍模拟法，由 Hirt和 Nichols（1985）[4]提出，是与 VOF 法相似的一种处理复杂几何边界的体积分数方法。FAVOR法是用每个网格内固体的体积分数来确定固体的表面。在FAVOR法中，网格开放部分的宽度等于开放的体积分数与原始网格宽度的乘积，如图1所示。

2.3 计算区域及网格划分

采用笛卡尔结构网格对计算区域进行网格划分。为获得精确数据观察流场特性，对墙壁进行局部网格细化。计算区域由两部分组成：固体障碍物和流体流动区域。正六面体笛卡尔结构网格对整个计算区域划分见图2。

2.4 边界条件与初始条件

入口边界采用流速边界条件。根据不同工况的流量和上游水库水位，计算出进口不同流量条件下的入口流速。上边界采用气体压力边界，其总压力为大气压力。整个溢洪道弯道底板和边墙都按无滑移壁面边界条件处理。紊流壁面采用壁函数来处理，光滑壁面函数为：

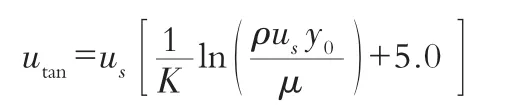
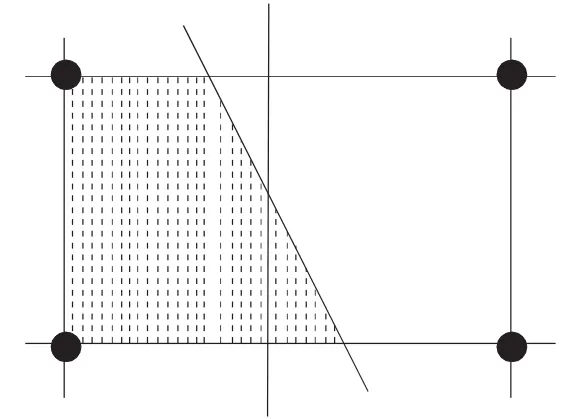
图1 FAVOR网格（阴影为固体）

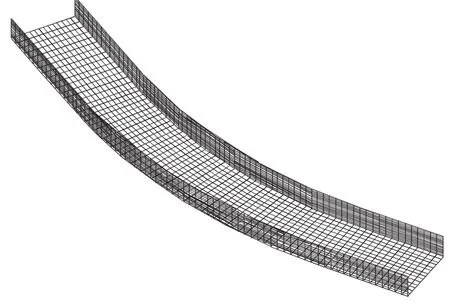
图2 弯道网格划分图

式中：K为卡门常数；μ为动力粘性系数；y0为到壁面的距离；us为墙体剪切速度；utan为流体距离墙体y0处的流速。紊动动能，紊动耗散率。考虑出口紊流发展较完全，出口边界采用自由出流边界条件。假设除压力外，其它所有的流动参数法向梯度均为0。

初始条件的确定参照物理模型试验数据，依据水库水位、泄流量确定入口流速、水深，紊流参数如k和ε的初始值由经验公式计算给出。

2.5 数值计算方法

采用有限体积法对微分方程进行离散，笛卡尔网格划分的控制体为正六面体，交错网格技术把压力p、紊动能k、紊动动能耗散率ε、流体体积VF布置于每一单元体中心，速度矢量和流体面积布置于控制体表面，对控制体进行积分，各变量在相应的网格中离散求解。求解方法采用SIMPLE算法，离散方程式用欠松弛ADI法进行求解。

3 计算结果与分析

3.1 水面形态

由数值模拟结果可知，数值模拟与模型试验的水面形态基本一致，弯道水流水面呈扭曲状，从弯道进口至弯道出口，凹岸水面升高到一最大值后逐渐较小，凸岸水面则一直减少，水面在弯顶下游倾斜最大，弯道水面成下凹扭曲面，弯道下游直槽段水流的折冲现象明显，但急流冲击波的波峰波谷并不明显。图3为100年一遇洪水流量弯道水面形态。

3.2 水面高程

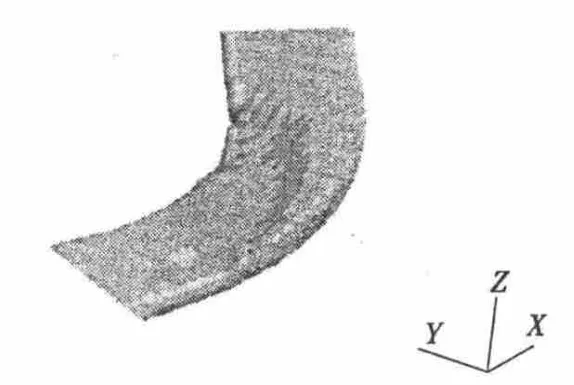
图3 100年一遇洪水流量水面形态图

不同计算工况凹、凸岸水面线数值计算值同试验测量值均吻合较好。弯道水面线凹岸上凸，凸岸下凹。凹岸自进口开始增加，在中部达到最大值，然后逐步减少直到出口；凸岸水面线从弯道进口到弯道出口一直减小。数值模拟与物理试验的弯道段凹岸桩号0+195.50 m与0+258 m两波峰处，最大误差率达到20%，其它处误差率在2%～13%。数值计算结果体现弯道水面变化，但对于冲击波的局部水面雍高表现不明显。图4为100年、1000年一遇流量水面线高程。

图4 洪水流量水面线高程

3.3 断面流速

由数值计算断面流速云图可见，弯道进口处水流流速分布均匀，进入弯道后，在离心力的作用下，各断面流速最大的位置不断向凹岸侧偏移，底层流速小于表层流速，凹岸流速明显大于凸岸，至弯道出口凸岸主流已完全偏向于凹岸。流速的变化趋势表明：小半径、大底坡的体型使得水流急剧偏转，弯道出口水流主流偏转出射，弯道流速分布与弯道水面的倾斜相关。弯道水流出口断面凹岸处数值计算和试验流速数值误差偏大，其它部位基本吻合。弯道流速的误差与试验测量误差和弯道水流不同时刻波动较大有关。总体来说三维数值计算结果可体现弯道水流流速的特性。图5为100年一遇洪水流量断面流速云图，表1为100年一遇洪水断面流速对比表。

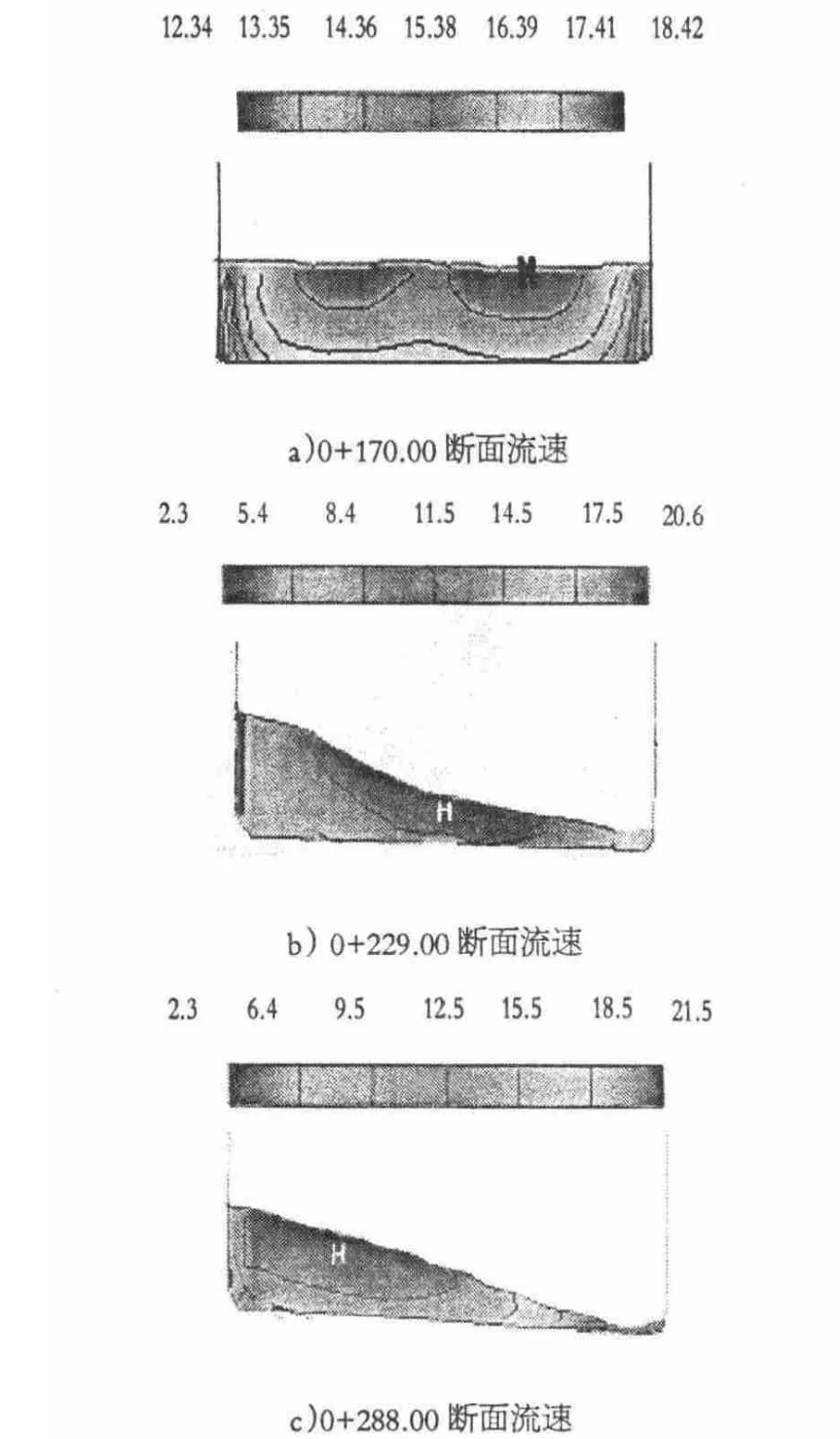
图5 100年一遇洪水流量断面流速云图

表1 100年一遇洪水断面流速对比表

3.4 流场分析

由图6弯道流速矢量图可见，在弯道弯顶上游水流保持原有流向，与弯道轴线成较大角度，弯道下游水流随边墙偏转，与弯道轴线夹角减小，弯道出口折向弯道下游直槽凸岸侧，弯道水流折冲随流量变大逐渐减弱。

4 结语

1）针对溢洪道陡槽弯道工程实例，采用RNGk-ε紊流模型与流体体积分数(VOF)法相结合，FAVOR方法构造复杂边界，成功地模拟了溢洪道陡槽弯道三维紊流流场,计算值与试验值误差率较小，同时获得物理实验没有测量的溢洪道沿程水流结构和流速场分布规律，数值模拟与物理模型试验相互辅助将能更好地研究弯道水流的水力特性。

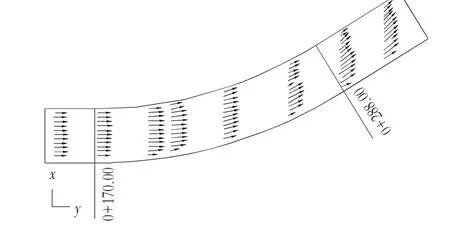
图6 100年一遇洪水弯道流速矢量图

2）溢洪道急流弯道的水流三维紊流数值模拟，详细揭示流场的时均流特性和紊动特性，解决了实际工程问题，丰富了溢洪道弯道水流的理论，为溢洪道弯道水流运动规律水力特性的研究提供了新的方法。

3）RNGk-ε紊流数学模型结合VOF法对于一般的三维流场计算具有普遍意义，便于进行多工况、多方案比较，较模型实验花费少、适应能力强，能提供更详细水力特性资料，是复杂水工建筑物体型优化的有效手段。

[1]王少平，曾扬兵，等.用RNG k-ε模式数值模拟180°弯道内的紊流分离流动[J].力学学报，1996（3）：257-263.

[2]周茂林，牛志攀，等.桐子林水电站明渠弯道流场三维数值模拟[J].人民长江，2011（10）：142-144.

[3]周勤，伍超，等.“S”型溢洪道水流特性试验与数值模拟研究[J].水力发电学报，2005（3）：78-82.

[4]Hirt,C.W.,and Sicilian,J.M..A porosity technique for the definition of obstacles in rectangular cell meshes[J].Proc.,4th Int.Conf.Ship Hydro.,National Academy of Science,Washington,D.C.,1985：1-19.

[5]高伟，杨中华.弯道水流特性和数值模拟方法研究进展[J].水电能源科学，2009（1）：113-116.