基于组合混沌的伪随机数算法研究
张丽娜,何 远,窦琼英,罗桂兰,朱 敏,陈瑞婿
(大理学院数学与计算机学院,云南大理 671003)
在无线通信系统中,通信安全是设计者必须考虑的问题。目前,针对不同的通信系统已经提出了相关的安全协议,但是这些协议往往设计复杂,对硬件要求较高,同时增加了成本。对于计算和存储资源都有限的嵌入式系统,如RFID系统、无线传感器网络等,在实际使用时越来越多的倾向采用伪随机数来进行系统安全通信的设计〔1〕,所以对伪随机数算法的研究具有重要的意义。
伪随机数发生器广泛应用于信息安全、数字通信等诸多重要领域。产生伪随机数的方法很多,如线性同余法反馈位移寄存器法等等。混沌算法的出现为产生随机数提供了一种新的思路。文献〔2-4〕利用混沌系统生成随机密钥流,该密钥流直接用于掩盖明文,实现混沌序列加解密,但这类加密方案存在混沌随机序列离散化后导致的短周期问题。所以本文采用组合混沌映射算法进行改进。
1 组合混沌映射伪随机数发生器
混沌现象是指在确定系统中出现的一种无规则、类似随机的现象,产生的序列具有非周期、不可预测、对初始条件和参数极端敏感性等特点。混沌产生的序列具有随机性,但混沌系统又可以用确定的计算公式表示,利用几个控制参数就可以恢复混沌序列,传递这些参数就可以实现数据的加解密。
1.1 Logistic混沌映射 Logistic混沌映射是一类非常简单的一维非线性迭代方程,应用广泛的动力学系统,其迭代公式为:
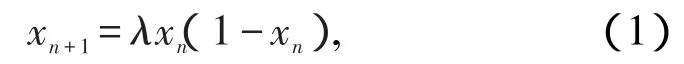
式中0<λ≤4,λ为分形参数。当3.5699…<λ≤4时,系统处于混沌状态。取任意初值X,可迭代出一个确定的序列X1,X2,X3…,Xn,对于不同的λ值,系统将呈现不同的状态,随着参数λ的增加,系统不断经历倍周期分叉,最终达到混沌状态〔5〕。但Logistic混沌映射存在均匀性不够好等方面的缺陷〔6〕。
1.2 Tent混沌映射 Tent映射又称为帐篷映射,其迭代公式为:
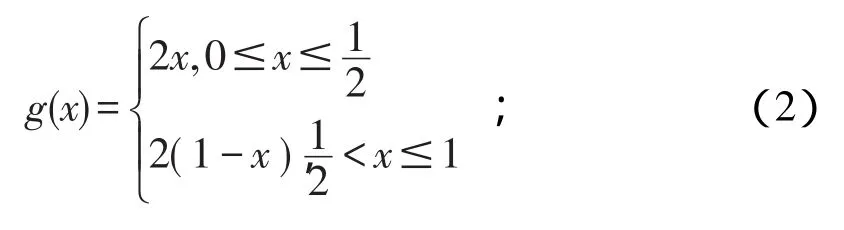
Tent映射经过伯努利移位〔7〕,可变换为:
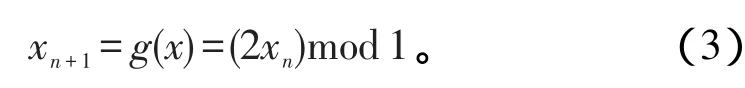
在Tent映射过程中,先给定一个初始值来产生足够长的迭代值,理论上混沌可以产生随机数,但在Tent映射迭代过程中,由于计算机字长有限,小数部分的二进制序列经过一定次数的无符号左移运算将趋向于零,即趋向Tent映射的不动点。仔细分析迭代序列不难发现,序列中存在小周期现象。
1.3 组合混沌映射 文献〔8〕证明了在两个独立的离散非负周期序列 f1(n),f2(n)为常数序列,N1为序列 f1(n)的最小整数周期,N2为序列 f2(n)的最小整数周期,且N1≠N2,则两个序列复合运算产生的新序列 f1(n)Θf2(n)最小整数周期为N1和N2的最小公倍数。其中序列复合运算符号Θ取相加“+”、相减“-”、相乘“·”之一。这为延长混沌最小周期提供了理论基础。
为了提高Logistic混沌映射的精度,也为了降低Tent混沌映射在选取初值时的要求,延长混沌的最小周期,本文将两者进行结合,使其在选取任意初值时都能得到良好的伪随机序列。先由Logistic混沌映射和Tent混沌映射,生成二维数据,通过降维组合成一维混沌。组合的混沌迭代公式为:
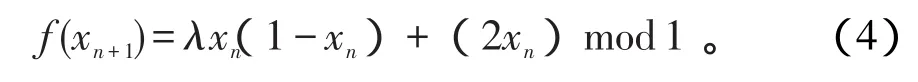
取初值x0,λ取3.5699~4之间的任意值,代入组合函数中进行n次迭代得到随机序列{xn}。具体流程如下:
第一步:取初值x0(x0应避免落入到小周期点内),记入标识组z,z(1)=x0,i=j=1;
第二步:以xn式进行迭代,i自增1,产生x序列;
第三步:如果迭代到最大次数,则跳转到第五步;否则:若x(i)={0,0.25,0.5,0.75}或x(i)=x(i-k),k-{0,1,2,3,4}(即落入不动点或5周期以内的小循环),进入第四步,否则返回第二步;
第四步:改变迭代初值x(i)=z(j+1)=z(j)+a,j=j+1,返回第二步。
第五步:结束。
2 实验验证
对改进后算法的初值敏感性、随机性、遍历性等混沌特性进行测试,结果表明算法仍具有混沌特性。初值x0取0.861进行500次迭代,得到一个既不收敛,也不呈周期运动的“杂乱无章”的随机序列,如图1所示,表明算法可产生较好的伪随机序列。
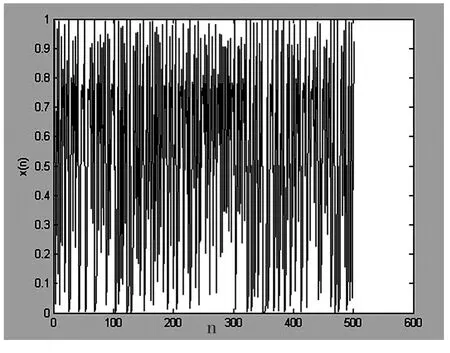
图1 改进的混沌随机数产生算法的混沌序列时序图
但某种算法产生的伪随机数是否是真正意义上的随机数,需要对所产生的随机数进行进一步检验,一般通过序列是否满足随机数所要求的参数检验,均匀性检验,独立性检验等特征来判断〔9〕,如果通过则说明算法能产生良好的随机数序列。
2.1 参数检验 均匀随机数的参数检验时检验出某个发生器产生的随机数序列{xi}的均值、方差、一阶矩阵、二阶矩阵与均匀分布的理论值是否有明显差异〔10-11〕。
2.2 均匀性检验 随机数的均匀性是用来检验由某个发生器产生的随机数序列{xi}是否均匀地分布在(0,1)区间上,也就是检验经验频率与理论频率的差异是否显著。
假设{xi}均匀分布在(0,1)上,用x2检验的方法来看此假设下的计量及其分布。我们将(0,1)等分为k个子区间 I1,I2,…,Ik,则把{xi}等分为k组,记{xi}中落入区间样本个数为nj(j=1,2,…,k),则落
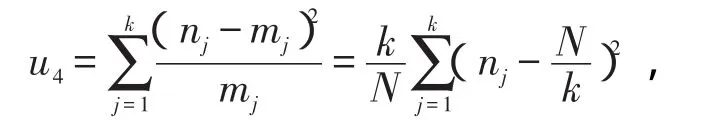
此式渐进服从x2(k-1)。查对应x2分布表的分布临界值为123.23,若u4<123.23则通过均匀性检验。
2.3 独立性检验 独立性检验是检查随机序列之间的统计相关性是否显著,若两个随机变量独立,则他们的相关系数为零。样本的k阶自相关系数若||u5<1.96,则通过独立性检验。
2.43 种方法统计检验结果比较 取初值x0为0.861,分别用样本容量为100,1000,10000进行统计检验,结果见表1。从表1可看出,Logistic混沌映射的均匀性较差,Tent混沌映射未通过参数性检验,组合的混沌映射在样本为100时通过所有检验,明显改善了Logistic混沌映射与Tent混沌映射的缺陷。样本大于1000时组合混沌的独立性还是存在一定的问题,需进一步进行改善。
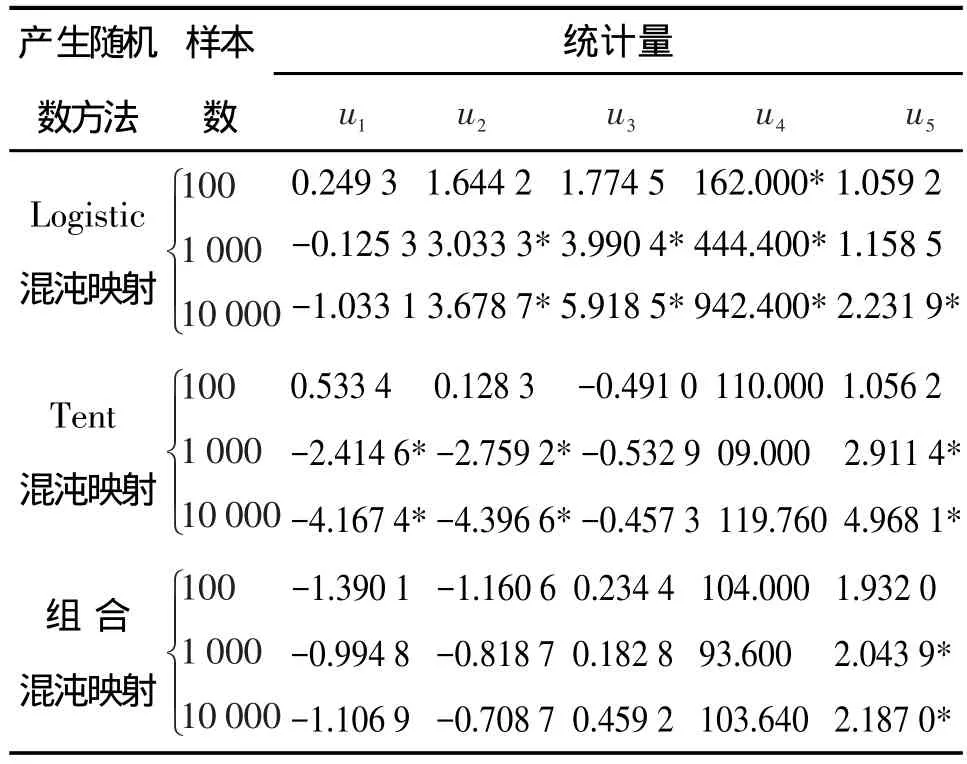
表1 3种方法统计检验结果比较
3 结束语
改进的混沌算法是由Logistic混沌映射与Tent混沌映射组合而成,性能得到很大的改善。组合过程中虽然变成了二维映射,但计算仍是简单的,算法只需要提供一个映射公式,初值和参数就可得到伪随机序列,不必存储多个序列的值,大大节省了存储空间。算法具有一定的实用性。
〔1〕秦雪丽,程明,李伟.基于钟控非线性序列的RFID伪随机数发生器设计〔J〕.计算机应用,2009(11):112-115.
〔2〕Wang Qianxue,Christophe Guyeux,Jacques M Bahi.A novel pseudo-random number generator based on discrete chaotic iterations〔C〕//The First International Conference on Evolving Internet.2009:71-76.
〔3〕Chen Zhuo,Zhang Zhengwen,Jiang Nan.A Session Key Generator Based on Chaotic Sequence〔C〕//International Conference on Computer Science and Software Engineering.2008:635-637.
〔4〕孙晓辉,林秋华,郝育闻.基于组合混沌映射的伪随机数发生器〔J〕.仪器仪表学报,2006,27(6):805-807.
〔5〕韩双霜,闵乐泉,臧鸿雁.基于离散广义混沌同步定理的伪随机数生成器设计及性能分析〔J〕.计算机应用研究,2013,30(5):1511-1514.
〔6〕郑晓丽,姜迪刚.混沌分组密码抗差分密码攻击的分析〔J〕.通信技术,2013(1):40-42.
〔7〕肖旭韬,张雪锋.基于线性反馈移位寄存器和组合猫映射的伪随机序列生成方法〔J〕.计算机应用研究,2013,30(1):161-164.
〔8〕孙克辉,贺少波,何毅,等.混沌伪随机序列的谱熵复杂性分析〔J〕.物理学报,2013,62(1):10501-10501.
〔9〕郭利.基于混沌理论的无穷维伪随机数发生方法及其统计特征〔D〕.武汉:武汉理工大学,2009:11.
〔10〕王光义,袁方.级联混沌及其动力学特性研究〔J〕.物理学报,2013(2):103-112.
〔11〕王涛,王焕.改进的自适应混沌差分进化算法〔J〕.计算机系统应用,2013(2):138-141.

