透视误差对动作技术分析结果的影响及其修正
王晓刚
在用单台摄像机对运动人体进行平面摄影摄像测量时,通常假设运动人体是在垂直于摄像机主光轴的运动平面内运动的,但实际情况并非如此。一般情况下,由于拍摄距离较远,人体移出运动平面时所产生的透视误差可以忽略。因此,大多数研究者在研究时并不会考虑此误差对测量结果的影响。
上世纪八十年代,我国学者卢青(1984)[1]曾对因摄像机主光轴与运动平面不垂直所造成的透视误差情况进行过讨论。而国外学者 Li等人(1990)[2]也曾利用已知环节长度和位置的方法来研究透视误差对测量结果的影响。Miller等人(1980)[3]则提出用一台摄像机拍摄刚体上三个已知空间位置的标志点的方法,来确定其三维坐标。郭珩等人(2008)[4]也曾分析讨论了光学三维测量中透视成像造成的误差并提出了修正算法。但使用这些方法的前提条件是环节长度已知,且至少有一个标志点的空间位置是已知的。因此,当拍摄物不是刚体时(例如人体组织),上述方法则会失效。
本文将介绍两种估测和修正透视误差的方法,目的是为了说明在影像测量过程中透视误差不容忽视,我们可以通过简易可行的方法对其进行修正。
1 透视误差产生的原理及理论修正方法
对透视误差大小的估测,最简便的方法就是利用相似三角形的原理(见图1)。
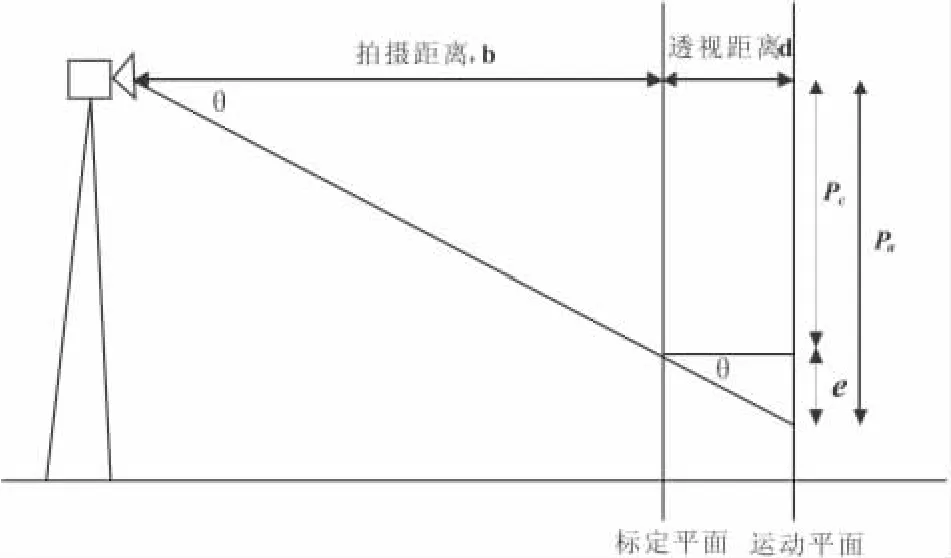
图1 透视误差产生的原理图
由图1可以看出,设拍摄距离为b,透视距离为d,Pc为解析得到的物体垂直距离,Pa为实际的物体垂直距离,Pa与Pc的关系为:
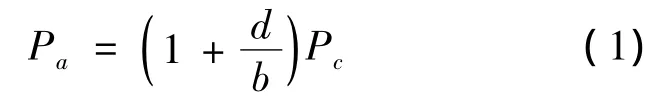
则误差e的值为:

设 b=15m,d=0.15m,Pc=0.7m,则根据等式(1)和(2)可以求出:
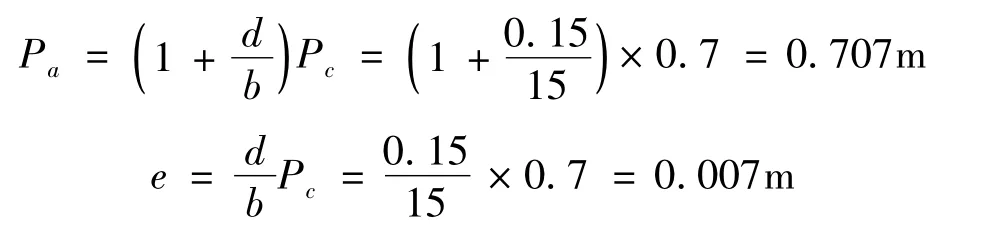
若物体水平方向距离亦为0.7m,则总误差et由此可以看出,在d和Pc不变的情况下,b的值越大(也就是拍摄距离越长),误差越小。但这只是理论分析的结果,在实际拍摄中,由于拍摄距离的增加,可能会影响人体成像的清晰度,因此拍摄距离的适宜长度应该在某一范围之内。
公式(1)和(2)说明,估测和修正透视误差的前提条件是,拍摄距离和透视距离必须已知。通常情况下拍摄距离可以直接测得,而透视距离也可以通过多种方法进行估测。本文将介绍两种估测透视距离的方法。第一种方法,是利用测力台数据,对人体行走过程中透视距离进行估测,用来计算关节作用力和肌肉力矩;第二种方法,是在对铅球运动员的动作技术进行分析时,通过铅球着地点的位置来估测透视距离。
2 修正实例
2.1 平面步态分析实例
在平面逆动力学步态研究中,受试者的行走路线通常不会是一条严格的直线,会因左右摇摆而产生透视误差。为研究此误差对测量结果的影响,我们对一名正常人行走过程进行了拍摄。拍摄使用CASIO FH25数码摄像机,拍摄频率为120Hz;拍摄距离b=4.7m,身体重心至足底压力中心的距离(透视距离)d=0.151m,脚的标志点至视场边缘的距离,即 pc=0.7m。
通过等式(1)和(2)可以算出,pa=0.722m,e=0.022m。若脚的标志点与摄像机主光轴的水平距离同样是0.7m,那么经修正后,踝关节作用力的垂直分量和水平分量变化不明显。其原因是上述两个力的分量的计算取决于地面反作用力和重力,并不受透视误差的影响。而肌肉力矩的计算结果受透视误差影响较为明显(见图2)。例如,踝关节跖屈峰值力矩修正后比修正前增加了27%。在对膝关节和髋关节的逆动力学计算过程中,也同样出现了上述趋势。
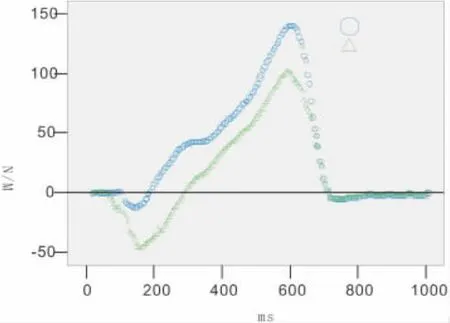
图2 修正前后踝关节力矩比较
2.2 掷铅球投掷距离实验验证
在对铅球运动员的出手速度进行分析时,如果铅球出手点或铅球飞行轨迹所在平面与标定平面不一致,就会产生透视误差,从而使根据视频解析得到的出手速度等参数产生偏差。如图3所示,若d为铅球飞行过程中某点的透视距离(铅球与标定平面的垂直距离),xL与yL为铅球落地点相对标定平面的位置坐标。则根据相似三角形的理论,可以得到下述等式:
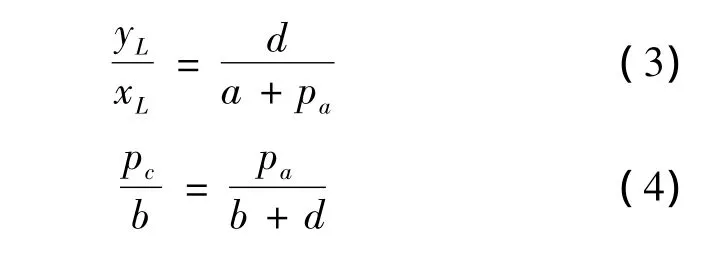
则透视距离
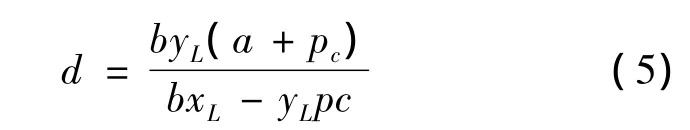
可将通过等式(5)计算得到的透视距离代入等式(1)和(2)中,以计算修正后的铅球出手位置。
另一种推算透视距离d的方法,是假设投出的铅球在空中的飞行轨迹不受空气阻力的影响,呈抛物线轨迹飞行。因此,通过公式我们便可根据解析后计算得到的重力加速度与实际重力加速度进行比较,利用最优化算法,来准确估算铅球实际的出手位置。
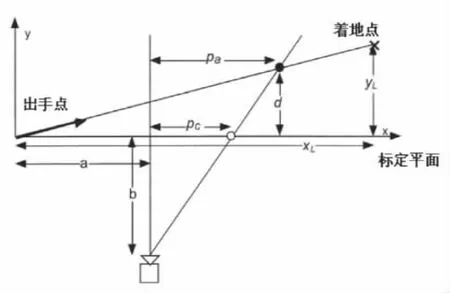
图3 铅球投掷过程中的透视误差示意图
利用等式(3)、(4)、(5)可以很方便地估测出铅球出手时刻的位置坐标。当铅球经过摄像机主光轴附近时,修正系数最小;随着铅球远离摄像机主光轴,修正系数逐渐增加。
为了验证上述修正方法在实际拍摄中的有效性,特邀请一名铅球运动员(国家二级运动员,身高:1.83m;体重:89kg;试投次数:14次)进行投掷实验。拍摄采用一台CASIO FH25数码摄像机,拍摄频率为120Hz。摄像机架设于运动员身体右侧,主光轴垂直于运动平面X轴(见图4),拍摄距离为15m,机高1.2m。在运动员试投前对摄像机进行标定,标定平面为XY平面。
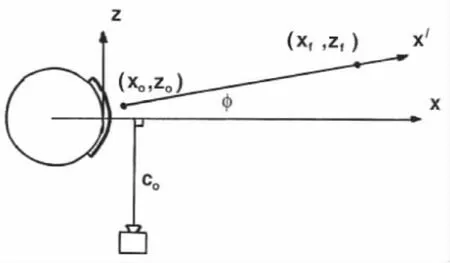
图4 掷铅球实验拍摄现场示意图
以第四次试投为例,在对解析得到的铅球出手位置进行修正后,铅球的出手速度由解析时的10.58m/s增加到10.92m/s(3.2%)。修正值与实测值的误差范围在1cm以内。14次试投中修正值与解析值的比较结果见图5。平均修正值为0.54m。
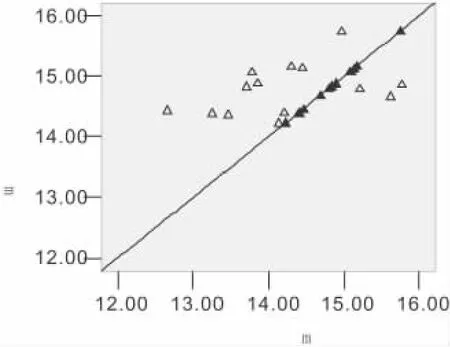
图5 铅球投掷距离的解析值与修正值比较
3 讨论
在多数情况下,研究者通常会忽略影像测量中的透视误差对测量结果带来的影响,但是,这很有可能会使测量结果的精度下降或者得到完全错误的结论。有 制 造 商 曾 经 (Motion AnalysisTM,Koff,1990)[5]指出,在进行平面摄影测量时,系统误差应该在1mm以内。如果透视误差为15.1cm(拍摄距离的3%),那么对踝关节标志点位移坐标的误差可以达到透视误差值的30倍。虽然3cm的位移误差很小,但在对关节力矩进行测量时,如果关节力臂误差达到3cm,则会对测量结果产生很大影响;而对于关节作用力来说,由于其不受力的作用位置的影响,因此透视误差对其计算结果的影响不大。
在对掷铅球的出手速度和投掷距离进行估测时,铅球出手位置的透视误差对估测结果也会产生较大的影响。在此情况下,可以利用两个与解析参数无关联的参数(实测得到的铅球落地位置坐标和已知的重力加速度g)对透视误差进行修正。此方法可以有效地减小因透视误差带来的影响。实验证明,对铅球落地位置的预测结果误差在1cm以内。
上述两个例子说明,利用非解析参数对透视距离d进行估测,可以简单方便地减小此类误差对测量结果的影响。在对掷铅球动作进行分析时,如果透视误差可以被很好的修正,我们完全可以用一台摄像机完成拍摄工作,且对铅球飞行距离的预测结果误差在1cm以内。而这一精度很可能高于利用两台摄像机进行三维测量时的测量精度。
[1] 卢青.高速摄影影片数据的误差源及其处理方法(一)[J].江苏体育科技,1984(5):21~24.
[2] Li,JA,Bryant JT,Stevenson JM.Single camera photogrammetric technique for restricted 3D motion analysis[J].Journal of Biomedical Engineering,1990(12):69 ~74.
[3] Miller NR,Shapiro R,McLaughlin TM.A technique for obtaining spatial kinematic parameters of segments of biomechanical systems from cinematographic data[J].Journal of biomechanics,1980(13):535~547.
[4] 郭珩,赵海波,姜春宝.三维测量中透视成像造成的误差及修正[J].大视野,2008(7):35~36.
[5] Koff DG.Accuracy and precision of the ExpertVision 3-D Motion Analysis Systems[J].Motion Analysis Corporation,Santa Rosa,CA.1990.

