气泡射流载荷作用下圆柱壳动态响应＊

王诗平，郭 君，张忠宇，陈海龙，孙 丰

（哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨 150001）

无论是实战还是实船实验均表明，水下爆炸气泡运动所产生的载荷可以对水中结构物造成致命的打击［1－4］。尤其是药包在水中结构物正下方爆炸［5］，气泡脉动引起气泡周围水质点运动，也叫滞后流，引起水中结构物中垂、中拱低频振动，对水中结构物的总纵强度产生不利的影响。如果中横剖面强度不足，结构物还可能被折断。而且水下爆炸气泡脉动对水中结构物上安装的频率为数十赫兹的设备造成极大危害［6］。除此之外，从水下爆炸实验中也能看到，气泡坍塌产生的高速射流对水中结构产生冲击，这股高速射流会对水中结构造成严重的局部损伤［7－8］，严重时可能导致水中结构完全丧失生命力［9］。

虽然三维水下爆炸气泡动力学数值模型能模拟气泡坍塌形成射流的现象［10－11］，但是由于气泡与水中结构物等之间的相互作用非常复杂，且药包距离结构较近时计算容易发散、工程应用性不强，气泡射流的许多现象和本质仍然没有被揭示。目前，对气泡近距离爆炸产生的射流冲击毁伤的研究，尚未形成一套成熟的方法。

本文中，主要采用如下方法计算水中结构物射流载荷。首先，给出圆柱壳附近不同药量、不同水深条件下气泡射流能直接作用在圆柱壳表面的范围。在圆柱壳附近气泡脉动的数值模拟基础上，假设圆柱壳附近气泡的位移γ可以分解为自由场中气泡由于浮力产生位移γ1（无圆柱壳对气泡吸引的影响）和圆柱壳对气泡吸引产生位移γ2（无浮力的影响）的和，即：

其次，建立简化射流模型，基于DAA方法［12－13］，对射流冲击下圆柱壳板架所产生的毁伤效应进行研究，分析破坏形式，为水下爆炸气泡射流对船体的毁伤提供参考。

1 气泡射流直接作用范围的确定

取一般情况，假设圆柱壳直径为10m，设药包质量分别为100、200、500和1000kg，水深分别为50、100、150和200m。在自由场中采用三维边界元程序计算气泡在浮力作用下的上浮量γ1。边界附近采用三维气泡程序计算直径为10m圆柱壳附近无浮力作用下气泡朝向圆柱壳的运动位移γ2，本文中通过数值模拟得到γ2＝0.9。计算得到气泡产生直接朝向圆柱壳射流范围如图1～2所示。

从图1～2可以看出，在等药量条件下，药包爆炸深度越深，气泡射流范围越小；等水深条件下，药量越小，气泡射流范围也越小。对比图1和2，在定药量条件下，圆柱壳上部直接射流区域随水深影响不大，下部随水深影响较大，在定水深条件下，水深较大时，圆柱壳上部和下部随药量的影响均较大，水深越深，影响区域越接近圆形。

图1 定药量、不同水深条件下气泡对圆柱壳产生直接射流范围Fig.1 Direct bubble jet zone toward submarine with different water depth in certain charge weight

确定气泡对圆柱壳产生直接射流的范围后，基于DAA方法，采用水柱冲击模型进行计算，具体的计算方法如下。

2 气泡射流载荷的计算

2.1 理论模型

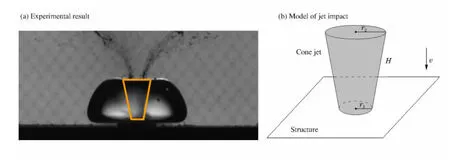
图3 水柱冲击结构模型Fig.3 Model of jet impact on structure

气泡射流对结构冲击的实验结果如图3（a）所示，射流形状近似为圆台形。假定射流为圆台形，上下底面半径大小分别为r1和r2，射流长度为H，射流以速度v冲击板架，如图3（b）所示。假设流体无黏、无旋，可压缩，且不考虑气垫效应。φ为扰动速度势，则流体域的控制方程为：

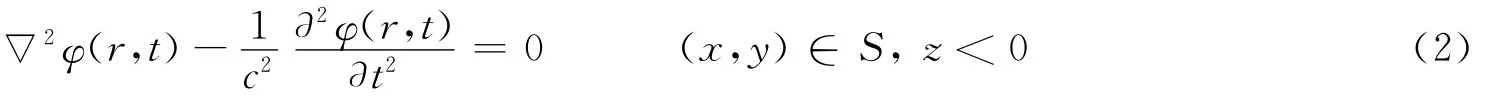
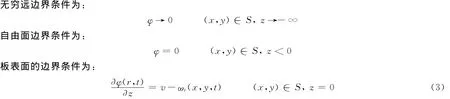
式中：v为水柱的冲击速度，ωt为平板的弹性振动速度。双渐进方程为：

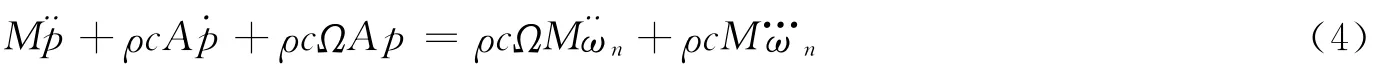
由伯努利方程，约去高阶项，得：

联立式（2）～（5）即可求解。

采用Fortran与Abaqus接口程序，其中结构部分采用Abaqus进行求解，流体部分采用基于流固耦合DAA算法的Fortran子程序求解，实现结构与流体的耦合。

2.2 有效性验证

Y.C.Huang等［13］给出了较低速度水柱冲击下水锤压力的简化计算公式：

式中：p0表示波前压力，ρ0表示波前水密度，p1表示波后压力，c为流体声速，v为射流冲击速度。

用式（6）估算气泡水射流作用在结构上产生的压力幅值。以射流速度v＝100m／s为例，取声速c＝1500m／s，可以计算水柱冲击压力为150MPa。选取直径为0.9m、长为1m的圆柱形水柱，以100m／s的速度冲击尺寸为20m×20m×0.1m的方板，水柱冲击载荷如图4所示。方板压力峰值为149.94MPa，与经验公式吻合，证明了本文数值方法有效性。

2.3 算 例

图4 水柱冲击方板的压力曲线Fig.4 Pressure curve of liquid jet on structure

采用加筋圆柱壳结构，圆柱壳半径为5m，板厚为10mm，加筋圆柱壳纵向布置两条T型加强筋。为了保证计算效率和精度，将冲击区域网格进行加密且过渡处理，材料密度为7 780kg／m3，泊松比为0.281，屈服强度为355MPa，材料的等效塑性应变的失效应变为0.25。加筋圆柱壳的平面图与有限元模型如图5所示。气泡射流速度采用气泡射流端点的速度。水下爆炸气泡射流冲击的速度为约102m／s量级，不失一般性，选用射流冲击速度分别为100和150m／s，通过下面的计算发现，圆柱壳分别出现了塑性变形和破口。

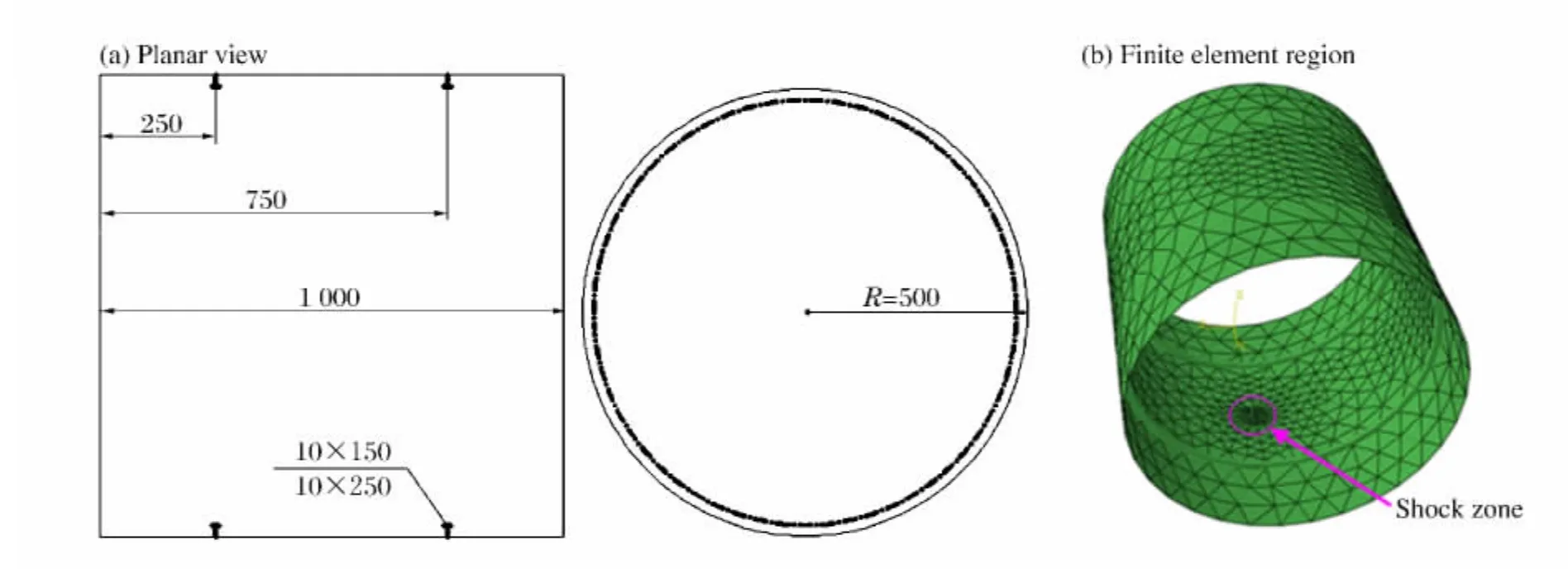
图5 加筋圆柱壳模型Fig.5 Model of stiffened cylindrical shell

假设射流的冲击速度为100m／s，冲击圆台半径分别为1.0和1.5m，射流长度为1m，圆柱壳的Mises应力响应云图的计算结果如图6所示。初始冲击时刻只在冲击区域附近应力较大，应力峰值达到了333MPa；在t＝4ms时刻，Mises应力的最大值有所减小，但是影响范围增加，应力最大值出现在水柱冲击的边缘，水柱冲击处出现塑性应变；在t＝10ms时刻，水柱冲击的影响范围增大，在t＝20ms时刻，水柱冲击影响至圆柱壳大部分区域，形成永久塑性变形。

水柱冲击加筋圆柱壳的载荷曲线如图7（a）所示，水柱冲击会在结构上产生一个很高的峰值压力，压力峰值为145.6MPa，然后这个压力很快衰减到很小，但是水柱冲击具有明显的方向性。冲击区域中心点的Mises应力时历曲线如图8（a）所示，在冲击过程中，Mises应力在很短的时间内达到峰值，在6ms左右Mises应力迅速下降，随后在90MPa附近波动。冲击区域中心塑性应变曲线如图8（b）所示，圆柱壳在射流冲击载荷下产生了明显的永久塑性变形，达到0.0334。

图6 加筋圆柱壳在射流冲击下的应力云图Fig.6 Mises contour distributed on stiffened cylindrical shell under jet impact

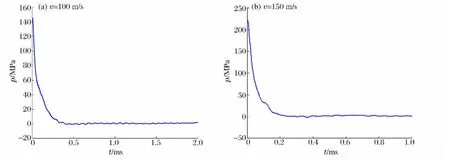
图7 水柱冲击结构的冲击载荷曲线Fig.7 Pressure curve of liquid jet on structure

图8 冲击区域中点Mises应力和塑性应变曲线Fig.8 Mises stress and plastic strain curves of the middle point in impact zone

图9 冲击区域中点Mises应力和塑性应变曲线Fig.9 Mises stress and plastic strain curves of the middle point in impact zone

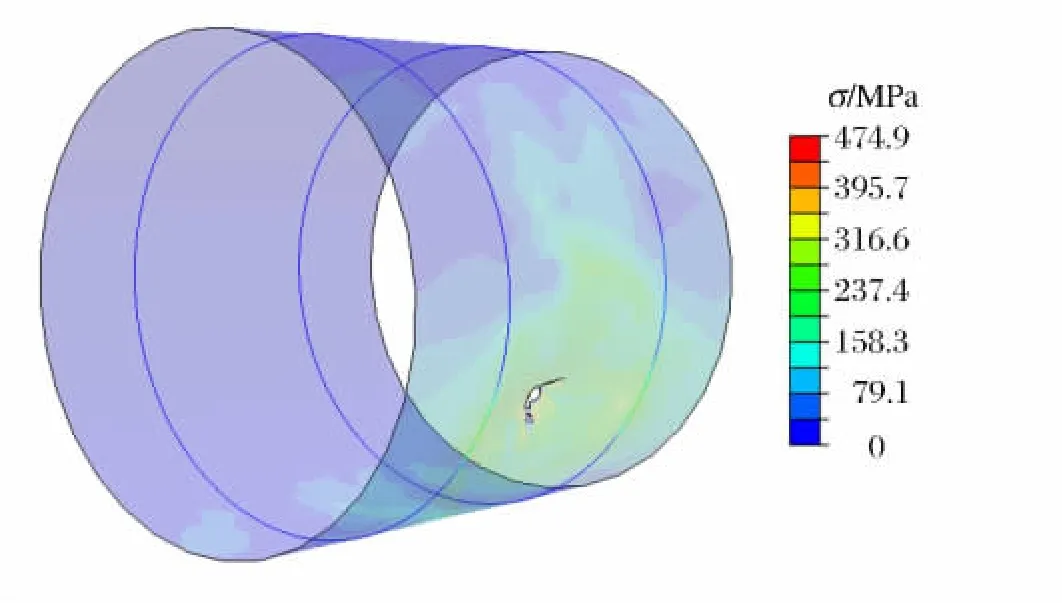
图10 圆柱壳在水柱冲击下产生的破口Fig.10 Crevasse generated by cylindrical shell under jet impact

假设加筋圆柱壳厚度为10mm，气泡射流的冲击速度为150m／s，冲击圆台半径分别为1.0和1.5m，射流长度为1m。水柱冲击加筋圆柱壳的载荷曲线如图7（b）所示，水柱冲击会在结构上产生一个很高的峰值压力，高达223.6MPa，然后这个压力很快衰减到很小。冲击区域中心点的Mises应力曲线如图9（a）所示，在冲击过程中，Mises应力在很短的时间内达到峰值，在6ms左右 Mises应力迅速下降，材料失效后Mises应力为零。冲击区域中心的塑性应变曲线如图9（b）所示，在t＝2.277ms时刻圆柱壳塑性应变到达0.25，材料失效。圆柱壳在射流冲击载荷下产生了明显的永久塑性变形，同时由于塑性应变高于材料的剪切失效值，在射流与圆柱壳作用的中心区域产生破口，破口直径为0.3m，破口如图10所示。

3 结 论

药包在水中结构附近爆炸时会产生直接朝向结构的射流，该射流会对结构产生严重的局部破坏。本文中首先采用线性叠加的方法估算了不同药量、不同水深条件下水下爆炸气泡产生直接作用在圆柱壳表面射流的距离范围，发现：（1）等药量条件下，圆柱壳上部受水深影响较小，下部受水深影响较大，水深越深，影响范围越小，这种影响范围随着药量的减小而减小；（2）等水深条件下，药量越大，影响范围越大，这种影响范围随着水深的增加而减小。最后针对近距离水下爆炸气泡射流载荷计算问题，采用圆台形水柱冲击结构模型进行了简化，并运用DAA方法和有限元软件Abaqus联合求解水柱冲击破坏问题，水下加筋圆柱壳在150m／s水柱冲击作用下产生了破口，对近距离水下爆炸射流载荷问题进行了初步的探索。

［1］Cole R H.Underwater explosion［M］.New Jersey：Princeton University Press，1948：118－127.

［2］Geers T L，Hunter K S.An integrated wave－effects model for an underwater explosion bubble［J］.Journal of the Acoustical Society of America，2002，111（4）：1584－1601.

［3］Klaseboer E，Hung K C，Wang C，et al.Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient／rigid structure［J］.Journal of Fluid Mechanics，2005，537：387－413.

［4］刘建湖.舰船非接触水下爆炸动力学理论与应用［D］.无锡：中国船舶科学技术研究所，2002：89－112.

［5］宗智，何亮，孙龙泉.水下爆炸气泡对水面舰船载荷的数值研究［J］.船舶力学，2008，12（5）：733－739.Zong Zhi，He Liang，Sun Long－quan.Numerical study of loading on the surface ship near an underwater explosion bubble［J］.Journal of Ship Mechanics，2008，12（5）：733－739.

［6］李国华，李玉节，张效慈，等.舰船设备冲击环境的能源研究［J］.船舶力学，1998，2（1）：37－54.Li Guo－hua，Li Yu－jie，Zhang Xiao－ci，et al.Study of power source for shock environment of ship equipment［J］.Journal of Ship Mechanics，1998，2（1）：37－54.

［7］Brett J M，Yiannakopolous G.A Study of explosive effects in close proximity to a submerged cylinder［J］.International Journal of Impact Engineering，2008，35：206－225.

［8］Hung C F，Lin B J，Hwang－Fuu J J，et al.Dynamic response of cylindrical shell structures subjects to underwater explosion［J］.Ocean Engineering，2009，36：564－577.

［9］张阿漫，姚熊亮.水下爆炸气泡与复杂弹塑性结构的相互作用研究［J］.应用数学与力学，2008，29（1）：81－92.Zhang A－man，Yao Xiong－liang.Interaction of underwater explosion bubble with complex elastic－plastic structure［J］.Applied Mathematic and Mechanics，2008，29（1）：81－92.

［10］Wang C，Khoo B C.An indirect boundary element method for three－dimensional explosion bubbles［J］.Journal of Computational Physics，2004，194：451－480.

［11］Zhang Y L，Yeo K S，Khoo B C，et al.3Djet impact and toroidal bubbles［J］.Journal of Computational Physics，2001，166（2）：336－360.

［12］Geers T L.Doubly asymptotic approximations for transient motions of submerged structures［J］.The Journal of the Acoustical Society of America，1987，64：1500－1508.

［13］Huang Y C，Hammitt F G，Mitchell T M.Note on shock－wave velocity in high－speed liquid－solid impact［J］.Journal of Applied Physics，1973，44（4）：1868－1869.