双层楔形爆炸反应装甲飞板的运动规律＊

姬 龙，黄正祥，顾晓辉

（南京理工大学智能弹药国防重点学科实验室，江苏 南京 210094）

ERA自问世以来，成为装甲防护的主要手段。ERA对侵彻体的干扰作用主要来自夹层炸药爆炸产生的高温高压气体、飞板的相对运动和破片等。在上述因素中，飞板飞离弹轴线所需的时间是评定ERA性能优劣的重要标准，飞离时间越长，对侵彻体干扰能力越强［1］。目前，对单层ERA作用机理的研究较多，如M.Held［2－3］就ERA干扰机理进行了深入的研究，对飞板与聚能射流和动能弹的相互作用进行了详细的阐述；S.H.Paik等［4］通过数值模拟和实验，对金属飞板与长杆弹的相互作用过程进行了研究；M.Mayseless［5］就ERA结构参数对防护作用效果的影响进行了详细的论述。此外，还有学者对ERA飞板运动规律也做了相关研究，如M.Held［6］基于动量定理，给出了非对称夹层飞板极限速度的工程计算公式；吴成等［7］采用数值模拟对一代ERA起爆后各飞板的运动规律进行了研究；甄金朋等［8］、刘宏伟等［9］应用数值模拟分析了不同结构参数下ERA飞板的运动规律；沈晓军等［10］对双层“夹层炸药”爆炸后薄板的飞散速度进行了工程计算。综上所述，可见对单层ERA研究较全面，而对双层ERA的研究较少，且主要是利用数值模拟进行分析，还没有一种理论模型能够准确描述双层楔形ERA各飞板的运动规律。

本文中结合工程需要，从单层ERA飞板运动规律，建立双层楔形ERA飞板运动模型，计算出飞板飞离弹轴线所需时间，并通过脉冲X光实验验证理论模型的正确性。

1 理论模型

ERA主要以“三明治”型的平板装药结构为主，即炸药夹层被封闭在2块薄板中间，待炸药爆炸时驱动金属飞板沿其法线方向飞散。双层ERA由2个基本“三明治”单元按一定的结构复合组成，主要有双层平行和双层楔形2种。

侵彻体与双层ERA作用过程，如图1所示。侵彻体穿过上层ERA结构引爆夹层中的炸药，使爆轰产物驱动Ⅰ板、Ⅱ板运动；剩余侵彻体继续运动，继而引爆下层ERA结构夹层中炸药，驱动Ⅲ板、Ⅳ板运动。在Ⅱ、Ⅲ板碰撞前，2个单元相互独立，可按2个ERA先后与侵彻体相互作用进行研究；当发生碰撞后，Ⅱ、Ⅲ板在2组爆轰产物的共同作用下继续运动，最终飞离弹轴线。

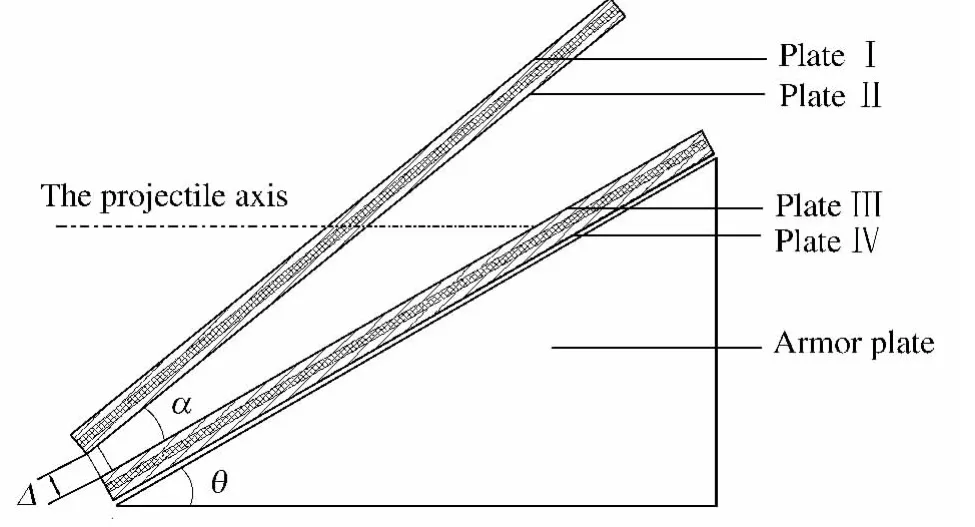
图1 双层ERA放置示意图Fig.1 Schematic diagram of double－layer ERA

1.1 基本假设

ERA的作用过程涉及到炸药爆轰、飞板运动、飞板碰撞和变形等，其过程非常复杂，为了着重考虑各飞板在爆轰产物作用下的运动规律，现做如下假设：（1）ERA结构中的夹层炸药瞬时爆轰，飞板上各点的速度相同，方向垂直于初始板表面，且不考虑板的碎裂；（2）由于爆炸产物压力在膨胀阶段远大于飞板的重力和空气阻力，所以在此只考虑爆轰压力；（3）在飞板加速到极限速度后，由于继续飞行时间极短，所以不考虑速度衰减，以此速度稳定飞行；（4）双层ERA被引爆后，Ⅱ、Ⅲ板发生完全塑性碰撞，且碰撞瞬时完成，共同飞离弹轴线。

1.2 ERA作用规律

ERA结构中的夹层炸药引爆后，在爆轰产物的驱动下，飞板沿其法线方向作背向运动。根据爆轰产物压力的变化，将爆轰产物膨胀过程划分为2个阶段［11］：

绝热膨胀阶段，任意时刻爆轰产物的压力pi为

等熵膨胀阶段，任意时刻爆轰产物的压力pi为

式中：ph、vh分别为夹层炸药瞬时爆轰后的初始压力和比容，瞬时爆轰压力是C－J条件下压力的一半；pk、vk分别为临界压力和临界比容，vi为任意时刻爆轰产物的比容，γ为质量热容比，κ为等熵指数。

结合任意时刻飞板速度微分方程

和炸药瞬时爆轰后飞板位移微分方程

可求得不同时刻飞板运动的变化规律。式中：Si为飞板的受力面积，mi为飞板质量；下标i飞板编号。

1.3 双层平行ERA飞板的运动规律

Ⅱ、Ⅲ板碰撞前，上、下2个ERA单元可看作是相互独立的；待Ⅱ、Ⅲ板碰撞后，Ⅰ、Ⅳ板继续按单个ERA作用规律进行分析，而对Ⅱ、Ⅲ板碰撞瞬间现做如下分析：Ⅱ、Ⅲ板发生正碰撞并焊接在一起，由动量定理得碰撞后两板的共同速度为［10］

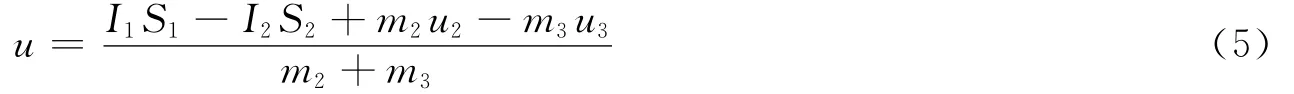
式中：I1、I2、S1、S2分别为上、下层ERA爆轰气体对2块碰撞飞板的比冲量和作用面积。

Ⅱ、Ⅲ板碰撞后仍受到上、下层爆轰产物的共同作用，作用力为

式中：p12、p23分别为上、下层爆炸产物对Ⅱ、Ⅲ板的作用力。

结合ERA作用规律，可以得出双层平行ERA各飞板的运动规律。

1.4 双层楔形ERA飞板的运动规律

双层楔形ERA作用过程与双层平行ERA基本类似，只是双层楔形ERA的上、下层“三明治”互成一定角度，使得上层爆轰产物气体的膨胀方向和飞板运动方向较下层不同，如图2所示。

Ⅱ、Ⅲ板发生斜碰撞，由动量定理和动量矩定理得

图2 Ⅱ、Ⅲ板碰撞示意图Fig.2 Schematic diagram of the collision between flying plateⅡ and flying plateⅢ

式中：un、ut为碰撞后速度u 在n－n 和t－t方向上的分量，α为双层ERA之间夹角即楔形角，J为Ⅱ、Ⅲ板碰撞粘结后的转动惯量，Ω为Ⅱ、Ⅲ板碰撞粘结后所获得的转动角速度，l为反应装甲的长度。

由式（7）～（9）可求得碰撞后Ⅱ、Ⅲ板法线方向速度un、切线方向速度ut以及Ⅱ、Ⅲ板角速度Ω，同时结合双层平行ERA飞板的运动规律，可以求得双层楔形ERA各飞板的运动规律。

2 计算分析

ERA基本单元采用平板炸药夹层结构，其中夹层炸药选用B炸药，密度为1.68g／cm3，爆速为7 840m／s；装甲板倾角θ为30°。双层平行放置时2个单元中间间隔Δ＝20mm，下层ERA较上层延时8μs起爆；双层楔形放置时α＝9°，间隔Δ＝10mm，下层ERA较上层延时11μs起爆。分别对单层、双层平行以及双层楔形ERA各飞板的运动规律进行研究。

图3所示为利用上述理论模型计算得到的单层ERA与装甲板间隔一定距离放置时各飞板的速度时程曲线，所示的飞板速度为装甲板法线方向上的速度分量。从图3中可以看出双板具有类似的运动规律，在任意时刻两板的速度大小相同，方向相反。图4所示为单层ERA紧贴装甲板放置时各飞板的速度时程曲线。由于Ⅱ板紧贴装甲板，所以速度一直为零，Ⅰ板极限速度较图3中增加了38%，且加速时间加长。可以得出：单层ERA放置方式能有效影响各飞板的运动规律。对于单层ERA，飞板大约在20μs内完成加速过程，并保持极限速度飞离作用场；对于双层ERA，飞板在30μs内达到极限速度，并以此速度飞离作用场。

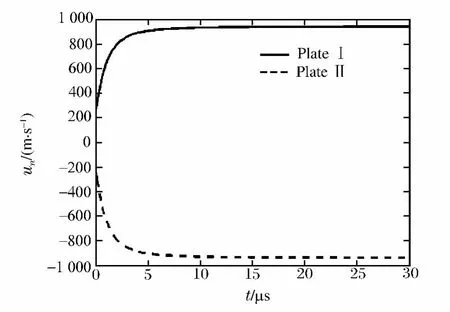
图3 ERA与装甲板间隔一定距离时飞板的运动规律Fig.3 The flying plate’s motion rule at a distance between ERA and armor plate

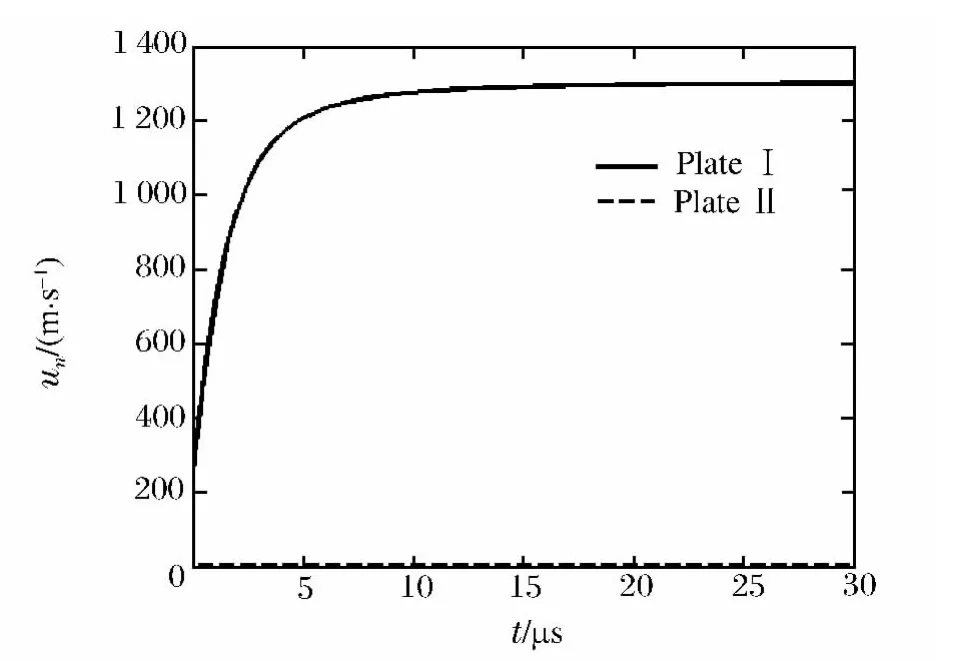
图4 ERA紧贴装甲板放置时飞板的运动规律Fig.4 The flying plate’s motion rule when ERA attached to armor plate

图5～6所示为计算得到的双层平行以及双层楔形ERA中各飞板运动速度。

由图5可知，Ⅱ、Ⅲ板碰撞前，上层ERA飞板的运动规律与图3中相同，而下层ERA与装甲板紧贴，其运动规律与图4中相同。在夹层炸药爆炸后15μs左右，Ⅱ、Ⅲ板发生正碰撞，之后Ⅱ、Ⅲ板粘接在一起沿远离装甲板方向继续运动，且在25μs左右达到最大速度；Ⅱ、Ⅲ板碰撞后向上运动压缩上层爆轰产物，使得Ⅰ板持续加速，极限速度较图3中增加了4.4%。

图6所示为双层楔形ERA各飞板速度时程曲线。Ⅱ、Ⅲ板碰撞前，由于上层ERA与装甲板之间存在夹角，在夹层炸药爆炸后，Ⅰ、Ⅱ板运动方向与装甲板法向存在夹角，故与图3中飞板运动规律不同。下层ERA与装甲板紧贴，其飞板的运动规律与图4中相同。在夹层炸药爆炸后13μs左右，Ⅱ、Ⅲ板发生斜碰撞，碰撞后两板焊接在一起，由于下层ERA较上层延时11μs起爆，使得下层爆轰产物压力远高于上层，所以Ⅱ、Ⅲ板碰撞结束后沿远离装甲板方向加速运动，25μs左右达到最大速度，此速度较图5中Ⅱ、Ⅲ板合速度降低了20%，同时获得角速度Ω＝1.14rad／s。碰撞后Ⅱ、Ⅲ板向上运动压缩上层爆轰产物，使得Ⅰ板速度略有增加。角度效应能够明显影响飞板碰撞后各飞板的运动规律。

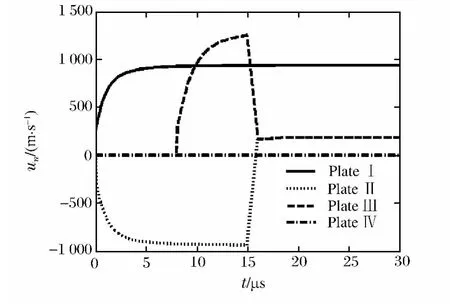
图5 双层平行ERA各飞板运动规律Fig.5 Each flying plate’s motion rule of the double－layer parallel ERA

图6 双层楔形ERA各飞板运动规律Fig.6 Each flying plate’s motion rule of the double－layer wedged ERA

3 实验验证

为了获得双层楔形ERA作用场的规律，实验先从单层ERA各个飞板的运动规律进行研究，通过调整脉冲X光机不同的出光时间得到飞板运动规律的最佳呈现状态，然后通过将单层ERA做垂直于侵彻体方向的实验，获得单层ERA不同放置条件下各飞板的平均运动速度。在此基础上，对双层ERA进行研究，从而获得双层楔形ERA各飞板的运动规律。

3.1 测试方法

实验采用2台脉冲X光射线管布设成45°汇交，聚能装药以垂直方式布设，保证成形后经过2台X射线管汇交轴。通过设置2个脉冲X光机不同的出光时间，1次实验可得到2张不同时刻的X光照片。为了精确测得ERA飞板的飞散速度，实验中还需进行起爆同步设置和参考标记设置。

3.2 实验布局及结构单元

实验采用∅56mm无壳聚能装药，炸高为80mm，采用8＃电雷管起爆。由于只研究飞板的运动规律，聚能装药与ERA垂直布设。实验中ERA单元由上下层钢板以及夹层炸药组成。上、下层靶板材质为45钢，尺寸为250mm×250mm×3mm；夹层炸药选用军用B炸药，用螺栓紧固于双层钢板之间。实验装置示意图如图7所示。

3.3 实验结果及分析

实验中设置2台脉冲X光机出光时间间隔为70μs，由此可以测出各飞板在某个时间段内的平均速度。图8为单层ERA与装甲板间隔一定距离时，所得70、140μs时X光照片；图9为双层楔形ERA在60、130μs时X光照片。

表1所示为不同放置条件和组合方式下，实验结果与理论计算结果的对比，其中计算值均为飞板达到极限速度后，稳定飞行的速度值，δ表示理论计算与实验测量值的误差。

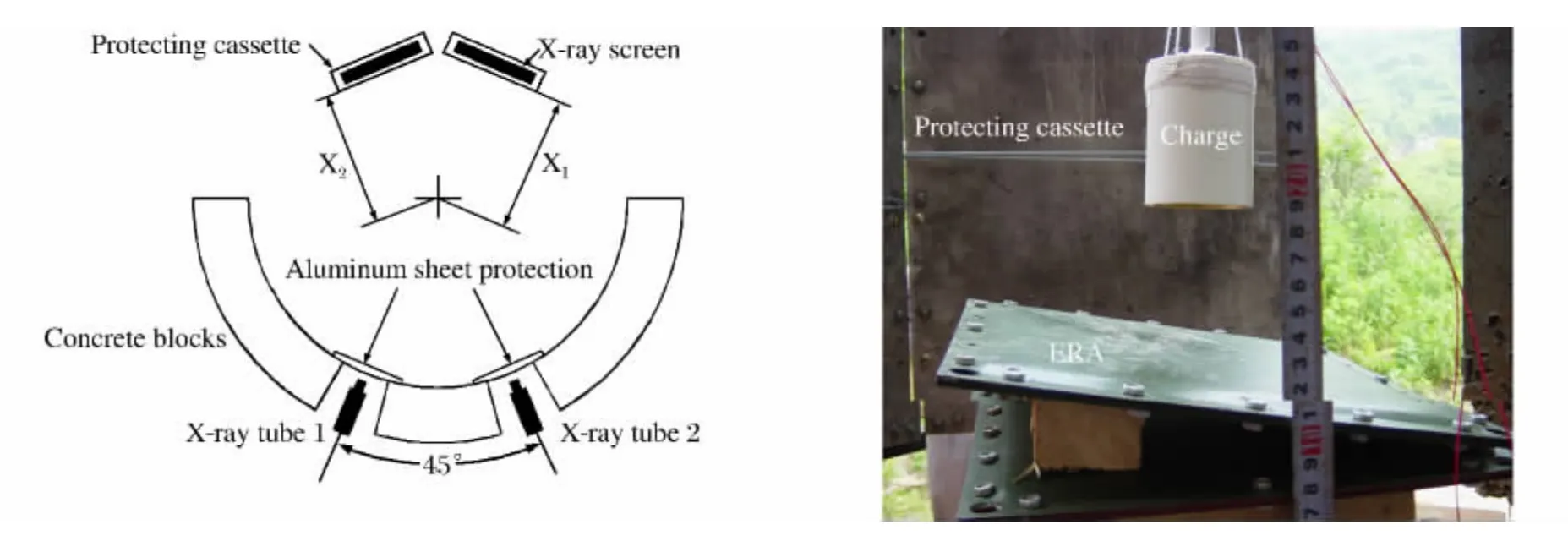
图7 实验布局示意图Fig.7 Schematic of experimental layout

图8 单层ERA脉冲X光照片Fig.8 The flash x－ray photos of single－layer ERA

图9 双层楔形ERA脉冲X光照片Fig.9 The flash x－ray photos of double－layer wedged ERA

表1 飞板运动速度的计算值与实验数据比较Table1 Comparison of the flying plate velocity between calculated value and experimental data

由表1可知，将飞板运动速度的理论计算值与实验值进行对比，单层ERA在不同放置条件下，两者误差较小，均在4%以内；双层ERA2种不同放置方式误差较单层偏大，但误差仍控制在10%以内，满足工程计算要求。

单层ERA与装甲板间隔一定距离时，实验测得Ⅰ、Ⅱ板的速度大小不同，上飞板速度偏低，而理论计算得Ⅰ、Ⅱ板速度大小相同。产生这种误差的原因在于：理论计算忽略了飞板的重力和空气阻力，且没有考虑螺栓的影响；Ⅱ板碎裂变形，造成数据处理存在一定误差。

双层平行和双层楔形ERA中，Ⅰ、Ⅳ板的实验值与理论计算值误差在4.5%以内，而Ⅱ、Ⅲ板误差相对较大。这主要是因为：实验中Ⅱ、Ⅲ板的碰撞过程相当复杂，而理论模型中Ⅱ、Ⅲ板按照完全塑性碰撞处理，较难反映碰撞时的真实状态。然而Ⅱ、Ⅲ板的计算值与实验值的误差均控制在10%以内，满足工程计算要求。此外，理论计算速度为整块板的平均速度，而实验过程中所得速度为板上某点的速度值，导致实验结果与理论计算结果产生一定差异。

4 ERA的作用场时间

通过上述理论计算和实验可以得到单层ERA、双层平行和双层楔形ERA各飞板的稳定飞行速度，由此可以推算出各飞板飞离弹轴线所需时间，即飞板相互作用时间。

图10 不同条件下的作用时间的理论计算和实验结果对比Fig.10 Comparison between theory and experiment of action time under different conditions

图10所示为ERA不同放置条件和组合方式下，飞板飞离弹轴线所需时间的计算结果：类型Ⅰ指单层ERA紧贴装甲板放置，类型Ⅱ为单层ERA与装甲板间隔一定距离放置。其余为双层平行ERA下层紧贴装甲板放置和双层楔形ERA下层紧贴装甲板放置。由图10可知，单层ERA紧贴于装甲板放置时，飞板飞离弹轴线所需时间最短；双层ERA比单层ERA的飞板相互作用时间增加了5倍以上；双层楔形ERA的飞板相互作用时间比双层平行ERA的提高了38%。对比理论计算值和实验结果得：两者误差均在7%以内，满足工程计算要求。此结果也表明，通过飞板的运动速度计算得到的飞板相互作用时间是可靠的，同时也证明了飞板运动规律模型的准确性。

5 结 论

（1）由单层ERA各飞板运动规律的研究着手，通过对双层ERA作用过程进行分析，建立了双层ERA各飞板的运动规律模型，并利用脉冲X光实验进行验证，所得理论计算结果与实验吻合较好，且满足工程计算要求。

（2）运用理论模型，分析了单层、双层平行和双层楔形ERA各飞板的运动规律，进而计算飞板飞离弹轴线所需时间即飞板相互作用时间，结果表明：双层平行ERA的飞板相互作用时间较单层的提高了5倍以上，且双层楔形ERA的飞板相互作用时间又较双层平行ERA的提升了38%。

（3）单层ERA的飞板相互作用时间与ERA和装甲板的相对放置距离有关，间隔放置可以使其有显著的提高。

［1］黄正祥，李刚，陈惠武.双层反应装甲作用场参数数值模拟与实验研究［J］.弹道学报，2005，17（4）：40－43.Huang Zheng－xiang，Li Gang，Chen Hui－wu.Numerical simulation and experimental study on double explosive reactive armor［J］.Journal of ballistics，2005，17（4）：40－43.

［2］Held M.Comparison of explosive reactive armour against different threat levels［J］.Propellants Explosives Pyrotechnics，1999，24：76－77.

［3］Held M.Momentum theory of explosive reactive armours［J］.Propellants Explosives Pyrotechnics，2001，26：91－96.

［4］Paik S H，Kim S J，Yoo Y H，et al.Protection performance of dual flying oblique plates against a yawed long－rod penetrator［J］.International Journal of Impact Engineering，2007，34：1413－1422.

［5］Mayseless M.Effectiveness of explosive reactive armor［J］.Journal of Applied Mechanics，2011，78（5）：1－11.

［6］Held M.Plate velocities for asymmetric sandwiches［J］.Propellants Explosives Pyrotechnics，1997，22：218－220.

［7］吴成，蒋建伟，冯顺山.爆炸反应装甲运动规律的数值仿真及研究［J］.兵工学报，2002，23（1）：35－38.Wu Cheng，Jiang Jian－wei，Feng Shun－shan.A study on the moving features of explosive reactive armor by numerical simulation and experiments［J］.Acta Armamentarii，2002，23（1）：35－38.

［8］甄金朋，刘天生，张硕，等.爆炸反应装甲驱动飞板运动的数值模拟［J］.火炸药学报，2010，33（2）：78－81.Zhen Jin－peng，Liu Tian－sheng，Zhang Shuo，et al.Numerical simulation of the flyer plate propelled by explosive reactive armor［J］.Chinese Journal of Explosives ＆ Propellants，2010，33（2）：78－81.

［9］刘宏伟，夏松林，赵靖，等.反应装甲结构参数对飞板运动影响［J］.兵器材料科学与工程，2011，34（5）：41－43.Liu Hong－wei，Xia Song－lin，Zhao Jing，et al.Influence of the structure parameter of ERA on the moving of flyingpanel［J］.Ordnance material science and engineering，2011，34（5）：41－43.

［10］沈晓军，马晓青，曾凡君，等.双层反应装甲爆炸后薄板飞散速度工程计算［J］.北京理工大学学报，1994，14（4）：341－346.Shen Xiao－jun，Ma Xiao－qing，Zeng Fan－jun，et al.Theoretical calculation of explosive driven metallic plates for two layered sandwiches［J］.Journal of Beijing Institute of Technology，1994，14（4）：341－346.

［11］恽寿榕，赵衡阳.爆炸力学［M］.北京：国防工业出版社，2005：1－122.