电磁膨胀环实验设计的关键因素＊

种 涛，赵剑衡，谭福利，王桂吉，罗斌强

（中国工程物理研究院流体物理研究所，四川 绵阳 621999）

膨胀环加载技术作为实现一维拉应力、高应变率加载的重要实验手段，在材料动态拉伸下失稳、颈缩致热、拉剪断裂、碎裂及本构关系等问题的研究中发挥着重要作用。膨胀环加载主要有炸药驱动和电磁驱动2种方式。利用柱状炸药外爆压力驱动，可达到103以上的应变率，且试样环升温小，缺点是一维应力区域很容易被干扰，且实验重复性较差。电磁加载技术以洛伦兹力为驱动，没有机械力作用产生的波效应，由于加载的均匀性与感应电流的均匀性相关，因此可通过加载电流波形进行调节，对实验参数的控制更加方便。相对爆炸膨胀环，电磁加载也更加安全、简易，便于在实验室完成，可重复性好。

F.L.Niordson［1］首先发展了电磁膨胀环装置，并对铜和铝在常温下进行了单轴拉伸试验，观测到了碎片的产生；W.H.Gourdin［2－3］进一步完善了电磁膨胀环驱动技术，并对试样环的运动进行了简单的电磁学分析；S.V.Serikov［4］对爆炸膨胀环的稳定性进了分析；丰树平等［5］首先对电磁膨胀环技术进行了分析，桂毓林等［6－7］利用此实验技术进行了一些物理实验；汤铁钢等［8］用数值模拟分析了爆炸膨胀环的截面尺寸效应。P.L.Eplattenier等［9］首先利用LS－DYNA对这一过程进行了完整的模拟，但他的工作更多的是侧重于证明磁流体程序在这方面应用的可行性。I.Henchi［10］等对电磁膨胀环进行了二维模拟，运用于材料本构关系的拟合。总的来看，电磁膨胀环加载技术实验较多，但缺乏对整个加载过程的定量认识，从而导致对膨胀环的设计较多依赖于经验。电磁膨胀环的加载过程牵涉到电、热、力的耦合，需要可靠的磁流体的数值模拟，而国外这方面的工作公布很少。本文中利用带有电磁模块的LSDYNA三维动力学有限元程序对电磁膨胀环实验行了力学、热学和电磁学耦合数值模拟，分析实验设计中螺线圈绕法、截面尺寸、加载电流波形、膨胀环宽度等关键因素的影响，讨论膨胀环在螺线圈缺口连接处附近的轴向位移对应力分布的影响，为电磁膨胀环的设计和材料力学实验提供指导。

1 计算模型与材料参数

电磁膨胀环计算模型如图1所示。螺线圈由高电导率的铜线绕制，每匝为带缺口的平面圆环，外径40mm，线截面尺寸为1.5mm×1.5mm，线间距为1.8mm，绕线匝数为6，相邻2个线圈在缺口处连接，每个缺口对应的圆心角为20°，铜的材料参数，密度ρ＝8 490kg／m3，质量热容c＝383J／（kg·K），热导率λ＝398W／（m·K），电导率γ＝6.0×107S／m，弹性模量E＝97GPa，泊松比ν＝0.31。膨胀环材料为M态的TU 1无氧铜，平均半径为21.1mm，截面尺寸为1.0mm×1.0mm；其力学本构模型选择带有应变强化、应变率敏感和温度软化效应的J－C模型［9］，模型的本构参数为，ρ＝892kg／m3，质量热容c＝383J／（kg·K），弹性模量E＝120GPa，泊松比ν＝0.34；常数A＝90，B＝292，N＝0.31，C＝0.025，m＝1.09，热学和电磁学参量和螺线圈材料相同。

螺线圈共512个单元，膨胀环共7 200个单元。由于实验中螺线圈封装固定，因此计算时对螺线圈进行位移约束。计算中螺线圈和试样环升温较小，材料电导率变化不大，所以电导率采用固定值。

采用的LS－DYNA三维动力学有限元程序［10］有电磁学、力学和热学3个求解模块，在进行电磁、力和热耦合问题数值模拟时，每个计算时间步长内先根据材料模型和电磁学参数以及加载条件求解，得到电磁参量；然后分别通过洛伦兹力方程和焦耳热方程，计算每个节点和单元的受力和增加的热量，将洛伦兹力以输入条件传送给力学模块，进行力学计算，将焦耳热以热源条件传递给热学模块进行计算。

对W.H.Gourdin［2］的电磁膨胀环实验进行模拟，验证计算程序和方法的可靠性。膨胀环的感应电流和径向速度计算与实验结果对比见图2，加载阶段的感应电流和自由膨胀阶段的径向速度计算值与实测值最大误差均小于1%。

图1 电磁膨胀环计算模型Fig.1 Computational model for electromagnetic expanding ring

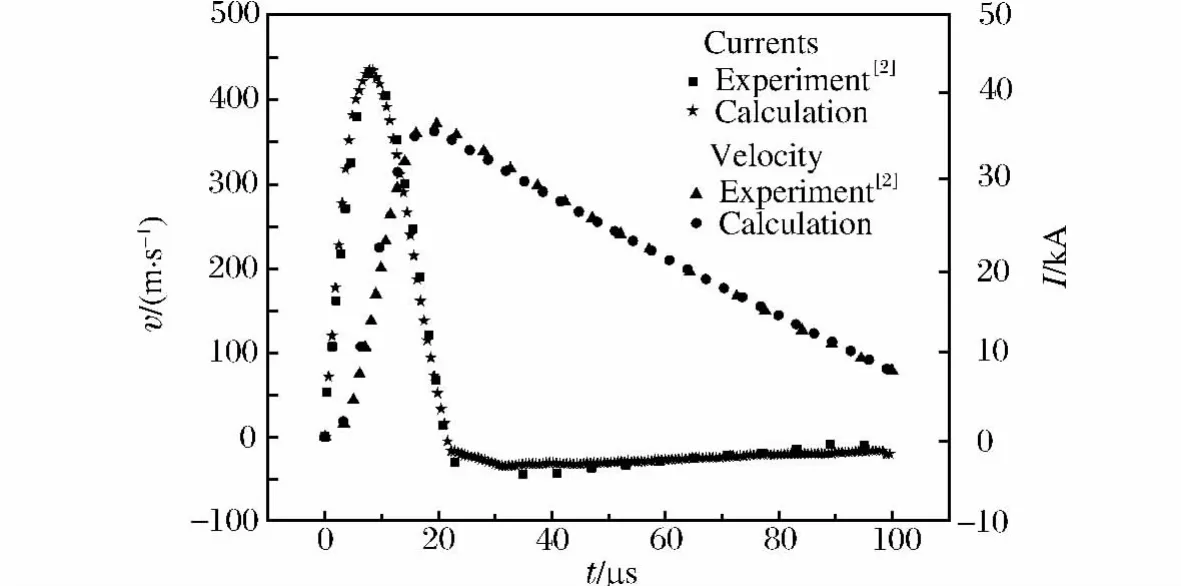
图2 电磁膨胀环中感应电流和径向速度Fig.2 Induced current and radial velocity in electromagnetic expanding ring

2 实验设计关键因素分析

2.1 螺线圈绕法、尺寸

螺线圈绕线方法主要有均匀过渡和带缺口圆圈上下连接2种方式。依照文献［10］建立均匀过渡模型进行计算，结果表明由于线圈倾斜产生的横向磁场会造成膨胀环两侧受到相反的轴向洛伦兹力，膨胀环产生轴向偏转，如图3（a）所示。所以不建议将此绕线方法用于实验。

采用带缺口圆圈上下连接模型，如图1所示。模拟结果表明，膨胀环远离连接处一侧（背面）保持轴向不变形，而靠近连接处一侧（正面）出现了轴向小变形，如图3（b）所示。相比之下，这种绕线方法更加合理，这也是目前大多数电磁膨胀环实验中螺线圈的绕线方法。

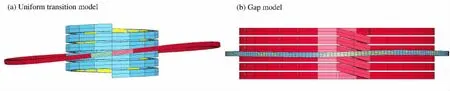
图3 螺线圈模型Fig.3 Coil model

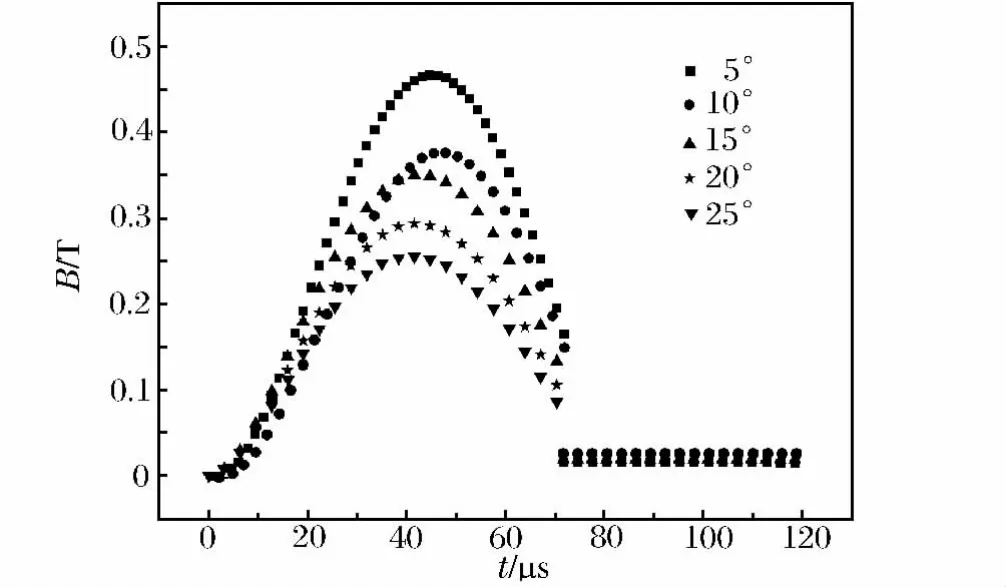
图4 不同缺口圆心角的螺线圈外侧横向磁场对比Fig.4 Comparison of transverse magnetic fields outside the coils with different central angles

线圈缺口的大小、相邻2个螺线圈的中心线间距等因素会直接影响电磁膨胀环实验。以每个圆圈缺口对应的圆心角来表征缺口大小，分别计算5°、10°、15°、20°和25°缺口模型，加载电流为峰值7.5kA，半周期72μs的半正弦波。图4所示为不同缺口大小情况下，在连接处的横向磁感应强度大小，可以看到，缺口越小，产生的横向磁感应强度越大，在电磁膨胀环实验中横向磁场是一个干扰项，应尽量减小；计算得膨胀环正面的径向速度随着缺口的增大而减小，25°连接情况下径向速度最大值比5°情况下减小8.1%左右，而膨胀环背面径向速度5种情况下均相差不到1%，所以连接处的大小会影响膨胀环径向的均匀变形。

当相邻2个螺线圈的中心线间距分别为1.8、2.7和3.6mm的情况下。计算表明，随着间距的增加，膨胀环的轴向位移明显增加，径向速度大幅度减小，如图5所示，说明螺线圈的加载能力下降。分别计算膨胀环和螺线圈之间距离为0.3、0.6、0.9、1.5和2.0mm的情况下，膨胀环径向速度峰值与膨胀环和螺线圈之间距离大小成近似线性关系，比例系数非常接近。

此外，计算外径分别为30、40、50和60mm的螺线圈的模型，在相邻2个螺线圈的中心线间距、截面尺寸，以及膨胀环的截面尺寸、膨胀环和螺线圈之间距离等其他条件均不变的情况下，加载电流均为半周期36μs，峰值22.5kA的半正弦波。图6所示为不同绕成匝后不同直径的螺线圈所对应的膨胀环的径向速度曲线，其中v1、v2分别为背面和正面的径向速度，最后1条曲线为60mm直径，连接缺口处圆心角为5°时正面膨胀环径向速度曲线，随着螺线圈直径的增加，膨胀环的径向速度峰值也明显增加；膨胀环背面和正面的速度相差越来越大，说明膨胀环径向变形不均匀更加严重；直径为60mm时，随着连接处缺口所对应的圆心角减小，膨胀环正反两侧速度差越来越小，圆心角5°时基本可以忽略。

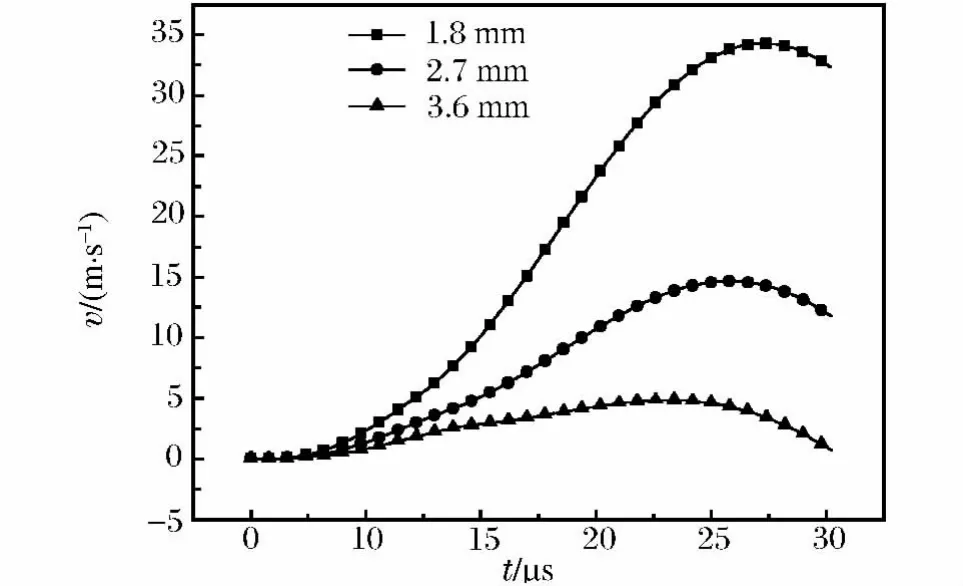
图5 不同的膨胀环与螺线圈距离下膨胀环径向速度对比Fig.5 Comparison of different radial velocities of rings at different clearances

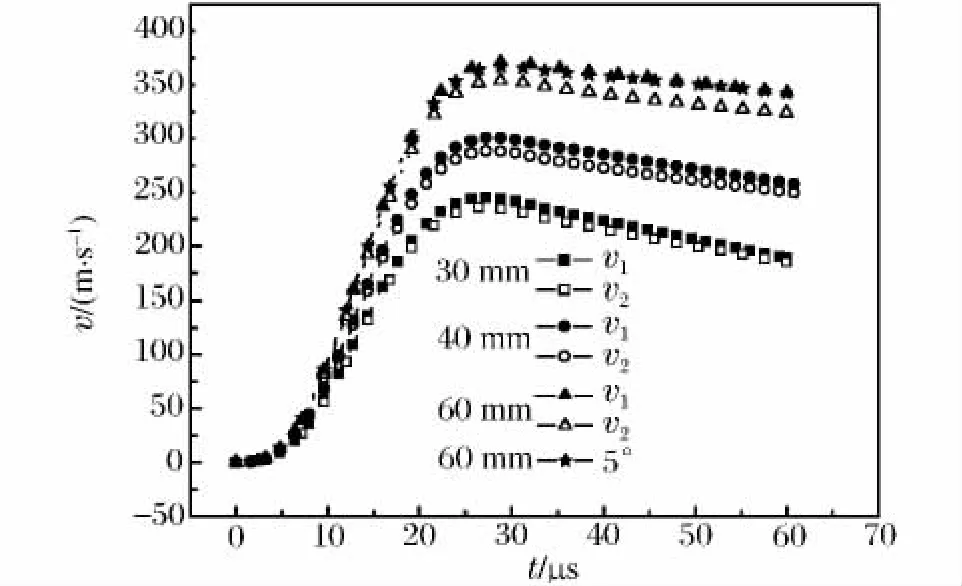
图6 不同螺线圈缺口中心角的膨胀环的径向速度对比Fig.6 Comparison of different radial velocities of rings under coils with different central angles

综上所述，螺线圈缺口处所对应的圆心角的大小随着其外径的增加而减小，对于40mm外径的螺线圈，建议选择15°圆心角，对于60mm外径的螺线圈，建议选择5°圆心角；在保证绝缘的前提下，适当减小相邻2个螺线圈的中心线间距，既可以减小膨胀环的轴向位移，还能增加螺线圈的加载能力。

2.2 加载电流波形

电磁膨胀环实验的加载电流都类似半正弦波，因此主要讨论半正弦波加载电流峰值和上升时间的影响。加载电流分为2组：电流峰值分别为7.5、11.25、15.0、22.5kA，1／4周期均为36μs。电流1／4周期分别为18、24、30、36和54μs，峰值均为7.5kA。

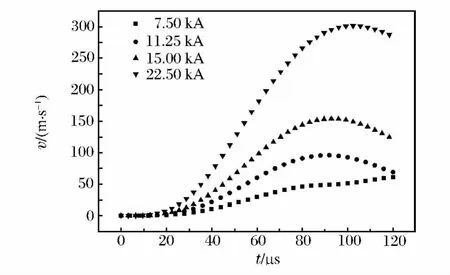
图7 不同电流峰值下的径向速度对比Fig.7 Comparison of different radial velocities at the different current peaks

随着电流峰值的提高，膨胀环径向速度明显的增大，并都在加载电流到达峰值后约6μs时达到峰值，如图7所示。对速度峰值和对应的电流峰值数据进行拟合，较好的符合线性关系。不同峰值加载电流情况下，实验过程中膨胀环的应变率，如图8所示，其趋势与径向速度曲线相似，最大加载应变率与加载电流峰值也成近似线性关系，斜率为603.5。改变加载电流峰值可以对试样环进行不同应变率、不同物理状态加载的实验研究。在提高加载电流峰值的同时需要注意膨胀环在缺口连接处附近的最大轴向位移，当电流峰值为22.5kA时，膨胀环已经有了1倍于自身宽度的轴向位移，如图9所示。

图8 不同电流峰值下膨胀环应变率对比Fig.8 Comparison of strain rates of the ring at the different current peaks

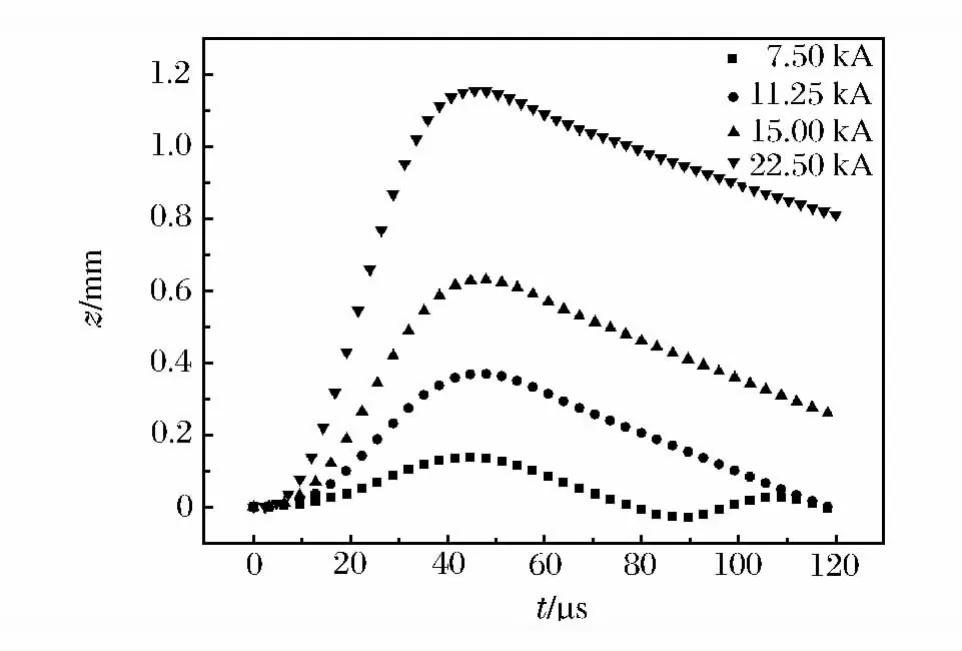
图9 不同电流峰值下的最大轴向位移对比Fig.9 Comparison of the maximum axial displacements of the ring at the different current peaks

当加载电流上升时间不同时，在18～36μs之间，膨胀环的径向速度峰值基本不变，只是到达峰值时间变长；在加载54μs时，速度峰值有所下降，如图10所示。在确定加载的电流强度后，可以适当的改变加载电流上升时间，即对膨胀环的径向速度进行调节。当加载电流峰值不变时，只改变电流的上升时间时，膨胀环的最高温度在各种情况下均约为50℃，且在电流截止后不会再升温。只改变电流峰值时，膨胀环的温度大幅度的增加，且在电流截止后，还会存在温升，图11所示。

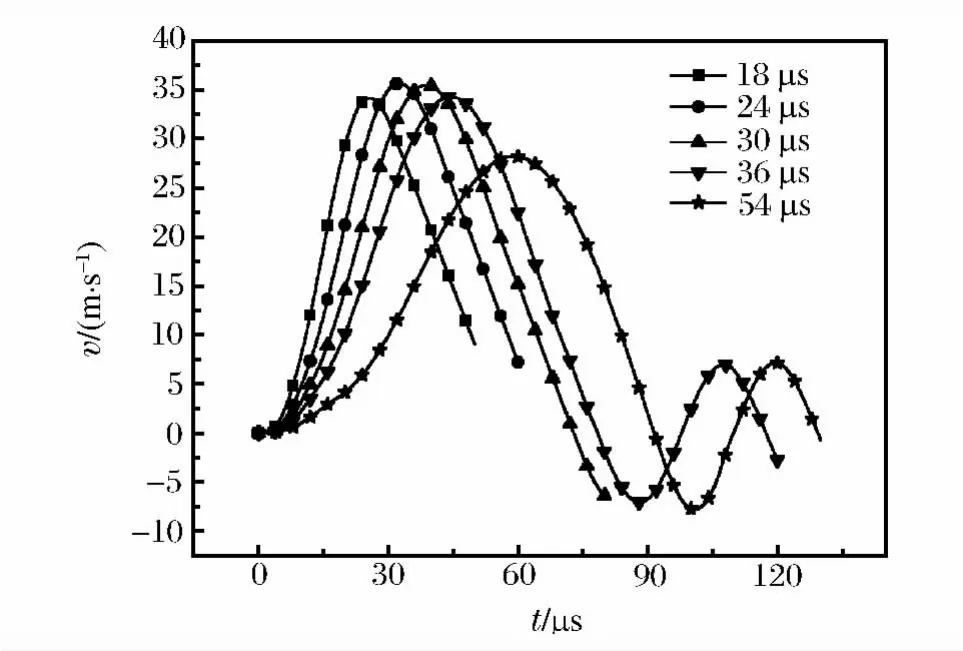
图10 不同上升时间时加载电流的径向速度对比Fig.10 Comparison of radial velocities of the ring at the different rise times

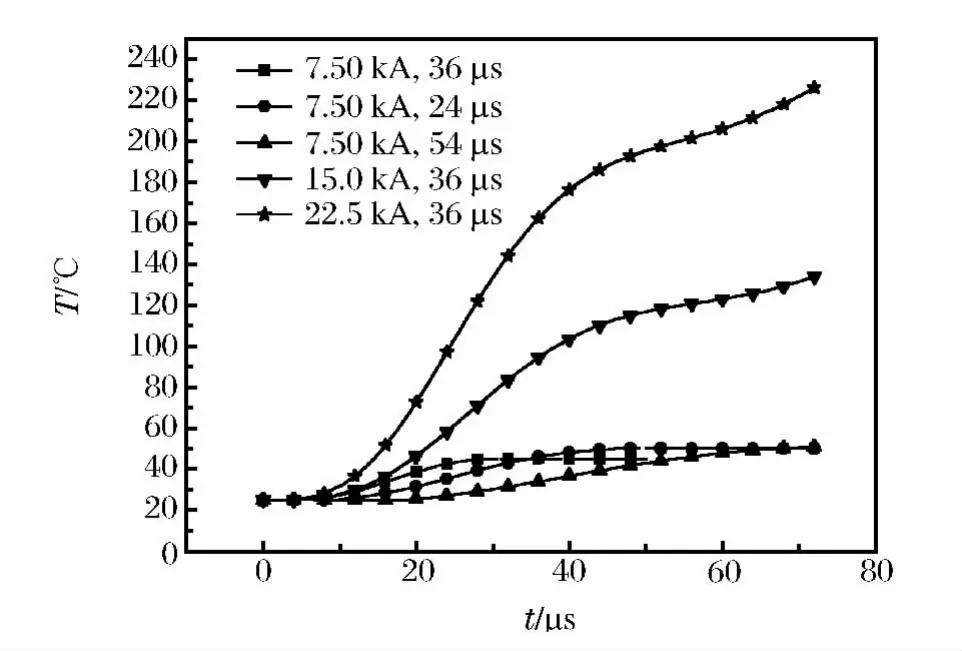
图11 不同电流峰值下的膨胀环温度对比Fig.11 Comparison of temperatures of the ring at the different current peaks

2.3 膨胀环截面沿轴向的宽度

分别计算了膨胀环截面沿轴向的宽度为1、2、4和6mm时的膨胀环模型，膨胀环截面沿径向的宽度均为1mm。为了使计算结果对比更加明显，这里采用上升时间18μs，峰值22.5kA半正弦波作为加载电流。首先考察膨胀环轴向宽度对径向速度的影响。在相同的爆炸驱动条件下，增加膨胀环截面沿轴向宽度可以减小边界稀疏波的影响，提高能量利用率，进而增加径向速度峰值；电磁驱动正好相反，由于螺线圈附近轴向的磁感应强度为中间大、两边小的梯度分布［8］，所以增加膨胀环宽度反而减小径向速度。爆炸膨胀环截面沿轴向宽度为1～8mm，径向速度为约80～100m／s［7］；电磁膨胀环轴向宽度为1～4mm时，速度约从300m／s下降到140m／s，变化更加明显，如图12所示。膨胀环的最大轴向位移随着膨胀环轴向宽度的增加而迅速减小，如图13所示。适当的增加膨胀环轴向宽度，对膨胀环的稳定运动有着良好的作用，但需要注意磁场轴向分布不均匀，会造成加载不均匀。

图12 不同截面沿轴向宽度膨胀环中径向速度对比Fig.12 Comparison of radial velocities of the ring at the different widths of the ring

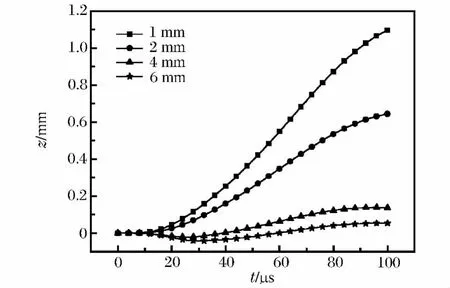
图13 不同截面沿轴向宽度膨胀环中最大轴向位移对比Fig.13 Comparison of the maximum axial displacements at the different widths of the ring

考察膨胀环轴向宽度对环中应力状态的影响，设置1、2、4、6mm等4种情况。膨胀环的自由膨胀阶段进行了一维应力假设：忽略膨胀环中的径向和轴向应力，用环向应力代替等效应力。环向应力和等效应力计算结果如图14所示，4种情况下，环向应力和等效应力均在加载结束40μs后基本重合，说明满足一维应力假设，完全可用环向应力来代替等效应力。图15所示为不同宽度情况下径向和轴向应力曲线，在加载阶段，随着截面沿轴向宽度的增加，膨胀环中径向应力不断减小，而轴向应力不断增加；加载完成后，膨胀环径向和轴向应力都很快接近于零，截面沿轴向宽度为6mm膨胀环轴向应力消除需要稍长时间。约50μs后进入自由膨胀阶段，径向和轴向应力均不到环向应力的1%，可以满足一维应力假设。综合考虑加载效率和稳定性，膨胀环截面沿轴向宽度建议选择1～2mm，沿径向宽度为1mm。

图14 不同截面沿轴向宽度膨胀环中环向和等效应力对比Fig.14 Comparison of the effective and hoop stresses at the different widths of the rings

图15 不同截面沿轴向宽度膨胀环中径向和轴向应力对比Fig.15 Comparison of the radial and axial stresses at the different widths of the rings

2.4 膨胀环的轴向位移

由于螺线圈缺口处的斜线连接使得试样环受到轴向的洛伦兹力，试样环会在螺线圈缺口连接一侧产生轴向位移，一边为正，一边为负。轴向位移的存在会产生复杂应力，自由膨胀开始阶段膨胀环轴向应力较大且集中分布在螺线圈连接处附近；随着时间的推移，轴向应力减小，且分散开，而环向应力增大；膨胀环背面一侧应力均匀性始终良好。计算得出轴向位移影响虽然不大，但还是要尽量减少。合理设计螺线圈缺口处大小，可尽量减小相邻2个螺线圈中心线间距，并适当增加膨胀环截面沿轴向宽度。

为了减小轴向位移，提出双螺线圈模型，如图16所示。内外2个螺线圈缺口位置相同，缺口连接方向相反。膨胀环平均半径为21.1mm，截面尺寸为1.0mm×1.0mm，以15.0kA峰值电流同时驱动2个螺线圈，试样环径向速度峰值约330m／s，如图17所示；对于单螺线圈，22.5kA峰值电流驱动相同试样环时径向速度约300m／s，可参考图12将两者轴向位移和轴向应力进行比较。单螺线圈时试样环的最大轴向位移约1.15mm，可参考图12，而双螺线圈时的约为0.17mm，如图17所示；双螺线圈模型与单螺线圈模型情况下，自由膨胀阶段（36μs起）3个不同时刻的环向应力和最大轴向应力见表1。由计算结果知，双螺线圈模型的轴向位移干扰明显减小，但是这种电磁膨胀环还需实验验证。关于膨胀环轴向位移对电磁膨胀环实验具体的影响，还需要进一步研究。

图16 双螺线圈模型Fig.16 Double coil model

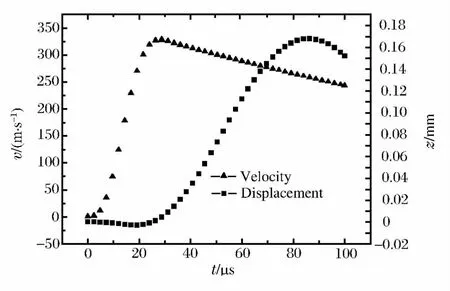
图17 双螺线圈模型的径向速度和轴向位移Fig.17 Radial velocity and axial displacement of the ring with double coil model

表1 膨胀环应力分布Table1 Stress distribution of the ring

3 结 论

利用LS－DYNA三维动力有限元程序对电磁膨胀环加载过程进行了数值模拟，并获得以下结论：

（1）连接带缺口圆圈绕线方法优于均匀过渡绕法，但螺线圈缺口处大小需要针对具体实验模拟设计；螺线圈线间距在保证绝缘的前提下应适当减小。

（2）螺线圈直径增大，其加载能力提高，但膨胀环的最大轴向位移也会增大。

（3）加载电流上升时间相同时，电流峰值与膨胀环径向速度峰值近似成线性关系。

（4）适当增加膨胀环的截面沿轴向宽度，会降低其径向速度峰值，提高膨胀环运动稳定性。

（5）双螺线圈模型可以有效的减小膨胀环轴向位移和轴向应力。

［1］Niordson F L.A unit for testing materials at high－strain－rates［J］.Experimental Mechanics，1965，5（1）：29－32.

［2］Gourdin，W H.Analysis and assessment of electromagnetic ring expansion as a high－strain－rate test［J］.Journal of Applied Physics，1989，65（2）：411－422.

［3］Gourdin W H，Weinland S L，Boling R M.Development of the electromagnetically launched expanding ring as a high－strain－rate test technique［J］.Review on Science Instrument，1989，60（3）：427－432.

［4］Serikov S V.Stability of the flow of metallic rings under the action of an explosion［J］.Translated from Fizika Gorenyai Vzryva，1975，11（1）：112－119.

［5］丰树平，孙承纬.高速电磁自由膨胀环实验技术［C］∥第四界全国冲击动力学学术会议.太原，1994：267－271.

［6］桂毓林，孙承纬，李强，等.实现金属环动态拉伸的电磁加载技术研究［J］.爆炸与冲击，2006，26（6）：481－485.Gui Yu－lin，Sun Cheng－wei，Li Qiang，et al.Experimental studies on dynamic tension of mental ring by electromagnetic loading［J］.Explosion and Shock Waves，2006，26（6）：481－485.

［7］桂毓林.电磁加载下金属膨胀环的动态断裂与碎裂研究［D］.绵阳：中国工程物理研究院，2007.

［8］汤铁钢，李庆忠，刘仓理，等.爆炸膨胀环的截面尺寸效应［J］.爆炸与冲击，2010，30（6）：39－44.Tang Tie－gang，Li Qing－zhong，Liu Cang－li，et al.Size effects of expanding ring by explosive loading［J］.Explosion and Shock Waves，2006，30（6）：39－44.

［9］Eplattenier P L，Cook G，Ashcraft C，et al.Introduction of an electromagnetism module in LS－DYNA for coupled mechanical－thermal－electromagnetic simulations［J］.Steel Research International，2009，80（5）：351－358.

［10］Henchi I，Eplattenier P L，Daehn G，et al.Materials constitutive parameter identification using an electromagnetic ring expansion experiment coupled with LS－DYNA and LS－OPT［C］∥The 10th International LS－DYNA Users Conference Proceeding，2008.