基于数字化再设计方法的船舶航向控制器设计

徐 飞, 刘明雍



基于数字化再设计方法的船舶航向控制器设计

徐 飞, 刘明雍

（西北工业大学航海学院, 陕西西安, 710072）

船舶航向运动系统具有典型的非线性和不确定性, 并容易受到风、浪、流等的干扰。针对船舶航向操纵特点, 给出其非线性系统模型描述, 在包含参数摄动和环境扰动等不确定性条件下推导了基于T-S模糊船舶航向运动的离散化模型。采用数字化再设计方法设计了一种船舶航向数字控制器。运用计算机仿真手段, 将所设计的数字控制器和传统比例-微分-积分(PID)控制器进行对比。仿真结果表明, 基于数字化再设计的船舶航向控制器的动态性能优于传统的PID 控制器。

船舶航向控制器; 数字化再设计; 比例-微分-积分控制

0 引言

船舶航向运动的目的是在安全性和经济性的前提下, 要求船舵能够控制船舶沿着预定的航线航行。一般而言, 船舵是以航向作为控制坐标, 由于船体易受风、浪、流等外界干扰的影响, 无法保证船舶沿着预定的航线航行。而在复杂海情下, 船舶航向和横摇运动之间存在严重的耦合。因此, 船舶航向控制表现为一个复杂的控制问题。由于船舶航向动态系统具有非线性、大滞后、大惯性等特性, 而风、浪、流等干扰的随机性以及航行工况的频繁变化又使船舶运动数学模型呈明显的不确定性。

在船舶非线性离散控制器设计领域, 近年来有研究者提出了滑模控制、控制、反步法、神经网络等控制方法用于船舶航向控制。上述方法很好地处理了船舶动态运动的非线性问题, 但其适应参数变化和环境扰动的能力有限, 而且计算量也比较大, 对于计算机的实时处理要求较高。控制、反步法等对受控对象模型要求较高, 算法相对复杂, 不易被工程设计人员掌握; 神经网络控制的完备性理论未彻底验证, 计算能力有待于进一步研究; 模糊控制的工程设计直观易行, 但控制规则的确定和优化往往还很困难。

数字化再设计是由Shieh等学者提出不确定采样系统控制器设计方法, 其思想是将已设计好的连续控制器转换为等效的离散控制器, 并保持控制器稳定性。利用数字再设计方法进行设计也取得了一些新的研究成果。文献[8]利用T-S(Takagi-Sugeno)模糊模型来解决控制器设计中的不确定性, 但并未给出鲁棒稳定条件。文献[9]中利用近似线性化法来处理非线性不确定扰动的系统鲁棒控制器设计问题, 其假定非线性系统都可以线性化, 有很大的局限性。

本文推导了船舶航向非线性系统模型, 利用数字化再设计方法设计了新型航向控制器, 在包含参数摄动和环境扰动等不确定性条件下对船舶航向鲁棒控制系统进行了仿真研究。

1 基于T-S模糊模型的数字化再设计

假设一般化的船舶航向控制系统动态模型如下

使用中心平均去模糊化方法, 经过系统推理, 则全局TS模糊动态系统可描述为

其中

(3)

, 且(5)

连续T-S模糊状态反馈控制率已经设计好, 用来作为数字化设计控制器的依据。其形式如下

去模糊化的控制器输出

(7)

进一步得

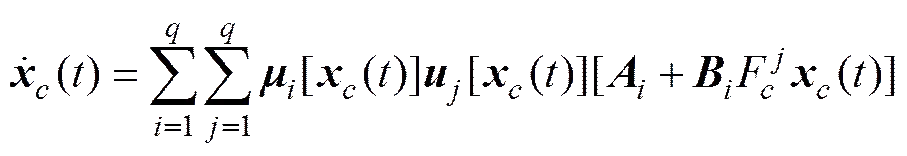
期望的数字控制系统可描述为

(9)

因此, 数字化再设计问题可描述为在离散时间域发现相应的数字控制器满足在每一个采样时刻的状态匹配。

利用前述的离散化理论, 离散化形式为

因此, 数字化再设计模糊控制器采用如下的形式

在采样周期内的全局控制律

(12)

闭环离散系统

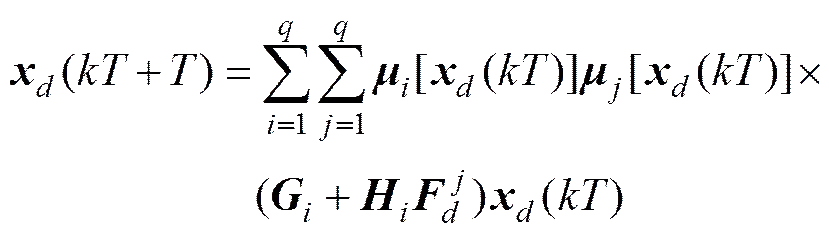
结论1: 所描述的系统可用离散化理论近似离散化

(14)

数字化模糊控制器的状态与已有的模拟模糊控制器闭环T-S模糊系统的全局动态行为匹配, 且保持稳定特性, 其描述如下。

离散化的闭环系统在利亚布诺夫稳定条件下全局指数稳定。

(15)

(16)

利用Schur补充引理, 可以线性矩阵不等式(linear matrix inequality, LMI)的形式表达

(18)

利用LMI, 求得

2 船舶航向运动控制器数字化再设计

船舶航向控制系统数学模型可以用以下状态方程表示

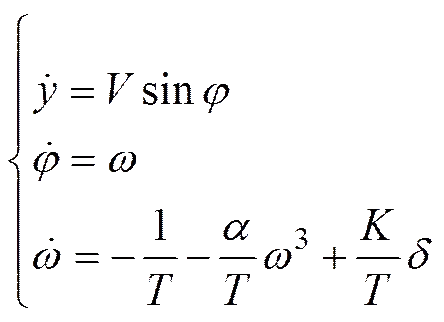
原船舶航迹模型式(1)可表示为如下线性模型

(22)

利用双线性近似法, 当一个采样周期足够小时, 将式(2)连续时间的状态空间模型转换为对应离散时间下的不确定线性系统模型

(24)

即

船舶在航向保持的过程中, 会根据偏航量和偏航量的变化率来调整舵角以操纵船舶的航向。因此, 将航向偏差和作为它的2个前件变量。考虑以船艏为基准, 规定角度逆时针方向为正方向, 将,和控制量的数量范围划分为正大(PB)、正小(PS)、零(Z)、负小(NS)、负大(NB) 5个模糊集,可得航向模糊控制规则, 如表1所示。则输入和的隶属度函数如图1和图2所示。

表1 船舶航向模糊控制规则

3 仿真结果与分析

仿真试验中, 以某作业远洋船为例进行航向控制器设计研究, 该船船长=236 m, 船体宽度=23.6 m, 满载情况吃水深度=7.9 m。通过计算得该船舶运动模型的无量纲参数=7.63,= 12. 9。假设船舶的初始速度为= 6.8 m/s, 船舶运动模型的参数为,/。同样对该远洋船在比例-积分-微分(proportional integrative derivative, PID)控制器下的运动情况进行仿真比较。PID 控制器的设计结论, 可得出自动舵PID 控制参数:,,。取航向角14º, 在采样周期=1.5s下, 仿真结果见图3。同样, 为便于对比, 取改变航向角24°, 在采样周期=2.5 s下, 其仿真结果如图4 所示。

由仿真结果可知, 在航向偏差和偏航量初始条件取值较小的情况下, 采样周期较小时(=1.5 s), 数字化再设计方法中船舶的偏航量及航迹向偏差能够在很短的时间内收敛; 而传统的PID方法中船舶的偏航量及航迹向偏差收敛所用的时间较长。在采样周期较大时(=2.5 s), 传统的PID方法中仿真结果表明, 控制量偏大, 出现发散现象; 而数字化再设计方法中船舶的偏航量及航迹向偏差仍然可以衰减为0(见图3和图4), 使船舶回到设定的航迹向上来。

4 结束语

利用T-S模糊模型的数字化再设计方法的离散控制器设计过程和仿真表明, 此方法得到的离散控制器能够在较短时间内到达稳定, 且较好地完成船舶的航向保持功能。与传统的PID 船舶控制器相比, 船舶航向稳定的过渡时间更短, 超调量更小。可见, 利用数字化再设计方法得到的船舶航向模糊控制器要优于传统的PID控制器。

[1] 赵大威, 边信黔. 非线性船舶动力定位控制器设计[J]. 哈尔滨工程大学学报, 2011, 32(1): 57-61.Zhao Da-wei, Bian Xin-qian. Design of a Nonlinear Controller for Dynamic Ship Positioning[J]. Journal of Harbin Engineering University, 2011, 32(1): 57-61.

[2] Tannuri E A, Pesce C P．Comparing Two Different Contr- ol Algorithms Applied to Dynamic Positionings of a Pipeline Launching Barge[C]//Proceedings of the 10th Mediterranean. Conference on Control and Automation．Lisbon, Portugal, 2002: 297-303.

[3] Katbi M R, Grimble M J, Zhang Y H. Robust Control Design for Dynamic Ship Positioning[J]. Marine Control, IEEE Proc-Control Theory Appl, 1997, 144(2): 110-118.

[4] Fossen T I, Grovlen A．Nonlinear Output Feedback Control of Dynamically Positioned Ships Using Vectorial Ob- server Backstepping[J]. IEEE Transactions on Control Te- chnology, 1998, 6(1): 121-128.

[5] Zhang Y, Hearn G E, Sen P．A Neural Network Approach to Ship Tracking-keeping Control[J]. IEEE Journal of Oc-eanic Engineering, 1995, 20(1): 65-72.

[6] 陈瑜, 殷虎. 基于模糊理论的船舶航向控制器[J]. 舰船电子工程, 2009, 29(13): 83-85.Chen Yu, Yin Hu. A Fuzzy Autopilot for Course-keeping. Ship Electronic Engineering[J].Ship Electronic Engin- eering, 2009, 29(13): 83-85.

[7] Joo Y H, Chen G, Shieh L S. Hybrid State-space Fuzzy Model Based Controller with Dual-rate Sampling for Digital Control of Chaotic Systems[J]. IEEE Transactions on Fuzzy Systems, 1999, 7(2): 394-408.

[8] Wang C, Park J B, Joo Y H. Design of Sampled-data Fuzzy-Model-Based Control Systems by Using Intelligent Digital Redesign[J]. IEEE Transactions on Circuits Sys- tems. 2002, 49(4): 509-517.

[9] Lee H J, Kim H B, Joo Y H. A New Intelligent Digital Re- design for T-S Fuzzy Systems: Global Approach[J]. IEEE Transactions on Fuzzy Systems, 2004, 12(4): 274-284.

[10] 周倩, 宋立忠.基于线性化模型的船舶航迹滑模控制器的设计[J]. 海军工程大学学报, 2009, 19(1): 99-104.Zhou Qian, Song Li-zhong. Design of Sliding Mode Controllers for Ship¢s Track-keeping Control Systems Based on Linearized Models[J]. Journal of Naval University of Engineering, 2009, 19(1): 99-104.

[11] Chang W, Park J B. Joo Y H. GA-Based Intelligent Digital Redesign of Fuzzy-Model-Based Controllers. Fuzzy Systems[J]. IEEE Transactions, 2003, 11(1): 35- 44.

(责任编辑: 杨力军)

Design of Ship Course Controller Based on Digital Redesign Method

XU Fei, LIU Ming-yong

(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

The ship course motion system has typical nonlinearity and uncertainty, and it is sensitive to wind, wave and current interferences. Considering the manipulation features of ship course, this paper presents the description of the nonlinear system model, deduces a discretization model based on Takaigi-Sugeno(TS) fuzzy ship course in the condition of parameter perturbation and environment disturbance, and designs a digital controller of ship course by using digital redesign method. The designed robust controller is compared with the traditional proportional-integral-derivative(PID) controller in dynamic performance by using computer simulation technology. The results show that the present ship course controller performs better than the traditional PID controller.

ship course controller; digital redesign; proportional-integral-derivative control

TJ631.2

A

1673-1948(2013)06-0440-05

2013-04-20;

2013-06-07.

国家自然科学基金(No.51179156); 航空基金(No.2011ZC53043).

徐 飞(1980-), 男, 博士, 讲师, 主要研究方向为数字化再设计, 计算机仿真.