基于PICKETT交会图油气层渗透率计算方法研究

李文湘，王培春，吕洪志，崔云江，张琳琳，陈红兵

（中海石油有限公司天津分公司，天津 300452）

0 引 言

渤海湾盆地的诸多油田中，储量评价阶段的渗透率预测[1－2]往往是直接依靠孔隙度—渗透率二者之间的回归关系，或将粒度中值、孔隙度等参数进行多元回归。这样得到的渗透率不够精确，给后期的开发配产带来了许多问题。自1984年由Hearn[3]首次提出储层流动单元的概念之后，中国的许多学者针对流动单元开展了大量的研究，就各地区的实际情况通过各种方法划分流动单元[4－6]。1990年Hartmann和Coalson[7]以科罗拉多州东南部的索伦托地区Morrow砂岩资料为例提出了以PICKETT交会图划分流动单元的方法，通过研究发现，介于不同饱和度之间的数据在地层垂向上分布不同，孔隙度及渗透率具有各自不同的特征。基于此，根据现有的孔隙度及电阻率测井，可实现流动单元的划分。

本文根据渤海地区的实际情况，结合PICKETT交会图在研究流动单元方面的应用建立了适合该区实际情况的渗透率计算方法，经过实际资料的验证，该方法能够满足油田勘探开发的需要。

1 常规方法计算渗透率存在的问题

渗透率资料主要依靠测井解释、岩心分析和试井资料。岩心分析和试井资料获得的渗透率值虽然准确，但是成本较高，数据点只是全井数据中的很少一部分。在实际油田的勘探评价过程中，渗透率计算的通用方法是建立在岩心孔隙度—渗透率关系的基础上。通过岩心的孔隙度—渗透率的拟合关系，在得到孔隙度的前提下，直接应用二者的拟合关系换算渗透率。

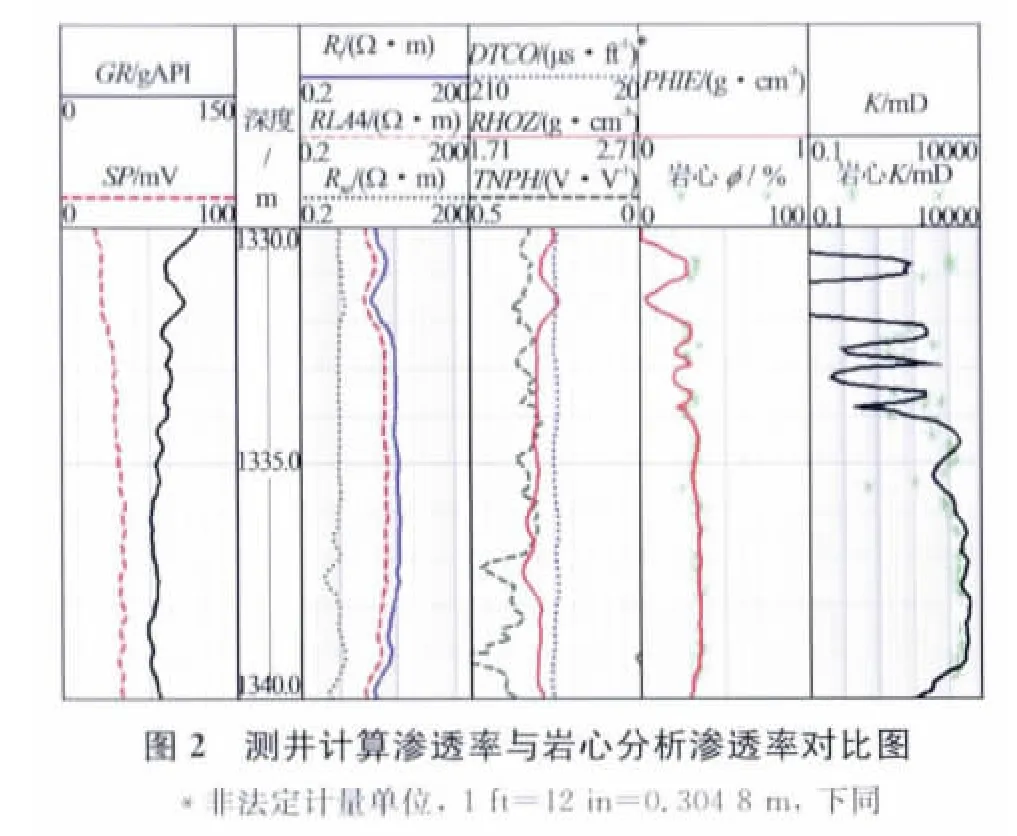
从图1可以看出，利用岩心分析的孔隙度与渗透率关系拟合效果较好，二者之间的相关关系可达0.81。在此关系的基础上计算得到的渗透率与岩心分析得到的渗透率对比分析（见图2）显示效果不是很理想，这说明单纯考虑渗透率与孔隙度的关系计算渗透率不能满足实际需求。这就需要从其他方面着手，多角度分析渗透率预测思路。

2 PICKETT交会图综合应用

2.1 PICKETT交会图的理论基础

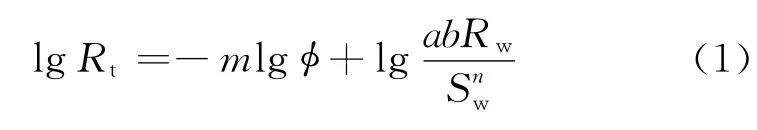
式中，Rt为地层真电阻率，Ω·m；Rw为地层水电阻率，Ω·m；φ为有效孔隙度，%；Sw为含水饱和度，%；a、b为岩性系数；m为胶结指数；n为饱和度指数。

可见，在双对数坐标中，Rt与φ之间关系是一组斜率为－m、截距为lg（abRw／Snw）的直线。对于岩性稳定（a，b，m，n不变）、地层水电阻率Rw稳定的解释井段，直线的截距仅随含水饱和度Sw而变，这就是PICKETT交会图[8]（见图3）。

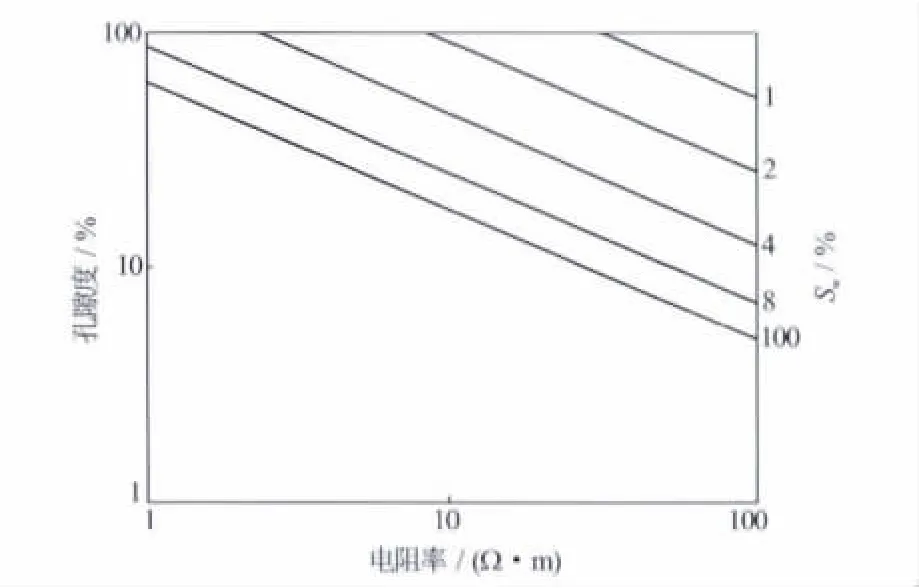
图3 典型PCIKETT交会图

2.2 PICKETT交会图在划分流动单元中的应用

Hearn提出储层流动单元的概念，即为垂向上和横向上连续的、具有相似孔隙度、渗透率和层面特征的储集带[3]。经过近30年的发展，中国的许多学者对流动单元的概念及研究方法进行了丰富和发展，就各地区的实际情况通过各种方法划分流动单元。目前进行流动单元划分应用最多的方法就是流动层带指标法，由修正的Kozeny-Carman方程得到[9]

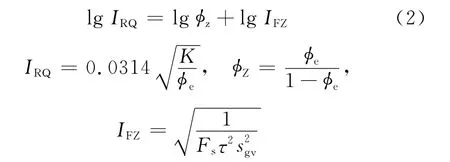
式中，IRQ为储层品质系数，无因次；φz为孔隙与颗粒体积之比，无因次；IFZ为流动层带指标，无因次；K为渗透率，mD；φe为有效孔隙度，%；Fs为形状指数，无因次；τ为迂曲度，无因次；Fsτ2为 Kozeny常数，无因次；sgv为单位体积颗粒的表面积，μm2。

由式（2）可得出，在IRQ与φz的双对数坐标图上，具有相似流动层带指数的样品形成一条斜率为1的直线，不同流动层带指数的样品形成若干条斜率为1的平行直线。Amaefule认为，流动层带指数相同的样品具有相同的孔喉特征，属于同一流动单元。

另外，还有类似多参数储层流动单元划分等诸多方法。通过研究发现，这些方法参数众多，仅仅依靠常规实验和测井曲线在划分流动单元上不确定性很大。Hartmann和Coalson[7]提出了以PICKETT交会图划分流动单元的方法。在PICKETT交会图上，不同截距即不同含水饱和度之间的储层在垂向上分布不同，孔隙度及渗透率具有各自不同的特征，表现出一定的流动单元特征。图4为渤海湾盆地某油田的实际测井曲线。根据上述理论划分储层流动单元。

图4 渤海地区某井各流动单元测井曲线特征

当Sw≤45%时，划为流动单元1，在图4上LDANYU＝1；当45%＜Sw≤70%时，划为流动单元2，在图4上LDANYU＝2；当Sw＞70%时，划为流动单元3，在图4上LDANYU＝3。

3 流动单元法渗透率计算模型的建立

在PICKETT交会图划分完流动单元之后，结合岩心分析数据建立各流动单元渗透率计算模型（见图5）。各流动单元的计算公式如下。

流动单元1

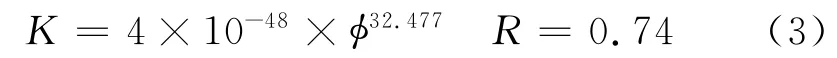
流动单元2

流动单元3

式中，K 为地层渗透率，mD；φ为地层有效孔隙度，%；R为相关系数。把式（3）至式（5）编入测井解释程序，基于PICKETT交会图先对储层进行流动单元的划分，根据不同的流动单元再选择不同的渗透率计算模型。

图5 各流动单元孔隙度—渗透率关系图

4 应用实例

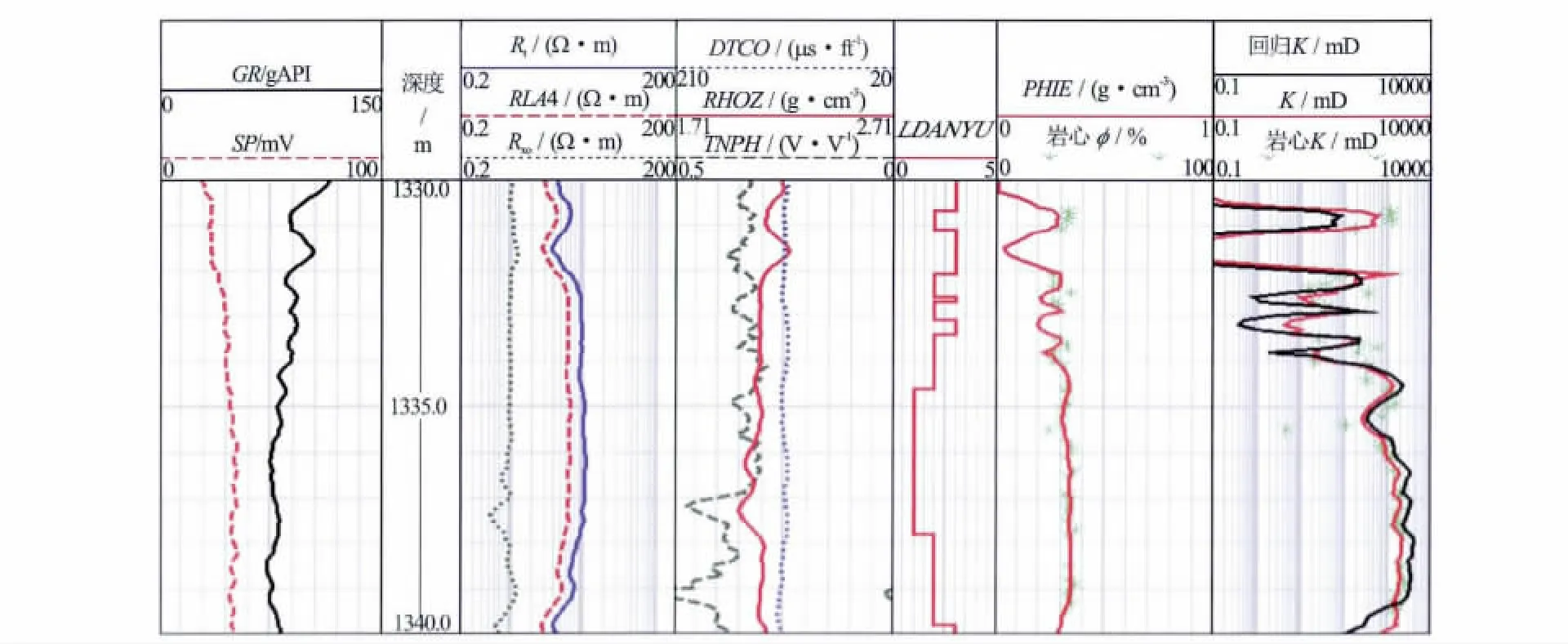
图6 渤海地区A井岩心分析渗透率与预测渗透率对比分析

为验证上述方法的有效性，以渤海某地区某油田的取心井A井为例，对渗透率计算方法进行验证分析（见图6）。A井在1330～1340m段进行了取心，统计分析该井的44块岩心样品渗透率平均值为1024.3mD，对应样品的测井解释渗透率平均值为964.3mD（见图6第7道红线），二者绝对误差为60.0mD，相对误差约5.9%；而原先直接利用孔隙度—渗透率回归关系计算的渗透率平均值仅为835.7mD（见图6第7道黑线），二者绝对误差为188.6mD，相对误差约18.4%。对比分析可见，利用PICKETT交会图先划分流动单元再计算渗透率的思路得到的渗透率较以前有了明显的改善，其预测精度能够满足勘探开发的需要。

5 结 论

（1）基于PICKETT交会图划分流动单元具有很强的实用性，拓宽了PICKETT交会图的应用范围。

（2）对直接利用孔隙度—渗透率回归关系拟合效果不理想的情况，采用PICKETT交会图先划分流动单元再进行油气层的渗透率预测效果明显。

[1]荆万学.常规测井资料计算砂岩储层渗透率的理论思考 [J].测井技术，2002，26（1）：46-48.

[2]贾文玉.渗透率的理论计算方法 [J].测井技术，2000，24（3）：216-219.

[3]Hearn C L，Ebanks W J，Tye R S，et al.GeologicalFactors Influencing Reservoir Performance of the Hartzog Dra Field[J].J Petrol Tech，1984，36：1334-1335.

[4]欧家强，罗明高，王小蓉.低渗透油藏中储层流动单元的划分 [J].西安石油大学学报：自然科学版，2008，23（5）：24-28.

[5]高伟，王允诚，刘宏.流动单元划分方法的讨论与研究 [J].西南石油大学学报：自然科学版，2009，31（6）：37-40.

[6]万丙乾，马玉明，郭晓坤，等.储层流动单元研究现状 [J].天然气勘探与开发，2008，31（1）：5-8.

[7]Hartmann D J，Coalson E B.Evaluation of the Morrow Sandstone in Sorrento Field，Cheyenne County，Colorado[C]∥Sonnenberg S A，et al.Morrow Sandstones of Southeast Colorado and Adjacent Areas，EMAG Symposium，1990：91-110.

[8]Pickett G R.A Review of Current Techniques for Determination of Water Saturation from Logs[J].Journal of Petroleum Technology，1966：1425-1433.

[9]Amaefule J O，Altunbay M，Tiab D，et al.Enhanced Reservoir Description：Using Core and Log Data to I-dentify Hydraulic（Flow）Units and Predict Permeability in Uncored Interval／Wells[J].SPE 26436，1993.