门式起重机运动过程中负载摆动对系统的影响分析

强宝民，赵典

(第二炮兵工程大学，陕西西安710025)

门式起重机作为一种运输机械被广泛应用于港口码头、冶金工业、建筑工程等方面，起重机的小车机构通过柔性钢丝绳与负载相连，导致在大小车加减速或受到外界因素干扰的过程中会引起负载的摆动。负载的摆动不仅大大增加了事故发生的可能性，而且还会造成门式起重机的定位时间过长，严重影响了生产效率。通过对负载摆动的动态过程进行深入的分析，研究负载的摆动过程对系统的影响，为负载的消摆研究和起重机的精确定位研究提供理论依据。

目前，《起重机设计规范》中采用动载荷系数法对起重机整机或小车启制动过程中产生的水平动载荷进行分析，简单地将柔性悬挂的负载与小车机构刚性连接来考虑，忽略了起重机启制动过程中负载的摆动，显然不能满足现代高性能起重机发展的技术要求。文中通过建立起重机运动过程中负载的单自由度系统模型，对系统在启动加速阶段、稳定运行阶段和制动减速阶段负载摆动的动态过程进行了深入的分析。

文中以小车运动过程中负载的摆动为例进行分析，大车运动过程中负载摆动的分析与小车一致。

1 小车在启动加速阶段负载摆动的微分方程

门式起重机的小车机构在启动加速的过程中负载的摆动会对小车产生持续的水平载荷，负载通过钢丝绳与小车机构相连接，不能简单地视为刚性连接处理。针对此问题，首先建立负载摆动的单自由度系统模型［3］，并对模型做以下假设:

(1)负载摆动过程中钢丝绳长度不变;

(2)将负载简化为质点对系统进行分析;

(3)忽略负载摆动过程中的空气阻力对负载的影响。

负载摆动的系统模型如图1所示，假设小车的启动加速时间为t1，稳定运行时间为t2，制动减速时间为t3。

图中m1、m2分别为小车和负载的质量，θ为负载的摆角，F为小车所受驱动力与摩擦阻力的合力，T为钢丝绳的拉力，l为钢丝绳的长度。负载在摆动过程中摆角θ比较小，可近似认为 sinθ≈ θ，cosθ≈1 。

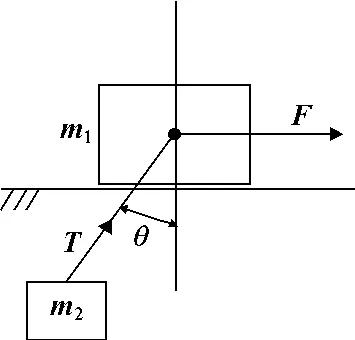
图1 负载摆动单自由度系统模型示意图

设小车与重物的坐标分别为(x，0)、(xm，ym)，则有:

评析： 教学的本质意义是师生和生生之间借助教材文本或探究实验过程中进行的思维对话[2]。“生命的起源”一节教学的能力目标是应用证据和逻辑作出科学的推测。重点在具体事例分析中对生命的起源有一个整体上的认识。因此，通过学生之间对老子“天下万物生于有，有生于无”的思维对话中，可判断A、B、C三位学生能够在事实和逻辑的基础上作出科学合理的推测，并应用抽象与概括形成自己的观点。只有D的认知逻辑错误，因此观点不成立。

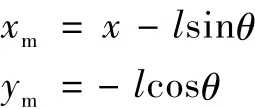
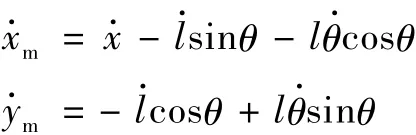
忽略钢丝绳的形变，则上述方程可简化为:

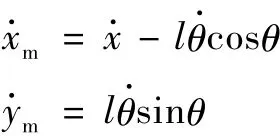
系统的动能为:

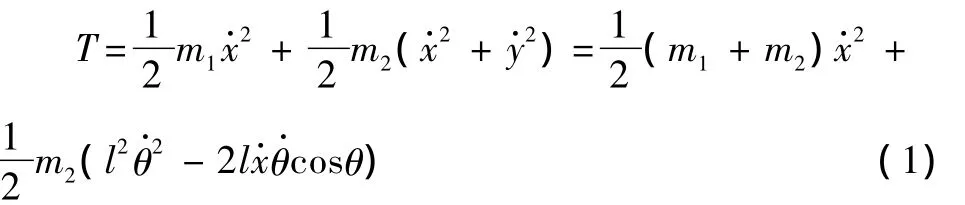
系统的拉格朗日方程［1］为:

将式 (1)分别代入式 (2)、(3)中可得:

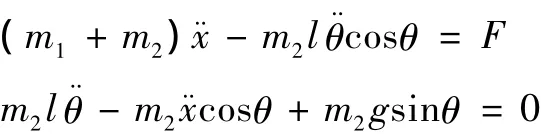
对上式进行化简可得:

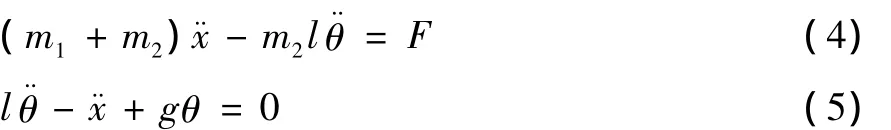
对式 (5)进行Laplace变换可得:

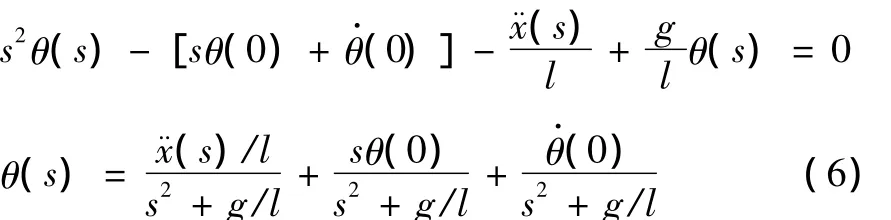
在小车的启动加速阶段，负载由零位置开始摆动，故初始摆角和摆角速度均为零。式 (6)化简为:

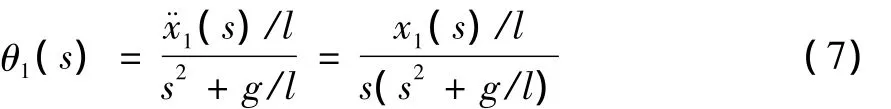
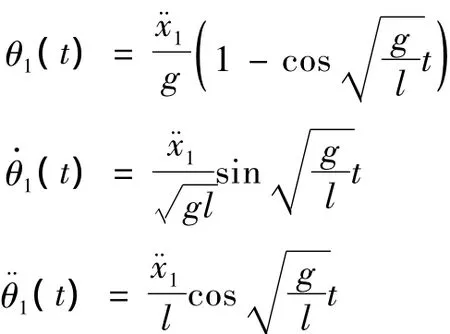
对小车应用牛顿第二定律得:

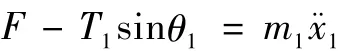
将式 (4)代入上式得负载在摆动过程中对系统水平方向的影响力为:

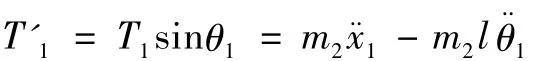
2 小车稳定运行阶段负载的摆动微分方程

假设小车经过时间为t1的加速过程后进入稳定运行阶段，负载进入自由摆动阶段，式 (5)变为:

由式 (8)可得负载在自由摆动阶段的摆角［2］为:

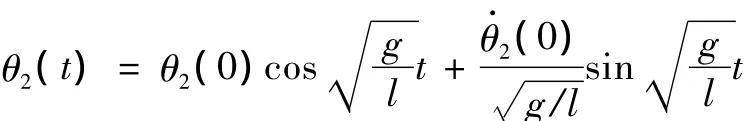
自由摆动阶段的初始值为小车在t1时刻负载的摆角θ(t)和角速度:

11

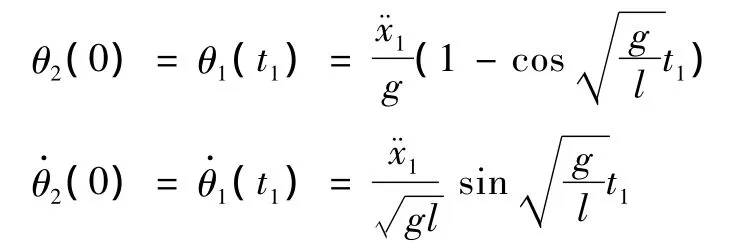
负载的摆角为:

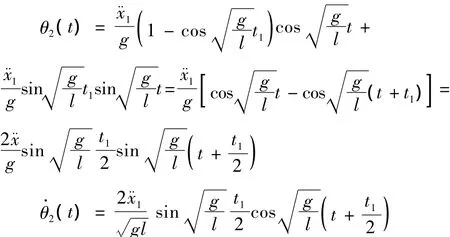
由上式可以看出，负载在自由摆动阶段的最大摆角为:

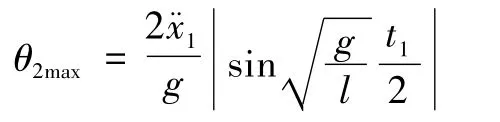
在自由摆动阶段对负载进行受力分析可得:

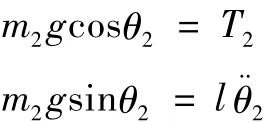
负载在摆动过程中对小车水平方向的影响力为:

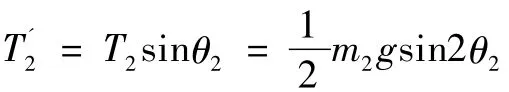
3 小车制动减速阶段负载摆动的微分方程

小车在制动减速阶段的动力学分析与在启动加速阶段相同，但此阶段负载摆动的初始值并不为零，对式 (6)求拉氏反变换可得:

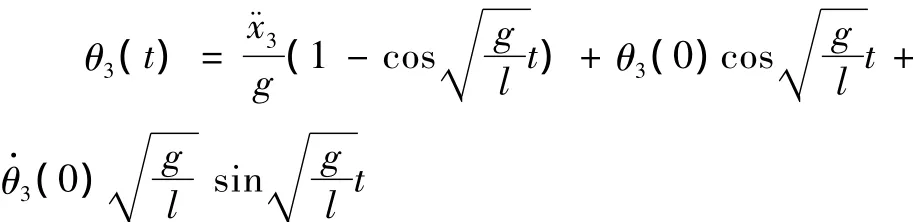
负载摆动的初始值:

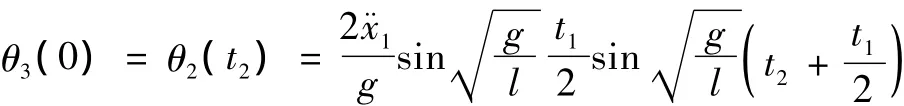
在此阶段，负载在摆动过程中对系统水平方向的影响力为:

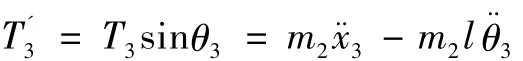
4 系统的仿真分析与实验

根据负载摆动的单自由度系统模型，在MATLAB/Simulink环境中对系统模型进行动力学的建模与仿真。根据试验台的使用规定，设置系统的加速度为0.25 m/s2，最大速度为1.25 m/s。取重力加速度g=9.81 m/s2，钢丝绳的长度l=2.5 m。小车的运动过程分为3个阶段:启动加速阶段、稳定运行阶段和制动减速阶段。

设置小车的运动速度曲线如图2所示。

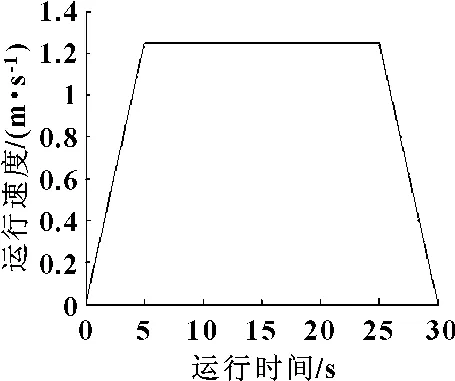
图2 小车的运动速度曲线

负载的摆角在Simulink中的模型如图3所示。

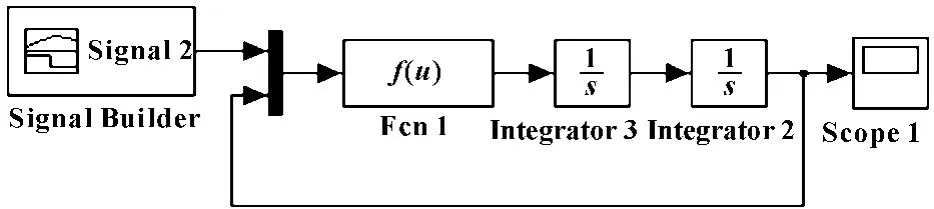
图3 负载摆角的Simulink模型图

负载在运行的整个过程摆角的仿真曲线如图4所示。可以看出:小车在加速时负载随着小车的加速而加速，负载的摆角恒为正值，其平衡位置并非位于零位置;小车在加速阶段结束时负载摆角的大小为在稳定运行阶段负载摆角的峰值，稳定运行阶段负载摆角的平衡位置为零位置，所以适当控制系统的加速时间即可在一定程度上减弱系统在稳定运行阶段负载的摆动程度，同时也减弱了负载摆动对小车带来的水平载荷;系统在稳定运行阶段结束时负载的摆角同样也影响着小车在减速制动阶段负载摆动的程度，从图中可以看出，此阶段负载摆动的平衡位置也不在零位置。

负载在摆动过程中对小车影响的水平载荷的仿真图形如图5所示。可见:小车在各个运行阶段负载的摆动对系统影响的水平载荷呈周期性变化。小车在启动加速阶段，负载始终随着系统的加速而加速，其摆角恒为正值，所以对系统影响的水平载荷也恒为正值;当小车处于稳定加速阶段时，负载以零位置为平衡位置、以加速阶段结束时负载摆角的大小为峰值进行摆动，负载对系统影响的水平载荷的峰值与加速阶段结束时的水平载荷相同;小车处于减速制动阶段时，与启动加速段相比，摆角的表达式中多两项初值项，导致水平载荷比启动加速阶段大，但是两者的周期是相同的。

图4 系统运动过程中负载的摆角的仿真曲线

图5 负载的摆动对系统影响的水平载荷仿真曲线

在实验中，将数据采集卡采集到的实验数据通过Excel文件导出后，导入到MATLAB中，绘制负载的摆动对系统影响的水平载荷的数据曲线如图6所示。可以看出:系统在稳定阶段运行时间较长，在此阶段中，负载受空气阻力的影响，负载摆角的幅值呈衰减趋势，但速度很慢，说明空气阻力对系统的影响较小，基本可以忽略不计。通过水平载荷的仿真曲线和实验结果的对比可知:仿真结果与实验结果基本相同，证明了该理论方法的可行性。

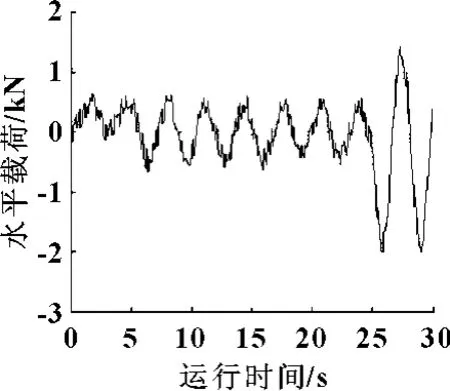
图6 负载的摆动对系统影响的水平载荷实验曲线

5 结论

分析门式起重机运行过程中负载摆动对系统的影响，推导出了在启动加速阶段、稳定运行阶段和制动减速阶段负载摆角的表达式和负载的摆动对系统影响的水平载荷的表达式，在MATLAB/Simulink环境中对系统进行建模仿真，得到了负载的摆角和水平载荷的曲线，通过与实验数据相对比，证明了该理论方法的可行性。

【1】李惠彬．振动理论与工程应用［M］．北京:北京理工大学出版社，2006．

【2】刘延柱，朱本华，杨海兴．理论力学［M］．北京:高等教育出版社，2006．

【3】肖鹏，王冰．基于MEMS微加速度计的无视觉传感器防摇控制系统研究［J］．机电工程，2005(22):1－5．

【4】汪军，沈娇．桥式起重机吊重随小车运行时的摆动仿真［J］．机械研究与应用，2011(6):21 －23．

【5】肖博．柔性悬挂对门式起重机动力响应影响的研究［D］．武汉:武汉理工大学;2010．

【6】陈文，傅蔡安．混合驱动冲压机构的运动学分析及参数优化［J］．机床与液压，2011，39(7):111 －113．

【7】琚鑫，郑鹉．任意振幅摆动周期误差分布的数值计算［J］．物理快报，2011(40):34 －36．