用微分求积法分析轴向加速粘弹性梁的非线性动力学行为*

王冬梅 张伟 刘燕

(1．北京工业大学机电学院，北京 100022)(2．山东济宁学院数学系，曲阜 273155)(3．西华师范大学物电学院，南充 637002)

用微分求积法分析轴向加速粘弹性梁的非线性动力学行为*

王冬梅1，2张伟1†刘燕1，3

(1．北京工业大学机电学院，北京 100022)(2．山东济宁学院数学系，曲阜 273155)(3．西华师范大学物电学院，南充 637002)

用微分求积数值方法求解了轴向加速粘弹性梁的横向振动控制方程，其方程是一复杂的非线性偏微分方程．并在数值结果的基础上利用分叉图分析了轴向定常加速度以及轴向加速度变化幅值对轴向加速粘弹性梁的非线性动力学行为的影响．

非线性偏微分方程， 数值解， 混沌， 分叉， 微分求积法

引言

轴向移动粘弹性梁可以作为多种工程装置的力学模型，比如动力传送带、磁带、带锯、空中缆车索道、高楼升降机缆道、单索架索道等．轴向移动粘弹性梁的非线性动力学性质对工程装置的稳定性和可靠性有着重要的影响．因此分析轴向移动粘弹性梁的横向非线性振动的非线性动力学行为对分析解决工程的实际问题有着重要的意义．轴向移动粘弹性梁的横向非线性振动的控制模型是一非线性偏微分方程．众所周知，只有极少数的偏微分方程有精确解析解，而大多数的偏微分方程是不能得到精确解析解的，尤其是非线性的．为了实际的需要，需寻求近似的方法．很多学者，比如Ravidra和Zhu［1］，Marynowski和 Kapitaniak［2］，杨晓东和陈立群［3］，陈丽华［4］等人，丁虎和陈立群［5］等对轴向移动梁采用伽辽金截断的方法进行了分析．伽辽金截断方法在求解问题时会遇到大量的积分，这无疑会加大计算量．而70年代［6］发展起来的微分求积法是求解偏微分方程的数值计算方法．相对于传统的数值计算方法微分求积法具有原理简单(不依赖于变分原理)计算量小，精度高等优点70年代末在工程领域得到迅速发展和应用．

纵观微分求积法在力学领域的应用，主要是用来静力分析或自由振动分析．将微分求积法用于长时间历程的非线性动力学性质分析的还很少．本文利用微分求积法对陈丽华［4］等人建立的轴向加速粘弹性梁的横向振动的控制方程进行了数值求解，并在数值结果的基础上对其非线性动力学性质比如分叉、混沌等进行了分析．

1 控制方程

陈丽华［3］等人利用哈密顿原理建立的轴向加速粘弹性梁的横向振动的控制方程为:

边界条件为:

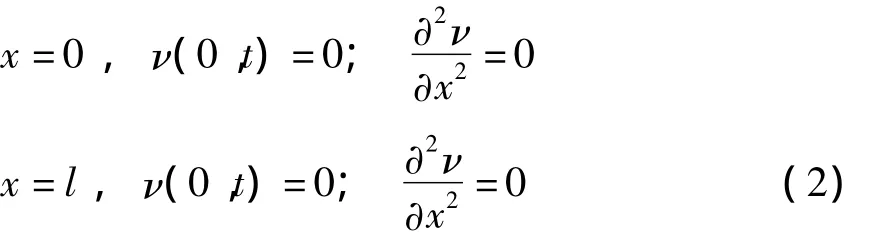
其中:ρ为密度，A是截面积，l是梁的长度，ν(x，t)表示轴向空间坐标x处，t时刻的面内振动的横向位移，η是粘弹系数，E是杨氏模量，Jy是惯性力矩．假定在预紧力P0处有一小的扰动P1sinωt，也就是说紧力P=P0+P1sinωt;假定轴向运动的速度是简谐变化的，也就是c=c0+c1sinωt．这种假设是有它的物理意义的．比如，当我们用轴向移动梁来模拟一对转动轮上的带时，轮子转动时的扰动，会引起带轴向移动速度的扰动．

2 微分求积法的应用

微分求积法的基本原理是将函数在求解区域内的每个网格点处的导数值用域内全部网格点上的函数值的加权线性和近似表示．将其代入原方程，会得到含有网格点上未知函数值的代数方程组．从而微分方程的求解转化为代数方程组的求解．依照微分求积法原理，引入N个网格点:

方程(1)中未知函数的各阶偏导数在各网点的值可以表示为

其中一阶权系数及相应的高阶权系数分别为:

将(4)(5)代入方程(1)以及边界条件(2)并应用权系数修正法［6］得到:

其中:νj= νj(x，t)．(6)式是一常微分方程组，用龙格库塔算法对其求解．

3 数值结果

在以上数值结果的基础上利用分叉图考察了轴向定常加速度和轴向加速度变化幅值对轴向加速粘弹性梁的非线性动力学性质的影响．以下图中都取

3．1 轴向定常加速度的影响

图1是定常加速度c0在区间［15，16．5］变化，轴向加速度变化幅值c1=3．75时的分叉图．从图1中我们可以发现，运动由c0=15开始时是2倍周期的，随着c0的增大出现一个很大的混沌窗口即区间c0∈［15．55，16．2284］，之间出现了多倍周期运动即8倍周期如图6，还出现了一个非常小的4倍周期窗口．之后运动又变为2倍周期的．

图1 轴向定常加速度的影响Fig．1 Effect of mean axial velocity

3．2 轴向加速度变化幅值的影响

图2是定常加速度c0=15．25，轴向加速度变化幅值c1在区间［2，4］上变化时的分叉图．从图3中我们可以发现c1由2变化到大约2．225时，运动是单周期．随着的增大，混沌运动和周期运动窗口交替出现．即由区间［2．225，2．305］－［2．305，2．445］－［2．445，2．795］－［2．795，3．06］－［3．06，3．405］－［3．405，3．725］－［3．725，4］顺序变化时，运动由混沌－周期－混沌－周期－混沌－周期交替变化的．在混沌窗口中出现了10倍周期运动如图8．

图2 轴向加速度变化幅值的影响Fig．2 Effect of amplitude of axial velocity fluctuation

下面图3－8⒜，⒝分别是典型的周期运动和混沌运动的相图以及庞加莱截面．

图3 单倍周期运动:c0=15．25，c1=2，⒜相图⒝庞加莱截面Fig．3 periodic －1 motion appears when c0=15．25，c1=2 ⒜ phase portraits⒝ Poincare maps

图4 2 倍周期运动:c0=15．25，c1=2．29，⒜相图⒝庞加莱截面Fig．4 periodic －2 motion appears when c0=15．25，c1=2．29，⒜ phase portraits ⒝ Poincare maps

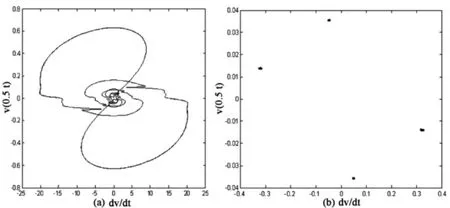
图5 4倍周期运动:c0=16．047，c1=3．75，⒜ 相图 ⒝ 庞加莱截面Fig．5 periodic －4 motion appears when c0=16．047，c1=3．75，⒜ phase portraits⒝ Poincare map

图6 8 倍周期运动:c0=15．81，c1=3．75，⒜相图⒝庞加莱截面Fig．6 periodic －8 motion appears when c0=15．81，c1=3．75，⒜ phase portraits ⒝ Poincare map

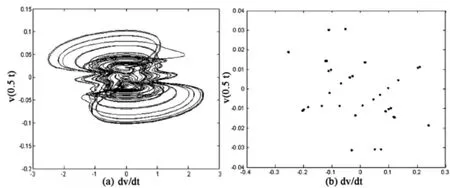
图 7 混沌运动:c0=15．25，c1=3．5，⒜相图⒝庞加莱截面Fig．7 chaotic motion appears when c0=15．25，c1=3．5，⒜ phase portraits ⒝ Poincare map

图8 10 倍周期运动:c0=15．25，c1=2．3，⒜相图⒝庞加莱截面Fig．8 periodic － 10 motion appears when c0=15．25，c1=2．3，⒜ phase portraits ⒝ Poincare map

4 结论

本文用微分求积法求解了轴向加速粘弹性梁横向振动的控制方程，并在数值结果的基础上利用分叉图分析了轴向定常加速度、轴向加速度变化幅值对轴向加速粘弹性梁面内横向振动的非线性动力学行为的影响．为了验证通过分叉图得到的一些非线性动力学性质比如周期、混沌，作出了相应的相图，庞加莱截面．以上结果表明用微分求积法分析这一类工程结构的非线性动力学性质是非常有效的．

1 Ravindra B，Zhu W D．Low dimensional chaotic response of axially accelerating continuum in the supercritical regime．Archive of Applied Mechanics，1998，68:195 ～205

2 Marynowski K，Kapitaniak T．Kelvin－Voigt versus Burgers internal damping in modeling of axially moving viscoelastic web．International Journal of Non－linear Mechanics，2002，37:1147～1161

3 Yang X D，Chen L Q．Bifurcation and chaos of an axially accelerating viscoelastic beam．Chaos，Solitons and Fractals，2005，23(1):249～258

4 Chen L H，Zhang W，Yang F H．Nonlinear dynamics of higher－dimensional system for an axially accelerating viscoelastic beam with in－plane and out－of－plane vibrations．Journal of Sound and Vibration，2010，329:5321 ～5345

5 Ding H，Chen L Q．On two transverse nonlinear models of axially moving beams．Science in China Series E:Technological Sciences，2009，52(3):743 ～751

6 Bellman R，Kashef B G，Casti J．Differential quadrature:a technique for the rapid solution of nonlinear partial differential equations．Journal of Computational Physics，1972，10:40～52

7 Shu C．Differential quadrature and its application in engineering．Springer:Berlin，2000

*The project supported by the National Natural Science Foundation of China(11290152，10732020，11072008)

† Corresponding author E－mail:sandyzhang0@yahoo．com

ANALYSIS ON NONLINEAR DYNAMICS OF AN AXIALLY ACCELERATING VISCOELASTIC BEAM USING DQM*

Wang Dongmei1，2Zhang Wei1†Liu Yan1，3
(1．College of Mechanical Engineering Beijing University of Technology，Beijing100022，China)(2．Department of Mathematics Jining University，Qufu272155，China)(3．Department of Physics and Electronic Information China West Normal University，Nanchong，Sichuan637002，China)

The differential quadrature method(DQM)was developed to solve numerically the nonlinear partialdifferential equation of the nonlinear transverse vibration of an axially accelerating viscoelastic beam．Based on the numerical solutions，the nonlinear dynamical behaviors，such as bifurcations and chaotic motions of the nonlinear system，were investigated by use of Poincare map，phase portrait．

DQM， nonlinear partial－differential equation， numerical solution， chaos， bifurcations

22 April 2012，

18 June 2012．

10．6052/1672－6553－2013－007

2012－04－22 收到第 1 稿，2012－06－18 收到修改稿．

*国家自然科学基金重大项目资助(11290152)和国家自然科学基金(10732020，11072008)资助项目

E－mail:sandyzhang0@yahoo．com