基于NARMAX模型和NOFRF结构损伤检测的实验研究*
程长明 彭志科 孟光
(上海交通大学,机械系统与振动国家重点实验室,上海 200240)
基于NARMAX模型和NOFRF结构损伤检测的实验研究*
程长明 彭志科†孟光
(上海交通大学,机械系统与振动国家重点实验室,上海 200240)
非线性输出频率响应函数是由Volterra级数发展而来的频域概念,可方便在频域对非线性系统进行分析,它是频率的一维函数.本文主要介绍了利用NARMAX模型以及NOFRF对结构进行损伤检测的方法,并利用实验研究证实了该损伤检测方法的可行性.另外,由于系统非线性特性可用来做结构损伤检测,且具有对系统状态比较敏感的优点,而基于NOFRF的损伤检测方法是利用非线性方法来分析系统的状态,该方法提取出的特征属于非线性特征,所以该损伤检测方法可以用来做结构损伤检测,且具有对系统状态比较敏感的优点.
Volterra级数, NARMAX模型, 非线性输出频率响应函数, 广义频率响应函数, 损伤检测
引言
众所周知,若不能及时发现结构中的损伤可能会引发重大事故,所以准确及时地识别出工程结构当中的损伤,对于防止恶性事故的发生、减少生命财产损失具有重要的意义.研究人员对此做了大量研究,取得了一定的进展,提出了多种损伤检测技术.其中,由于振动测试法具有信号易提取、测点无需苛刻要求和结构动态响应的全局性等优点,受到许多研究人员的重视.一般认为结构损伤会引起结构物理参数的变化,从而使结构模态参数发生变化,如频率变化[1]、振型变化、曲率模态变化[2-3]以及模态柔度(刚度)变化[4]等等.于是基于上述不同的参数,人们提出了多种基于模态测试数据的损伤识别方法.
但是,一些学者[5-7]研究发现结构的线性特征对结构的变化不够敏感.例如,文献[5]数值研究结果显示具有占截面面积10~20%裂纹的梁,固有频率仅仅降低了0.6 ~1.9%.Chen[7]研究结果表明,当槽钢达到损坏的临界点时,实验测得该槽钢的前四阶模态频率仅仅分别下降4.9%,2%,2.9%,3.6%,而用有限元模型分析时该槽钢前四阶模态频率变化的更小.另外,Ellis和 Jeary[8]研究结果表明,变化的环境下,测量得到的模态频率存在高达3%的变化,Askegaard和Mossing[9]等的研究结果证实了这一点,并且显示一座桥梁在没有任何明显变化的情况下,一年以后固有频率居然变化了10%.Chen[7]研究结果表明仅利用系统的模态频率以及模态振型不足以对结构进行损伤检测以及损伤定位,需要研究出较结构模态频率以及模态振型对结构状态更加敏感的特征来对结构进行损伤检测.
一般而言,结构系统发生损伤后,结构会产生非线性特征.基于此考虑,许多学者研究利用非线性振动方法对结构进行损伤检测[6,10,11].Tsyfanskii[12]和他的同事研究一根棒的振动响应时,发现棒的非线性特征对裂纹(即使是非常小的裂纹)的存在非常敏感.Bovsunovsky和 Surce[5]证实了这一点,并且研究表明系统非线性特征比固有频率或模态振型对裂纹的存在更加敏感.基于亚谐共振,Tsyfanskyh 和 Beresnevich[6]提出了一种用于检测非线性弹性梁中疲劳裂纹的新方法.
基于以上考虑,本文提出了一种新的基于系统非线性特征的结构损伤检测方法,该结构损伤检测方法是一种基于NARMAX模型和NOFRF的结构损伤检测方法.
1 NARMAX模型及非线性输出频率响应函数
1.1NARMAX 模型
NARMAX模型表示系统输入与输出之间的非线性函数关系,该函数是一个非线性差分方程,如下式所示

其中,ny,nu,ne分别是时刻k时,系统输出、输入与噪声项的最大延迟数,u(k),y(k)分别是系统的输入与输出,[·]是一个非线性函数.实际工程当中,噪声项e(k)是无法直接通过测量得到,而是用预测误差代替,即,

其中,^y(k)是预测的输出,y(k)为测量得到的实际输出.
假设函数[·]是阶数为Nl的多项式函数.为了估计该函数的参数,方程(1)可以用下式表示

其中,pi(k)代表NARMAX模型当中的项,pi(k)≠pj(k)(i≠j),N为数据的长度,nθ是预选项的个数,θi是待估计的模型参数.
本文利用正交前向回归最小二乘算法对系统的NARMAX模型进行辨识.正交前向回归最小二乘算法的基本思想是将较高维(例如M维)的参数估计问题,转化成较低维(例如Ms维,且Ms<M)的参数估计问题,也即从原来M个预选项的非线性模型当中提取出最重要的Ms项的过程.该算法可以独立地从系统的非相关项中估计出系统的参数,并可计算出模型每一项对系统能量的贡献.该算法有效地将参数估计与结构辨识集合成为一个简单的过程,从而简化了非线性系统辨识这一复杂的问题.
现将正交前向回归最小二乘算法的具体步骤归纳如下:
(1)确定模型预选项的总个数,例如M,令所有的预选项pi(k),i=1,2,…,M等于w1(k).
(2)i=1,2,…,M计算
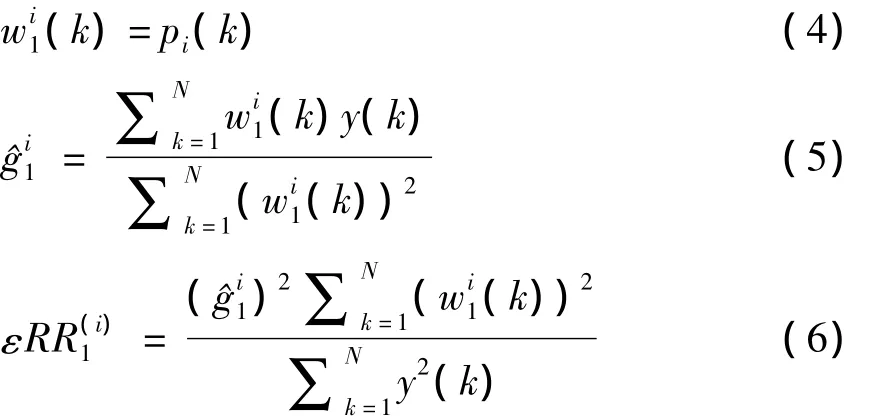
(3)找出的最大值,例如=max{,1≤i≤M},那么在这个模型当中第一个被选择的就是方程(3)中的第j项,例如w1(k)=pj(k).
(4)考虑所有的pi(k),i=1,2,…,M,i≠j作为w2(k)的预选项.令i=1,2,…,M,i≠j,计算


结束选项,至此,选出了一个只有Ms个重要项的模型.
为了检验辨识得到的NARMAX模型是否与实际系统相符合,还需要对其进行相关的验证.Billings[13]研究结果显示对于辨识得到的NARMAX模型,如果满足以下条件,那么辨识得到的NARMAX模型是有效的.

(5)找出的最大值,例如=max{,1≤i≤M,i≠j},那么在这个模型当中第二个被选择的就是方程(3)的第l项,例如

(6)根据上面的选项方法,继续选项,直到误差减小率达到设定的允许误差,则结束选项.假设允许误差为ρ,若
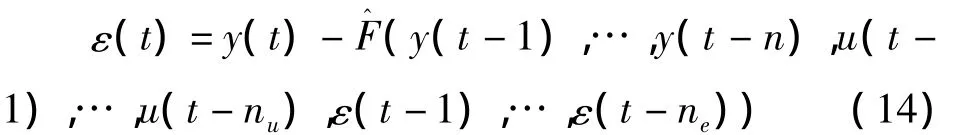
其中,ε(t)是残差,即(·)代表辨识得到的NARMAX模型.
由于实际工程当中,只能根据有限长度的数据来辨识结构模型,所以基于方程(13)的模型有效性检验可引入一个置信区间,如果方程(13)中相关函数的值在置信区间内,就可认为它们之间没有发现明显的相关性,即辨识出的模型是有效的.
1.2 非线性输出频率响应函数
对于可以用Volterra级数[14]表示的非线性系统,它的输出频谱可以用下式表示,
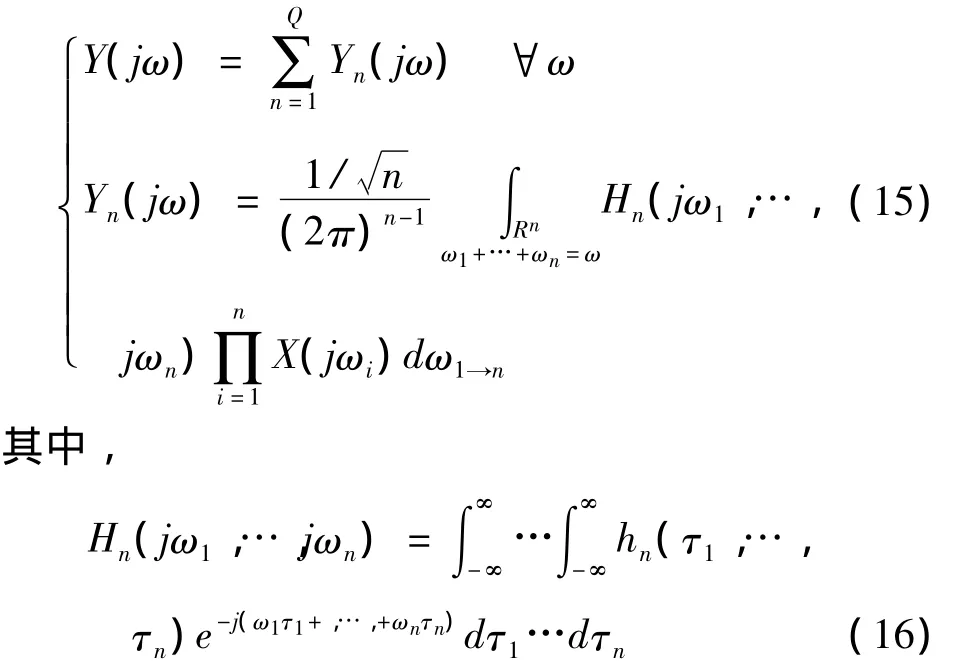
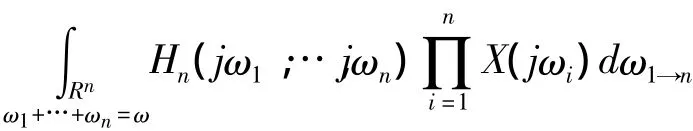
根据方程(15),Lang 和 Billings[15,16]提出了一个新的频域概念-非线性输出频率响应函数,定义如下
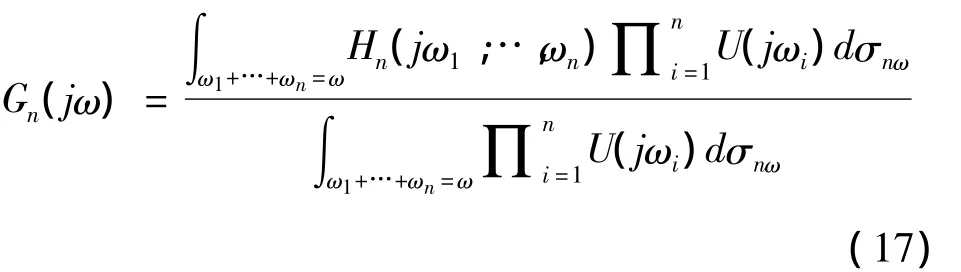
图1 线性系统的输入输出频域表示Fig.1 The relationship between output and input frequency spectrum in linear system

引入非线性输出频率响应函数Gn(jω),n=1,…,N后,系统的输出频谱可以改用下式表示,方程(18)表示的非线性系统输出频谱与线性系统输出频谱比较相似,因为对于线性系统,系统的输出频谱与输入频谱之间的关系可用图1表示;对于非线性系统,可用图2表示.
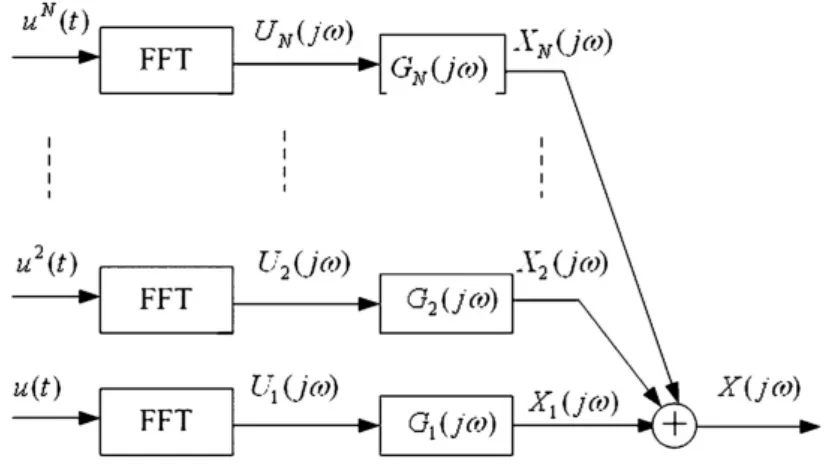
图2 非线性系统输入输出频域表示Fig.2 The relationship between output and input frequency spectrum in nonlinear system
从非线性输出频率响应函数的定义式可以看出非线性输出频率响应函数不仅与非线性系统本身的特性有关,而且与系统输入也有关,它反映的是非线性系统在特定类型的输入下表现出来的频率响应特性,它最大的优点是各阶次的函数都是一维的,从而可方便地用图表来表示和分析解释,也较容易根据系统的输入、输出信号估计得到.因此,可以基于非线性输出频率响应函数,用与分析线性系统类似的方法来分析非线性系统.
2 基于NOFRF的损伤检测方法
NARMAX模型分析方法是根据结构系统的检测信号和相应的响应信号辨识得到系统的NARMAX模型,然后根据辨识得到的NARMAX模型,去掉NARMAX模型当中所有与噪声项e(t)有关的项,从而得到系统的NARX模型.NARX模型可以用来表示复杂结构系统的动力特性,所以任何损伤引起的系统物理特性的改变都会反应在辨识得到的NARX模型当中.但是,表示结构系统的NARX模型一般不是唯一的,而且大多数情况下,具有很多项,这表示一般很难从已辨识出的NARX模型当中直接提取出被检测结构的物理特征.幸运的是,不管结构系统已辨识出的NARX模型具有多少不同的形式,只要正确获得了系统的动力特性,系统的频域表示就是唯一的,例如广义频率响应函数就是唯一的[17,18].因此,已辨识出的 NARX 模型的广义频率响应函数可以更好地说明被检测结构系统的状态.
虽然理论上非线性系统的广义频率响应函数可以根据它的NARX模型计算出来,然而由于广义频率响应函数的多维性,使得它在实际应用中遇到了很大的难题.与广义频响函数不同的是,非线性输出频响函数与非线性系统本身的特性和系统输入都有关,它反映的是非线性系统在特定类型的输入下表现出来的频率响应特性,它最大的优点是各阶次的函数都是一维的,从而可方便地用图表来表达和进行分析解释,也较容易根据系统输入输出信号辨识估计得到.
从非线性输出频率响应函数的定义式可以看出,非线性输出频率响应函数Gn(jω)是广义频率响应函数Hn(jω1,…,jωn)在n维超平面 ω1+ …ωn=ω的加权平均,其中加权值与系统的输入信号有关.因此,非线性输出频率响应函数Gn(jω),n=1,…,N是另外一种表示结构系统动力特性的频域概念,系统广义频率响应函数在正常与损伤状态下的不同在非线性输出频率响应函数当中也能体现.总之,非线性输出频率响应函数可以用来描述被检测结构系统的特征,从而可以根据它们的值来判断系统是否有损伤.
根据方程(18),并且假设用系统的前四阶非线性输出频率响应函数足够表示系统的输出频率响应.那么,系统输出的频率成分可以写成下式,

从方程(19)可以看出,用两个频率相同幅值不同的谐波信号激励系统,就可以求出方程(19)当中的各阶非线性输出频率响应函数,因此,分别采用幅值为A(1)和A(2)的两个正弦信号激励系统,得到两组系统时域响应y(1)(t)和y(2)(t),它们的频谱为Y(1)(jω)和Y(2)(jω),记两次激励为(·)和(·),(k=1,2,3,4),根据方程(19),可得
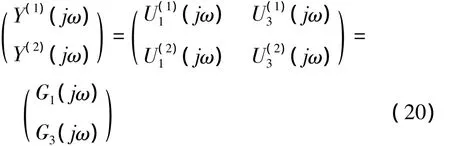
G1(jω)和G3(jω)可以根据下式计算

同理,可以计算出G2(j2ω)和G4(j2ω)等.
为了方便分析,定义一个基于非线性输出频率响应函数的指标,该指标定义如下,
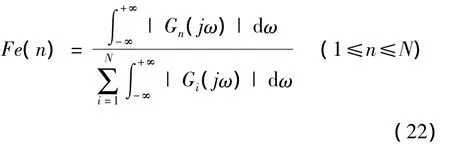
用该指标表示被检测结构系统的特征.由于Fe(n)=1,该指标反映了系统各阶非线性的强度.例如,Fe(1)≈1表示系统基本上是线性的;Fe(5)≈1表示第5阶系统非线性占系统的主要地位.因此,N个Fe(n),n=1,…,N的值组合起来可以描述被检测结构系统的非线性状态,同时可以用于结构损伤的检测.

图3 操作流程图Fig.3 Operation flow chart
根据上面介绍的基于NARMAX模型以及非线性输出频率响应函数对结构系统进行损伤检测的操作步骤,下面对其做一个总结,
第一步:给待检测的结构系统一个宽频的激励信号.
第二步:根据检测信号及相应的响应信号辨识得到系统的NARMAX模型,根据获得的NARMAX模型,得到系统的NARX模型.
第三步:对获得的NARX模型进行仿真研究,即使用N~个频率相同幅值不同的谐波信号作为NARX模型的输入,计算NARX模型的响应.
第四步:根据文献[16,19]中的算法以及第三步中获得的系统输入、输出数据估算系统的非线性输出频率响应函数Gn(jω),n=1,…,N.
第五步:根据方程(22)计算出特征的值Fe(n),n=1,…,N.
操作流程图如图3所示.
3 实验研究
对图4所示的桥梁模型结构进行损伤检测,以验证本文所述损伤检测方法的可行性.该桥梁模型结构中的损伤是通过将连接桥梁结构的螺栓旋松来模拟日常桥梁结构的松动所导致的损伤.实验流程图如图5所示.利用白噪声源产生一个宽频的白噪声信号,并利用低通滤波器对其进行滤波,使其能量更加集中;由于白噪声源产生的信号能量有限,所以需要线性功率放大器对其进行功率放大,并利用经线性功率放大器放大后的白噪声信号驱动激振器激励桥梁模型结构;同时利用力传感器测量激振器激励桥梁模型结构激励力的大小;另外,由于力传感器产生的电荷信号比较微弱,所以需要先经电荷放大器对该信号进行放大并转换成电压信号,再由信号采集仪对其进行采集;并利用加速度传感器测量桥梁结构在白噪声激励下的响应信号,并用信号采集仪对其进行采集.

图4 桥梁模型实验图形Fig.4 Experiment picture of bridge model
该试验中所用的设备名称以及型号如表1所示,其中,白噪声源产生频率范围为0~20kHz的高斯白噪声,滤波器采用0~500Hz的低通滤波,采样频率为5208Hz.

表1 实验仪器名称以及型号Table 1 The name and style of experiment equipment
另外,值得注意的是,两种情况下除了连接螺栓是否被旋松以外,其它的实验条件都是一样的,因此最终分析结果的不同可以完全反应出桥梁模型结构在这两种状态下结构特性的不同,所以分析的结果可以用于检测桥梁模型结构是否存在损伤.
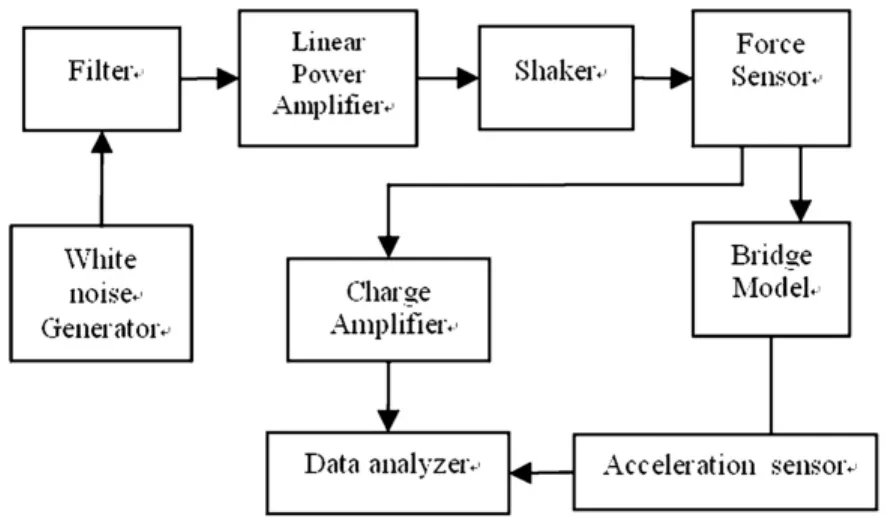
图5 实验流程图Fig.5 Experiment flow chart
下面是根据本文所述损伤检测方法具体的实施过程.
1,对桥梁结构系统施加频率范围为0~500Hz的激励信号.
2,根据实验数据辨识得到桥梁结构的NARMAX模型.
(1)基于正交前向回归最小二乘算法辨识出结构不同状态(正常与损伤)下的NARMAX模型
本实验采用第500到第2000的采样数据来辨识桥梁模型结构的NARMAX模型,然后根据辨识得到的 NARMAX模型,得到桥梁模型结构的NARX.正常状态下所测桥梁模型结构的NARX表达式如方程(23)所示,连接螺栓旋松状态下所测桥梁模型结构的NARX表达式如方程(24)所示.


(2)模型有效性验证

图6 正常状态下相关性验证图形Fig.6 Correlation validation figure under undamaged statement
3,对辨识得到的NARX模型进行仿真研究,即在两个频率相同幅值不同的谐波信号激励下,分别计算系统NARX模型的响应.
在此实验当中,两次采用的激励谐波信号为正弦信号,频率为40Hz,采样频率400Hz,两次的幅值A(1)和A(2)分别为1.1 和1.7.
4,根据不同幅值激励下NARX模型的响应求出桥梁模型结构的非线性输出频率响应函数.
根据NARX模型在两个不同输入下的响应,并利用方程(21)可以估算桥梁模型频率为40Hz时非线性输出频率响应函数的值.计算结果如表2所示.
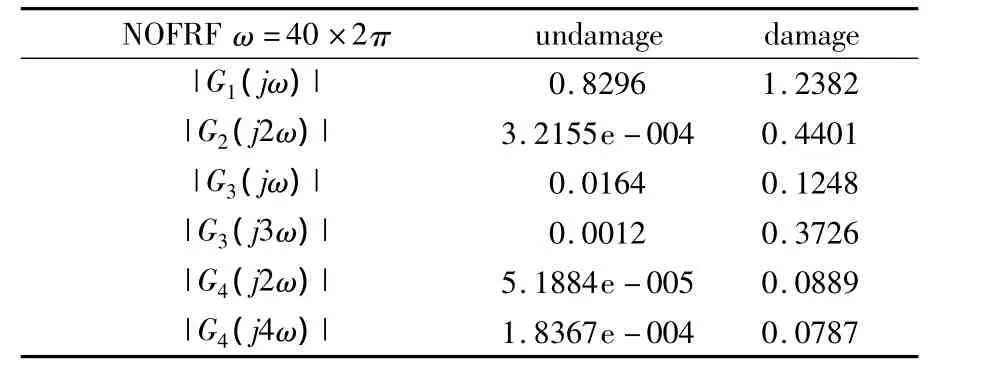
表2 桥梁模型不同状态下非线性输出频率响应函数值Table 2 The value of NOFRF under different condition from bridge model
5,求出非线性输出频率响应函数相关指标的值根据非线性输出频率响应函数相关指标的定义(方程(22)),计算得到两种状态下桥梁模型结构非线性输出频率响应函数相关指标在频率为40Hz时的值,如表3所示.
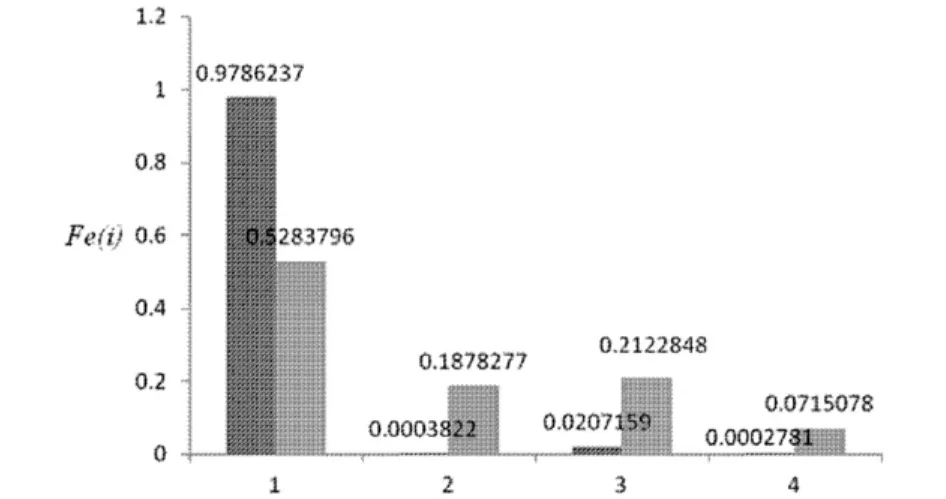
图7 桥梁模型不同状态下非线性输出频率响应函数相关指标的值:左侧-正常状态;右侧-损伤Fig.7 The value of the index based on NOFRF under different condition from bridge model:left-undamaged;right:damaged
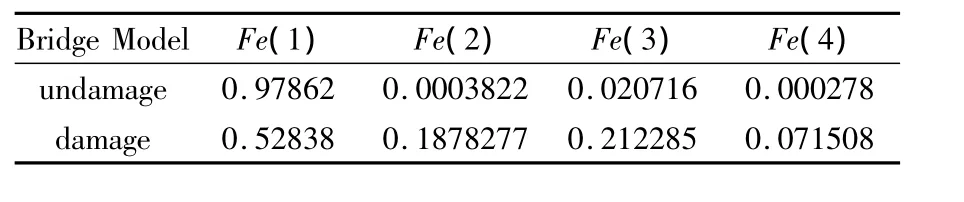
表3 桥梁模型不同状态下的非线性输出频率响应函数相关指标的值Table 3 The value of index based on NOFRF under different condition from bridge model
为了更好地表示两种状态下的分析结果,图7给出了桥梁模型结构两种状态(正常与螺栓旋松)下,非线性输出频率响应函数相关指标的值.
表3或图7中的实验结果证实,通过比较两种不同状态下系统非线性输出频率响应函数相关指标的值来判断系统是否存在损伤是切实可行的.
4 结论
本文提出了一种综合运用NARMAX模型和NOFRF分析方法对结构系统进行损伤检测的方法.该新的损伤检测方法主要包括三个部分:首先,利用仿真或实验输入、输出数据辨识得到结构系统的NARMAX模型,根据得到的NARMAX模型得到结构系统的NARX模型;然后,根据获得的NARX模型,计算系统在谐波激励下的非线性输出频率响应函数以及与之相关指标的值;最后,通过比较不同状态下系统的非线性输出频率响应函数相关指标的值来判断系统是否存在损伤.
1 万小朋,王军强,赵美英.基于模态频率和神经网络的结构损伤检测.西北工业大学学报,2003,21(2):156~159(Wan X P,W ang J Q,Zhao M Y.Structural damage monitoring based on vibration modal analysis and neural network technique.Journal of Northwestern Polytechnical University,2003,21(2):156~159(in Chiniese))
2 叶黔元,翟立祥,陈锦辉.曲率模态及其在桁架桥梁损伤识别中应用.力学季刊,2005,26(2):286~292(Ye Q Y,Zhai L X,Chen J H.Application of curvature mode shape in damage identification of truss bridge.Chinese Quarterly of Mechanics,2005,26(2):286 ~292(in Chiniese))
3 王山山,任青文.基于曲率模态振型的刚架结构损伤检测.动力学与控制学报,2005,3(2):81 ~86(Wang S S,Ren Q W.Damage detection for frame structure using curvature mode shapes.Journal of Dynamics and Control,2005,3(2):81 ~86(in Chinese))
4 曹晖,Michael I F.基于模态柔度曲率的损伤检测方法.工程力学,2006,23(04):33~38(Cao H,Michael I.F.Nondestructive damage evaluation indicator based on modal flexibility curvature.Engineering Mechanics,2006,23(04):33~38(in Chiniese))
5 Bovsunovsky A P,Surace C.Considerations regarding superharmonic vibrations of a cracked beam and the variation in damping caused by the presence of the crack.Journal of Sound and Vibration,2005,288(4-5):865 ~886
6 Tsyfansky S L,Beresnevich V I.Detection of fatigue cracks in flexible geometrically non-linear bars by vibration monitoring.Journal of Sound and Vibration,1998,213(1):159~168
7 Chen H L,Spyrakos C C,Venkatesh G.Evaluating structural deterioration by dynamic response.Journal of Structural Engineering-American Society of Civil Engineers,1995,121(8):1197~1204
8 Ellis B R,Jeary A P.Recent work on the dynamic behavior of tall buildings at various amplitudes,1980:313 ~316
9 Askegaard V,Mossing P.Long term observation of RC-bridge using changes in natural frequency.Nordic concrete research,1988(7):20~27
10 Lang Z Q,Peng Z K.A novel approach for nonlinearity detection in vibrating systems.Journal of Sound and Vibration,2008,314(3-5):603 ~615
11 Somnay R J,Ibrahim R A,Banasik R C.Nonlinear dynamics of a sliding beam on two supports and its efficacy as a non-traditional isolator.Journal of Vibration and Control,2006,12(7):685~712
12 Tsyfanskii S L,Magone M A,Ozhiganov V M.Using nonlinear effects to detect cracks in the rod elements of structures.The Soviet Journal of Nondestructive Testing,1985,21:224 ~229
13 Swain A K,Billings S A,Stansby P K.et al.Accurate prediction of non-linear wave forces:Part I(Fixed cylinder).Mechanical Systems and Signal Processing,1998,12(Compendex):449~485
14 Lang Z Q,Billings S A.Output frequencies of nonlinear systems.International Journal of Control,1997,67(5):713~730
15 Lang Z Q,Billings S A,Tomlinson G R.et al.Analytical description of the effects of system nonlinearities on output frequency responses:A case study.Journal of Sound and Vibration,2006,295(3-5):584 ~601
16 Lang Z Q,Billings S A.Energy transfer properties of nonlinear systems in the frequency domain.International Journal of Control,2005,78(5):345 ~362
17 Billings S A,Tsang K M.Spectral analysis for non-linear systems,Part I:Parametric non-linear spectral analysis.Mechanical Systems and Signal Processing,1989,3(4):319~339
18 Billings S A,Tsang K M.Spectral analysis for non-linear systems,Part II:Interpretation of non-linear frequency response functions.Mechanical Systems and Signal Processing,1989,3(4):341~359
19 Peng Z K,Lang Z Q,Billings S A.Crack detection using nonlinear output frequency response functions.Journal of Sound and Vibration,2007,301(3-5):777~788
*The project supported by the National Science Fund for Distinguished Young Scholars(11125209)and the National Natural ScienceFoundation of China(10902068,51121063)
† Corresponding author E-mail:z.peng@sjtu.edu.cn
THE EXPERIMENTAL STUDY OF DAMAGE DETECTION BASED ON NARMAX MODEL AND NOFRF*
Cheng Changming Peng Zhike†Meng Guang
(State Key Laboratory of Mechanical System and Vibration,Shanghai Jiao Tong University,Shanghai200240,China)
The nonlinear output frequency response functions(NOFRF)which is derived from the Volterra series can facilitate the analysis of nonlinear systems in frequency domain,it is a one dimensional function of frequency.The paper introduces the structural damage detection method which is based on NARMAX model and NOFRF.An experimental study demonstrates the feasibility of the structural damage detection method.Because the nonlinear characteristics of system can be used for the detection of structural damage,and is sensitive about the state of system,in addition,the structural damage detection method which is based on NARMAX model and NOFRF is a nonlinear method for analyzing the state of system,the characteristics extracting from system is a nonlinear characteristics,so the damage detection method can be used for the detection of structural damage,and has the advantage which is sensitive to the state of system.
Volterra series, NARMAX model, nonlinear output frequency response functions, damage detection
21 April 2012,
11 June 2012.
10.6052/1672-6553-2013-015
2012-04-21 收到第 1 稿,2012-06-11 收到修改稿.
*国家杰出青年科学基金资助项目(11125209)和国家自然科学基金资助项目(10902068,51121063)
E-mail:z.peng@sjtu.edu.cn

