外电场作用下改进的 Leaky Integrate-And-Fire模型的峰放电频率适应性研究*
韩春晓 王江 常莉 车艳秋
(1.天津职业技术师范大学自动化与电气工程学院,天津 300222)(2.天津大学电气与自动化工程学院,天津 300072)
外电场作用下改进的 Leaky Integrate-And-Fire模型的峰放电频率适应性研究*
韩春晓1王江2†常莉2车艳秋1
(1.天津职业技术师范大学自动化与电气工程学院,天津 300222)(2.天津大学电气与自动化工程学院,天津 300072)
峰放电频率适应性是神经元在信息处理过程中重要的动力学特性之一.当神经系统受到外电场作用时,会对其动力学行为以及神经电信息的产生、传导产生影响.我们基于Leaky integrate-and-fire(LIF)神经元模型,建立了外电场作用下改进的LIF神经元模型.采用随时间演化的膜电位曲线和峰放电频率曲线,以及随外电场变化的起始峰放电频率曲线和稳态峰放电频率曲线,研究不同强度、频率外电场作用下改进的LIF模型的适应性变化.此外,还利用相邻峰峰间期(ISI)之间的相关性进一步阐明外电场对神经元适应性的影响.
峰放电频率适应性, 外电场, Leaky integrate-and-fire模型, ISI, 相关性
引言
峰放电频率适应性 (spike-frequency adaptation,SFA)是指神经元在持续外界刺激下瞬时峰放电频率逐渐降低的现象,是神经元普遍存在的特性之一,在神经信息处理中起到重要作用.目前已在很多物种的神经元中发现了峰放电频率适应性,如小龙虾的牵引感受器等[1],啮齿类动物运动神经元[2],海马 CA1 椎体细胞[3],梨状皮质椎体细胞[4],猫的视觉皮层神经元[5],脊髓运动神经元[6],以及人类大脑皮层[7-11]等.人们对峰放电频率适应性的功能意义有如下几种猜测,如弱信号的前向掩蔽[12],选择性注意[13],逼近刺激的选择性响应[14]等.
从生物物理角度看,神经元峰放电频率适应性是由 M-type 电流[15]、AHP-type 电流[16]和/或钠激活钾电流[17]等多种离子电流作用所致.Integrateand-fire(IF)模型是描述神经元峰放电行为的最简单的模型[18-20],使得该类神经元模型具备适应性的一种方法就是由刺激处引入反馈变量,即适应性变量[21-22].2010 年 Benda 等人发现了 Leaky integrateand-fire(LIF)模型在受到直流刺激时具有典型的适应性[23-24].目前已有研究成功利用具有适应性变量的LIF模型复现皮质锥体细胞的峰放电行为[25-26].
外电场对于生物致病以及治病都产生很大影响.一方面,由于高压电线及用电设备的广泛应用,目前环境中电磁辐射强度较上世纪增强近一百万倍[27].外电场能够改变神经元的动态行为,并影响神经信息的产生及传导,如外电场与细胞内信息传导通路相互作用,可以改变神经元钙振荡周期,从而影响神经元峰放电频率,并引起神经系统功能失常[28-29].另一方面,电磁刺激作为一种物理治疗手段越来越受到人们的关注,如经颅磁刺激(Transcranial Magnetic Stimulation,TMS)和深部脑刺激(Deep brain stimulation,DBS)等.TMS是一种无创式的治疗方法,它基于电磁感应原理,通过快速变化的磁场产生弱电场,引起大脑特定点或者区域产生响应[30].DBS则是一种有创的治疗方式,它通过脑外科手术将导线植入脑部的特定位置,利用“脑起搏器”发出电脉冲刺激,来调节脑部的不正常活动,目前对慢性疼痛、帕金森病、震颤和肌张力障碍等难治性运动和情感性精神障碍等疾病取得显著的疗效[31-32].因此,研究外电场对神经系统的影响是十分有意义的.
在研究外电场对神经系统的影响时,其强度和频率是两个重要参数.如Gluckman等人研究了不同强度的弱外电场对海马CA1和CA3区神经元同
2012-08-16 收到第 1 稿,2012-09-13 收到修改稿.
*国家自然科学基金资助项目(61104032,61072012,61172009,50907044)和学校科研启动经费项目(KYQD11005)
综上所述,我们有必要研究外电场与神经系统适应性之间映射关系,于是本文利用LIF模型研究外电场对神经元峰放电频率适应性的影响.首先,基于Benda提出的LIF模型描述恒定电流作用下神经元的适应性;然后引入适应性变量,建立外电场作用下改进的LIF模型,从膜电位曲线、峰放电频率曲线、起始峰放电频率曲线、稳态峰放电频率曲线,相邻峰峰间期(ISI)相关性等多角度阐明,在外电场作用下改进的LIF神经元模型具有峰放电频率适应性,并给出仿真结果.
1 模型和方法
1.1 LIF 模型
LIF模型可以描述神经元膜电位的动力学行为,其膜电位随输入刺激电流的动态响应过程可由下式来表示[23]:

式中,τV是时间常数,R是输入阻抗.在刺激电流I(t)作用下,当膜电位V超过阈值Vth时,神经元会产生一个峰放电,同时V复位至静息电位Vr.定义适应性电流IA,形式如下:

式中是最大电导,α是门变量,EA是反电势,稳态变量 α∞(V)是关于膜电位V的 Sigmoid函数[22].于是膜电位可以表示成如下形式:
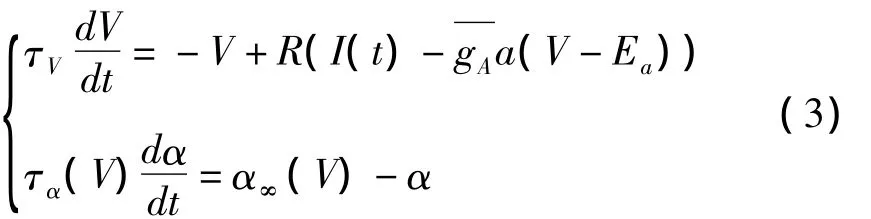
我们用常数c近似(V-EA),并引入适应性变量A=,带入式(3),于是具有适应性变量的LIF模型如下式所示:
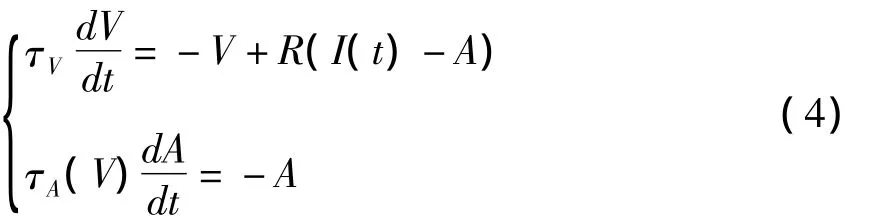
当V超过阈值Vth时,V将复位至Vr,且适应性变量A增加ΔA=.各参数取值如下:τV=10ms,Vth=10mV,Vr=0mV,R=1MΩ,τA=100ms,ΔA=2nA.本文采用前向欧拉法对LIF模型进行数值仿真模拟,仿真步长为Δt=0.005ms.
定义峰峰时间间隔(Interspike Interval,ISI)为相邻两个峰放电之间的时间间隔,峰放电频率为相应ISI的倒数.其中起始峰放电频率f0为神经元受到刺激作用后所产生的首个ISI的倒数,稳态峰放电频率f∞为神经元峰放电频率达到稳定状态的值.
图1给出了LIF模型在恒定电流作用下的动态响应.当膜电位超过阈值10mV时,神经元产生一个峰放电,同时R(I-A)随着适应性变量A的增加而降低,使得神经元膜电位到达阈值的时间变慢,于是,峰放电频率由起始峰放电频率f0逐渐降低,趋近于稳态值f∞.

图1 恒定电流作用下LIF模型的动态响应(a)膜电位曲线;(b)峰放电频率曲线Fig.1 Dynamic responses of LIF model under the direct current.(a)membrane potential curve;(b)spike-frequency curve.
1.2 LIF模型适应性
若神经元不具备适应性,则神经元输入输出之间的映射关系完全可以由f-I曲线表征;然而由于适应性的存在,仅通过f-I曲线无法全面刻画神经元的输入输出关系,我们还需要考察在不同适应性变量A的情况下,神经元起始放电频率f0随刺激I的变化规律,即起始峰放电频率曲线f0(I,A0).此外,稳态峰放电频率曲线f∞(I)用于描述LIF模型在给定输入情况下的适应性稳态响应.由于f0(I,A0)曲线和f∞(I)曲线可以充分描述神经元的适应性行为[13][35][36][37],因此本文没有考虑神经元除起始状态及稳态之外的其他中间状态的f-I曲线.
如图2所示,(a)为给定恒定输入电流I=26nA,当A0=0nA时,f0=205Hz;当A0=5nA时,f0=155Hz.(b)为f0(I,A0)曲线和f∞(I)曲线.随着适应性参数初始值A0不断的增加,f0(I,A0)曲线会沿着刺激强度增大的方向水平向右偏移,这是由于A0增加会导致膜电位到达阈值的时间增加,那么起始峰放电频率f0就会降低.然而A0对于稳态峰放电频率f0没有太大影响,在不同A0的情况下,对于任意给定的恒定输入I其f∞都趋于一致,而随着输入强度的不断增加,f∞也随之增加,并趋于线性.

图2 LIF模型恒定电流刺激下峰放电频率曲线.(a)当I=26nA时的f(t,A0)曲线;(b)起始峰放电频率曲线f0(I,A0)和稳态峰放电频率曲线f∞(I).Fig.2 Spike - frequency curves of LIF model under the direct current.(a)f(t,A0)curve when I=26nA;(b)onset spike - frequency curve f0(I,A0)and steady state spike - frequency curve f∞ (I).
依据ISI定义,由多个峰放电组成的膜电位时间序列可以转换成 ISI序列{Δt1,Δt2,…,ΔtN}.则相应ISI序列平均值为
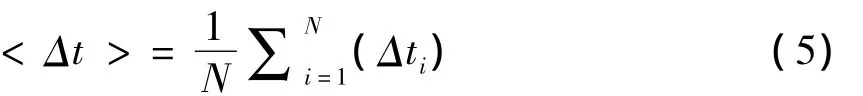
ISI序列的方差为

ISI序列中任意相邻ISI之间的协方差为
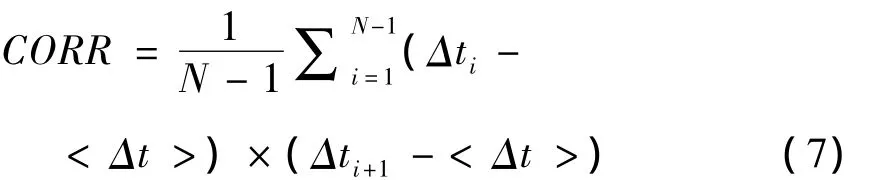
则ISI序列中任意相邻ISI之间的相关系数为

式中CC∈[-1,1].对于泊松过程,甚至任意更新过程,任意相邻ISI之间不存在相关性,因此CC=0.而对于LIF模型,当对其输入强度足够大时,随着强度的不断增强,相邻ISI相关性随之降低,并且A0的改变对相邻ISI相关性影响很小,如图3所示.
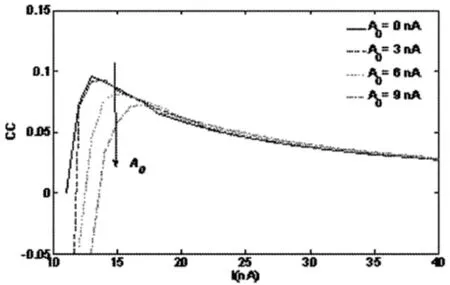
图3 LIF模型在恒定电流作用下相邻ISI相关性Fig.3 Correlation between successive ISI of LIF model under the direct current
1.3 外电场作用下改进的LIF模型
为研究外电场对神经元适应性的影响,本文在LIF模型上基础上引入外电场参数VE,于是有外电场作用下改进的LIF模型,如下所示:
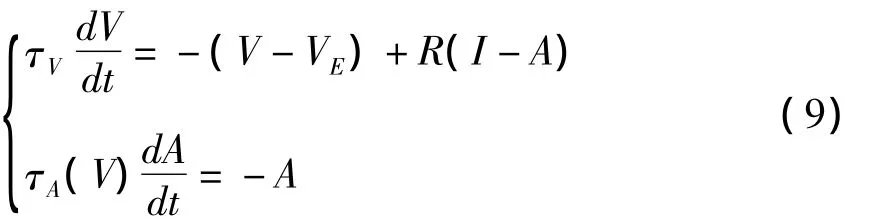
对于神经元动力学行为研究,无论是电生理实验还是数值仿真,人们普遍采用恒定刺激或者脉冲刺激作为神经元外部刺激[38].然而,对于实际的神经系统,诱发神经元放电的并非脉冲形式的电流或电场,相比而言,正弦信号更贴近实际情况[34][35][39].因此我们定义外电场形式为交流外电场VE=Vssin(2πfint),其中Vs为交流外电场强度,fin为交流外电场频率;由于我们主要讨论外电场对LIF模型适应性的影响,所以令I=0,其余参数设定与式(4)相同.
2 仿真结果
2.1 不同强度交流外电场对改进的LIF模型的影响
为研究不同交流外电场强度对改进LIF模型的影响,首先,令交流外电场频率为定值fin=40Hz.仿真结果如图4所示,当交流外电场强度Vs=20mV时,起始峰放电频率f0=90Hz;当Vs=30mV时,f0=150Hz,且随着时间的演化,峰放电频率f逐渐减小并趋于稳态.然而Vs不同,f达到稳态所需要的时间也有所不同,如Vs=20mV和30mV相比,当Vs=20mV时达到稳态所需要的时间相对较短.此外,当Vs足够大时,即使处于稳态,f在一段时间内仍然存在波动,且Vs越大,波动越频繁,持续时间越长,如与Vs=20mV相比,当Vs=30mV时峰放电频率曲线更为波动.

图4 改进的LIF模型在不同强度交流外电场作用下的动态响应(a)膜电位曲线;(b)峰放电频率曲线.(fin=40Hz,A0=0mV)Fig.4 Dynamic responses of modified LIF model under the AC electric field with different strength.(a)membrane potential curves;(b)spike - frequency curve.(fin=40Hz,A0=0mV)
图5为改进的LIF模型在不同强度交流外电场作用下峰放电频率曲线.在一定Vs范围内,Vs相对较小时,起始峰放电频率曲线f0(Vs,A0)近似,且随着适应性变量初值A0的增加,起始峰放电频率曲线f0(Vs,A0)会沿着Vs增大的方向水平移动;而稳态峰放电频率曲线f∞(Vs)则在该Vs范围呈近似线性.但是当Vs增大到19mV后,f0(Vs,A0)曲线及f∞(Vs)曲线均呈现非线性.
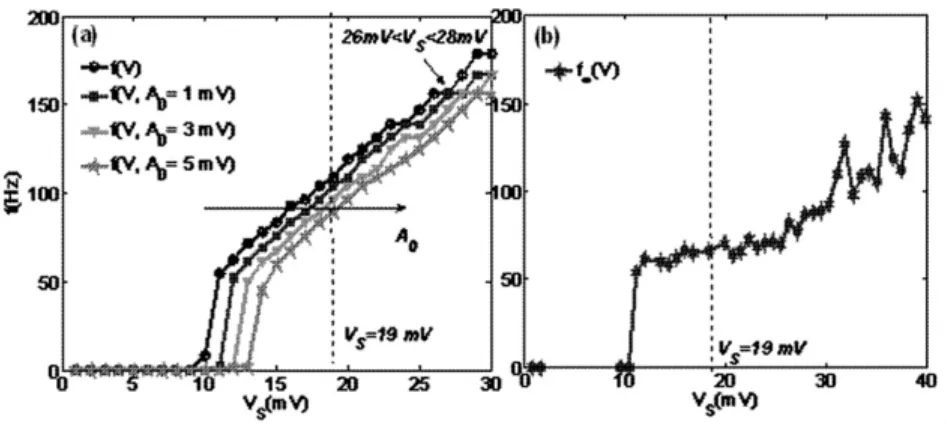
图5 改进的LIF模型在不同强度交流外电场作用下的峰放电频率曲线(a)起始峰放电频率曲线f0(Vs,A0);(b)稳态峰放电频率曲线.f∞(Vs)(fin=40Hz)Fig.5 Spike- frequency curves of modified LIF model under the AC electric field with different strength.(a)onset spike-frequency curve f0(Vs,A0);(b)steady state spike - frequency curve f∞ (Vs).(fin=40Hz)
图6为改进的LIF模型在不同强度交流外电场作用下相邻ISI相关性曲线.仿真结果表明,若Vs较小时,随着Vs的增强,相邻ISI相关性|CC|升高;当Vs增大至19mV时,随着Vs的增强,|CC|降低;当Vs增大到一定强度,|CC|趋于饱和.因此,当外电场强度Vs过大时,改进的LIF模型适应性会变差.这是由于在神经元峰放电过程中刺激强度波动导致的,外电场强度越强,波动越剧烈,适应性就越差.

图6 改进的LIF模型在不同强度交流外电场作用下相邻ISI相关性Fig.6 Correlation between successive ISI of modified LIF model under the AC electric field with different strength
2.2 不同频率交流外电场对改进的LIF模型的影响
为研究不同交流外电场频率对改进LIF模型的影响,首先,令交流外电场强度为定值Vs=20mV.仿真结果如图7所示,当交流外电场频率fin=8Hz时,起始峰放电频率f0=38Hz;当fin=24Hz时,f0=100Hz.随着时间的演化,峰放电频率f逐渐衰减至稳态峰放电频率f∞.此外当fin较低时,峰放电频率曲线f(t)会存在一定程度的波动,fin越低,f(t)曲线波动越频繁,持续时间越长.
图8为改进的LIF模型在不同强度交流外电场作用下峰放电频率曲线.随着fin的增加,f0随之增加.当A0增加时,起始峰放电频率曲线f0(fin,A0)会沿着fin增大的方向水平移动,并且在一定fin取值范围内,不同A0时,各f0(fin,A0)曲线斜率近似;当fin足够大时,稳态峰放电频率曲线f∞(fin)呈线性变化.
图9为改进的LIF模型在不同频率交流外电场作用下相邻ISI相关性曲线.随着fin的不断增大,相邻ISI相关性|CC|首先升高,然后逐渐降低,当fin>20Hz时,|CC|升高.因此,交流外电场频率越高,改进的 LIF 模型适应性越好.Benda[23]等人提出在刺激信息传递过程中,刺激的平均信息被移除,而快速波动信息被传递.这是外电场频率越高,适应性越好的主要原因之一.
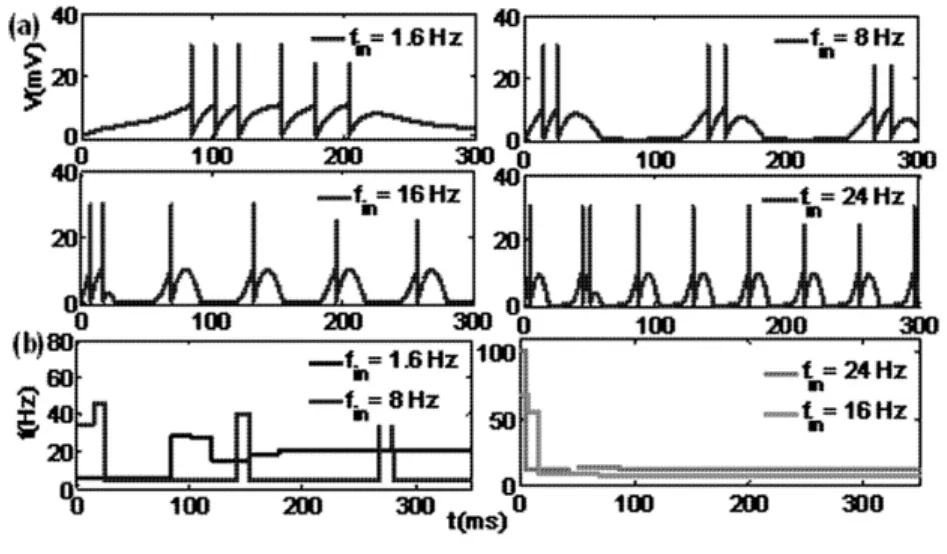
图7 改进的LIF模型在不同频率交流外电场作用下的动态响应(a)膜电位曲线;(b)峰放电频率曲线.(Vs=20mV,A0=0mV)Fig.7 Dynamic responses of modified LIF model under the AC electric field with different frequency.(a)membrane potential curves;(b)spike-frequency curve.(Vs=20mV,A0=0mV)

图8 改进的LIF模型在不同频率交流外电场作用下的峰放电频率曲线(a)起始峰放电频率曲线f0(fin,A0);(b)稳态峰放电频率曲线.f∞(fin)(Vs=20mV)Fig.8 Spike- frequency curves of modified LIF model under the AC electric field with different frequency(a)onset spike-frequency curve f0(fin,A0);(b)steady state spike-frequency curve .f∞(fin)(Vs=20mV)
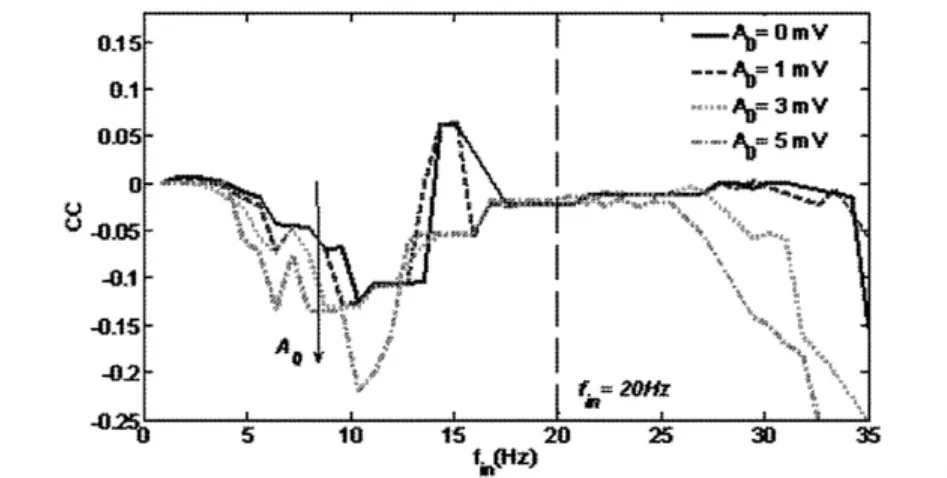
图9 改进的LIF模型在不同频率交流外电场作用下相邻ISI相关性Fig.9 Correlation between successive ISI of modified LIF model under the AC electric field with different frequency
3 结论
本文通过数值仿真,基于膜电位、峰放电频率、初始峰放电频率、稳态峰放电频率以及相邻ISI相关性等研究发现,LIF模型在交流外电场作用下呈现峰放电频率适应性,并且交流外电场的强度和频率均对适应性产生影响.外电场强度越小,频率越大,适应性越好.本文的研究结果为探索外电场对生物神经系统的影响以及一些神经系统疾病的物理治疗提供思路.
1 Michaelis B,Chaplain R A.Ion conductance changes associated with spike adaptation in the rapidly adapting stretch receptor of the crayfish.Plugers Arch,1975,354(4):367~377
2 Sawczuk A,Powers R K,Binder M.Spike frequency adaptation studied in hypoglossal motoneurons of the rat.J Neurophysiol,1995,73(5):1799~1810
3 Lancester B,Nicoll R A.Properties of two calcium-activated hyperpolarizations in rat hippocampal neurons.J Physiol,1987,389:187 ~203
4 Barkai E,Hasselmo M.Modulation of the input/output function of rat piriform cortex pyramidal cells.J Neurophysiol,1994,72(2):644~658
5 Ahmed B,Anderson J,Douglas R,et al.Estimates of the net excitatory currents evoked by visual stimulation of identified neurons in cat visual cortex.Cereb Cortex,1998,8(5):462~476
6 Brownstone R M,Krawitz S,Jordan L M.Reversal of the late phase of spike frequency adaptation in cat spinal motoneurons during fictive locomotion.Journal of Neurophysiology,2011,105(3):1045~1050
7 Avoli M,Olivier A.Electrophysiological properties and synaptic responses in the deep layers of the human epileptogenic neocortex in vitro.J Neurophysiol,1989,61(3):589~606
8 Lorenzon N M,Foehring R C.Relationship between repetitive firing and afterhyperpolarizations in human neocortical neurons.J Neurophysiol,1992,67(2):350 ~363
9 Vandecasteele M,Deniau J M,Venance L.Spike frequency adaptation is developmentally regulated in substantia nigra pars compacta dopaminergic neurons.Neuroscience,2011,192:1~10
10 Fernandez F R,Broicher T,Truong A,et al.Membrane voltage fluctuations reduce spike frequency adaptation and preserve output gain in CA1 pyramidal neurons in a high-conductance state.The Journal of Neuroscience,2011,31(10):3880~3893
11 Cortes J M,Marinazzo D,Series P,et al.The effect of neural adaptation on population coding accuracy.Journal of Computational Neuroscience,2012,32(3):387~402
12 Sobel E C,Tank D W.In vivo Ca2+dynamics in a cricket auditory neuron:an example of chemical computation.Science,1994,263(5148):823~826
13 Wang X J.Calcium coding and adaptive temporal computation in cortical pyramidal neurons.J Neurophysiol,1998,79(3):1549~1566
14 Peron S,Gabbiani F.Spike frequency adaptation mediates looming stimulus selectivity in a collision-detecting neuron.Nat Neurosci,2009,12(3):318~326
15 Brown D A,Adams P R.Muscarinic suppression of a novel voltage-sensitive K+ current in a vertebrate neuron.Nature,1980,283(5748):673~676
16 Sah P.Ca2+ -activated K+currents in neurones:types,physiological roles and modulation.Trends Neurosci,1996,19(4):150~154
17 Wang X J ,Liu Y,Sanchez-Vives M V,et al.Adaptation and temporal decorrelation by single neurons in the primary visual cortex.J Neurophysiol,2003,89(6):3279 ~3293 18 Lapicque L.Quantitative investigations of electrical nerve excitation treated as polarization.Biol Cybern,2007,97(5-6):341 ~349
19 Stein R B.A theoretical analysis of neuronal variability.Biophys J,1965,5(2):173~194
20 焦贤发,王俊琦,王如彬.突触噪声作用下的IF阈值神经元模型的随机共振.动力学与控制学报,2010,8(3):273~276(Jiao X F,Wang J Q,Wang R B.Stochastic resonance of an integrate and fire neuron model with threshold driven by synaptic noise.Journal of Dynamics and Control,2010,8(3):273 ~276(in Chiniese))
21 Treves A.Mean-field analysis of neuronal spike dynamics.Network:Comput Neural Syst,1993,4(3):259 ~284
22 Gigante G,Giudice P D,Mattia M.Frequency-dependent response properties of adapting spiking neurons.Math Biosci,2007,207(2):336 ~351
23 Benda J,Maler L,Longtin A.Linear versus nonlinear signal transmission in neuron models with adaptation currents or dynamic thresholds.J Neurophysiol,2010,104(5):2806~2820
24 Benda J,Hennig R M.Spike-frequency adaptation generates intensity invariance in a primary auditory interneuron.J Comput Neurosci,2008,24(2):113 ~136
25 Rauch A,Camera G L,Lüscher H R.Neocortical pyramidal cells respond as integrate-and-fire neurons to in vivolike input currents.J Neurophysiol,2003,90(3):1598 ~1612
26 Lapicque P E,Richmond B J,Nelson P G.Intrinsic dynamics in neuronal networks.II.experiment.J Neurophysiol,2000,83(2):808~827
27 Huang K M ,Li Y.The dynamic principle of interaction between weak electromagnetic fields and living system-Interference of electromagnetic waves in dynamic metabolism.Chinese J Med Phys,1997,14(4):205~207
28 Eichwald C,Kaiser F.Model for external influences on cellular signal transduction pathways including cytosolic calcium oscillations.Bioelectromagnetics,1995,16(2):75~85
29 Huang C M,Xu B Q,Lin J R.Effects of extremely low frequency magnetic fields on hormone-induced cytosolic calcium oscillations.Acta Biophys Sin,1999,15:543 ~546
30 Durand D M,Bikson M.Suppression and control of Epileptiform activity by electrical stimulation:A review.Proc of the IEEE,2001,89(7):1065~1082
31 Gluckman B J,Neel E J,Netoff T I,et al.Electric field suppression of epileptiform activity in hippocampal slices.J Neurophysiol,1996,76(6):4202~4205
32 Kringebach M L,Jenkisnson N,Owen S L F,et al.Translational principles of deep brain stimulation.Nature Reviews Neuroscience,2007,8(8):623~635
33 Ghai R,Durand D.Effects of applied electric fields on low calcium epileptiform activity in the CA1 region of rat hippocampal slices.J Neurophysiol,2000,84(1):274 ~280
34 Ebert U,Ziemann U.Altered seizure susceptibility after high-frequency transcranial magnetic stimulation in rats.Neurosci Lett,1999,273(3):155 ~158
35 Benda J,Herz A V M.A universal model for spike-frequency adaptation.Neural Comput,2003,15(11):2523~2564
36 Brette R,Gerstner W.Adaptive exponential integrateand-fire model as an effective description of neuronal activity.J Neurophysiol,2005,94(5):3637 ~3642
37 Crook M,Ermentrout G B,Bower J M.Spike frequency adaptation affects the synchronization properties of networks of cortical oscillators.Neural Computation,1998,10(4):837~854
38 Ermentrout B,Pascal M,Gutkin B.The effects of spike frequency adaptation and negative feedback on the synchronization of neural oscillators.Neural Comput,2001,13(6):1285~1310
39 Ermentrout B.Linearization of F-I curves by adaptation.Neural Comput,1998,10(7):1721~1729
*The project supported by the National Natural Science Foundation of China(61104032,61072012,61172009,50907044)and the Research Program of Tianjin University of Technology and Education(KYQD11005)
† Corresponding author E-mail:jiangwang@tju.edu.cn
SPIKE-FREQUENCY ADAPTATION IN THE MODIFIED LEAKY INTEGRATE-AND-FIRE MODEL UNDER EXTERNAL ELECTRIC FIELD*
Han Chunxiao1Wang Jiang2†Chang Li2Che Yanqiu1
(1.School of Automation and Electrical Engineering,Tianjin University of Technology and Education,Tianjin300222,China)(2.School of Electrical and Automation Engineering,Tianjin University,Tianjin300072,China)
Spike-frequency adaptation is a prominent property of neuronal dynamics in neural information processing.The external electric field has effect on the generation and conduction of neural information,and the dynamic behaviors of the neural system.Based on the leaky integrate-and-fire(LIF)model,a modified LIF model under the external electric field is established.From the membrane potential curve and the spike-frequency curve along with the time evolution process,the onset spike-frequency curve and the steady state spike-frequency curve along with the external electric field changes,and the correlation between successive inter-spike intervals(ISIs),the effect of external electrical field with different strength or frequency on the adaptability of the proposed model is discussed.
spike-frequency adaptation, external electric field, Leaky integrate-and-fire model, ISI,correlation
16 August 2012,
13 September 2012.
10.6052/1672-6553-2013-008
E-mail:jiangwang@tju.edu.cn步活动的影响,发现弱外电场能够完全抑制癫痫发作间簇放电[31];Ghai等人研究外生直流电场对自发低Ca2+簇放电的影响,增强刺激强度会对簇放电产生抑制作用[33];Ebert等人通过TMS研究低频刺激对大鼠杏仁核点燃发作的敏感性,发现经过低频TMS刺激,会在停止刺激后很长一段时间抑制癫痫[34].

