三维六角形编织结构的计算机模拟

高彦涛，KO Frank，胡 红，3

（1.东华大学 纺织学院，上海 201620；2.英属哥伦比亚大学 材料系 ＆先进材料工程工艺实验室，温哥华 V6T1Z4；3.香港理工大学 纺织与服装系，香港）

三维六角形编织结构的计算机模拟

高彦涛1，KO Frank2，胡 红1，3

（1.东华大学 纺织学院，上海 201620；2.英属哥伦比亚大学 材料系 ＆先进材料工程工艺实验室，温哥华 V6T1Z4；3.香港理工大学 纺织与服装系，香港）

基于三维六角形编织原理，采用编织纱线位置点的矩阵表示法，根据纱线的运动情况，得到每一步运动后的纱线位置坐标，然后采用B－spline曲线对每一根纱线进行拟合，用管状实体代表纱线对整个编织体进行三维显示，经过优化后得到编织体的仿真图像.仿真结果表明，该模拟方法能够对复杂六角形编织结构进行形象模拟，为探索编织体中内部纱线排布提供有力工具.

六角形编织；B－spline曲线；模拟仿真；Matlab编程

新型三维六角形编织是一种旋转编织方法，它能够编织多种复杂形状结构件，以及利用几十微米纱线进行微观精细化编织［1－4］，其产品在生物医用以及复合材料领域具有较大应用潜力.这种六角形编织与传统的纵横编织原理不同，因此，纵横编织的模拟方法不适用于六角形编织.文献［5－7］详细阐述了基于传统纵横编织原理得到的编织体的模拟方法，为了实现三维模拟仿真，它们都联合多种编程软件，通过一些文件修改与传递进行反复模拟，这给模拟的灵活性带来一定问题.

基于数学算法并利用Matlab编程，本文建立了一种针对六角形编织的模拟方法.一些新算法很容易加入模拟程序，易于进一步优化.同时，该方法可以进一步扩展到其他编织方法的模拟仿真，也适用于单胞模型的建立，对编织结构的研究有一定意义.

1 三维六角形编织的基本原理

旋转编织是通过控制凸轮旋转以及卷取机理来获得编织结构的方法.三维六角形编织是由Frank Ko教授发明的一种新型旋转编织［2］.事实上，控制凸轮的运动是为了移动载纱器使它在轨道板上运动来使纱线缠绕.为了得到需要的编织结构，在进行编织之前，必须确定携纱器（编织纱）的初始位置、凸轮的运动和卷取速度.

图1通过两个相邻六角形凸轮的3步连续运动描述了六角形编织基本原理.图1中3个不同标号的圆圈分别代表进行编织的3根纱线，凸轮的旋转模式由凸轮轴边上的旋转箭头表示.其中，图1（a）代表编织纱的初始位置，图1（b）～1（d）分别表示凸轮步进一次后编织纱的位置.从图1（b）可以看出，经过左边六角形凸轮逆时针旋转后，纱线1和2分别按照逆时针移动了一个位置.依次类推，可得到纱线在底盘的运动规律.

图1 三维六角形编织工艺示意图Fig.1 Schematic of 3Dhexagonal braiding process

2 三维六角形编织命令文件与编织纱的矩阵表示

为获得需要的编织结构，必须根据编织结构的要求确定电机运转.电机的运转模式保存于一个.txt文件，即指令文件，该文件包含编织机上所有凸轮每一步运动信息.指令文件包括两部分：一是机器卷取速度；二是电机运动模式.各个电机运动模式都是用数字表示，“1”代表顺时针旋转60°，“－1”代表逆时针旋转60°，“0”代表静止.一个用于编织管状结构的电机指令文件实例如图2所示.

图2中左侧第1和2列代表电机的定位，例如，motor 1－2代表第1圈第2个电机（凸轮）.从第3列开始的数字分别代表对应电机的运动模式，例如，motor 1－2后的3个数字分别为－1，－1，0，这表示motor 1－2在前两步编织时，逆时针旋转60°，第3步静止不动，以此类推.假如某电机第n步运动状态为1，代表电机在第n步执行顺时针旋转60°.利用此方法就可以表达所有编织过程.

图2 电机指令文件Fig.2 Command file of motors

实现编织结构的三维模拟需要从电机指令文件出发，依据电机指令文件获取载纱器的初始位置，并将其存储起来，存储形式为一个两维矩阵.图3描述了编织纱线的矩阵表示形式.

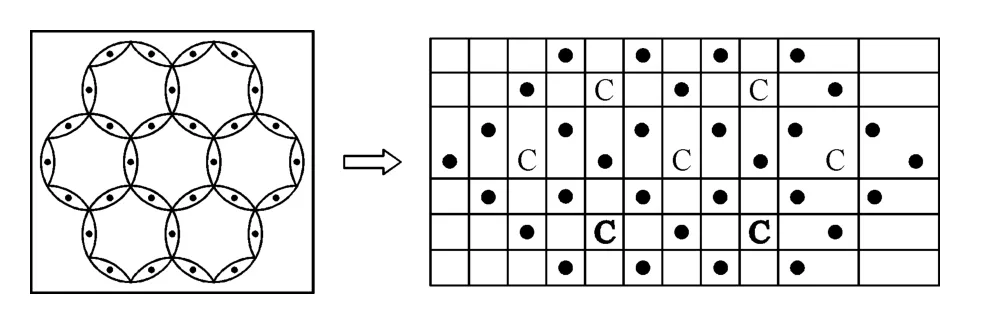
图3 编织纱的矩阵表示示意图Fig.3 Schematic of matrix representation of braiding yarn

依据图3中矩阵表示方法，在模拟编织过程中需要计算矩阵的纵行和横列数目，这两个参数在程序中分别用“nb＿row”和“nb＿column”表示，其值可由下列方程式给出：

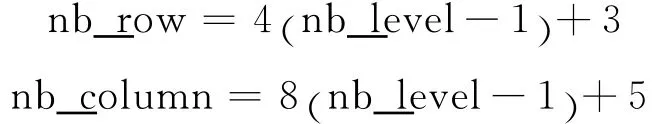
其中：nb＿level表示编织机器中凸轮的层数.

3 三维六角形编织的模拟方法

编织结构的模拟由编织工艺决定，三维六角形编织的主要工艺参数包括凸轮运动模式、编织尺寸、面板上携纱器布置形状等.为了正确地模拟编织结构首先必须得到这些工艺参数，其模拟的流程图如图4所示.

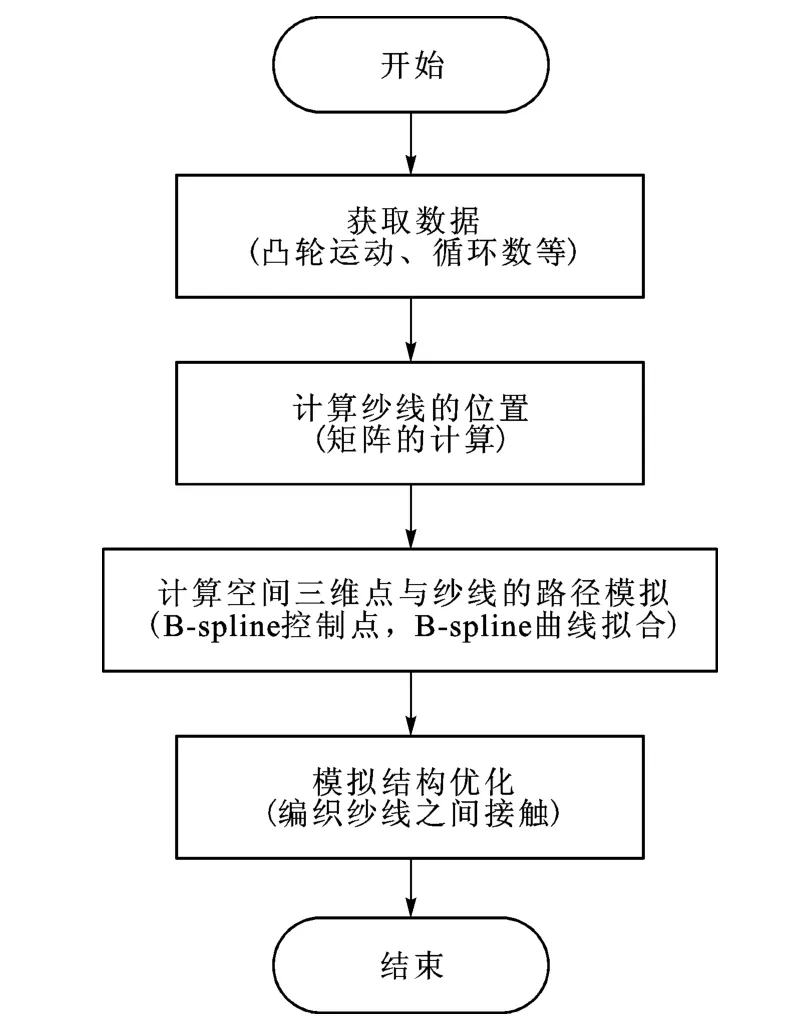
图4 三维六角形编织模拟流程图Fig.4 Flow chart of hexagonal braiding simulation

由图4可以看出，实现三维六角形编织模拟的主要过程包括4部分：编织工艺参数的读取；纱线位置的计算；创建B－spline曲线；模拟优化.

3.1 初始数据的读取

新型六角形编织是一种三维旋转编织，具有编织复杂形状的能力.为创造复杂结构，指令文件必须分别对每个电机独立控制.在进行编织模拟时，先读取指令文件.基于电机指令文件格式，编写相应程序来读取一些基本的编织参数，程序流程如图5所示.

3.2 计算纱线各步的位置

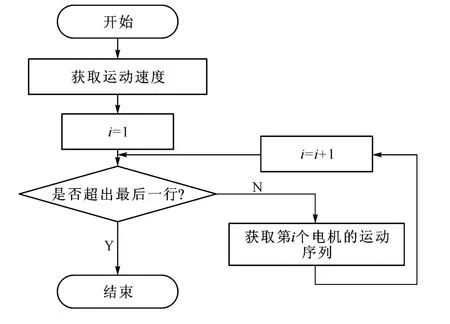
图5 数据读取流程图Fig.5 Flow chart of data acquisition

在考虑编织运动之前，必须先定义携纱器的初始位置.第一根纱线用数字“1”来表示，纱线总数为Nc.基于矩阵表示方法，可通过编写程序来实现各个纱线位置点分布.携纱器的初始位置确定以后，根据编织机每一步的运动情况就可以确定携纱器在每一步的位置.载纱器位置计算流程如图6所示.由图6可以看出，对于编织循环的每一步而言，必须考虑所有的凸轮转动.通过研究凸轮转动，建立起每步运动后携纱器在相应矩阵中的位置点.

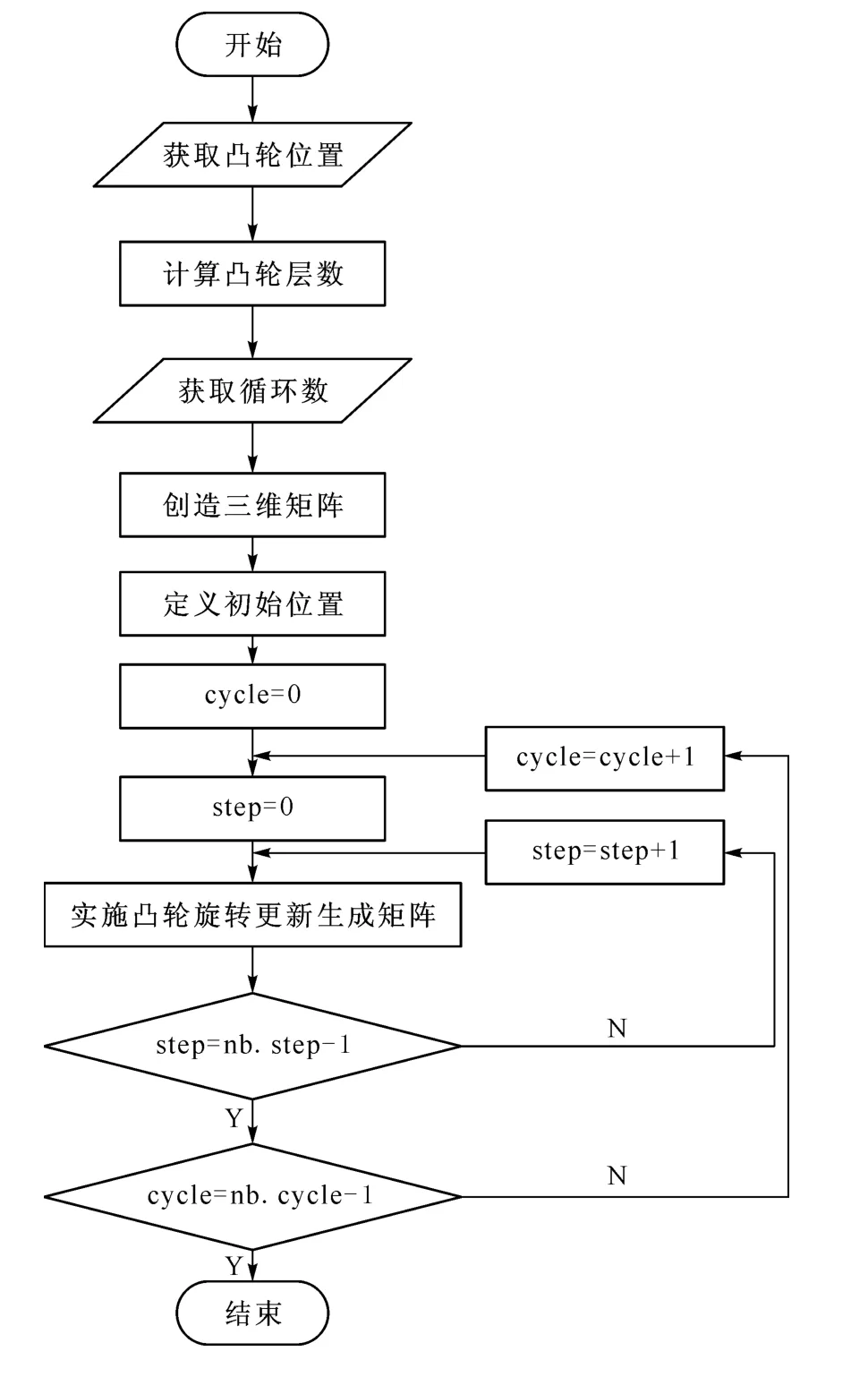
图6 携纱器位置计算流程图Fig.6 Flow chart of carrier position calculation

3.3 B－spline曲线的生成

图6中获得编织纱线矩阵给出了所有纱线在不同编织步的位置，基于这些数据可以画出每一根纱线沿编织方向延伸的位置.在模拟过程中，引入参数步长hstep，它表示两步编织之间的编织长度.3根纱线在空间的延伸路径模拟如图7所示.

图7 编织体中纱线路径Fig.7 Yarn paths in braid

由图7可知，编织纱线位置点延伸是由线段组成，它们不能用来代表纱线.为了使编织纱线在编织结构中平滑延伸，可利用B－spline曲线来拟合数据点，所得到的拟合曲线能够合理地代表纱线.为了定义B－spline曲线，必须确定3个参数（节点ti、控制点数f、曲线次数n）.依据这些参数，B－spline曲线可做如下描述.

首先，所有确定节点按如下方式排列：

同时定义一个整数：

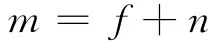
然后，B样条曲线可以写成如下形式：

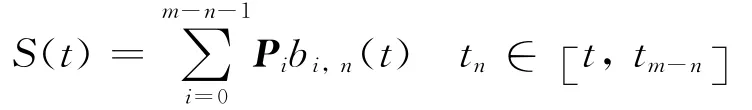
其中：Pi为控制点位置向量；

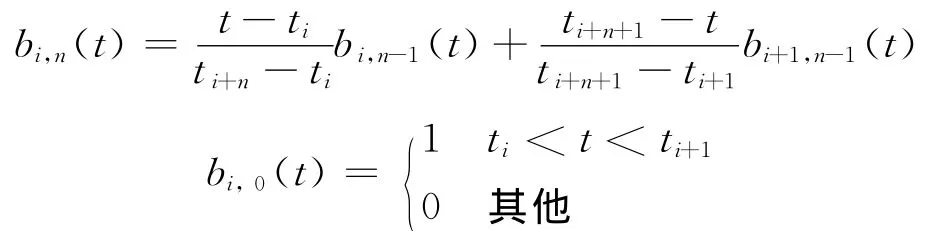
通过编写B－spline曲线模拟程序即可实现图7中对应于矩阵控制点的三阶样条曲线，如图8所示.

为了更加直观形象地描述纱线，由一个自定义函数tubeplot来实现纱线的管状实体显示.图8中的3根纱线利用此功能进行的管状实体表达形式如图9所示.

图8 编织纱线路径B－spline曲线拟合Fig.8 B－spline curve fitting of braiding yarn paths

图9 纱线的管状实体显示Fig.9 Description of braiding yarn using solid tube

3.4 优化过程

通过以上步骤，可以看出纱线编织后的缠绕方式，但是由于纱线之间没有接触，这不能代表纱线的真实位置.图10给出了一个优化前的编织体模拟图实例，可以看出纱线在编织体内没有相互接触.事实上，当进行编织时，由于纱线张力作用，纱线在编织体中趋向于走最短路径从而贯穿于整个编织体长度内，纱线会彼此接触紧挨在一起.因此，为了更好地模拟编织体，必须实施编织结构的模拟优化功能.

图10 优化前的编织体模拟图Fig.10 Simulation of a braid before optimization

通过改变各根纱线之间整体位置来实现编织结构的模拟优化，从第一根纱线开始，循环检查纱线间的距离，如果不相互接触，对B－spline曲线控制坐标乘一个系数来使纱线往编织结构中心靠近，直到纱线之间有接触.实现此功能的源代码如下：

在纱线坐标移动过程中，纱线的形状保持不变.优化前后的模拟编织结构对比如图11所示.由图11可以看出，经过优化之后的模拟图更能反映编织体的真实结构.

图11 优化前后编织结构模拟图对比Fig.11 Comparison of braid simulation before and after optimized process

不同结构形状的编织体模拟图如图12所示.由此可以看出本文方法能够较好地对三维六角形编织结构体进行模拟仿真，为研究编织体的内部结构提供了有力工具.

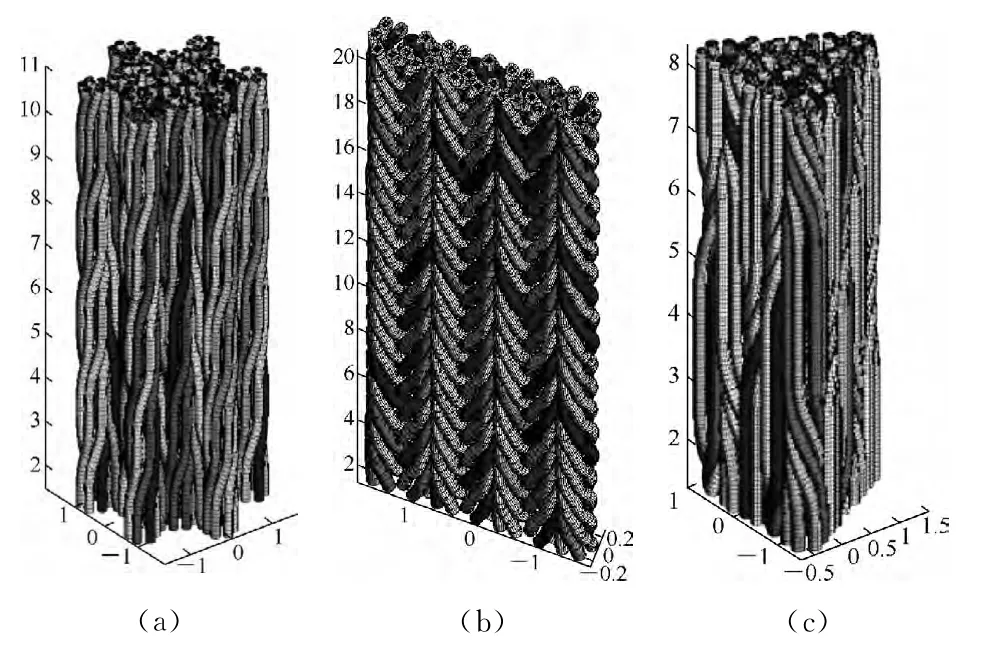
图12 不同形状的编织体模拟图Fig.12 Simulation of braided structures with different cross－sections

4 结 语

本文在分析三维六角形编织原理及编织过程的基础上，提出了编织过程中编织纱线矩阵表示方法.基于编织纱线的空间点矩阵，通过B－spline曲线拟合，实现了对编织体中纱线运动规律的模拟，并系统地介绍了这种基于Matlab编程的编织结构模拟方法.模拟得到的织物能够真实地反映了纱线在编织结构的运动规律，使得编织体内部结构可视化.

由于该模拟方法是利用基于数学方法的Matlab编程来实现，一些自定义新算法也可以施加在此模拟方法上，因此，该方法可以很容易扩展到其他编织方法的模拟仿真以及单胞模型的建立.

参 考 文 献

［1］BOGDANOVICH A E，MUNGOLOV D.Recent advancements in manufacturing 3－D braided preforms and composites［C］／／Proceedings of the Acun－4International Composites Conference.Sydney，Australia，2002：61－72.

［2］KO K F，SCHREIBER F，YANG H J，et al.Recent advancements in three dimensional braiding［C］／／Proceedings of the 1st World Conference on 3D－Fabrics and Their Applications.Manchester，UK，2008：10－11.

［3］SCHREIBER F，KO K F，YANG H J，et al.Novel three dimensional braiding approach and its application［C］／／17th International Conference on Composite Materials.Edinburgh，London：IOM Communications，2009：27－31.

［4］成铃.三维编织的计算机模拟技术［J］.天津工业大学学报，2001，21（2）：26－29.

［5］张美忠，李贺军，李克智.三维编织复合材料矩形预制件仿真［J］.航空学报，2006，27（5）：985－988.

［6］王毅强，张立同，成来飞.三维编织体复合材料空间几何结构的计算机模拟［J］.航空材料学报，2008，28（2）：95－98.

［7］邵将，温卫东，崔海涛.三维四步法编织复合材料结构的计算机仿真［J］.南京航空航天大学学报，2009，41（1）：36－40.

Computer Simulation of 3DHexagonal Braided Structures

GAOYan－tao1，KOFrank2，HUHong1，3
（1.College of Textiles，Donghua University，Shanghai 201620，China；2.Department of Material ＆AMPEL，University of British Columbia，Vancouver，BC V6T1Z4，Canada；3.Institute of Textiles and Clothing，The Hong Kong Polytechnic University，Hong Kong，China）

According to the principle of hexagonal braiding，yarns'positions at every step were obtained using matrix representation based on carrier movements.B－spline curve of each yarn was fitted through their spatial positions and yarns in braid were described as solid tubes.Finally，the 3D braids could be vividly simulated after optimization process.The simulation results show that the method is suitable for complicated structures，and provides a useful tool for investigating yarn's arrangements in braids.

hexagonal braiding；B－spline curve；simulation；Matlab programme

TB 332

A

1671－0444（2013）06－0785－05

2012－10－31

高彦涛（1984—），男，河南商丘人，博士，研究方向为纺织结构复合材料.E－mail：dhytgao＠hotmail.com

胡 红（联系人），男，教授，E－mail：huhong－dhu＠hotmail.com