基于鳞片纹图特征的羊绒识别及其含量确定
谢瑾仁,于伟东
(东华大学 纺织学院,上海 201620)
基于鳞片纹图特征的羊绒识别及其含量确定
谢瑾仁,于伟东
(东华大学 纺织学院,上海 201620)
毛发的鳞片纹图具有特征性,是人们区别不同毛发的重要特征之一,也是目前对羊绒/羊毛混合体鉴别及其含量测量的唯一标准方法.由于识别与计数为人工目测,易存在主观误差,故采用自制的光学显微成像系统获得图像进行图像处理与分析,提取羊绒和羊毛的纤维直径、鳞片高度、周长、面积、鳞片相对面积、鳞片相对周长、径高比和鳞片方形度共8个特征参数,并对各特征参数的相关性及分布特征进行研究讨论.试验结果表明,相对独立的特征参数为纤维直径、鳞片高度和方形度;羊绒与羊毛各参数理论分布曲线间的交叠面积最小为鳞片相对面积,这成为特征参数选择和判识概率计算中权系数确定的依据.最后采用多参数贝叶斯分类模型实测3种试样中羊绒和羊毛纤维含量,结果显示与试样的名义混纺比基本一致,从而证明此方法具有实用、精准、快速的特点.
毛发鳞片;纹图特征;混纺比;贝叶斯分类模型;图像处理
动物毛发纤维外表的鳞片形状(又称纹图)具有特征性[1].已有研究证明鳞片的纹图特征可以用于动物间的区别[2]和毛发纤维的区别[3].现实中,羊绒与羊毛混纺制品的纤维识别及羊绒含量的计算,就是依据各自鳞片纹图的差异进行人工识别或计算机识别[4-5],所判定的主要依据是鳞片的环状化[6],以及纤维直径、鳞片高度、鳞片厚度等几个指标[7-8].人工识别虽然有环状化的依据及综合性的判定,但相对计算机识别,其不仅耗时费力,主观性大,而且干扰多、误差大.本文采用光学显微成像分析系统采集纤维图像,经图像处理与分析以识别纤维表面鳞片图纹的差异[9],同时运用8个特征参数的多参数组合的贝叶斯模型[10]识别羊绒和羊毛,并计算羊绒/羊毛混纺织物中羊绒的含量,进而验证纤维鳞片纹图特征的指纹性.
1 试验部分
1.1 试验材料
试样1:咖啡色机织物,其羊绒/羊毛含量为30.2%/69.8%,经纬纱的纤维组成相同.
试样2:黑色机织物,其羊绒/羊毛含量为52.2%/47.8%,经纬纱的纤维组成相同.
试样3:驼色针织物,其羊绒/羊毛含量为90.03%/9.97%.
所有样品来自标准检验机构,称标准检验A.上述结果更接近于加工单位的名义混纺比,即工业加工中的工艺混纺比:试样1为30/70;试样2为50/50;试样3为100/0.
1.2 试验仪器
本试验所用的光学显微成像分析系统由东华大学纺织材料与技术实验室自主研发[11],其主要包括硬件机构、控制系统和图像处理软件3个部分.硬件机构主要包括多功能载物台、移动机构、显微数码摄像器、投影照明装置、计算机.该装置的显微成像系统主体如图1所示.该仪器的最大特点是可快速、无损地对纤维试样进行图像采集,即实物布样或衣样可直接放于该仪器载物台上,无需对测量样进行制样和其他处理.
1.3 试验流程
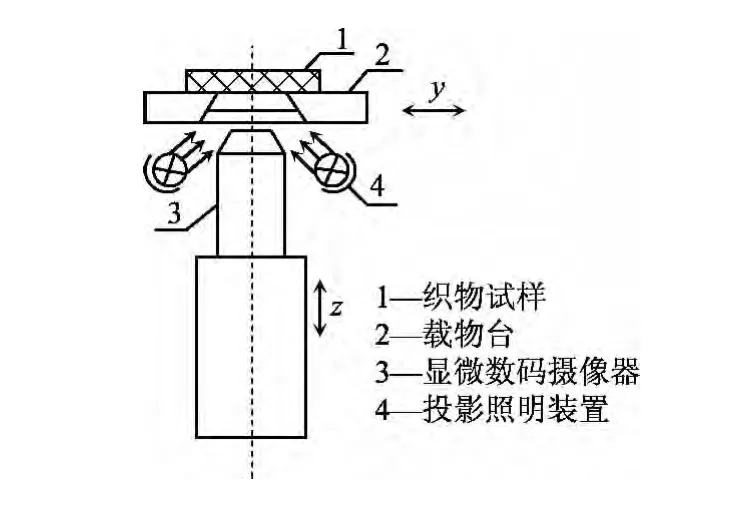
图1 显微成像系统主体图Fig.1 The main graphic of microscopic image system
试验的测试流程如图2所示.首先布样平置于载物台上,轻微加压,使布样平整地贴于玻璃窗上;调整光照角度和亮度,侧投射照明布样被检测面;显微数码摄像器的光学物镜和目镜的放大倍数分别为40和15倍,对每个试样沿x和y方向移动扫描采集,采集量为≥1 000根纤维图像,所采集的纤维鳞片图像如图3(a)所示.然后对图像作滤波和二值化处理,二值图像如图3(b)所示,采用Matlab对应工具箱完成8个特征参数提取.8个特征参数分别为纤维直径d(即鳞片宽度)、鳞片高度h、鳞片周长P、鳞片面积A、鳞片相对面积(面积比)Ad=A/d2、鳞片相对周长(周径比)Pd=P/d、鳞片相对高度(径高比)dh=d/h和鳞片的方形度SR=A/(P/4)2,涉及4个单一参数和4个组合参数.其中,方形度SR在文献[12]中定义为矩形度,但更为准确的定义应为鳞片方形化的程度,因为羊绒与羊毛在此特征上的区别是羊绒鳞片更为方形化.利用各参数分布函数的区别,建立多参数贝叶斯分类模型进行纤维识别,并根据识别出来的两类纤维根数计算其混纺比.
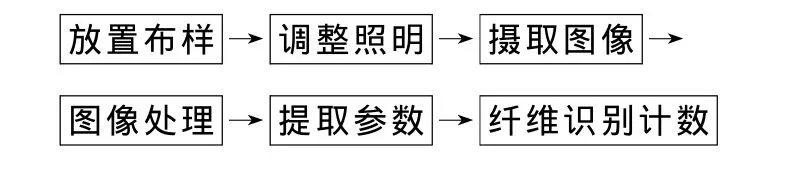
图2 试验纤维鳞片纹图特征提取分析流程图Fig.2 The flow diagram of fiber scale's feature extraction

图3 纤维原始图及二值图Fig.3 Original grey image of fiber and binary image of fiber
2 试验结果与分析
羊绒和羊毛都有鳞片,而鳞片纹图各具有特征性,这与人的指纹特征相类似[13].纤维鳞片的纹图复杂多变,故通过纤维鳞片的单一形状特征指标不可能清晰、准确地表达纤维的特征,因此,人们不会只以纤维直径或鳞片高度来区分羊绒和羊毛,而要观察羊绒和羊毛鳞片纹图的整体特征及其差异,或者利用某几个形态特征值来计算识别[14].这也是目前标准检验羊绒制品中羊绒含量的基础,只是测量与判断这些特征差异是依靠人工目测辨别来确定的.虽然纤维鳞片单一的形状特征理论上是随机的,但其分布特征是不同的.若多个纹图特征指标的分布特征放在一起考察,羊绒和羊毛的区别将是明显的,甚至完全不同的,即具有指纹性.基于这一事实,首先对本文所选择的8个特征参数的相关性和其分布特征值的差异性进行分析.
2.1 纤维鳞片纹图特征参数的相关性
光学显微成像分析系统对每个试样采集1 000根纤维图像,共3 000根纤维图像.对采集的纤维图像进行特征参数提取后,发现纤维各参数间的关系存在3种情况:线性相关、线性无关和非线性相关,分别见图4和5所示.

图4 3个试样的纤维参数间的线性相关和线性无关图Fig.4 The linear correlation and independence of parameters for 3samples
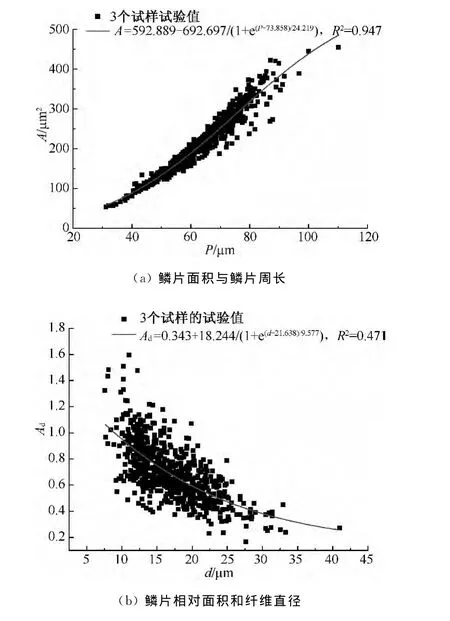
图5 3个试样的纤维参数间的非线性相关图Fig.5 The nonlinear correlation of parameters for 3samples
由图4(a)可知,3个试样的鳞片周长P随着纤维直径d的增加而增大,为典型的线性相关,相关系数R=0.871.此结果显而易见并存在正比关系P∝d,故其中一个参数独立,可选为识别指标.由图4(b)可知,3个试样的鳞片高度h与纤维直径d不存在相关性,其相关系数R=0.006,表明鳞片高度h独立于纤维直径d.
由图5(a)可知,3个试样的鳞片面积随着鳞片周长的增加呈非线性单调增加,相关度R2=0.947,故其更接近非线性相关,在纤维识别时只选其中一个参数即可.由图5(b)可知,3个试样的鳞片相对面积随着纤维直径的增加而呈非线性逐渐减小,其非线性拟合曲线的相关度R2=0.471,在纤维识别时只选其中一个参数即可.
由上述分析可知,试样中8个特征参数间的相关性差别较大,计算8个特征参数间的相关系数,如表1所示.由表1可知,纤维直径与鳞片高度和方形度为独立的,尤其方形度独立于其他7个参数,即鳞片纹图周长围起的图形方形化程度是表达羊绒和羊毛特征的独立参数.根据实际经验也知羊绒的鳞片径高比小于羊毛,只是人工很难综合方形度因子.直径与鳞片高度的相关系数仅为0.006,而与其他5个参数的相关系数较大.故将纤维直径作为一个固定识别指标,结合鳞片高度和方形度构成机检3参数识别模型.若不考虑各参数间的相关系数,可将8个参数都作为识别指标构成机检全参数识别模型.

表1 3个试样中纤维各特征参数间相关系数表Table 1 The correlation of characteristic parameters for 3samples
2.2 特征参数的分布特征值及差异
3个试样中纤维特征参数间不仅相关系数存在较大差异,其变异系数也同样存在差异,如表2所示.
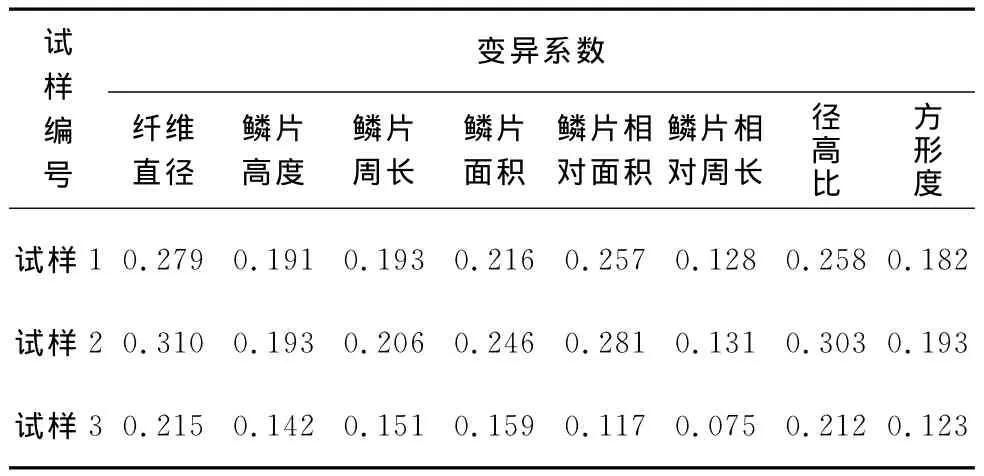
表2 3个试样中纤维各参数的变异系数Table 2 The coefficient of variation of characteristic parameters for 3samples
由表2可知,试样1和2中的纤维各特征参数的变异系数均大于试样3,且试样2又均大于试样1,表明羊绒和羊毛纤维存在显著差异,而3个试样中纤维直径的变异系数均为各参数中最大,故此参数识别纤维的能力强.
通过实测得到羊毛和羊绒两类纤维各1 000根的8个特征参数值,并经统计分布分析,可知羊绒和羊毛纤维的直径、鳞片高度、鳞片相对面积、鳞片相对周长、径高比和方形度近似服从对数正态分布,如图6所示.其中,方形度的分布重合度较高,而其他指标的分布差异较大,故用羊绒与羊毛同一参数的分布交叠面积Ac来表示识别的灵敏性,重合度越大,识别的灵敏性越差,如图6(a)中阴影部分所示.由于鳞片周长和鳞片面积的交叠程度最大,灵敏性差,故不列出两者的分布图.方形度SR虽为独立变量,但重叠面积很大,故识别的灵敏性也很差.



图6 羊绒与羊毛纤维6个参数的理论分布Fig.6 The theoretic distribution of the six parameters for cashmere and wool
由此分布结果讨论可知,两类纤维各参数的理论分布曲线的交叠部分是判定所测参数在区别羊绒和羊毛中是否显著的最重要依据.故引入正确判率参数a,如式(1)所示.

可以通过各参数理论分布曲线的非交叠性特征来确定各参数的选择,从而可知各参数识别纤维的显著性顺序为鳞片相对面积>鳞片径高比>鳞片相对周长>鳞片高度>纤维直径>鳞片方形度,即交叠面积越大,则识别纤维的显著性越差.由此可知,方形度的显著性很差,其识别纤维的能力很弱,故在主要影响参数识别模型的指标中,根据显著性排序,选择显著性最好的鳞片相对面积,且其与纤维直径和鳞片高度的相关系数也较小,从而构建了由纤维直径、鳞片高度和鳞片相对面积组成的3参数识别模型.现将羊绒和羊毛纤维的8个特征参数的统计值列出,如表3所示.
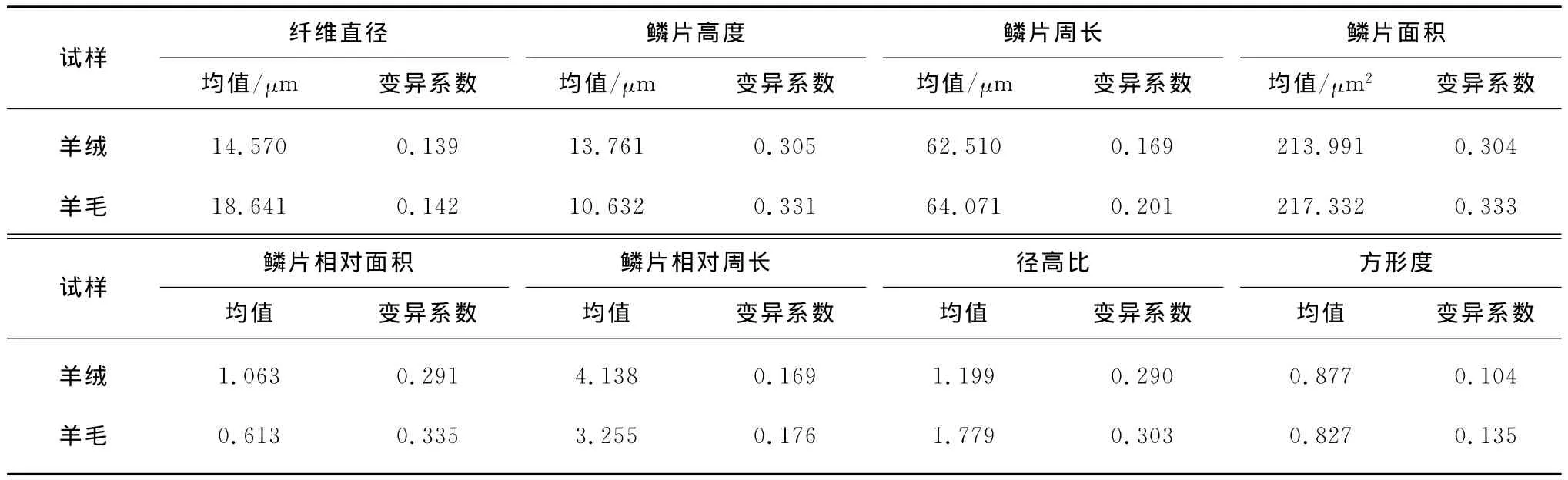
表3 羊绒和羊毛纤维中8个特征参数的统计值比较Table 3 The statistic comparison of 8characteristic parameters for cashmere and wool
由表3可知,羊绒的纤维直径、鳞片周长、鳞片面积和径高比的均值小于羊毛,而鳞片高度、鳞片相对面积、鳞片相对周长和方形度的均值大于羊毛.另外,羊绒纤维各参数的变异系数均小于羊毛纤维,且羊绒与羊毛纤维各参数的变异系数差异较大.对于单个参数而言,该参数的两类纤维均值差越大,变异系数差越小,以该参数判定时误差越小.
2.3 多参数贝叶斯分类模型及纤维识别
为了能辨识羊绒与羊毛纤维,利用两类纤维中提取的8个特征参数:纤维直径(x1)、鳞片高度(x2)、鳞片周长(x3)、鳞片面积(x4)、鳞片相对面积(x5)、鳞片相对周长(x6)、径高比(x7)以及鳞片方形度(x8),构成基于贝叶斯分类模型的多参数组合的识别.因此,每根纤维均可以用一个特征向量x=(x1,x2,x3,x4,x5,x6,x7,x8)表示.分别设羊绒纤维的条件值为ω1,羊毛纤维的条件值为ω2,则纤维的判别概率为P(ωi|x)(i=1,2),即每根纤维特征向量为x=(x1,x2,x3,x4,x5,x6,x7,x8)时,该纤维属于ωi条件的概率为P.
根据贝叶斯分类模型,得知其识别规则[15]:若P(ω1|x)>P(ω2|x),则判定此纤维为羊绒;若P(ω1|x)<P(ω2|x),则判定此纤维为羊毛.利用该识别规则对试样1,2和3中各1 000根纤维进行判定,计算出每根纤维的P(ω1|x)和P(ω2|x)值,分析每根纤维的种类,即可求得其混纺比.两类纤维的各参数的P(ωi|xj)(i=1,2;j=1,2,3,4,5,6,7,8)可以利用上文拟合的理论分布曲线求得,各曲线方程的函数表达式为

其中:σ和μ分别为理论分布曲线的均方差和均值;y0和A为拟合系数.
本文分别采用机检全参数模型和机检3参数模型对3个试样进行识别检测.取机检全参数模型,则依式(3)即可求得每根纤维的P(ω1|x)和P(ω2|x),并比较其大小判断每根纤维的种类.

其中:αj为权系数,其由各参数的正确判率aj依据式(4)得出的,而aj由式(1)求得.

由直径、鳞片高度和鳞片相对面积构成机检3参数模型,则P(ωi|x)=α1×P(ωi|x1)+α2×P(ωi|x2)+α3×P(ωi|x3),(i=1,2).
机检全参数模型和3参数模型对3个试样混纺比的测试结果如表4所示.

表4 3个试样的混纺比测试结果Table 4 The test results of blending ration for 3samples %
由表4可知,采用机检全参数模型和机检3参数模型所测得结果非常接近,由此说明筛选特征参数的重要性,这不仅可以准确地判定纤维的归属,计算得到各纤维的含量,而且可以减少和简化判别与计算量.标准检验A的结果与名义混纺比在试样1和2上最为接近,但在试样3(纯羊绒)上的羊毛含量竟为10.0%,由此可知试样1和2实测值接近名义值,而试样3的实测误差很大.因标准检验是通过拆纱、切成小段,混合后在显微镜下观察、判定和计数,所以采样偏差与人为误判会影响试验结果,其中标准检验B的结果较具有代表性.
显然本文方法的测试结果与名义混纺比更为接近,故表明依据特征参数建立贝叶斯模型对羊绒制品中羊绒纤维的识别更为精确,误判率更低,试样1的最大误判率仅为1.4%,试样2的最大误判率仅为1.6%,试样3的最大误判率为7.0%.尤其是试样3更能反映识别的绝对误差,标准检验A和B的误差分别为10.0%和8.0%,而本文方法的误差仅为6.8%,由此说明标准检验B本质上比标准检验A更为准确,但差于本文方法.
3 结 语
本文采用自制的光学显微成像分析系统,经图像处理和分析提取了羊绒和羊毛纤维的8个鳞片纹图特征参数,分析了各特征参数的相关性和其分布特征值的差异性,其中两类纤维各参数分布函数之间的差异是通过其理论分布曲线的交叠性特征来确定的.
提出了选择特征参数的两个依据:一是参数的分布曲线交叠面积越小,平均值的差异越大,变异系数差异越小,则应选为识别指标;二是参数的相关系数越小,即越独立,则应选为识别指标.根据两类纤维特征参数理论分布曲线的交叠面积引出了正确判率,它是所选参数的显著性和识别精度的基础,也构成了多参数贝叶斯分类模型中各特征值概率计算的权系数.
运用多参数贝叶斯分类模型的全参数和3参数模型,对3种试样进行识别,实测纤维含量与名义混纺比基本一致,这证明了参数筛选的重要性和本文中筛选方式的有效性.与实际标准检验方法比对,本文方法被证实更为精准、客观.
参 考 文 献
[1]石先军,于伟东,袁子厚.基于贝叶斯方法的山羊绒和细羊毛的鉴别[J].纺织学报,2008,29(1):26-28.
[2]SHE F H,KONG L X,NAHAVANDI S.Intelligent animal fiber classification with artificial neural networks[J].Textile Research Journal,2002,72(7):594-600.
[3]BAHUGUNA A, MUKHERJEE S K .Use of SEM to recognise Tibetan antelope (Chiru)hair and blending in wool products[J].Science &Justice,2000,40(3):177-182.
[4]JIA Y P,YANG Y H .Study on identifying blend ratio of wool and cashmere by computer image recognition technology [J].Energy Procedia,2011,13(6):8260-8266.
[5]ROBSON D,WEEDALL P J,HARWOOD R J.Cuticular scale measurements using image analysis techniques [J].Textile Res J,1989,59(12):713-717.
[6]杨桂芬,付妍,红霞,等.扫描电子显微镜与光学显微镜鉴别山羊绒纤维的技术探讨[J].中国纤检,2006(6):15-19.
[7]杨建忠,王荣武.羊绒与羊毛纤维表面形态的图像处理与识别[J].毛纺科技,2002(5):12-15.
[8]王晓红,姚穆,刘守智.绵羊毛与山羊绒的鉴别[J].西北纺织工学院学报,2001,15(2):204-206.
[9]季益萍,王瑞,杨锁廷,等.计算机图像识别技术检测羊绒羊毛混纺比[J].毛纺科技,2008(10):58-60.
[10]SHI X J,YU W D.Classification of animal fibers based on microscopic images[J].Journal of Applied Sciences,2009,27(1):62-66.
[11]于伟东,夏林,杜赵群,等.一种用于纺织品中纤维组成含量分析的装置及方法:中国,201010143828.4[P].2010-08-10.
[12]石先军.羊绒特征判析准则及快速识别算法研究[D].上海:东华大学纺织学院,2011.
[13]SHI X J,YU W D.Fuzzy classification of animal fibers using neuro-fuzzy classifier [C]//First International Conference on Intelligent Networks and Intelligent Systems.2008:119-122.
[14]张耀文.基于图像分析和统计分析的羊绒识别机制研究[D].北京:北京服装学院信息工程学院,2009.
[15]SHI X J,YU W D.A new classification method for animal fibers [C]//The 2008International Conference on Audio,Language and Image Processing.2008:206-210.
Using the Scale Pattern to Identify the Cashmere and Determine Its Content
XIEJin-ren,YUWei-dong
(College of Textiles,Donghua University,Shanghai 201620,China)
Scale pattern of hairs has the characteristic,it's one of the most important features to identify different hairs,it's also the only standard method used in the identification of cashmere/wool blends to obtain their blended ratio.There are some subjective errors due to the identification and counting of manual or visual checking,so a self-made optical microscopic imaging system is used for collecting images and image processing and analyzing,then 8 characteristic parameters are extracted,including fiber diameter,scale interval,scale perimeter,scale area,relative scale area,relative scale perimeter,relative scale interval,and scale square factor.The correlation and distribution among all the characteristic parameters are discussed.The experimental results show that fiber diameter,scale interval and scale square factor are relatively independent characteristic parameters,and the relative scale area has the minimal overlapping area of theoretic distribution in all parameters.The results become the basis of characteristic parameters selection and determining the weight coefficient of calculating identification probability.Finally,the multi-parameter Bayesian classification model is used in calculating content of cashmere and wool in 3 samples.The results are basically consistent,which proves that this method is feasible,accurate,and fast.
hair scale;pattern characteristic;blend ratio;Bayesian classification model;image processing
TS 102.3
A
1671-0444(2013)06-0737-07
2012-09-05
谢瑾仁(1989—),男,湖南邵阳人,硕士研究生,研究方向为纺织品检测和图像处理.E-mail:xiejinren890501@126.com
于伟东(联系人),男,教授,E-mail:wdyu@dhu.edu.cn

