一种综合的对流层延迟模型算法
杨 徉 喻国荣 潘树国 陈伟荣 汪登辉
(1东南大学交通学院,南京 210096)(2东南大学仪器科学与工程学院,南京 210096)
一种综合的对流层延迟模型算法
杨 徉1喻国荣1潘树国2陈伟荣1汪登辉1
(1东南大学交通学院,南京 210096)
(2东南大学仪器科学与工程学院,南京 210096)
摘 要:为了摆脱实测气象参数的限制,提升对流层延迟改正模型算法的普适性和效率,介绍了Saastamoinen模型、UNB3m模型、EGNOS模型3种常用的对流层延迟改正模型.在对3种模型的算法和模型参数进行介绍与分析的基础上,提出了一种综合的对流层延迟模型算法.该算法通过GPT模型估计出温度和气压参数,通过UNB3m模型估计水汽压参数,然后将计算得到的温度、气压和水汽压运用于Saastamoinen模型中以计算测站天顶对流层延迟.算法将GPT模型、UNB3m模型、Saastamoinen模型3种模型相结合,其精度与传统模型相当,但扩大了适用范围.该算法在缺少实测气象数据的情况下,能够较精确地给出对流层延迟的先验值,具有一定的实际工程意义.
关键词:GPT;UNB3m;Saastamoinen模型;对流层延迟模型
对流层指的是高度为40 km以下的大气底层,因其紧邻地表,大气稠密,所以对流运动在这层大气中最为显著,是热量传递的主要控制因子[1].电磁波通过对流层时,传播速度将产生变化,从而产生传播延迟.对流层延迟的90%是由大气中的干燥气体引起的,称为干分量;剩余10%是由水汽引起的,称为湿分量.对流层的折射与地面气候、大气压力、湿度和温度变化密切相关,这使得对流层折射比电离层更复杂,对流层折射的影响与信号高度角相关,在天顶方向,其影响为2.5 m左右,而当接近地平方向时,其影响可达25 m[2].所以对流层延迟的影响必须予以修正.
国内外的学者在这方面已经做了大量研究,提出了许多的改正模型,并且经过不断的优化,模型的改正效果也越来越好.常用的有 Hopfiled模型[3]、Saastamoinen 模 型[4]、UNB3m 模 型[5]、EGNOS模型[6]等,不同的模型有其相应的适用性.Hopfield和Saastamoinen模型需要测站位置的气象参数,但是一般测站不具备实测气象参数的条件,如果使用标准气象参数替代会降低模型的精度;EGNOS和UNB3m模型的适用范围小,全球范围内的模型精度不均匀.
因此,如何摆脱实测气象参数的条件,扩大模型的适用范围已逐步成为学者的研究热点.毛健等[7]通过天顶对流层延迟与测站经纬度、高程和年积日的关系分析中,提出了一种基于测站纬度、高程和年积日的全球对流层天顶延迟模型.姚宜斌等[8]也通过全球天顶对流层延迟格网时间序列研究,提出了基于球谐函数的全球非气象参数对流层天顶延迟改正模型.
本文在对现有模型算法的比较中,提出了一种新的对流层延迟模型算法,该算法在不丢失精度的同时,扩大了模型的适用范围,可应用于GNSS实时定位等领域.
1 常用的对流层延迟模型介绍
函数模型法是目前处理对流层延迟较为常用的方法,函数模型法基于“任意方向上的路径延迟均与天顶方向路径有关”的假设,将大气延迟误差写成天顶延迟改正与映射函数乘积的形式.本方法不仅计算简便,而且很好地解决了GNSS定位中由于解算路径延迟产生的方程秩亏问题.假定测站接收不同倾斜路径上的GNSS信号的对流层延迟是方位对称的,且可以投影到天顶方向上,基于这个假设,倾斜路径上的对流层延迟可表示为天顶方向的干、湿分量和相对应的投影函数:

式中,ΔDtrop为视线方向上的对流层延迟值;ΔDz,dry,ΔDz,wet分别为天顶对流层干、湿延迟值;Mdry(E),Mwet(E)为干、湿延迟对应的投影函数.
1.1 Saastamoinen 模型
Saastamoinen模型中,将对流层分成两层积分:地表到12 km左右高度对流层顶,其气体温度随高程变化的递减率假设为6.5℃/km;第二层是从对流层顶到50 km左右平流层顶,把大气温度假设成常数[9].
干分量和湿分量天顶延迟值可表示为

式中,e为水汽压;P为大气压力;T为温度.ZTD为天顶对流层延迟值.
1.2 UNB3m 模型
UNB3m模型天顶延迟模型中气象参数值是从海平面处起算,包括大气压P0(mbar)、温度T0(K)、水汽压e0(mbar)、温度变化率β(K/m)和水汽压变化率λ(mbar/m),这些气象参数以测站处的大地纬度和测量时间为依据,依照按照UMB3m对流层天顶方向干、湿延迟的气象参数格网值(表1和表2)进行内插求得,内插公式为
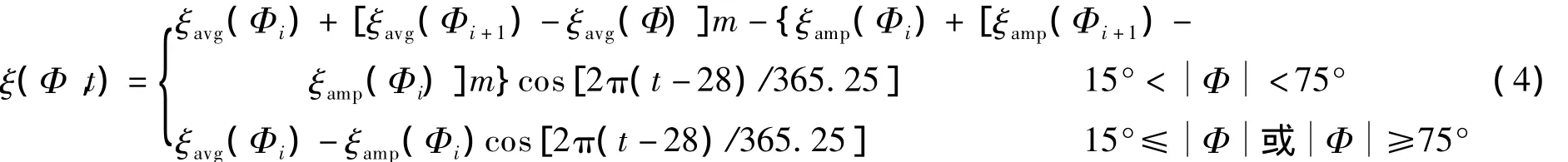
式中,m=(Φ -Φi)/(Φi+1-Φi),Φ 为测站处的大地纬度;Φi,Φi+1为与Φ相差最近的格网大地纬度;t为年积日;ξ为各参数的内插值.
在UNB3m模型中,水汽压e0需要通过内插后的大气相对湿度RH转换所得,计算出的水汽压为


UNB3m模型的干延迟和湿延迟为


式中,K1=77.60 K/mbar,K'2=16.6 K/mbar,K3=377 600 K/mbar,H 为高程,m;R=287.054 J/(kg·K),g=9.806 65 m/s2,gm=9.784(1 -2.66 ×10-3cos(2φ)-2.8 ×10-7H)m/s2,此外


表1 UNB3m模型干延迟气象参数格网值
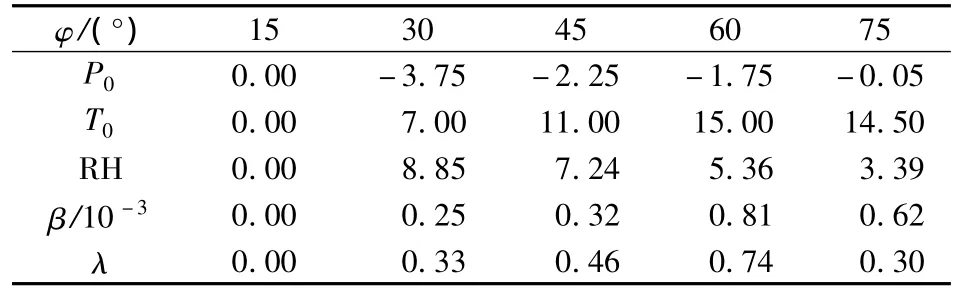
表2 UNB3m模型湿延迟气象参数格网值
1.3 EGNOS 模型
EGNOS模型也分为干延迟和湿延迟两部分,但映射函数只有一个,所以任意方向上的对流层延迟可以表示为

EGNOS由平均海平面的天顶延迟计算接收机处的天顶延迟为

式中,zwet和zdry为平均的海平面干延迟和湿延迟.

式中,K1=77.604 K/mbar,K2=382 000 K/mbar,gm=9.784 m/s2,P为平均海平面气压;e为平均海平面水汽压.
平均海平面的气象参数P,T,e,β,λ的计算公式如下:

式中,ξ0(φ)为各气象参数的年平均值;Δξ(φ)为各气象参数的季节变化率;Dmin为年变化的最小日期(北 半 球 Dmin=28,南 半 球 Dmin=211)[6].ξ0(φ),Δξ(φ)可由纬度范围内的全球平均海平面的各气象参数(见表3和表4)内插所得,内插方法与UNB3m的方法类似.

表3 EGNOS模型干延迟气象参数年平均值格网值

表4 EGNOS模型湿延迟气象参数季节变化率格网值
2 综合对流层延迟模型算法
通过对各种模型的分析,不难发现,如果有测站点比较准确的气象参数,利用Saastamoinen模型等都能对干分量做精度为毫米级的改正.经过文献的查阅,在处理对流层延迟方面,所有IGS分析中心都采用了GPT(global pressure and temperature)模型[10].GPT模型准确地描述了全球温度的年度周期变化,更适合在GNSS数据处理中使用.用GPT模型能估计出温度和气压2个气象参数,而UNB3m作为模型中精度较高的模型,可以通过UNB3m模型估计水汽压.然后将计算得到的温度、气压和水汽压运用到Saastamoinen模型中得到测站天顶对流层延迟.因此综合对流层延迟模型算法的思路如图1所示.

图1 综合对流层延迟模型算法流程
2.1 GPT模型计算测站温度和气压
GPT模型的输入值为测站经度、测站纬度、大地高和年积日.GPT模型的输出值为温度、气压和高程异常.
首先以9阶9次球谐函数求出测站位置温度与气压的年平均值a0、年变化幅度A和高程异常N.

式中,Pnm表示勒让德多项式;Anm和Bnm表示球谐函数的系数,通过ECMWF中心三年的分析数据和EGM96重力模型数据以最小二乘的方法解算得到;φ和λ表示测站的纬度和经度.然后在年平均值和年变化幅度的基础上,以余弦函数的形式求出具体某一年积日的温度与气压值.

式中,P0和T0表示平均海平面的温度与气压值;d表示年积日.最后根据测站高程进行梯度改正.
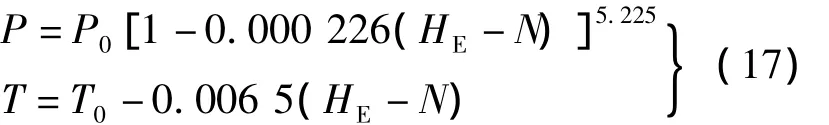
式中,P和T表示测站位置的温度与气压值;HE-N表示测站高于海平面的高度,即测站的正常高.
2.2 UNB3m模型计算测站的水汽压
参照2.2中式(4),通过测站的纬度和年积日,内插得到UNB3m模型天顶方向干、湿延迟的气象参数格网值,然后依据式(5)求解得测站水汽压e.
2.3 Saastamoinen 模型
将GPT模型计算得到的测站温度和气压,UNB3m模型计算得到的水汽压值e,代入式(2)、(3)即可得到测站天顶方向延迟值.
3 数据分析
采用一组采样自2011年12月29日24小时的测站BTLU的原始RENIX数据,考虑到卫星的可视性,选取一天中的2个时段(02:00—04:00和14:00—16:00),采样率为1 s.采用前文介绍的方法,分别利用 Saastamoinen模型、UNB3m模型、EGNOS模型及本文提出的模型算法求解得到天顶方向对流层延迟值,然后统一利用Neill模型[11-12]进行视线方向上的投影,计算测站视线上的对流层延迟值进行比较.得到图2和图3.从图像的对比,可以发现:
1)综合模型算法与现有的主要对流层模型相比,在数值上无明显的偏差,并且在趋势上无较大差异,说明综合模型算法本身具有一定的适用性.
2)综合模型算法得到的对流层延迟的值为EGNOS和UNB3m模型之间,延迟值随着高度角变化的趋势去其他模型近似,模型精度相仿.
3)综合模型算法同样无需利用实测气象数据得到对流层延迟值,计算方便.

图2 2:00—4:00模型估计对流层延迟随高度角变化图

图3 14:00—16:00模型估计对流层延迟随高度角变化图
4 结论
1)受对流层湿延迟和水平梯度延迟等复杂情况影响,经验模型计算对流层延迟无法做到非常精确,并且经典模型计算天顶对流层延迟的值非常接近.GPT/UNB3m融合Saastamoinen模型的对流层延迟综合模型算法有效保证了对流层延迟模型的精度,扩大了适用范围,计算过程中不再使用标准气象参数,充分体现了对流层延迟的时空变化特性.
2)本文提出的全球对流层延迟改正模型相比于北美UNB3m模型和欧洲EGNOS模型,提升了对流层延迟模型改正算法的普适性.在GNSS数据处理精度要求不是很高,但实时性要求很高的情况下,将模型值作为对流层延迟值参与计算,可以减少待估参数的个数,提高算法效率.因此,GPT/UNB3m融合Saastamoinen模型的对流层延迟综合模型算法具有实际应用价值.
3)模型的适用性需要通过更多的数据进行模验证、模型适用全球区域范围,这些问题是需要进一步的研究和分析.
[1]欧吉坤.GPS测量的中性大气折射改正的研究[J].测绘学报,1998(1):31-36.
Ou Jikun.Research on the correction for the neutral atmospheric delay in GPS surveying[J].Acta Geodaetica et Cartographic Sinica,1998(1):31-36.(in Chinese)
[2]杨力.大气对GPS测量影响的理论与研究[D].河南:解放军信息工程大学测绘学院,2001.
[3]Hopfield H S.Two-quartic tropospheric refractivity profile for correction satellite data[J].Journal of Geophysical Research,1969,74(18):4487-4499.
[4]Saastamoinen J.Contribution to the theory of atmospheric refraction[J].Bulletin Geodesique,1973,107(1):13-34.
[5]Leandro R F,Santo M C,Langly R B.UNB neutral atmosphere model:development and performance[C]//Proceedings of ION NTM 2006C.Monterey,USA,2006:564-573.
[6]刘靖晔,宋元明,胡加星.EGNOS对流层延迟改正模型及其精度分析[J].地理空间信息,2011,9(2):96-98.
Liu Jinye,Song Yuanming,Hu Jiaxing.EGNOS tropospheric delay model and its accuracy analysis[J].Geospatial Information,2011,9(2):96-98.(in Chinese)
[7]毛健,朱长青,郭继发.一种新的全球对流层天顶延迟模型[J].武汉大学学报:信息科学版,2013,38(6):684-688.
Mao Jian,Zhu Changqing,Guo Jifa.A new global zenith tropospheric delay model[J].Geomatics and Information Science of Wuhan University,2013,38(6):684-688.(in Chinese)
[8]姚宜斌,何畅勇,张豹,等.一种新的全球对流层天顶延迟模型 GZTD[J].地球物理学报,2013,56(7):2218-2227.
Yao Yibin,He Changyong,Zhang Bao,et al.A new global zenith tropospheric delay model GZTD[J].Chinese Journal of Geophysics,2013,56(7):2218-2227.(in Chinese)
[9]殷海涛.基于参考站网络的区域对流层4D建模理论、方法及应用研究[D].成都:西南交通大学土木工程学院,2006.
[10]Boehm J,Heinkelmann R,Schuh H.Short note:a global model of pressure and temperature for geodetic applications[J].Journal of Geodesy,2007,81(10):679-683.
[11]Niell A E.Global mapping functions for the atmospheric delay at radio wavelengths[J].Journal of Geophysical Research,1996,101(B2):3227-3246.
[12]胡伍生.GPS精密高程测量理论与方法及其应用研究[D].南京:河海大学水电学院,2001.
A comprehensive algorithm using fusion of tropospheric delay models
Yang Yang1Yu Guorong1Pan Shuguo2Chen Weirong1Wang Denghui1
(1School of Transportation,Southeast University,Nanjing 210096,China)
(2School of Instrument Science and Engineering,Southeast University,Nanjing 210096,China)
Abstract:In order to get rid of the restrictions of the actual measurement of the meteorological parameters and improve the universality and efficiency of tropospheric delay correction models,three types of tropospheric delay correction models are introduced,which are the Saastamoinen model,the UNB3m(university of new brunswick 3 modified)model and the EGNOS(the European geo-stationary navigation overlay system)model.The model algorithms and parameters are analyzed,and a comprehensive algorithm which is a fusion of the GPT(global pressure and temperature)model,the UNB3m model and the Saastamoinen model is put forward.In the proposed algorithm,the temperature and pressure parameters estimated through the GPT model and the vapor pressure parameter estimated through the UMB3m model are used to calculate the zenith tropospheric delay through the Saastamoinen model.Though the proposed algorithm is equivalent in precision to the conventional models,it has a wider scope of application.The algorithm can precisely provide the priori value of the tropospheric delay in the circumstances where measured meteorological data are absent,so it is of practical engineering significance.
Key words:GPT(global pressure and temperature);UNB3m(university of new brunswick 3 modified);Saastamoinen model;tropospheric delay model
中图分类号:P228.1
A
1001-0505(2013)S2-0418-05
doi:10.3969/j.issn.1001 -0505.2013.S2.043
收稿日期:2013-08-10.
杨徉(1991—),男,硕士生;喻国荣(联系人),男,博士,副教授,476310930@qq.com.
基金项目:国家自然科学基金资助项目(6522000013).
引文格式:杨徉,喻国荣,潘树国,等.一种综合的对流层延迟模型算法[J].东南大学学报:自然科学版,2013,43(S2):418-422.[doi:10.3969/j.issn.1001 -0505.2013.S2.043]
——环地平弧&环天顶弧

