基于蚁群优化算法的大跨度预应力混凝土桥梁挠度预测
黄 腾 陈喜凤 刘 岭
(1河海大学地球科学与工程学院,南京 210098)(2浙江省电力设计院,杭州 310012)
基于蚁群优化算法的大跨度预应力混凝土桥梁挠度预测
黄 腾1陈喜凤1刘 岭2
(1河海大学地球科学与工程学院,南京 210098)
(2浙江省电力设计院,杭州 310012)
摘 要:为了解决大跨径预应力混凝土桥梁挠度变形难以准确预测这一问题,提出采用适用于解决复杂、不确定性、非线性问题的蚁群优化算法.该算法中蚂蚁根据反映蚁群整体经验的信息函数和反映蚂蚁个体经验的启发函数计算转移概率,作为其进行路径选择的依据,然后根据所选路径的优劣释放一定浓度的信息素以增加蚁群整体的累积经验,由此形成正反馈、自催化的路径选择机制.基于此模型,结合某大跨径预应力混凝土桥梁挠度变形实际情况,将挠度变形量视为蚂蚁进行路径选择和释放信息素的基本依据,通过合理确定信息函数、启发函数、信息素更新策略、蚂蚁搜索及预测机制,构建了挠度变形预测的蚁群优化算法模型.对该桥梁跨中沉降槽部分2个不同阶段的挠度变形预测结果表明,该模型预测精度较高,适用性较强,为类似桥梁挠度预测开辟了一条新的途径.
关键词:蚁群优化;挠度预测;大跨径预应力混凝土桥梁;路径选择;信息函数;启发函数
相关研究发现,国内外很多大跨度预应力混凝土桥梁在投入运营一段时间后均出现了不同程度的病害,尤其是跨中持续下挠以及下挠量过大已成为大跨度预应力混凝土桥梁的世界性通病[1].图1为某大跨度预应力混凝土箱梁大桥2001~2012年跨中部分的挠度变化曲线,截至2012年4月,梁的最大挠度变形已达13.2 cm,形成了2个明显的沉降槽,且下挠趋势尚未完全收敛.

图1 某大跨度预应力混凝土箱梁大桥2001~2012年跨中部分挠度变化曲线图
大跨径预应力混凝土桥梁投入运营后,由于受混凝土收缩与徐变效应、温度、荷载等诸多因素的影响,难以建立较为精准的挠度预测模型.已有方法[2-5]通过考虑其中部分影响因子建立预测模型,取得了一定成效,但由于影响因子选取的人为干扰性较大,使得预测模型的性能不太稳定,普遍适用性较差.意大利学者Dorigo等[6]在1992年提出的蚁群优化算法是一种模拟自然界蚂蚁群体根据信息素寻找蚁穴到食物源的最短路径的群体智能算法,在解决复杂、不确定性、非线性问题上表现出明显的优势.其自组织机制使得算法不需要对所求问题的每一方面都有详尽的认识,这对于影响因素复杂的大跨径预应力混凝土桥梁挠度预测来说无疑是十分有利的,但目前还未见相关报道.本文将就这一问题展开尝试性的探索和研究.
1 蚁群优化算法的数学模型
蚁群优化算法[7-9](ant colony optimization)最早主要用于处理单一的旅行商问题(TSP),为便于理解,首先结合TSP问题来说明蚁群优化算法.
1.1 路径选择机制
设平面上有N座城市和m只蚂蚁,ηij(t)为城市i,j之间路径的可见度(又称启发函数),即路径(i,j)被选择的期望程度,dij表示城市 i,j之间的距离,一般定义

设τij(t)为路径(i,j)上残留信息素浓度(又称信息函数),初始时刻,各路径上信息素浓度相等,即τij(0)=C(C 为非零常数).蚂蚁 k(k=1,2,…,m)在运动过程中,根据各条路径上的信息函数τij(t)和启发函数ηij(t)计算状态转移概率Pkij(t),从而决定移动方向.t时刻位于城市i的蚂蚁k选择城市j的概率为

式中,allowedk表示蚂蚁 k允许选择的城市,allowedk={1,2,…,N}-tabuk,tabuk代表蚂蚁 k 已走过的城市,称禁忌表;s为蚂蚁k下一步所有可能选择的路径.α为信息启发因子,代表路径(i,j)上存在的信息素对蚂蚁选择路径的重要程度,体现了蚂蚁之间的协作性;β为期望启发因子,代表路径(i,j)的可见度对路径选择的影响程度,体现了蚂蚁个体的独立性.
1.2 信息素调节机制
蚂蚁重复地使用式(2)所示的决策从一个城市到达另一个城市,并在走完一步或遍历所有城市一次后,修改所经过路径的信息素浓度.为了避免路径上残留信息过多而淹没启发信息,使路径上的信息素随时间而挥发,以有效降低算法的停滞性[7].t+1 时刻边(i,j)上的信息素为

式中,Δτij(t)表示本次循环中路径(i,j)上信息素浓度的增量;Δ(t)表示第k只蚂蚁在本次循环中在路径(i,j)上留下的信息素;ρ为信息素挥发系数,取值范围为(0,1).Dorigo曾根据信息素更新方式的不同,提出了3种不同的基本蚁群算法模型[10].实际应用时应针对具体问题,选择恰当的信息素更新策略.
2 大跨度预应力混凝土桥梁挠度变形预测模型的构建与实现
2.1 路径选择机制
结合大跨径预应力混凝土桥梁挠度变形实际(见图1),建立与TSP蚁群算法模型类似的路径选择机制是准确构建预测模型的基础.将桥面测点视为TSP模型中的城市,挠度变形量视为蚂蚁进行路径选择和释放信息素的基本依据,蚂蚁倾向于朝挠度变形量大的方向移动.由此,某个测点的累积挠度变形量或该测点两侧一定邻域内测点的平均累积变形量可被视为反映蚁群整体累积经验的信息函数,而该测点相邻两期累积变形量之差即可被视为反映某只蚂蚁个体经验的启发函数,蚂蚁根据信息函数和启发函数计算转移概率,并根据所选路径的优劣更新信息素,以增加蚁群整体的累积经验,如此便形成了正反馈、自催化、自组织的路径选择机制.
2.2 信息函数和启发函数
2.2.1 初始信息函数 τij(0)
由图1可以看出,该桥运营前4年是挠度变形最为剧烈、跨中部分沉降槽的形成阶段.在该阶段可将桥梁某位置前两期挠度变形量之差作为其初始信息素浓度,对其稍作处理,定义

式中,ΔLj为测点j前两期累积挠度变形量之差;ΔLmin,ΔLsum分别为j点所在区段内各点前两期累积挠度变形量之差的最小值及和;Q为信息素浓度.可见,测点前两期累积挠度变形量之差越大,相应路径上的初始信息素浓度越高.
从图1还可看出,该桥运营4年后,沉降槽下挠变形速率减慢,将这一阶段称作沉降槽的发展阶段.该阶段决定路径上初始信息素浓度的主要因素是某位置的累积挠度变形量,因此定义

式中,Lj为测点j前期累积挠度变形量;Lmin,Lsum分别为j点所在区段内各点前期累积挠度变形量的最小值及和.式(6)表明,该阶段前期累积挠度变形越大的位置被选择的概率较高.
2.2.2 启发函数 ηij(t)
ηij(t)反映了蚂蚁在测点i选择测点j的期望,j点相对于i点的挠度变形越大,蚂蚁越倾向于选择j点.相应于上述沉降槽的形成和发展两个阶段,启发函数有以下2种定义:

2.3 信息素更新策略
在挠度预测模型中,测点的挠度情况决定蚂蚁的移动,信息素浓度的增量只与蚂蚁k每步移动的局部信息有关,因此,定义蚂蚁k从i点移向j点后,在路径(i,j)上释放的信息素如下:
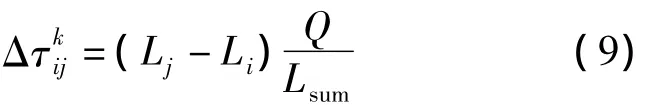
上式表明,蚂蚁释放信息素的多少与j点和i点之间累积挠度变形的差异有关.
综合考虑信息素的释放和挥发,t+1时刻路径(i,j)上的信息素浓度按式(3)~(4)调整.
2.4 蚁群的并行搜索机制
首先,根据桥梁挠度变形情况将全部测点分成若干区段,变形较大部分可以细分.分别在每一区段内放置若干只蚂蚁,其初始位置随机确定,尽量使其均匀分布在测段内的测点上.每只蚂蚁均配有一个禁忌表,用于存放蚂蚁已到达过的测点.然后,令所有蚂蚁按照前述路径选择机制和信息素更新策略进行并行搜索以及信息素的更新,自组织地进化算法.若蚂蚁的禁忌表已满却仍未达到终止搜索条件时,则清空禁忌表,进入下一个循环.终止搜索的条件可根据测点数量和预测精度适当调整,当区段内测点数量不多时,可将终止条件设置为所有蚂蚁都聚集到某一测点上;若区段内测点数量较多,可将终止条件设置为一定数量的蚂蚁聚集到某一测点上,另外也可通过设置搜索的最大循环次数终止搜索.
2.5 挠度预测机制
搜索终止后,各测点均记录了蚂蚁到达的频数,由于蚂蚁倾向于移向挠度变化量大的测点,因此,可通过建立频数与挠度变形量之间的对应关系来推算各测点的变形量.比较预测结果与实测数据,若预测偏差较小,则将预测数据作为已知数据继续进行后续预测,否则需考虑重新放置蚂蚁的初始位置或修改信息函数、启发函数、信息素更新策略等.
2.6 预测模型中参数的选取
以下几个参数直接影响预测模型的性能[7]:m,Q,α,β,ρ,其取值的确定需在全局搜索能力和收敛速度之间寻求最佳折中.由于算法参数空间的庞大性以及各参数之间的紧密关联性,目前尚无简单有效方法.本文大体参照“三步走”方法[11],按一定步长经多次试算确定.
2.7 模型实现的主要流程
按照上述算法构建大跨径预应力混凝土桥梁挠度预测模型的主要流程如图2所示.
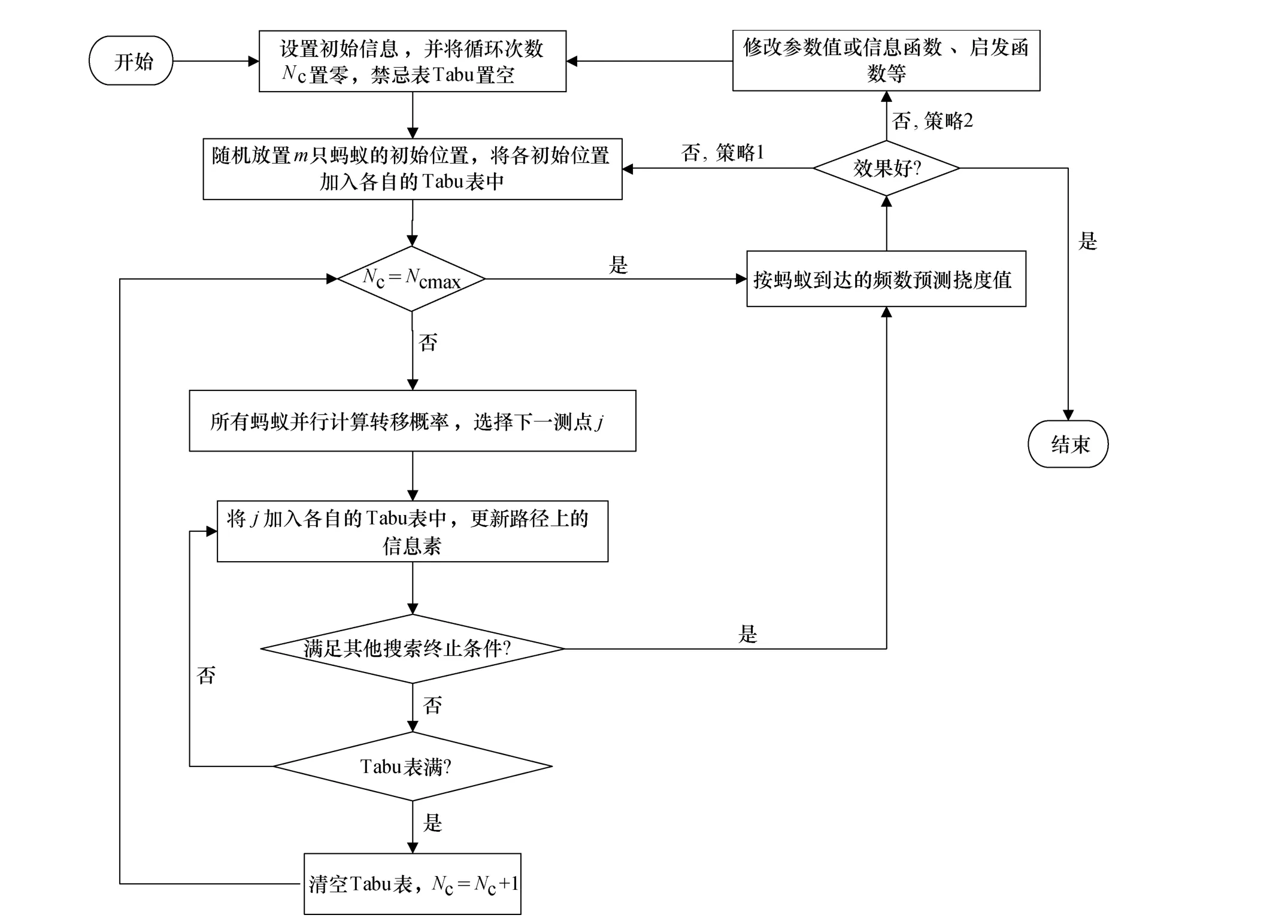
图2 基于蚁群算法的大跨径预应力混凝土桥梁挠度预测流程图
3 基于蚁群优化算法的大跨径预应力混凝土桥梁挠度预测实例
某长江大桥全长2 172 m,主跨为90+3×165+90 m预应力混凝土变截面连续箱梁,桥面宽32.0 m,是一条跨江要道.从2001年大桥通车运营前夕开始定期对桥梁挠度进行监测,上、下游幅分别对称布设了57个挠度监测点,采用精密几何水准测量方法按国家二等水准要求测量.前期每3个月监测一次,3年后每6个月监测一次,截至2012年4月共监测了24期.根据上述算法,编制基于VB的预测程序对桥面挠度进行预测.经反复试验,最终确定模型各参数值分别为 m=40,Q=4 000,α =3,β=4,ρ=0.35 时,算法的总体性能较为平衡.为了验证模型的适用性,对沉降槽的形成和发展2个阶段分别进行预测.在沉降槽形成阶段用2002年3月和2002年6月的监测资料预测2002年9月的挠度变形,在沉降槽发展阶段用2011年4月和2011年10月的监测资料预测2012年4月的挠度变形.图1所示跨中部分18个测点的预测结果见表1(其中绝对偏差=预测值-实测值,相对偏差=绝对偏差的绝对值/实测值).

表1 下游幅跨中部分挠度预测结果 mm
由表1可以看出,在沉降槽初始形成阶段,模型计算得到的2002年9月预测值与实测值非常接近,多个测点的绝对预测偏差近似为0 mm,绝对偏差最大值为-1.9 mm,平均值仅为0.49 mm;相对偏差在0.0% ~18.8%之间,平均为5.7%.在沉降槽进一步发展阶段,模型计算得到的2012年4月预测结果的绝对偏差最小为0.2 mm,最大为4.5 mm,平均值为1.91 mm;其相对偏差在1.6% ~26.1%之间,平均为9.4%.以上2个不同阶段的预测结果表明,该模型具有良好的适用性,且预测精度较高.
为清楚地反映桥梁挠度预测值和实测值间的差异,将预测值相对于实测值的绝对偏差放大10倍后绘制了比较曲线图(如图3所示).由图3可见,实际挠度变形与预测变形趋势较为一致,说明该桥在相应监测期内的挠度变形均符合其变形规律,无异常状况,表明其结构状态良好.同时可以看到,2012年4月沉降槽D23~D28处实测挠度值略大于预测挠度值,说明此处的挠度变形尚在微弱地发展;而在沉降槽 D31~D36处,D31~D34测点的实测挠度值小于预测挠度值,表明该部分挠度变形渐趋稳定,但在D35~D36两测点处却出现了相反的情况.因此可推断,本桥跨中部分的这2个沉降槽挠度变形均未完全收敛,仍需进一步监测.
需要指出的是,除跨中部分外,对南边跨和北边跨的挠度预测结果中,各测点绝对偏差均在±3.0 mm以内,进一步表明了该模型具有较强的适用性和可靠性.另外需要说明的是,在预测2012年4月的挠度时发现,与式(8)相比,按式(7)定义启发函数所得模型精度稍高,这可能是由于式(8)仅考虑了测点空间的差异性,而式(7)同时考虑了空间特性和时间特性,能够较为全面地反映桥梁挠度发展变化的时空效应.

图3 预测值与实测值比较曲线图(绝对偏差放大10倍后)
4 结语
基于TSP蚁群算法构建了大跨度预应力混凝土桥梁挠度变形预测模型,对2个不同阶段的挠度变形预测结果表明,该模型预测精度较高,具有良好的适用性和可靠性.此外,该模型简单、有效,需要的实测数据较少,且易于编程实现,为大跨度预应力混凝土桥梁挠度预测开辟了一条新的途径.同时,该模型在信息函数、启发函数的定义、信息素更新策略的制定等方面尚存在一些问题,比如形式较为单一,不能反映测点之间的关联性等,因此尚有较大的发展空间.
[1]侯世栋.大跨度预应力混凝土梁桥挠度控制研究[D].合肥:合肥工业大学市政工程系,2008.
[2]Hosseini M,Abbas H.Neural network approach for prediction of deflection of clamped beams struck by a mass[J].Thin-Walled Structures,2012(60):222-228.
[3]Chung W,Kim S,Kim N,et al.Deflection estimation of a full scale prestressed concrete girder using longgauge fiber optic sensors[J].Construction and Building Materials,2008,22(3):394-401.
[4]沈月千,黄腾,陈喜凤,等.逐步回归分析在桥梁挠度变形预测中的应用[J].工程勘察,2012(7):79-83.
Shen Yueqian,Huang Teng,Chen Xifeng,et al.The applications of stepwise regression analysis for prediction of bridge deflection[J].Geotechnical Investigation and Surveying,2012(7):79-83.(in Chinese)
[5]Robertson I N.Prediction of vertical deflections for a long-span prestressed concrete bridge structure[J].Engineering Structures,2005,27(12):1820-1827.
[6]Dorigo M,Blum C.Ant colony optimization theory:a survey[J].Theoretical Computer Science,2005,344(2/3):243-278.
[7]Yin P Y,Wang J Y.Ant colony optimization for the nonlinear resource allocation problem [J].Applied Mathematics and Computation,2006,174(2):1438-1453.
[8]Seçkiner S U,Eroĝlu Y,Emrullah M,et al.Ant colony optimization for continuous functions by using novel pheromone updating[J].Applied Mathematics and Computation,2013,219(9):4163-4175.
[9]Ilie S,BǎdicǎC.Multi-agent approach to distributed ant colony optimization[J].Science of Computer Programming,2013,78(6):762-774.
[10]张频婕.蚁群优化算法及其应用研究[D].长沙:中南大学控制科学与工程系,2010.
[11]段海滨.蚁群算法原理及其应用[M].北京:科学技术出版社,2005.
Deflection prediction of long span pre-stressed concrete beam bridge based on ant colony optimization algorithm
Huang Teng1Chen Xifeng1Liu Ling2
(1School of Earth Sciences and Engineering,Hohai University,Nanjing 210098,China)
(2Zhejiang Electric Power Design Institute,Hangzhou 310012,China)
Abstract:In order to solve the problem of inaccurate deflection deformation in the prediction of the long span pre-stressed concrete beam bridge,the ant colony optimization algorithm,which is suitable for complex,uncertain,and nonlinear problems,is proposed.In the algorithm,the information function,which reflects the overall experience of the ant colony,and the heuristic function,which reflects the individual experience of each ant,are used to calculate the transition probability,on which the path selection is based.Then the ant releases a certain concentration of pheromone on the merits of the selected path so as to increase the cumulative experience of the overall ant colony,so a positive feedback and autocatalytic mechanism of the path selection mechanism is formed.The ant colony optimization model of deflection prediction is constructed on the basis of the algorithm and the actual deflection of a long span pre-stressed concrete beam bridge,in which the amount of deflection is considered as the basis of selecting path and releasing pheromone.This model is constructed through the reasonable determination of the information function,the heuristic function,the pheromone updating strategy,and the ant-searching and ant-predicting mechanism.Tested by the deflection prediction from two different stages of settling tank in the mid-span of the bridge,the model shows a high prediction accuracy and a strong applicability,which blazes a new way for analogous bridge deflection prediction.
Key words:ant colony optimization;deflection prediction;long span pre-stressed concrete beam bridge;path selection;information function;heuristic function
中图分类号:TV698.1
A
1001-0505(2013)S2-0235-06
doi:10.3969/j.issn.1001-0505.2013.S2.004
收稿日期:2013-08-20.
黄腾(1957—),男,研究员,博士生导师,njht0911@163.com.
基金项目:江苏省测绘科研资助项目(JSCHKY201301).
引文格式:黄腾,陈喜凤,刘岭.基于蚁群优化算法的大跨度预应力混凝土桥梁挠度预测[J].东南大学学报:自然科学版,2013,43(S2):235-240.[doi:10.3969/j.issn.1001-0505.2013.S2.004]

