基于混合核的支持向量机数字预失真算法﹡
宋 勇, 胡 波, 李在清
(①上海贝尔股份有限公司,上海 201206;②复旦大学电子工程系,上海 200433)
0 引言
随着现代通信系统对频谱资源的需求日益增加,频率效率更高的非恒包络调制方式逐渐取代了原有的恒包络调制方式。但是非恒包络调制方式受功率放大器的非线性效应的影响较大,会产生带内的失真和带外的谱扩散,从而降低频谱效率。因此提高功率放大器的线性度已经成为无线通信系统的一个很有挑战性的问题。
预失真技术是目前应用最广的线性化技术,以它的高效、稳定、自适应等优势成为了目前的研究热点[1-2]。目前使用较多的数字预失真算法采用基于维纳滤波的线性滤波器为基础的多项式模型,主要包括LMS、RLS、KF等算法[3]。支持向量机(SVM,Support Vector Machine)是在Vapnik等人建立的统计学习理论基础上所发展起来的一种新的机器学习算法[4],在处理非线性变换方面具有良好性能,已经被广泛应用到模式识别和回归分析等问题中[5]。
核函数的选择是支持向量机中非常重要的一个环节。文中主要针对功率放大器的非线性特征,相应结合了两种核函数的优点,构造了新型的混合核函数,并运用于数字预失真器中,取得了更好的性能。
1 系统模型
图 1中为采用间接学习法的预失真算法结构图。xk为输入信号,它经过预失真器后生成信号 uk,再通过功率放大器后,就获得输出信号 yk。理想情况下 yk是 xk的一个延迟并放大后的版本(记为,文中设G=1。在每次数据流的循环中,SVM算法利用功率放大器的输入 uk和输出 yk,更新一次预失真函数f并用于下一数据流的预失真器中。
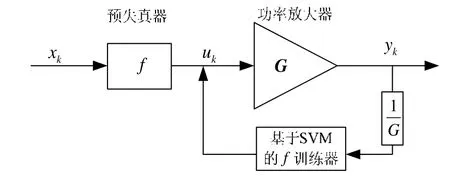
图1 基于间接学习的预失真算法结构
2 基于SVM的预失真器
2.1 基于支持向量机的预失真器模型
支持向量机是一种基于结构风险最小化的统计学习方式[6],它可以最终归结为一个标准二次规划问题,具有全局最优的特性。
在图1的预失真算法结构图中,预失真函数形式如式(2),其中及b相当于未知的预失真系数,记忆深度为M。利用图1中的模型进行f的学习。训练开始时,SVM预失真器是直通的,因此以为输出信号,通过SVM对f进行训练。训练过程可归结为如下的带约束QP问题:为输入信号
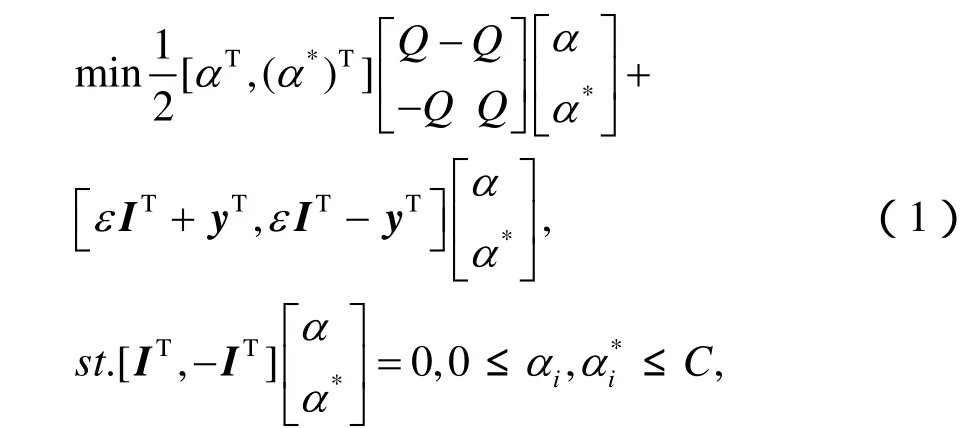
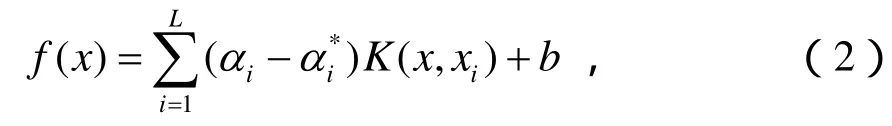
式中,b按下列方式计算:选择位于开区间(0,)C中的jα或,
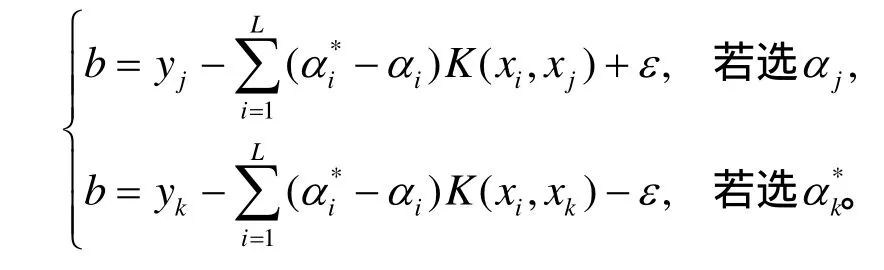
2.2 混合核函数
每种核函数有它们各自的特点,对SVM的回归算法有着不同的影响。SVM的核函数分为全局核函数与局部核函数两类。核函数的性能由学习能力和泛化能力共同决定。
SVM中常用的一个全局核函数是多项式核函数:
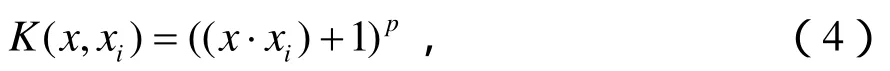
式中,pN∈,多项式核具有较好泛化能力,相距较远的数据也能影响核函数的数值。
傅立叶核是文中主要用到的一种局部核函数:
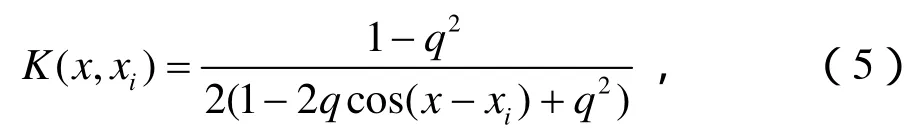
式中,q是满足01q<<的常数。对傅立叶核仅测试点附近的数据点对其有影响,有较好的学习能力,但泛化能力较差。
因此,为了建立一个既有较好学习能力又有较好泛化能力的学习模型,可以充分利用以上两类核函数的各自优点,将其进行组合,因此文中提出了如下的新型混合核函数:
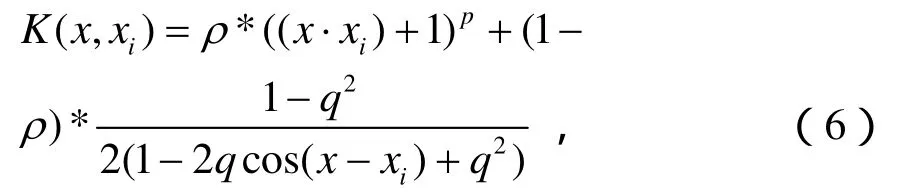
式中,01ρ<<。ρ取值0和1时,混合核函数退化为傅立叶核函数和多项式核函数,其余取值下的核函数,其全局性和局部性均介于傅立叶核函数和多项式核函数之间。
3 仿真与分析
为了验证文中预失真算法的有效性,利用Matlab进行了仿真验证。仿真的输入信号采用带宽为20M的4载波WCDMA信号,采样率为122.88 MHz。
预失真器采用式(2)的模型,样本数L=200,式(1)中结构风险的参数C、ε和式(6)中混合核函数的参数p、q、ρ均由交叉验证法获得最优值,此处分别取值为C=1.58,ε=1e-5,p=3,q=0.67,ρ=0.999。
功率放大器采用Wiener模型,其线性动态子系统的记忆长度为2:
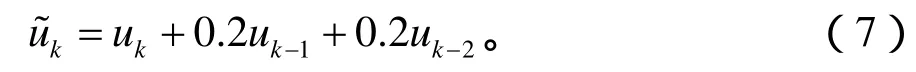
无记忆非线性子系统的阶数为5:
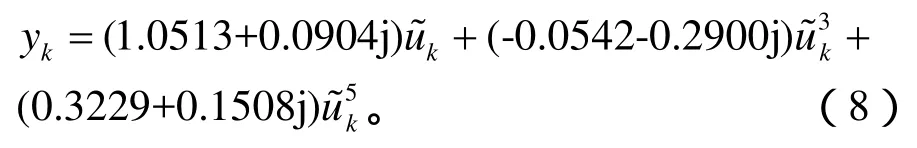
文中的混合核函数中局部核函数是取用的傅立叶核函数,而径向基核函数也是较常用的局部核函数[7],为了验证提出的算法的性能,将文中的混合核函数(P-F-SVM,Polynomial-Fourier SVM)算法与多项式-径向基混合核函数(P-R-SVM,Polynomial-RBF SVM)算法以及傅立叶核函数(F-SVM,Fourier SVM)算法的性能进行了比较。上述核函数中的变量p,q,ρ都已通过交叉验证法取得最优值。
基于LMS的DPD算法是一种广为研究的DPD算法[8]。为了衡量文中提出的DPD算法的性能,与其进行了性能比较。其中基于LMS的DPD算法采用的输入数据长度为10 000,迭代步长0.1μ=,并取0.5ε=。
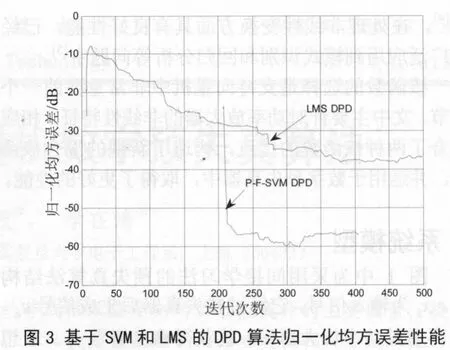
图2给出了基于SVM的几种DPD算法和基于LMS的DPD算法的预失真前后的功率谱密度曲线。从图2中可以看出文中提出的P-F-SVM DPD算法的性能是最优的,优于P-R-SVM DPD和F-SVM DPD两种基于SVM的算法的曲线,也优于基于LMS 的DPD算法曲线,对功率放大器的非线性失真以及记忆失真进行了较好的校正。
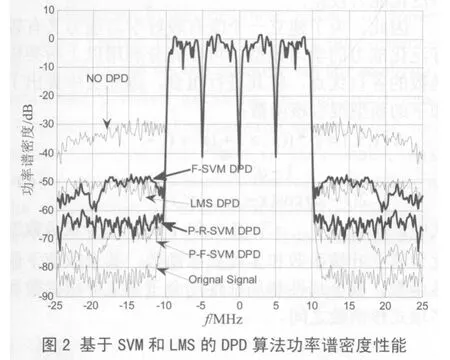
图3中比较了文中提出的基于SVM的算法与基于 LMS的 DPD算法的归一化均方误差(NMSE,Normalized Mean Square Error)收敛曲线,其中图3中的迭代曲线里,P-F-SVM DPD算法的曲线从200以后开始计算,因为它前面的200个点用来生产样本点。从图3中可以看出,P-F-SVM DPD算法的收敛速度比基于 LMS的DPD算法快,而且在迭代收敛后,P-F-SVM DPD算法的平均NMSE性能要比基于LMS的DPD算法高18 dB。
4 结语
文中介绍了SVM算法进行非线性回归的原理,提出了一种基于SVM的DPD算法。通过构造基于傅立叶核函数和多项式核函数的混合核函数,得到了既有较好学习能力又有较好泛化能力的模型。在文中仿真条件下,性能优于基于其它核函数的SVM DPD算法,且与基于LMS的DPD算法相比,文中算法的功率谱密度性能提高了12 dB,NMSE性能提高了18 dB,改善了算法性能,从而提高了功率放大器的线性度。
[1] 陈斌,任国春,龚玉萍.基于多项式与查找表的预失真技术研究[J].信息安全与通信保密, 2011(03):44-46.
[2] 王飞俊,金明录,孙鹏.一种数字预失真器的实现方法[J].通信技术,2011,44(01):154-156.
[3] 张志刚,林其伟,韩霜,等.OFDM系统自适应数字预失真研究[J].通信技术,2011,44(04):50-52.
[4] VAPNIK V.An Overview of Statistical Learning Theory[J].IEEE Transactions on Neural Network,1999,10(05):988-999.
[5] ADANKON M M,CHERIET M,BIEM A.Semisupervised Learning Using Bayesian Interpretation:Application to LS-SVM[J].IEEE Transactions on Neural Networks,2011,22(04):513-524.
[6] CRISTIANINI N,SHAWE-TAYLOR J.An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods[M].Cambridge:Cambridge University Press, 2000: 47-98.
[7] ZHAO Z D,LOU Y Y,NI J H.RBF-SVM and Its Application on Reliability Evaluation of Electric Power System Communication Network[C].International Conference on Machine Learning and Cybernetics, Baoding: IEEE,2009(02):1188-1193.
[8] LI B,GE J,AI B.Robust Power Amplifier Predistorter by Using Memory Polynomials[J].Journal of Systems Engineering and Electronics,2009,20(04):700-705.

