基于移动载荷法的单主梁门式起重机结构的缺陷识别*

赵 俊，钟舜聪，杨晓翔*，郭金泉，龚凌诸

(1.福州大学机械工程及自动化学院，福建福州，350108;2.福建省特种设备检验研究院，福建福州，350001)

0 引 言

起重机正朝着自动化、智能化、核心技术化的方向发展［1-2］，门式起重机作为其中一员，凭借场地利用率高、作业范围大、适应面广、通用性强等特点，在工厂、港口、造船厂、电站等处得到了广泛应用。

随着有限元技术的蓬勃发展，利用有限元分析软件对大型工程结构的数值模拟已成为一种比较流行的方法［3］。胡留现等［4］对小型门式起重机进行了模态分析的数值模拟，发现小型门式起重机结构为一低频振动系统，快速起升和突然卸载时的冲击容易引起结构共振;朱从兵［5］借助有限元分析软件对轻型港口起重机进行了模态分析、谐响应分析、瞬态动力学分析等结构动态响应研究，对起重机优化设计具有指导意义。

近年来，国内外学者对结构缺陷检测方面的研究也产生了浓厚兴趣。龚凌诸等［6］采用自然风的随机激励对港口起重机进行了工作振动模态分析，为基于模态的结构状态监测和裂纹诊断提供了一种有效方法。仲伟秋等［7］和杨永刚等［8］都对振动检测技术在桥梁上的应用提出了自己的方法与见解。Shuncong Zhong等［9］运用附加质量检测法，对杆状结构进行缺陷检测，通过研究发现，附加质量在杆状结构上的移动，能够放大缺陷对杆状结构动态特性的影响效果，从而探测缺陷的所在位置。这种方法具有效率高、鲁棒性好、精度高等优点。Qindan Huang等［10］结合修正的贝叶斯模型和一种基于振动的缺陷检测技术，利用指定结构的动态特性，提出了一种对潜在不确定因素引起的缺陷进行无损检测的方法。

本研究提出的移动载荷法通过用质量单元模拟重物在门式起重机上的移动过程对结构动态特性进行研究，从而得出缺陷所在位置，对推动无损检测的发展起到关键作用。

1 基于移动载荷法的单主梁门式起重机的结构缺陷识别方法

在以往的研究中，有学者研究发现［11］，当缺陷的比例达到50%时，利用有限元技术对模型进行模态分析，有缺陷模型的第一阶弯曲振型相对无缺陷模型来说，其固有频率将会有5%的变化，也就是说，当缺陷深度占整个结构的50%以上时，才能用结构本身的固有频率变化检测出来。所以在缺陷尺寸相对较小的情况下，这是一项非常困难的工作。本研究提出了一种移动载荷法，通过在门式起重机上添加质量单元的方法，模拟重物由主梁一端移动到另一端的过程，以此放大缺陷对结构动态特性产生的影响，达到识别缺陷所在位置的目的。移动载荷法原理示意图如图1所示。

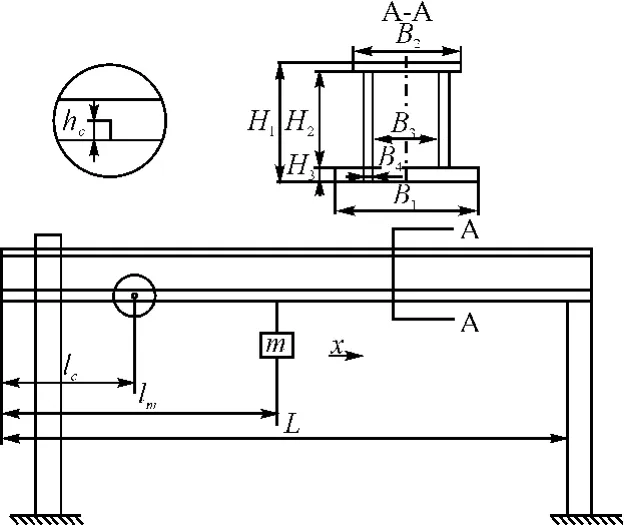
图1 移动载荷法原理示意图

以研究对象单主梁门式起重机为例，尺寸如图1所示，重物由主梁的一端向另外一端缓慢移动。

随着载荷在主梁上的移动，整个结构的固有频率会发生相应地变化，当载荷移动到缺陷所在位置附近，对于整个结构来说，其刚度的变化相对其他远离缺陷的位置要明显得多，并且在缺陷深度增加的情况下，结构刚度变化的程度也会随着增加(相对于无缺陷的刚度)。因此，利用移动载荷法，就能够推断出缺陷所在位置。

2 单主梁门式起重机有限元建模及分析

本研究的研究对象是福建省特种设备检验研究院起重机械健康监测实验室的一台型号为MH0.5-3.5的单主梁门式起重机，其最大起升高度为1.5 m，额定起重载荷为500 kg，跨度为3.5 m，工作级别为A5，主起升速度分为快慢两档:8 m/min和2 m/min，葫芦运行速度分为快慢两档:12 m/min和3 m/min，大车运行速度分为快慢两档:20 m/min和5 m/min，材质为Q235-B，弹性模量为2.1×105MPa，密度为7.85×103kg/m3。该单主梁门式起重机的实物如图2所示。

图2 MH0.5-3.5单梁门式起重机实物图

建模主要以该起重机的金属结构作为研究重点，所以本研究对电气设施和大车运行机构作了适当简化，电动葫芦和载荷用质量点来代替。

2.1 三维模型的建立

本研究利用三维建模软件UG，根据提供的单主梁门式起重机图纸，进行1∶1建模，三维模型如图3所示。

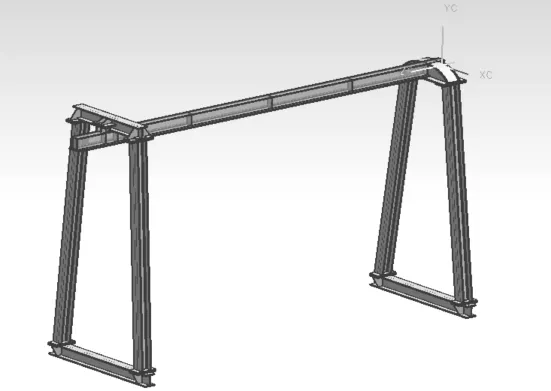
图3 MH0.5-3.5单梁门式起重机三维模型

2.2 建立有限元模型与网格划分

将在UG中建立好的三维模型用IGS格式导入前处理软件Ansa中，可进行有限元模型的形成与网格划分，本研究共得到560 861个节点，387 221个Solid185单元。

2.3 有限元模态分析

在Ansa中建立好有限元模型之后，本研究用cbd格式导入有限元分析软件中进行模态分析。将小车在主梁上运动的有效长度平均分为32点、31段(首尾各有1点)，利用在32个位置添加质量单元MASS21的方式，模拟小车和载荷共100 kg在主梁上运动时所处的不同位置。将底部与大车机构连接的地方设置为全约束(Ux、Uy、Uz、ROTx、ROTy、ROTz都为 0)。本研究在距离悬臂端1 130 mm(小车运动到23号与24号位置序列之间处)的主梁双工字钢下表面处，设置了长120 mm，宽2 mm，深度分别为2 mm、4 mm、6 mm 的规则缺陷(总厚度为8 mm)，分成0%缺陷(无缺陷)、25%缺陷、50%缺陷、75%缺陷共4组有限元模型。50%缺陷网格放大图如图4所示。

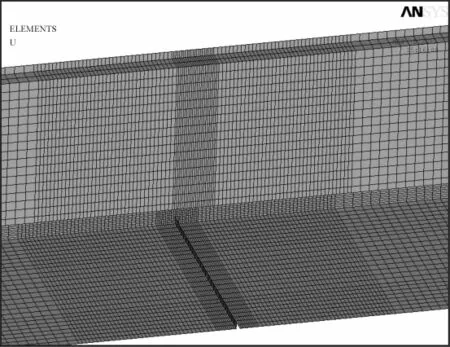
图4 50%缺陷网格放大图

本研究用Block Lanczos法对上述4个模型进行模态分析，在10阶扩展模态中，选出了2个典型的振型，并分别得到了4组模型的2个典型振型的振型图及固有频率曲线。第2振型图如图5所示。

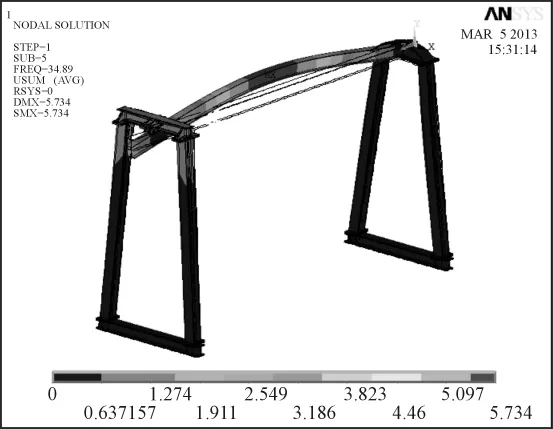
图5 第2振型图

两个典型振型对应的用移动载荷法得到的含有不同缺陷模型的固有频率曲线图如图6所示。

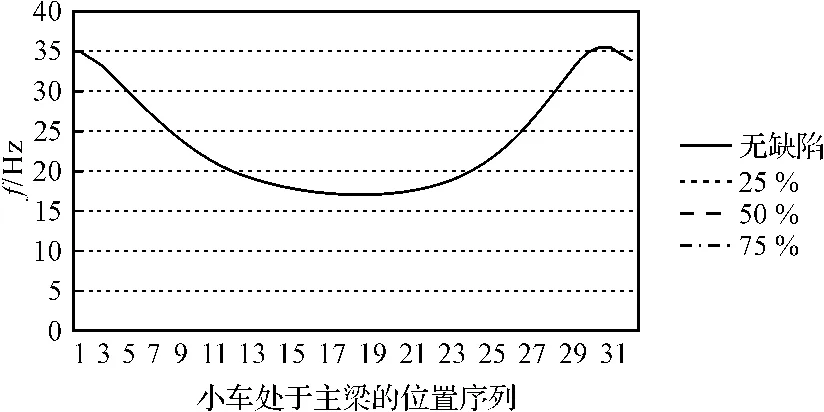
图6 第2振型固有频率曲线图

3 缺陷识别方法及结果讨论

从图6中很难看出4组模型在同样移动载荷情况下的差别。本研究用固有频率值求差的方法，以无缺陷固有频率曲线作为基准，将25%、50%、75%这3组模型得到的固有频率曲线分别与无缺陷模型的固有频率曲线求差，得到的第2振型固有频率差值曲线如图7所示。

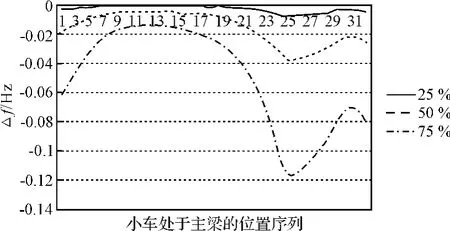
图7 第2振型固有频率差值曲线

从图7可以看出，当质量单元移动到23号与25号位置之间时，固有频率差值有明显的变化，这与之前设定的缺陷位置相符合。对同一振型来说，影响固有频率差值的因素有两个:①缺陷尺寸的大小;②质量单元离开缺陷所在位置的距离。缺陷的尺寸越大，质量单元越接近缺陷所在位置，那么，有缺陷的固有频率值与无缺陷的固有频率值之间的差值就越大，进而说明整个结构的刚度降低越明显。所以，通过移动载荷法可以定性地判断出起重机主梁上缺陷所在的位置，并且在实际的起重机结构无损检测过程中，也可以运用该方法进行缺陷定位。

4 结束语

本研究利用移动载荷法，建立了型号为MH0.5-3.5的单主梁门式起重机的三维模型和有限元模型，并且对4组不同缺陷的模型进行了小车和载重共100 kg

在主梁上运动过程的模拟，提取了两个典型振型的固有频率曲线。笔者对模拟结果进行了固有频率值求差处理，并得出“质量单元在起重机主梁上的移动改变了结构固有频率”的结论。当尺寸的缺陷越大，质量单元越靠近缺陷所在位置，则有缺陷结构的固有频率值与无缺陷结构的固有频率值之间的差就越大，进而达到缺陷定位的目的，该结果为起重机无损检测提供了重要依据。

［1］刘永峰，田洪森.国内外工程起重机发展状况研究［J］.施工技术，2008，37(s2):476-477.

［2］王小明，卢志强.国内外大型起重机的研究现状及发展趋势［J］.机电产品开发与创新，2009，22(2):6-10.

［3］周俊坚，王黎斌，杨 勇.基于ANSYS的一种造船门机金属结构的有限元分析［J］.机械，2012，39(11):49-53.

［4］胡留现，李一帆，王慧萍.小型门式起重机静力学及模态分析数值模拟的研究［J］.矿山机械，2010，38(15):72-75.

［5］朱从军.基于有限元法的轻型港口起重机结构动态分析［J］.中国工程机械学报，2008，6(3):333-339.

［6］龚凌诸，杨晓翔，钟舜聪，等.基于环境激励的港口起重机工作模态分析［J］.机电工程，2011，28(4):422-424.

［7］仲伟秋，孙 国，杨学军，等.桥梁损伤的一种振动检测方法［J］.辽宁工程技术大学学报，2005，24(5):698-699.

［8］杨永刚，罗 韧.有关桥梁振动检测技术的讨论［J］.低温建筑技术，2008，30(4):91-92.

［9］ZHONG Shun-cong，OYADIJI S O，DING Kang.Responseonly method for damage detection ofbeam-like structures using high accu-racy frequencies［J］.Journal of Sound and Vibration，2008，311(3-5):1075-1099.

［10］HUANG Qin-dan，GARDONI P，HURLEBAUS S.A probabilisticdamage detection approach using vibr-ation-based non destructive testing［J］.Structural Safety，2012(38):11-21.

［11］SALAWU O S.Detection of structuraldamage through changes in frequencie-s:a review［J］.Engineering Structures，1997，19(3):718-723.