电液系统中新型反步自适应控制器设计*
袁朝辉,袁 鸣
(西北工业大学自动化学院,陕西西安710072)
0 引 言
反步设计方法是交叉选择Lyapunov函数与反馈控制的递归过程,它将整个系统的设计问题分解为一系列低阶(甚至是标量)子系统的设计问题。利用低阶子系统或标量子系统存在的额外自由度,反步设计方法能在与其他方法相比更宽松的条件下求解稳定控制、跟踪控制和鲁棒控制问题[1]。由于反步法递推系统的设计步骤,不仅可以处理非匹配不确定性,还可以处理带有未知参数的非线性系统,反步法在不确定非线性系统控制设计领域引起了广泛关注[2-7]。基于反步法的各种控制算法为一大类非线性系统提供了系统的跟踪、镇定控制策略设计框架。尤其当干扰和不确定性不满足匹配条件时,自适应反步设计方法已经显示出它的优越性。但反步设计方法也存在着明显的缺陷:在递推设计过程中需要对虚拟控制进行求导,虽然这在理论上不存在任何问题,但却可能导致项数的膨胀最终使得每一步都很复杂,控制器的复杂程度随着系统阶数的增加而急剧增加[8-10]。近年来,基于反步设计思想,部分学者提出了多滑模控制方法,该方法在解决反步法计算膨胀问题上具有一定的效果,但为了克服不确定性必须增大各滑模增益,且各滑模的趋近轨迹无法得到保证。
本研究控制方法采用CMAC神经网络在线估计系统的不确定性和虚拟控制导数项,有效解决在对虚拟控制进行求导时产生的计算膨胀问题;同时,在控制输入前加入低通滤波器,使控制量连续化,消除滑模控制可能产生的抖振问题,使控制效果达到预期效果。
1 反步法原理
考虑如下类型的单输入、单输出非匹配不确定非线性系统:

首先,定义虚拟反馈误差变量为:

式中:yd—期望系统输出;z—n维虚拟误差状态变量)—待定虚拟反馈。
反步法对每一步构造一个Lyapunov函数,使每一步的虚拟误差状态分量zi渐近收敛于零,最终系统输出y=x1,渐近收敛于期望系统输出yd。
反步法实际上是一种由前向后递推的设计方法,通过逐步迭代设计Lypaunov函数,最终实现系统的镇定或跟踪。反步法比较适合在线控制,能够达到减少在线计算时间的目的。反步法中引入的虚拟控制本质上是一种静态补偿思想,前一个子系统必须通过其后子系统的虚拟控制才能达到镇定目的,因此该方法要求系统结构必须是与式(1)类似的严参数反馈系统,或可经过变换化为这种类型的非线性系统。
2 电液力伺服系统的自适应反步控制
2.1 电液力伺服系统非线性数学模型
本节针对电液力伺服系统非线性数学模型,将反步设计算法与CMAC神经网络相结合,设计了鲁棒自适应输出跟踪控制器,有效地解决了运动扰动和系统参数不确定性问题,提高了载荷谱跟踪精度。
假设期望输出力轨迹为Fd,则由于F=Kt(xtxy),可知期望液压缸位移输出为xtd=Fd/Kt+xy,可通过设计控制律使得液压缸输出位移渐近跟踪期望输出位移,从而达到渐近跟踪期望输出力的目的。

其中:

式中:Cv—滑阀节流窗口的节流系数;w—伺服阀的面积梯度,m;ρ—油液密度;sgn(·)—符号函数;pf—负载压降;xt—加载液压缸位移;xy—位置系统干扰位移;mt—负载等效质量;Kt—负载弹性刚度;Bt—粘性阻尼系数;At—加载液压缸截面积;Ey—油液弹性模量;Vt—加载液压缸等效容积;Csl—总泄漏系数;F—加载力。
2.2 自适应反步控制器设计
首先,设计CMAC神经网络逼近不确定性:

式中:wi—理想权值向量—权向量的估计—误差权向量,εi—逼近误差。
定义虚拟反馈误差:

当i=1时,x1d为系统期望输出轨迹,x1d=xtd=Fd/Kt+xy;当i≠1时,xid为系统虚拟控制量,xi为系统实际状态变量,i=1,2,3。
2.2.1 虚拟控制输入量

定义Lyapunov函数为:

对其求导可得:

其中:

并取:

有下式:

设虚拟期望连续控制输入为ud,定义实际控制输入与期望输入之间的误差为z4=u-ud。
定义Lyapunov函数为:

对其求导可得:

其中:

并取虚拟控制输入ud为:

2.2.2 低通滤波器设计

式中:τ—低通滤波器时间常数,v—低通滤波器输入。且:

其中:
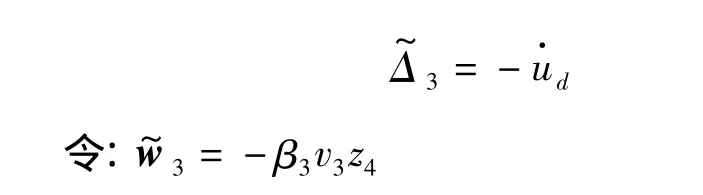
并取低通滤波器输入v为:

其中:

3 仿真研究
为研究所提出的算法性能,笔者对其进行了仿真研究。系统仿真工具为Matlab/Simulink环境,仿真步长采用0.001 s固定步长,仿真算法采用四阶龙格-库塔函数。
电液力伺服系统为:

其中:

系统主要参数如表1所示。控制器主要参数为:k1=1 000,k2=16 000,k3=1 500,δ1=0.001,δ2=0.1,δ3=1 000,CMAC权值调整参数 β 为0.2,泛化参数 C为100,量化等级为10 000,低通滤波器参数 τ=0.002。仿真中,考虑电液伺服阀输入电流饱和,其上、下限为±40 m。

表1 电液力伺服系统主要参数
加载指令为0、舵机运动指令为60 sin(10πt)mm时产生的多余力仿真结果,如图1所示。
由图1可见,多余力不足50 N,本研究所提控制方法有效地抑制了舵机的运动干扰,且控制输入连续无抖振。为考察该控制方法对输入指令的跟踪性能,笔者对某型舵机进行了气动载荷加载仿真研究,某飞行试验状态下舵机载荷谱跟踪的仿真结果如图2所示。仿真中,舵机位移运动规律为60 sin(10πt)mm,加载力载荷谱为F=F0+FAsin(10πt)N的仿真结果。其中,F0、FA为与飞行状态有关的量,5 500+3 000sin(10πt)N。

图1 多余力仿真结果

图2 气动载荷谱跟踪误差仿真结果
载荷谱跟踪误差如图2所示。由图2中仿真结果可见,本研究所提控制策略具有较高的跟踪精度。为了进一步验证该控制策略的鲁棒性,令参数Csl为额定值的2倍,Bt为额定值的0.5倍,Ey为原来的70%,其仿真结果如图3所示。

图3 有、无CMAC时系统鲁棒性验证
图3(a)中,曲线1为力载荷谱,曲线2为采用本研究控制策略时系统实际响应,曲线3为无CMAC时系统实际响应;图3(b)中,曲线1为无CMAC时系统载荷谱跟踪误差,曲线2为采用本研究控制策略时系统载荷谱跟踪误差。由图3仿真结果可见,无CMAC时参数不确定性使得原控制器对系统的控制效果变差,而有CMAC时自适应鲁棒控制器有效抑制了参数不确定性对系统的影响,具有较高的载荷谱跟踪精度。因此,本研究所提出的自适应反步法采用CMAC神经网络在线学习系统不确定性,能够确保系统在参数摄动情况下仍具有较好的控制性能。
4 结束语
本研究所提出的新型自适应反步控制算法采用CMAC神经网络在线学习系统不确定性以及各阶虚拟控制量的导数信息,从而避免了反步法在系统阶次较高时引起的计算膨胀问题;该控制算法在递推设计的最后一步加入非连续鲁棒项,以克服CMAC神经网络在线学习系统不确定性的残余误差,同时,在控制输入前加入低通滤波器,使得符号函数产生的控制不连续项到达实际执行机构前连续化,能够避免不连续控制输入可能产生的抖振问题。另外,本研究将所提出的控制算法应用于电液力伺服系统,并进行了仿真验证,仿真结果表明本研究所提出的控制算法能够有效抑制系统不确定性,具有较好的指令跟踪性能。
(References):
[1]王占林.液压伺服控制[M].北京:北京航空航天大学出版社,1987.
[2]KHALIL H K.Nonlinear Systems[M].Prentice Hall,1996.
[3]LIN F J,SHIEN P H,CHOU P H.Robust adaptive backstepping motion control of linear ultrasonic motors using fuzzy neural network[J].IEEE Transactions on Fuzzy Systems,2008,16(3):676-692.
[4]FRANCESC P,FAYCAL I,JOSE R.Numerical issues in backstepping control:sensitivity and parameter tuning[J].Journal of the Franklin Institute,2008,345(8):891-905.
[5]HSU C F,LIN C M.Fuzzy-identification based adaptive controller design via backstepping approach[J].Fuzzy Sets and Systems,2005,151(1):43-57.
[6]NURKAN Y,YUKSEL H.Backstepping control of a vehicle with active suspensions[J].Control Engineering Practice,2008,16(12):1457-1467.
[7]OZBAY U,ZERGEROGLU E,SIVRIOGLU S.Adaptive backstepping control of variable speed wind turbines[J].International Journal of Control,2008,18(6):910-919.
[8]HUANG S J,HUANG K S,CHIOU K C.Development and application of a novel radial basis function sliding mode controller[J].Mechatronics,2003,13(4):313-329.
[9]张海鹏.鲁棒滑模反步控制法及其在减摇鳍中的应用[D].哈尔滨:哈尔滨工程大学自动化学院,2004.
[10]吴玉香.滑模控制理论及在移动机械臂中的应用[D].广州:华南理工大学自动化科学与工程学院,2006.

