TC21钛合金电子束焊接件疲劳断口定量反推研究

郑志腾，有移亮，刘新灵，张 峥，路浩天

（1北京航空航天大学 材料科学与工程学院，北京 100191；2北京航空材料研究院，北京 100095；3中航工业 综合技术研究所，北京 100028）

TC21是国内自主研发的高强高韧综合力学性能匹配较好的钛合金之一，可用于飞机的机翼接头结构件、机身与起落架连接框、吊挂发动机接头等部位，以及对强度及耐久性要求高的关键承力部件的制作［1－3］。电子束焊接由于能量密度高、焊缝和热影响区窄、焊接变形小、工艺参数容易精确控制以及真空焊接环境等其他焊接方法难以比拟的优势而广泛应用于航空、航天及工业制造中。在焊接结构中，与疲劳相关的结构失效事故占金属结构失效事故的70%～80%［4］。断口分析是判断失效件失效模式、确定失效机理、找出失效原因的重要手段［5］。对钛合金疲劳断口的定量反推已有所研究。张卫方等［6］对钛合金在实验和工程应用条件下的构件进行断口定量反推，研究疲劳条带间距反推应力在钛合金应用的可行性；王翀等［7］利用Paris公式，分别运用自然对数法和常用对数法对TA15钛合金进行了寿命反推，结果表明，在相同的条件下，应用常用对数和自然对数法计算的扩展寿命十分接近；李仲等［8］对TC4钛合金锻件紧固孔结构细节的原始疲劳质量进行了研究；Manning和Yang［9］对多种钛合金材料的原始疲劳质量分布进行了研究，提出的结构件耐久性设计和分析技术得到了广泛的应用。但关于钛合金电子束焊接件疲劳断口定量反推的研究还鲜见报道。

本工作对TC21钛合金电子束焊接接头的组织和疲劳断口特征进行了分析，并对疲劳断口进行了基于宏观扩展区面积和微观疲劳条带的定量表征，对疲劳应力和焊接结构的原始疲劳质量（当量裂纹长度）进行了反推研究，旨在为钛合金电子束焊接结构在工程上的应用提供依据和参考。

1 实验材料及方法

实验采用TC21钛合金锻制厚板，板材厚度为10mm，其主要成分如表1所示。电子束焊接工艺为加速电压150kV，聚焦电流2100mA，电子束流90mA，焊接速率为300mm／min。

表1 TC21钛合金化学成分（质量分数／% ）Table 1 Chemical composition of TC21（mass fraction／%）

沿垂直于焊缝方向截取焊接板材，取其中间部位作为疲劳试样，将疲劳试样打磨抛光，试样规格如图1所示。在室温条件下，用GZ－100C型疲劳机对TC21电子束焊接接头试样做轴向加载疲劳试验，应力比为R＝－1。在FEI QUNATA 400型扫描电子显微镜下观察疲劳断口。

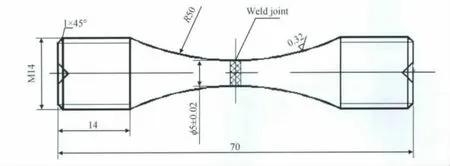
图1 疲劳试样的形状和尺寸Fig.1 Schematic illustration of the fatigue specimens

2 微观组织和疲劳断裂特征

2.1 TC21钛合金电子束焊接接头微观组织

实验用TC21钛合金的金相组织见图2（a），母材的显微组织为魏氏组织形貌，组织中有粗大的原始α晶粒，α相互相交错，呈编织状，α相间为β相。真空电子束焊接接头明显地分为焊缝区、熔合区、热影响区以及未受影响的母材。焊缝组织为粗大的β柱状晶，由焊缝两侧向焊缝中心生长，并在焊缝中心破碎，成为新的形核质点，长大成为细小的β等轴晶。β柱状晶粒内部为快冷形成的细小马氏体针，同一晶粒内的马氏体针平行排列，如图2（b）所示。这是由于电子束焊接过程中冷却速率很大，β相来不及通过原子扩散转变成平衡态的α相，只能发生切变相变，生成针状含过饱和α相稳定元素的马氏体 。

图2 TC21钛合金焊接接头组织 （a）母材组织；（b）焊缝组织Fig.2 Microstructures of TC21joint （a）base metal；（b）welded metal

2.2 TC21钛合金电子束焊接接头的疲劳断裂特征

TC21钛合金焊接接头的疲劳断口一般可分为疲劳源区、疲劳裂纹扩展区、瞬断区三个区域。

（1）疲劳源区：疲劳裂纹一般起源于试样表面（图3（a））或内部缺陷处，其中缺陷主要为气孔缺陷，如图3（b）所示。在有焊接缺陷存在时，钛合金焊接接头的疲劳裂纹基本上都是起源于焊接缺陷，并以缺陷为中心向四周放射状扩展。缺陷处与基体之间弹性模量不匹配造成局部应力集中，以及其他形式的残余应力的相互作用在缺陷周围形成较大的应力集中，在外加载荷的作用下，基体发生滑移，位错缠结在缺陷周围，位错塞积造成更大的应力集中。缺陷处的脆性较大，在外加载荷和较大应力集中作用下，导致缺陷处自身的断裂，从而形成微裂纹［9］。对于钛合金焊接接头，焊接缺陷不可避免，使得疲劳裂纹多从缺陷处萌生。在疲劳裂纹形成的过程中，裂纹不断张开、闭合，形成光滑小刻面，见图4（a）。

图3 疲劳断口源区的SEM像 （a）表面起源；（b）内部气孔起源Fig.3 SEM images of fatigue crack initiation sites （a）surface；（b）internal pore

图4 疲劳断口源区（a）和瞬断区（b）高倍SEM像Fig.4 SEM micrographs of fatigue fracture initiation sites（a）and fracture sites（b）

（2）疲劳裂纹扩展区：疲劳裂纹稳定扩展阶段形成的特征区域称为疲劳扩展区，该区的宏观特征为断面较平坦，与主应力相垂直［10］。疲劳裂纹的稳定扩展按其形成机理与特征的不同又可分为两个阶段：即疲劳裂纹稳定扩展第一阶段与疲劳裂纹稳定扩展第二阶段。疲劳裂纹稳定扩展的第二阶段的显微特征主要是疲劳条带。

（3）瞬断区：瞬断区呈剪切唇形貌，随应力水平的增加高差变大。瞬断区形貌较粗糙，均呈韧窝状，见图4（b）。

3 电子束焊接疲劳断口的定量反推

3.1 断口宏观面积反推疲劳应力

疲劳扩展区的大小可以用疲劳扩展临界裂纹长度ac来表征［12］。疲劳临界裂纹长度ac与最大交变应力σmax密切相关，已知：

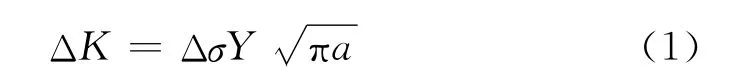
式中：Y是与裂纹有关的形状因子；a是裂纹长度；Δσ是构件承受的应力幅值；ΔK是裂纹尖端的应力强度因子。

当裂纹发生快速扩展时，ΔK＝KIC（1－R），a＝ac，σmax＝Δσ／（1－R），则可按下式求得零件断裂时的最大工作应力σmax。

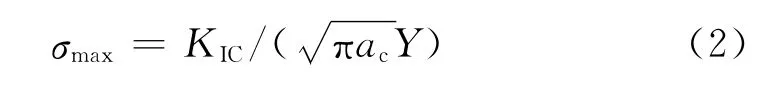
扩展区是疲劳裂纹达到临界尺寸发生快速破断前所形成的区域，在应力水平较低时，可以将扩展区近似成为一圆形区域，则扩展区的面积A与临界裂纹长度ac的关系为A＝π（ac／2）2，代入（2）式可得：

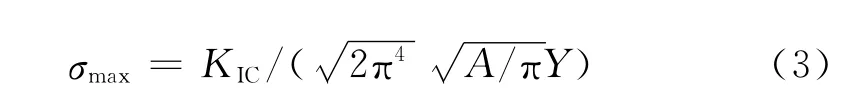
临界应力强度因子KIC是材料抵抗裂纹失稳扩展的能力，是材料本身所具有的一种力学性能指标，因此，在材料断裂韧性一定的情况下，有：

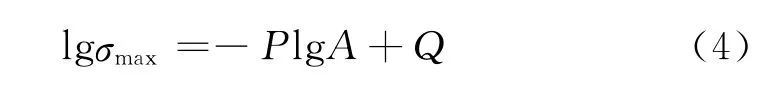
其中P和Q均为常数。式（4）即为断口扩展区宏观面积反推疲劳应力的基础。

用图形处理软件image J测量不同应力下典型疲劳断口的扩展区面积，统计结果如表2所示。图5（a）和图5（b）分别为350MPa和450MPa下焊接接头典型疲劳断口的宏观SEM图。结合图5和表2可以看出：随着应力水平的增加，断口临界裂纹长度ac减小，扩展区的面积A也减小。将得到的应力和面积数据取对数后进行线性拟合，结果如图6所示，即可得到lgσmax和lgA的定量关系：

lgσmax＝－0.9162lgA＋3.6489；相关系数r＝0.9134。

表2 不同应力下疲劳断口扩展区面积统计表Table 2 The area of propagation zone under different stress

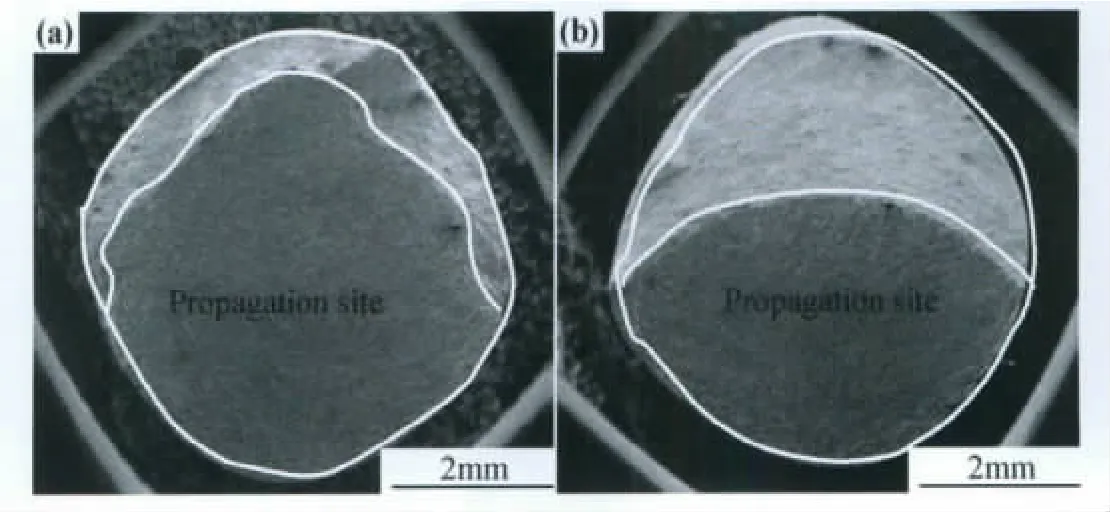
图5 不同应力下疲劳断口宏观SEM图（a）350MPa；（b）450MPaFig.5 SEM images of fatigue fracture under different loads（a）350MPa；（b）450MPa

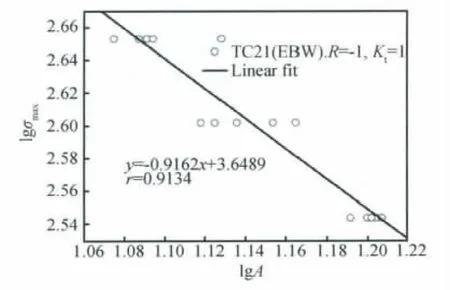
图6 A与σmax对数关系图Fig.6 Logarithmic relationship between Aandσmax

用拟合数据外的断口扩展区面积A对拟合结果进行校核［4］：

（1）350MPa时，测得A＝14.56mm2，反推计算得应力

σmax＝10（－0.9162×lg14.56＋3.6489）＝383.01MPa

误差ε＝［（383.01－350）／350］×100%＝9.43%

（2）400MPa时，测得 A＝12.88mm2，反推计算应力

σmax＝10（－0.9162×lg12.88＋3.6489）＝428.54MPa

误差ε＝［（428.54－400）／400］×100%＝7.14%

（3）450MPa时，测得 A＝11.21mm2，反推计算应力

σmax＝10（－0.9162×lg11.12＋3.648）＝486.69MPa

误差ε＝［（486.69－450）／450］×100%＝8.15%

由计算结果可知，在断裂韧性相同的情况下，可由扩展区面积反推应力，且反推计算所得的应力与实际的疲劳应力的相对误差在10%以内。

3.2 疲劳条带反推原始疲劳质量

3.2.1 疲劳条带的测量

将断口置于扫描电镜下观察，测量不同裂纹长度和对应的疲劳条带间距。从断口源区开始，寻找疲劳条带特征（通常情况下，由于源区的疲劳条带极细，并且可能受到摩擦，因此很难观察到疲劳条带）；找到第一次观察疲劳条带的位置，在一定放大倍数下（能够测量相邻条带的间距）拍照记录；以此类推，测量出距源区不同距离ai处的疲劳条带的间距dai／dN，直到瞬断区为止，共取5个测量点，每个点区域内取三处测量结果的平均值作为该处疲劳条带的宽度值。在满足工程应用的前提下，应遵循的测量原则为：①测量与断口基本在同一平面上的多个并排的疲劳条带，尽量选择数量多、分布均匀、轮廓清晰的条带进行测量；②一般不测量倾斜于断口主裂纹方向的疲劳条带，以防止实测结果偏小；③对于斜面上的疲劳条带，可利用扫描电镜的倾斜功能，将斜面变成平面，再对其上的疲劳条带进行测量；④在同一测量区内疲劳条带宽度变化不大，应测量多个并排的疲劳条带数据，取其平均值作为实测数据以便减小多种因素造成的误差［12，13］。以400MPa 8号试样疲劳断口为例，测得其5处裂纹长度和对应的疲劳条带宽度如表3所示。取点位置以及疲劳条带形貌见图7。

图7 8号试样不同裂纹长度处疲劳条带高倍SEM图Fig.7 SEM micrographs of fatigue striation for different crack length of No.8specimen

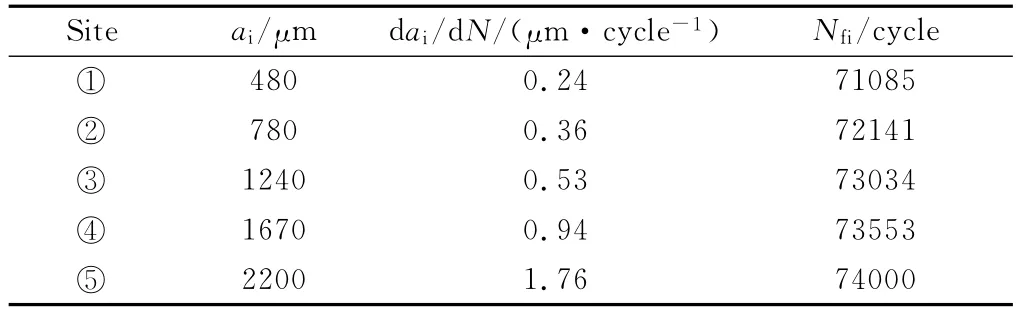
表3 8号试样不同裂纹长度对应的疲劳条带宽度及总寿命Table 3 The width of fatigue striation and final fatigue life for different crack length of No.8specimen

3.2.2 Paris公式反推焊接件的原始疲劳质量

结构件在服役前带有初始裂纹或缺陷，损伤容限设计思想中的初始裂纹，就是指把存在于构件中的初始缺陷群等效的归结为一个非实体的当量裂纹长度，称之为当量初始裂纹a0i，并以此作为表征构件质量的参量，因此也称为当量初始质量。因此，a0i虽是一个假设的裂纹长度，却又综合反映了构件中的材质以及加工制造质量，所以又将a0i称为原始疲劳质量。原始疲劳质量反推的基础是Paris公式：

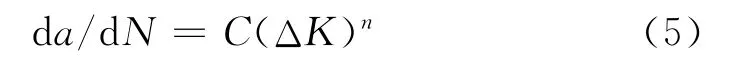
式中C，n是材料常数，与材料的微观组织结构、循环加载的频率、波形、环境、温度和应力比R有关。应力强度因子幅值可表示为ΔK＝，其中A＝yΔσπ1／2＝常数。

将其代入Paris公式得：

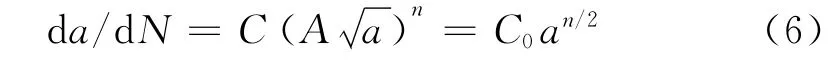
其中，C0＝。令y为裂纹扩展深度a的函数y（a），则有：

令G＝C（Δσ）nπn／2，f（a）＝［y（a）］nan／2，则上式写成：

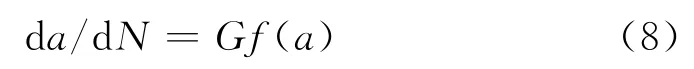
设f（a）＝aB，对上式两边取自然对数有：

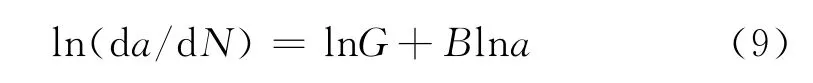
令ln（da／dN）＝Y，lnG＝A，lna＝X，则得到线性方程Y＝A＋BX。通过回归分析可确定式中的A，B两个常数。则原式可以改写成da／dN＝eA·aB（μm／cycle）。对上式进行积分变化后得疲劳载荷循环次数Np的表达式为：

式中，a0为初始裂纹值，a0的值参考美国空军制定的表面裂纹长度约为0.794mm（1／32in）时所对应的裂纹深度，考虑到表面裂纹的半椭圆形貌，深度方向为椭圆轴方向，取a0＝0.3mm为积分下限；ai为裂纹扩展到某一点时的裂纹深度，为积分上限［4］。

用试件的疲劳总寿命Nf减去扩展寿命Np得到萌生寿命Ni，再将每个裂纹长度对应的扩展寿命Npi和萌生寿命Ni加和，得到每个裂纹长度对应的总寿命Nfi，计算后拟合实测曲线，然后将曲线反推至时间为零，即N＝0，曲线与纵坐标的交点即为该构件的a0i。本工作采用指数增长（Exponential Growth）拟合函数［14］进行拟合。

式中：A1是强度；t1是增长幅度；y0即为试件的原始疲劳质量。

对8号试样测得的ai和dai／dN取对数进行拟合，结果如图8所示，得到lna和ln（da／dN）的关系为：

y＝1.2577x－9.3382；相关系数r＝0.9421。

图8 a与da／dN对数关系图Fig.8 Logarithmic relationship between aand da／dN

即A＝－9.3382，B＝1.2577。其疲劳总寿命为74000，计算裂纹扩展到五个测量点时的寿命，结果见表3。然后将计算结果拟合，结果如图9所示，得到a与N的指数增长关系为：

y＝A1e（x／t1）＋321.80；相关系数r＝0.9985。

得到8号试样原始疲劳质量为321.80μm。

R＝－1时TC21钛合金焊接接头的原始疲劳质量拟合结果如表4所示。

图9 N与a指数增长关系图Fig.9 Exponential growth relationship between Nand a

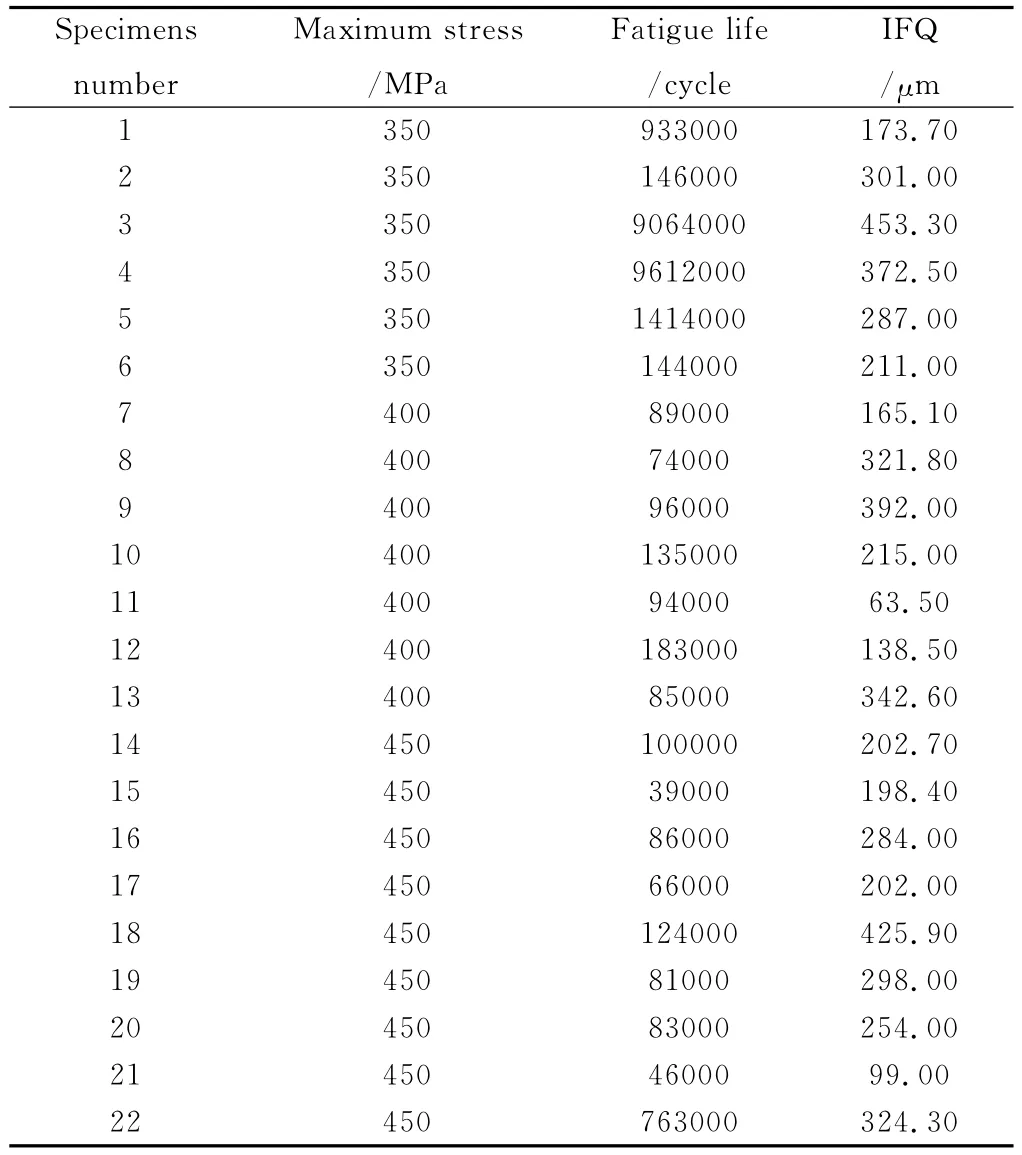
表4 TC21焊接接头原始疲劳质量反推结果统计表（R＝－1，Kt＝1）Table 4 The results of estimated initial fatigue quality（IFQ）for TC21Ti alloy welding joint（R＝－1，Kt＝1）

用Matlab软件对表4中的原始疲劳质量数据进行拟合，结果如图10所示。

图10 原始疲劳质量正态分布图Fig.10 Normal distribution of IFQ

由上述分析结果可知，用当量初始缺陷尺寸分布所表示的原始疲劳质量必须用一个相关的断口形貌测量结果的反推来确定，概率分布是研究原始疲劳质量十分方便的数学工具。

4 结论

（1）在断裂韧性相同的情况下，可由扩展区的面积反推钛合金电子束焊接构件承受的应力，反推计算所得的应力与实际的疲劳应力的相对误差在10%以内。

（2）在测量扩展区不同长度裂纹处疲劳条带宽度值的基础上，可利用Paris公式反推焊接结构的原始疲劳质量，原始疲劳质量呈正态分布且分散度较大。

［1］杨慧丽.TC21钛合金φ350mm棒材显微组织与性能的关系［J］.中国钛业，2001，（3）：19－22.YANG Hui－li.The relationship between microstructure and property ofφ350mm rod like TC21titanium［J］.China Titanium Industry，2001，（3）：19－22.

［2］宋颖刚，高玉魁，陆峰，等.TC21钛合金喷丸强化层微观组织结构及性能变化［J］.航空材料学报，2010，30（2）：40－44.SONG Ying－gang，GAO Yu－kui，LU Feng，et al.Evolution of microstructure and properties of surface layer after shot peening of TC21titanium alloy［J］.Journal of Aeronautical Materials，2010，30（2）：40－44.

［3］姜波，王耀奇，侯红亮，等.氢对TC21合金高温变形行为的影响［J］.材料工程，2011，（5）：70－75.JIANG Bo，WANG Yao－qi，HOU Hong－liang，et al.Effects of hydrogen on hot deformation behavior of TC21alloys［J］.Journal of Materials Engineering2011570－75.

［4］张燚，章文峰，闫海.断口定量分析在评估构件疲劳寿命中的应用［J］.材料工程，2000，（4）：45－48.ZHANG Yi，ZHANG Wen－feng，YAN Hai.Quantitative analysis in evaluating fatigue lives of components［J］.Journal of Materials Engineering，2000，（4）：45－48.

［5］钟群鹏，田永江.失效分析基础知识［M］.北京：机械工业出版社，1990，121.

［6］张卫方，高威，赵爱国，等.钛合金断口反推疲劳应力的实验与工程应用研究［J］.机械强度，2003，（4）：436－437.ZHANG Wei－fang，GAO Wei，ZHAO Ai－guo，et al.Fatigue stress estimation for titanium alloy by fatigue crack striation［J］.Journal of Mechanical Strength，2003，（4）：436－437.

［7］王翀，张峥，刘新灵.TA15钛合金疲劳寿命反推研究［J］.金属热处理，2007，32（增刊1）：437－439.WANG Chong，ZHANG Zheng，LIU Xin－ling.Fatigue life prediction of TA15titanium alloy［J］.Heat Treatmeat of Metals，2007，32（S1）：437－439.

［8］李仲，葛森，陈莉，等.钛合金的原始疲劳质量研究［A］.中国数学力学物理学高新技术交叉研究学会第十二届学术年会论文集［C］.四川峨眉山：2008，242.

［9］MANNING S D，YANG J N.USAF Durability Design Handbook［M］.2nd ed.USA：AFW L－TR－83－3027，1988.

［10］张秉刚，王廷，陈国庆，等.大厚度TC21钛合金电子束焊接试验［J］.焊接学报，2009，30（11）：6－11.ZHANG Bing－gang，WANG Ting，CHEN Guo－qing，et al.TC21titanium alloy electron beam welding test with big thickness plate［J］.Transactions of the China Welding Institution，2009，30（11）：6－11.

［11］蹇海根，姜锋，文康，等.不同应力下7B04铝合金的疲劳断口［J］.中南大学学报：自然科学版，2010，41（1）：137－143.JIAN Hai－gen，JIANG Feng，WEN Kang，et al.Fatigue fracture of 7B04aluminum alloy under different stresses［J］.Journal of Central South University：Science and Technology，2010，41（1）：137－143.

［12］刘新灵，张峥，陶春虎.疲劳断口定量分析［M］.北京：国防工业出版社，2010.47－49.

［13］赵子华，张峥，吴素君，等.金属疲劳断口定量反推研究综述［J］.机械强度，2008，（3）：59－63.ZHAO Zi－hua，ZHANG Zheng，WU Su－jun，et al.Survey of quantitative reverse deduction from fatigue fracture surface of metals［J］.Journal of Mechanical Strength，2008，（3）：59－63.

［14］茆诗松，贺思辉.概率论与统计学［M］.武汉：武汉大学出版社，2010.87－88.