玻璃-金属压封式热管真空太阳集热管封接应力计算与分析

■ 焦青太 魏宝成 殷志强

（1.太阳雨太阳能集团有限公司；2.清华大学电子工程系）

一 引言

玻璃－金属封接式热管真空太阳集热管可作为太阳能中温热利用的核心部件，将玻璃管与金属板用低熔点金属焊料进行压封是可选择的一种封接方式。

压封具有结构简单、部件易加工、对装配的精度要求低等优点。压封封接完成并降温后，由于膨胀系数不同，玻璃管和金属板的收缩量不同，压封件中会产生无法消除的残余应力[1]。将玻璃管中的残余应力称为封接应力。封接应力与真空致密性是封接件中的两个关键问题。这里研究分析封接应力，特别是最危险的玻璃拉应力。

殷志强等人[2]对陶瓷－金属平面封接中的应力进行了分析与计算。本文将对玻璃-金属压封件中的封接应力进行分析与计算。

二 玻璃-金属压封封接应力计算公式

对玻璃－金属压封封接应力进行分析时，所简化为：(1)适用板壳理论；(2)忽略低熔点金属焊料对应力的影响；(3)金属板中应力在弹性限度以内；(4)忽略玻璃管翻边与金属板上小孔。

玻璃－金属压封件实物如图1所示。图2是压封件的简化示意图，其中，tg表示玻璃管的厚度；tm表示金属板的厚度；R表示玻璃管的平均半径。

图1 玻璃-金属压封件

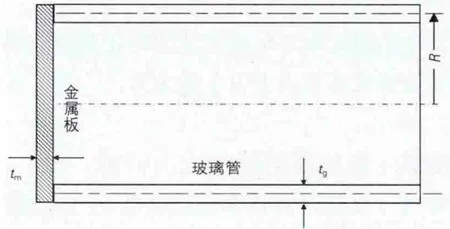
图2 玻璃-金属压封件简化示意图

玻璃管与金属板通过端面相互作用。通常金属板比玻璃管膨胀系数大，因此金属板收缩量大，在玻璃管端面圆周上会产生单位长度的内力P，内力P使玻璃管端面收缩、旋转，同时还有单位长度的力矩M，对P所引起的收缩、旋转起到抵消作用。同时P和M方向相反地作用在金属板端面上。

对完好的玻璃－金属压封件，玻璃管与金属板的位移和转角是连续的，根据位移与转角协调方程可得到[2]：

其中，α为金属板与玻璃管平均线膨胀系数之差，α=αm-αg；T为封接粘着后的温度与室温之差；R为玻璃管的平均半径。

玻璃管和金属板的各种柔性系数为：

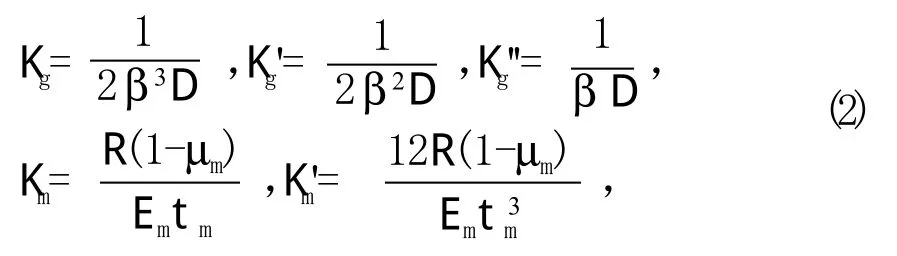
并且：

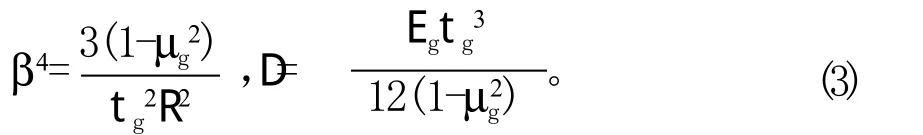
式中，Eg、Em分别为玻璃管、金属板的杨氏模量；µg、µm分别为玻璃管、金属板的泊松比。

在得到端面上的P与M后，可进一步求出玻璃管上的轴向应力σx、周向应力σθ、平均剪应力τxr[2]：

其中，轴向应力σx表达式中的正负号分别表示玻璃管外表面和内表面上的应力。

三 玻璃-金属压封封接应力计算

玻璃－金属压封件的设计参数为：玻璃管膨胀系数αg=3.3×10-6/℃，杨氏模量Eg=64×109Pa，泊松比µg=0.2。金属板膨胀系数αm=4.8×10-6/℃，杨氏模量Em=140×109Pa，泊松比µm=0.3。封接温度点约为300℃，室温为25℃。 玻璃管的厚度tg=1.8mm，玻璃管的平均半径R=31.6mm，金属板的厚度tm=0.5mm。

玻璃是脆性材料，具有抗压不抗拉的特性，其抗拉强度通常为30～100MPa。玻璃管上最危险的应力出现在其表面上。

按设计参数计算得到玻璃－金属压封件中玻璃管外表面封接应力分布，如图3所示。

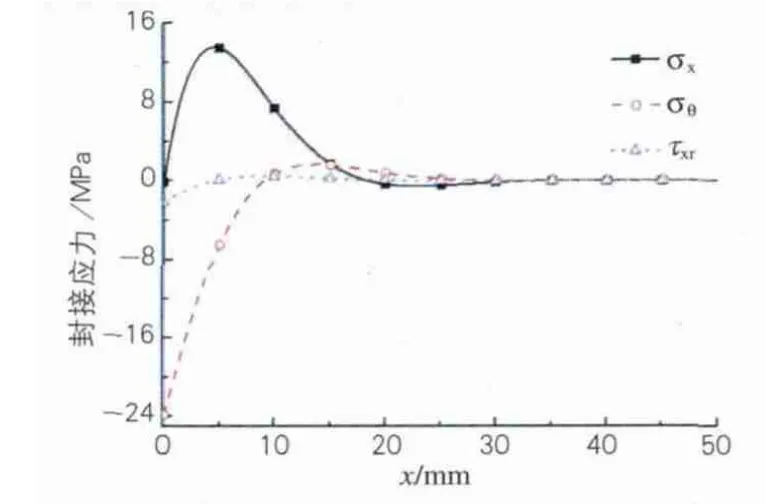
图3 玻璃-金属压封件的封接应力分布

将玻璃管材料更换为膨胀系数为αg=5.0×10-6/℃的玻璃，并且保持其他设计参数不变，这时玻璃管的膨胀系数比金属板的大，计算得到玻璃管内表面封接应力分布情况，如图4所示。

图4 玻璃膨胀系数对封接应力的影响

在图3、图4中正的应力值表示拉应力，负的应力值表示压应力。

从图3可知，当玻璃管膨胀系数比金属板小时，玻璃管外表面在靠近端面的位置，轴向应力σx主要表现为拉应力，而周向应力σθ、平均剪应力τxr主要表现为压应力。轴向应力σx的分布规律为先增大后减小，并迅速衰减，在距端面30mm后应力值基本为0。轴向拉应力最大值出现的位置约为距端面3.2mm处，最大值约为14MPa，远小于玻璃的抗拉强度，可认为该压封件的封接应力处于安全范围内。

由图4可知，当玻璃管膨胀系数略大于金属板时。玻璃管内表面在靠近端面的位置，轴向应力σx、周向应力σθ和平均剪应力τxr主要表现为拉应力。轴向应力σx仍表现为先增大后减小并迅速衰减为0的规律，但其最大值不到2MPa，出现在约距端面3.2mm处。周向应力的分布规律表现为迅速衰减并改变为压应力，最后衰减为0。周向拉应力的最大值约为3.4MPa，出现在端面处。对比图3、图4可知，在压封件中采用与金属板膨胀系数接近的玻璃管可极大地改善封接应力。

在目前的压封件中，通常玻璃管膨胀系数比金属板小。在这种情况下，最危险的应力是玻璃管外表面的轴向拉应力，其最大值多出现在距离端面几mm的位置。保持其他设计参数不变，分别改变玻璃管厚度、金属板厚度，得到轴向拉应力最大值的变化情况如图5、图6所示。

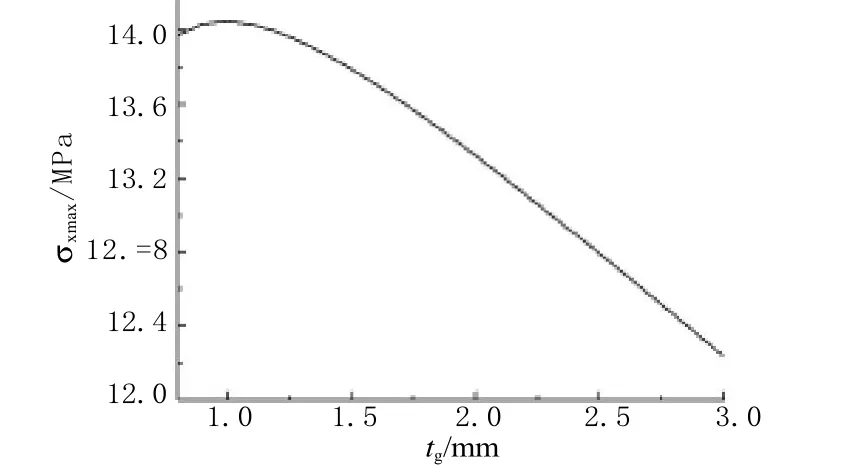
图5 轴向拉应力最大值随玻璃管厚度的变化

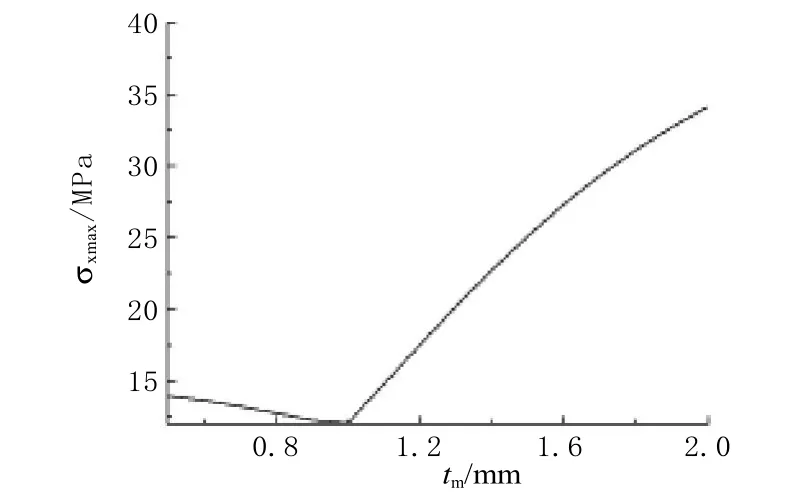
图6 轴向拉应力最大值随金属板厚度的变化

由图5可知，随着玻璃管厚度增加，轴向拉应力最大值会先略有增加，随后将不断减小，将玻璃管厚度增加为3mm时，轴向应力将减小约为12.2MPa。

金属板厚度增加对最大拉应力的影响情况较为特殊。随着金属板厚度的增加，玻璃外表面的最大轴向拉应力会有所减小，而玻璃管内表面端面处的最大轴向拉应力会不断增大。可引入一个判据η=2βM/P：当其小于0.41时，最大拉应力出现在玻璃管外表面上距端面一定距离处；当其大于0.41时，最大拉应力出现在玻璃管内表面端面处[2]。在图6中，当金属板厚度小于1mm时，η＜0.41，轴向拉应力的最大值出现在玻璃管外表面上，并且随着金属板厚度的增加而有一定程度的减小；当金属板厚度大于1mm时，η＞0.41，轴向拉应力的最大值出现在玻璃管内表面端面处，并且随着金属板厚度的增加而迅速增加；当金属板厚度为1mm时，η=0.41，玻璃管内外表面轴向拉应力的最大值相等。从图6可知，应尽可能使金属板的厚度满足η≤0.41，以保证压封件的安全。

最后再对玻璃管平均半径对轴向拉应力的最大值的影响进行讨论。保证其他设计参数不变，改变玻璃管的平均半径大小，计算得到轴向拉应力最大值随玻璃管平均半径变化曲线，如图7所示。由图7可知，玻璃管的半径增大会使轴向拉应力最大值增大，但增加幅度较小。

图7 轴向拉应力最大值随玻璃管平均半径的变化

四 讨论

根据板壳理论和平封模型计算了所设计的压封件的封接应力。根据设计参数计算得到的结果表明玻璃管中的最大轴向拉应力约为14MPa，压封件较为安全。

计算结果还表明，选用与金属膨胀系数接近的玻璃材料将能极大改善封接应力。适当的增加玻璃管的厚度可在一定程度上减小封接应力。金属板的厚度可尽量选择使玻璃管内外表面轴向拉应力最大值相同的值。玻璃管平均半径的大小对轴向拉应力最大值影响不大。

最后需要指出的是，在压封过程中采用了一种纯的低熔点金属料，在封接粘着后一段温度内具有良好的塑性，将会减小玻璃中的应力。因此实际压封件的封接应力相较文中的计算值应偏小，但不影响对封接应力分布规律的讨论，并且可进一步保证压封件的封接应力处于安全范围以内。

[1] 刘联宝, 杨钰平, 柯和春; 等. 陶瓷-金属封接技术指南[M]. 北京: 国防工业出版社, 1990.

[2] 殷志强, 柯春和. 陶瓷金属平面封接中的应力分析与计算[J].真空技术, 1980, (1): 7－19.