凝聚态、宏观量子效应和高温超导＊

张一方

（云南大学物理系，云南昆明 650091）

凝聚态、宏观量子效应和高温超导＊

张一方

（云南大学物理系，云南昆明 650091）

凝聚态物理是对称性破缺的产物，由此讨论Ising模型及其推广；探讨分形的应用和Hall效应；探索宏观量子效应和超流；探讨高温超导及其袋模型，联系于玻色－爱因斯坦凝聚（BEC），预言应该存在高温超流；讨论粒子－分子的类似性等，并总结宏观量子效应.

凝聚态物理；宏观量子效应；分形；Hall效应；超流；高温超导；玻色－爱因斯坦凝聚

1 对称性破缺，Ising模型及其推广

物理学最基本的原理是对称性原理，它包括广义守恒原理和对称性破缺［1］.凝聚态物理是对称性破缺的产物：晶体是平移对称性破缺；铁电体和反铁电体是空间反演对称性破缺；铁磁体和反铁磁体是时间反演对称性破缺；超流体与超导体是规范对称性破缺.对称性破缺是相变，意味着出现序参量不为0的有序相.

Ising模型［2］用Lie代数求出Onsager解，之后用无规行走法解，这应该可以推广Lie代数的解.它可以称顶点模型，联系于图论.Ising模型目前在n＝3时无严格解.Ising模型之难可能联系于长程力、新相互作用，此时配分函数、熵增等也许应当修改［3－5］.该模型是连续对称，描述各向异性的铁磁体，同时Heisenberg模型是离散对称，描述各向同性的铁磁体.二者应该类似Planck黑体辐射公式，是Wien和Rayleigh－Jeans公式的互补、结合.

有2个方向和2种可能的Ising模型，可以类似地应用于电子、质子等2个自旋方向的系统，如超导等中，或者2个方面彼此类比发展，且推广后应该可以描述任意2种物体混合的系统，如夸克－胶子，费米子－玻色子即超粒子等系统.此时都是二项式分布，数目极大时化为高斯或Poisson分布.

Potts模型是Ising模型的推广［6］，量子化矢量推广到更多的方向，所有相变都可以和Potts模型联系.Potts模型推广后应该可以描述任意N种物体混合的系统，Ising和Potts模型可以发展为分维D和复维Dz

［7－8］等.例如2＜D＜3，可以如此是因为粒子有一定的随机运动和振动.

一维Ising模型可以化为↑↑，↓↓，↑↓和↓↑4种，这相应于四象和符号动力学［9］中的LL，RR，LR，RL.因此可用矩阵力学和易理.三维Ising模型形式上可以类似推广，可以加外磁场H.

2 分形和量子Hall效应

凝聚态物理的分形主要包括：（1）随机分形，如阈值时的无限长渗流集团、线性高分子链和随机行走等.（2）有规分形模型，如Sierpenski篮子、地毯和海绵等.凝聚态物理中分形存在元激发称分形子（frac－ton）.自相似空间中至少需定义3种维数：欧氏d，分维D，分形子（光谱）维数.对Sierpenski篮子，d≥D≥.反常扩散、凝聚过程、吸附表面、奇异吸引子及准晶体都与分形有关.

由共价键结合的线型高分子链可以作为固定的随机分布曲线，其分维：（1）假定分子链节间没有相互作用，与Brown运动相似，用无规行走模型则D＝2.（2）假定分子链节间有相互作用，用自避免行走模型，结果与高分子Euclid维数有关，当d＝2时D＝4／3，当d＝3时D＝5／3.因此，物体的某些随机行为可以利用分形维数的性质描述.

凝聚态物理中，分形维数可以描述相变与临界现象中的某些标度不变性，与临界指数有密切关系.它还可以描述大分子的无规线团结构和渗流集团阈值等平衡态，被推广到若干远离平衡的不可逆生长过程，其显示出自相似的标度不变性质.

Jackiw和Rebbi研究Fermi场的孤子－磁单极子结构，暗示存在费米子数为1／2的孤子［10］.根据相对论场论研究一维无自旋费米场和有对称性破缺的玻色场的耦合时，得到具有分数电荷的激发态.对于能带被填满1／n的系统，孤子和反孤子激发态的电荷可能是±（e／n）的整数倍.但无自旋却是费米场就值得研究，这可能联系于超对称性或2种量子统计的统一［8，11］.

分数维形态的生长相应于自然界中的某些生长过程，如固体结晶，气泡在流体中的运动等.按照扩散限制凝聚（DLA）模型，一种无序不可逆生长过程可以产生一种特殊的分数维形态，可以解释一大类分形的形成过程.此模型是随机游动的聚合过程，导致分数维.现在已有多种随机生长模型，如果对晶体等能应用分维，则可以降低维数.

量子Hall效应在强磁场（13.9，18.9，10T）、极低温（1.8，1.3，4.2K）下出现，温度小于1K时还有分数量子Hall效应.分数量子Hall基态是具有很强相关的二维电子液体，高温超导体等与这类二维强相关电子体系密切联系.当T＝0.48K时，n→v＝p／q（q＝3，5，7，9，11，13，...），测量方法可用电或光学方法.

Hall电导率出现与电子密度无关的一定平台，其平台值是e2／h的整数倍.e2／h的测量精度可达百万分之一，这不是二维特有的现象，目前主要是Prange理论和Laughlin规范理论及阶层结构理论、集体激发的磁旋子理论、集体环交换理论、复合粒子理论.后者的“基本”粒子是由电子加m个磁通量子组成的复合粒子，m＝2k或2k＋1时为复合费米子或玻色子［12－14］.作为元激发的复合粒子服从分数统计，并带有分数电荷.它破坏了空间和时间反演对称性.分数量子Hall效应v＝1／3，1／5，1／7，...，有些类似倍周期分岔、混沌，可能联系于量子混沌，由此发展出非线性Schrodinger方程及其解.导电性对应费米子、电子，超导性对应玻色子的特性.

1987后发现偶分母分数态——5／2态.几种方法证实存在分数电荷，采用有效分数电荷e＊＝±e／q的准粒子作为载流单元，凝聚态中出现分数电荷的孤子.

3 超流、超导和宏观量子效应

流体是片流或湍流，决定于无量纲的雷诺数R＝Vrρ／μ，R＜1 000是片流，R＞2 000是湍流，2 000＞R＞1 000是过渡区.

宏观物体在极低温时特别易于显示量子性，如超导、超流等.而量子液体及其谱的概念实质上是宏观量子描述的基础，并且可以将金属的超导性理解为电子液体的超流性［15］.3He（费米子）和4He（玻色子）都具有超流性，说明其与统计性无关，可能联系于统计性统一［8，11］.但二者的超流温度不同，3He有2个超流相，类似组成Cooper对.元激发分为：（1）单粒子激发或称“准粒子”，通常是费米子；（2）集体激发，一般是玻色子.元激发可以统一理解物体的基本性质.

相互作用等可以化为热流体力学，并且因为作用时间极短，所以可以不考虑相互作用过程，而只考虑相互作用结果.进一步，结合复数维［7－8］、非线性理论.瞬时相互作用结果导致液态，唯象引入相互作用能，得到非线性方程.Gross－Pitaevskii超流方程即非线性Schrodinger方程.

各种宏观量子性应该相应于泛量子论［16－19］.在费米型量子液体中对应于元激发和准粒子，准粒子有自旋1／2，具有费米分布的形式，并可以引入有效质量［15］.对称的有玻色型量子液体中的元激发，具有整数角动量，服从玻色分布，准粒子是旋子［15］.

超导的Ginzburg－Landau方程为

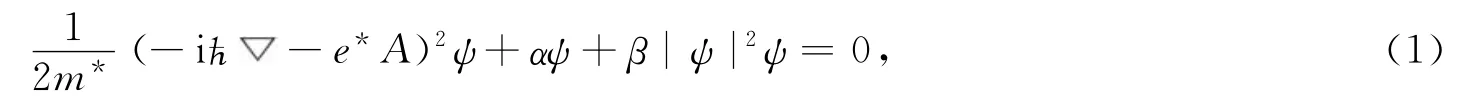
化简化为

（1），（2）式都是非线性方程.这是一种定态非线性Schrodinger方程，其孤子解可以用于解释超导，并且可以反之类似应用粒子相变的理论、模型、方法.

超导的Ginzburg－Landau方程推广对应协同学方程，协同相应于电子对，由此得到孤子.由非线性相互作用势可以导致相变及量子化现象.庞小峰《非线性量子力学理论》主要基于孤子，研究宏观量子效应，而笔者认为这是微观量子的集体（协同）效应或泛量子论［16－19］.笔者的非线性量子理论是一般的微观理论［8，20］，甚至泛非线性量子理论.王顺金的“人造量子系统的理论研究与代数动力学”研究非自洽量子系统［21］.这些研究对量子的基础理论，如测不准原理、Pauli不相容原理（PEP）、PCT等应该有所影响.

现代实验指出，宏观量子效应存在超导体方面，其中电流和磁通量都是宏观量子化的［15］，磁通量量子化为

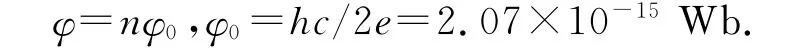
类似E＝nhv，则φ0～hv，即c／2e对应频率v，并有Josephson结.准经典能级为

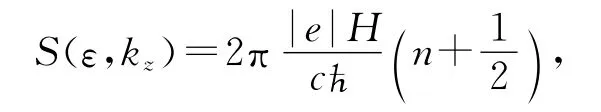
S（ε，kz）是量子化的［15］.超流是无阻尼的流动，类似惯性.超流体中，涡线的量子本质表现为闭合回路的环流值k和相应的速度v＝k／r只能具有一系列确定的离散值［15］.铁磁体中的磁矩运动方程d M／dt＝γK与经典电动力学方程的关系是M＝γħS，而γħ＝－（g｜e｜／2mc）［15］.

对泛量子论［16－19］，相变中Γ型孤子可以认为是一类广义量子及其跃迁，可以描述量子Hall效应.凡是阶梯的n个平台，其微分即产生（n－1）个孤子，其高度可能不同，对应于（n－1）个量子.而且多个孤子叠加就对应于多个量子叠加，也对应于（n＋1）个平台，可能量子Hall效应和孤子、波高度与跃迁度、h成正比.Hall效应如果是电子液体，则可以用KdV等非线性流体方程，或用泛非线性Schrodinger和非线性Dirac方程得到孤子解并合并.

目前宏观量子效应主要联系于低温，如分子磁体中的宏观量子效应等.可以用泛量子论等统一各种宏观量子效应.超流用一个宏观量子波函数描述，3He配对后在0.003K时也发现超流.量子Hall效应及其分数值暗含基本电荷是e的分数值，即e变为e／n，这是最明显的泛量子论.

Josephson结的隧道效应是宏观量子效应.超导BCS理论的Cooper对是电子的2倍，其及超流都是低温宏观整体量子效应，二者微观对应，可用Bose－Einstein（BE）统计解释，这似乎说明BE统计不符合热力学第2定理［3－6］.

对宏观量子现象，如果h＝1，若Heisenberg方程［15］为

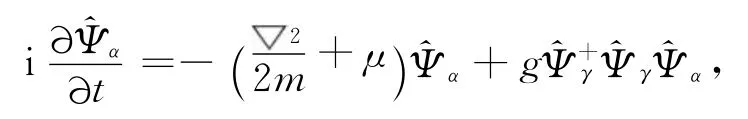
则p→p／h，E→E／h.相应的H＝1时泛量子理论就完全统一.

超流态与正常态的熵差［15］为

（3）式应该可正（T＞Tc时）可负（T＜Tc时）.

2001年《Nature》报道，Pfleiderer的实验证实对ZrZn2超导性和铁磁性统一［22］，Aoki等［23］证实铁磁性材料UrhGe在环境压力下具有超导性.

4 高温超导及其理论探索

迄今高温超导的理论解释仍然是现代物理学中一个没有解决的核心问题［24］.Anderson认为高温氧化物超导体正常态是非费米液体，其中电子的自旋与电荷元激发分开，且由层间Josephson隧穿退约束（deconfinement）推动高温超导的温度（driving force）.这表明高温超导有相应的Josephson效应.Laughlin同意Anderson理论中的核心思想，即对高温氧化物超导体费米液体原理失效［25］.他提出的高温超导理论为：服从分数统计粒子的理想气体是一种新型超导体［26］.高温超导理论的研究对20世纪凝聚态物理提出了基础性的课题［27］，即现有的20世纪凝聚态物理的重大成就——费米液体绘景（picture），由准粒子组成的气体结构，服从费米统计，应该进一步发展.这可能是Anderson提出的非费米液体或者是费米液体内在结构不同，

1987年章立源提出高温超导的双子系统体系（two subsystem assembly）理论，其中巡游载流子子系统（宽带态）与近局域载流子子系统（窄带态）之间有混杂相互作用（mixing interaction）.近局域载流子子系统可以形成对，由此提出Cooper对与Ogg对结合的超导理论［28］.1956年Cooper对电子距离为1 0－4cm，而1946年OGG R A［27］对电子距离为10－8cm，二者的数量级不同，Cooper对的形成必须在电磁屏蔽后.

对高温铜氧化物超导体正常态分析后可以得到［27］，其量子电子液体是介于非费米液体与费米液体之间的近费米液体.在高温下，偏离费米液体较大，继续降温时，向费米液体靠近，在临界时接近费米液体，但有新的特异.笔者认为此时PEP可能不成立［8，20，29］，应该对应于统一的统计性［11］.

高温超导具有若干新的特性，美国陶荣甲小组发现，在超导转变温度以下，加上电场后，高温超导颗粒聚成1个球，颗粒很多时聚成二三个球.这些球在正负电极之间以极高速度来回弹跳，作用力极其强大［30］.这是高温超导才具有的非常短的相干长度，即在非常近距离内的电子才可能相互结合成对.由此可能得到攻克高温超导机制的启示.准二维性是高温铜氧化物超导体的重要特征之一［27］，二维对应于任意子，所以应该研究任意子与高温超导的关系.

最近，Chen等［31］探讨了高温超导和自旋密度波不稳定性的关系，其中铁基高温超导，如L a（O1－xFx）FeAs成为研究一个重点，Rotter等［32］研究了温度为38K时砷化铁Ba1－XKXFe2As2的超导性，Ni等［33］研究了单晶Ba1－XKXFe2As2的各向异性热力学和输运性质，Yuan等［34］研究铁－砷（或铁－磷族）化合物在温度为56K时具有超导性，并具有各向同性.这与所有以前已知的各向异性的分层超导体不同.Zabolotnyy等［35］发现Ba1－XKXFe2As2的电子结构序与超导性共存，并且在室温时仍然存在.

高温超导理论除应用已知的费米子和玻色子外，还提出新的准粒子——空穴子（holon）和自旋子（spinon）等，实验结果证实高温超导体对金属中电子的权威理论Landau的费米液体理论不适用［36］，它联系于费米子凝聚，否定经典的BCS理论.而BCS理论的相互作用微弱，条件是ln（ħωD／Tc）≫1.当超导的临界温度Tc变大时，ħωD／Tc更小，因此泛量子理论［16－19］h→H变大是一条最简单的出路.Little［37］最早提出超导的强耦合机制，它也可能联系于PEP.Collins［38］讨论的高温超导电子“胶”不一定是共振，但本质上是磁性的.这可以结合协同学，类似激光产生.或者磁对应，结合广义相对论、运动场及其量子化后等的结果.

按照BCS理论［39－40］，超导的转变温度为

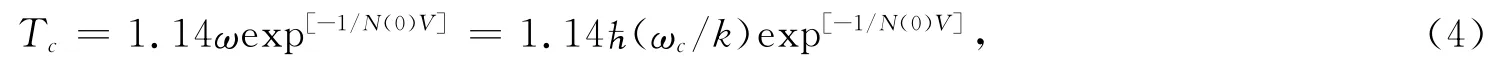
决定于相互作用强度N（0）V是弱的［41］.McMillan［42］提出强耦合超导的转变温度为

Ginzburg－Landau理论是唯象理论，如果（1）式中的各量相同，则Tc∝ħ（H）.这样就可以结合泛量子理论［16－19］.

1998年8 月发现，加压可以提高超导体的临界温度到200K.高温超导出现条纹状，镧系在40K有条纹，每3个有1个空格.条纹对应天文学Intermittency及分形.高温超导条件为掺杂0.15，无掺杂时长程有序，都涉及多体问题.可以结合非线性、混沌讨论类似协同学的宏观、微观、唯象理论，高温超导可能联系于纳米材料.

Goldstone等证明场论有超导解，理论上修改场论或其过程，结论就可能导出高温超导.远离平衡时长程关联，其增强就可以联系和描述高温超导，这是一种相变，其中电子相互作用是已知的或结合强相互作用，或是新的相互作用.超导应是微观量子论与多体电磁相互作用、随机理论等结合.

1987年M.Weinstein应用强子的SLAC袋模型［43］研究了高温超导现象，所得电压数及其比等结果与实验符合［44］，这为超导理论研究提出了一种新的方法.

Schrieffer等强调短程磁关联，并相应提出高温超导的自旋袋（spin bag）机制，其元激发是自旋袋，它具有固体物理中空穴的传统量子数，即电荷＋e和自旋1／2，但是存在很强的装饰效应（dressing effects）［45］.简单说，自旋袋元激发即是在自旋密度波序减少的环境中自陷的空穴，这个减少了的自旋波序区域与空穴同行（comoving）称为袋，这些袋元激发彼此间有吸引相互作用，在金属相中形成简并费米液体.其具有有效吸引势，产生S波配对超导电性［46－47］.

超导可以用电子对及推广为费米子对、袋等的理论解释.在此讨论高温超导的袋模型.电子对推广为袋，温度T高.袋模型作为禁闭夸克的一种机制，它与超导的类似早已被李政道等讨论过.推广强子袋模型中的σ场－夸克相互作用就相应于BCS理论中的声子－电子相互作用［48］.袋相应于费米球，即分布函数是Fermi－Dirac（FD）分布，此时方程是非线性的，其孤子解可以包括超导的负磁化率随温度的变化曲线及费米球的FD分布函数，特别对极限n→0的MIT袋以前就已获得类似FD分布的结果.

基于并推广这种方法，利用粒子物理中广泛研究过的袋模型及其相关的Friedberg和李政道的费米子场的非拓扑孤子理论［49－50］，可以得到高温超导理论的电子袋模型.此时超导现象的电子聚集作用已经由Cooper对推广为袋等，如果袋包含多个电子，则它相应于高温超导材料的电子原来就是紧密地结合在一起的，同时多个电子强耦合为袋也使超导临界温度应该较高.

假设高温超导对应于SLAC袋，则对应非线性方程为

对此非线性方程组可以用定性分析理论，并探讨其中的意义.一般的非线性方程应该有孤子解、混沌解，对应分维和时间的标度性，如果超导类似混沌，则多重产生及各种混沌模型都可以试图用于超导.

MIT袋是n→0的极限，（5），（6）式为线性方程，无非线性项，SLAC袋是n→∞的极限，则

其中x＝uv，y＝（u2－v2），τ＝2（ρ－1）.（7）式可化为

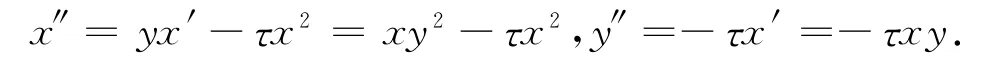
2种袋类似超导的2种图，这可能是Cooper对发展为多（2 N）个粒子的袋束缚态.

袋对应非线性sigma模型，可能相容、不相容与能量、对称性等有关.辛厚文认为超导类似性，对应自相似、分形，这可能联系于泛量子论［16－19］.二者推广则有多层，结构等改变，则相变点各不相同.不同的量子常数对BCS理论等将有所影响，如Tc∝ħ（H）.

低温、高温超导可能分别对应轻、重费米子体系，如此超导温度与某种质量等成比例.低温时电子组成Cooper对，高温时对某些重费米子体系Pauli相容，多个电子可组成袋，而高低温相对，低温超导是玻色子（费米子对），高温超导是任意子.

在一定的外部、内部条件下，所有粒子彼此相互结对，“凝聚”到单一状态，形成高度有序、长程相干态.因为结对，所以是Bose－Einstein动量凝聚，此时所有粒子的行为几乎完全相同，大量粒子的整体运动就和其中一个粒子的运动一样，只要用1个宏观波函数及相应的方程就能描述整个粒子体系.极低能时，费米子凝聚为准玻色子，此时PEP也不适用.

进一步，还可以应用与袋模型相关的理论及量子色动力学（QCD）的推广.

5 玻色－爱因斯坦凝聚（BEC）

对BEC，Bogoliubov，Brueckner和Sawada［51－52］把液氦作为有弱相互作用的玻色子组成的稀薄气体.实验已经确定在极低温时出现BEC.2005年6月已实现BEC的碱金属原子气有6种：1H，7Li，23Na，41K，85Rb，133Cs，全部是奇核子数.BEC的领军人物D.Kleppneer对理论不断提出新课题.

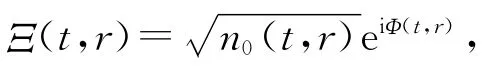
在实现BEC后，JIN D S在1999年制备了简并费米气体，并于2003年12月在（0～×107）℃得到费米凝聚（FDC）.冷却钾40原子，并称可能得到室温超导，但二者温度相差太大，值得进一步探讨，可能FDE先成对组成.

BEC发展产生BE激光、FD激光等［53］，探讨BEC（FDC）与激光、超导、超流的异同.它们温度极低且相互作用强，都与宏观量子态有关.BEC方程可以有孤子解，其正好描述这一集团（cluster）及相应的激光，这可能与PEP破坏有关.而高压时电荷成团（charge cluster）的奇异现象已经表明高压、高能时PEP被破坏［11，20，29］.当T≤Tc时，μ→0，则

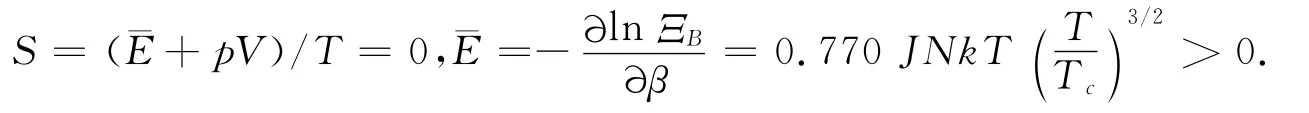
由此可知pV＝－¯E＜0，则p＜0，对应T＝0，但这不可能，所以在极低温时应该修正热力学，起码第三定律，这又联系于笔者对热力学原理的新探索［4－6］.

超流、超导都是BEC的集团效应，它们又相应于激光.笔者认为有高温超导就应该有高温超流，例如中子星内部超流体温度就达到108K，它可能类似毛细现象.超导和超流的机制和理论相似，前者的理论推广后应可以预言后者的转变温度，因此应该对高温超流进行理论探讨和实验预言.此外还有条件拓广后的激光.3方面的理论等可以互相类比，BEC作为任意子，由e－e相互作用组成，则PEP破缺，可能也有高温量子Hall效应.

6 结语

对介观（微尺度）热物理，田长霖提出时间、空间二维四区的方法，推广到三维（质量、相互作用、力场等）就可以建立三维八区理论.

拓扑学可以结合或者发展到流体、可塑性物质及凝聚态，它们就是可以任意变形的.R.Walser提出“超材料（metamaterial）”，Smith等［54］对此进行了具体研究，现在它已经成为引人注意的科学前沿.

Morse势及其能级对几乎所有分子给出非常准确的能级值［55］，其中分子能级对应GMO质量公式［8，56］，所以其是SU（3）及其一次破缺.只有少数分子才需要更精密的考虑，这对应于高阶修正.反之，分子理论应该可以应用粒子的理论和方法，如发展为振动－转动模型和动力学模型［8］，结构也是SU（2）和SU（N）对称性的破缺.

已知分子之间的引力与r2成反比，斥力与rn（3＜n＜11）之间成反比，可能粒子内部结构类似原子组成分子.简单分子对应基态粒子，复杂分子对应激发态粒子，不稳定分子对应共振态粒子.原子间只在分子距离内有效的化学力和核子间的核力都具有短程性、饱和性、交换性，所以，原子核组成结构可能类似分子组成结构.因此，分子、核、粒子三者之间可能具有某种类似性.

总之，比较玻色系统和费米系统可以得到：（1）玻色子，激光，对玻色型量子液体有超流，对一般玻色子是BEC.（2）费米子，电子成对导致超导，推广为任何费米子成对，此时稳定就可能形成激费米子［36］；而且可以产生费米子凝聚（FDC）.（3）稳定的光子形成激光，其余激玻色子不稳定［53］.电子对形成超导，稳定的中微子对vv在de Broglie光子熔合模型中相应光子［57－58］，pp，pn，nn就是原子核等.条件也不一定是低温，如对核，已经导致强相互作用等新性质，其余粒子不稳定.进一步可以是各种原子、分子等分为玻色子型的凝聚，或者费米子型的成对凝聚，甚至可以推广到最一般情况，阴阳配对，及阴阴、阳阳配对，并且凝聚.

［1］ 张一方.从量子力学－相对论到物理学的基本原理和Noether定理的推广［J］.云南大学学报，2007，29（4）：375－381.

［2］ 雷克L E.统计物理现代教程［M］.黄 畇，译.北京：北京大学出版社，1983.

［3］ 张一方.孤立系统的内部机制和热力学第二定律局限性的新探索［M］／／喻传赞.熵、信息与交叉科学.昆明：云南大学出版社，1994：53－60.

［4］ ZHANG Yi－fang.Possible Decrease of Entropy Due to Internal Interactions in Isolated Systems［J］.Apeiron，1997，4（4）：97－99.

［5］ ZHANG Yi－fang.Entropy，Fluctuation Magnified and Internal Interactions［J］.Entropy，2005，7（3）：190－198.

［6］ WU F Y.The Potts Model［J］.Rev.Mod.Phys.，1982，54（1）：235－268.

［7］ 张一方.粒子的分形模型，复数维及其意义［J］.大自然探索，1988，7（2）：21－23.

［8］ 张一方.粒子物理和相对论的新探索［M］.昆明：云南科技出版社，1989.

［9］ 郑伟谋，郝柏林.实用符号动力学［M］.上海：上海科技教育出版社，1994.

［10］ JACKIW R，REBBI C.Solitons with Fermion Number 1／2［J］.Phys.Rev.，1976，D13（12）：3 398－3 409.

［11］ ZHANG Yi－fang.High Energy Behavious of Particles and Unified Statistics［J］.Hadronic J.，1984，7（5）：1 118－1 133.

［12］ CHANG C－Zu，ZHANG J，XUE Qi－kun，et al.Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator［J］.Science，2013，340（6 129）：167－170.

［13］ JAIN J K，KIVELSON S A，TRIVEDI N.Scaling Theory of the Fractional Quantum Hall Effect［J］.Phys.Rev.Lett.，1990，64（11）：1 297－1 300.

［14］ JAIN J K.Theory of the Fractional Quantum Hall Effect［J］.Phys.Rev.，1990，B41（11）：7 653－7 665.

［15］ 栗弗席兹E M，皮塔耶夫斯基.统计物理学II（凝聚态理论）［M］.王锡绂，译.北京：高等教育出版社，2008.

［16］ 张一方.Titius－Bode定则的发展，天体量子论和泛量子理论［J］.云南大学学报：自然科学版，1993，15（4）：297－303.

［17］ ZHANG Yi－fang.Development of Titius－Bode Law and the Extensive Quantum Theory［J］.Physics Essays，2002，1 5（2）：133－137.

［18］ 张一方.泛量子理论的发展及其在生化和物理中的应用［J］.吉首大学学报：自然科学版，2006，27（5）：34－38；48.

［19］ ZHANG Yi－fang.Quantized Phenomena in Astronomy and Astronomic Quantum Theory［J］.Int.J.Sciences，2 013（2）：58－73.

［20］ ZHANG Yi－fang.Test of Pauli’s Exclusion Principle in Particle Physics，Astrophysics and Other Fields［J］.Hadronic J.，1999，22（3）：257－268.

［21］ CHANG Yi－fang.Nanophysics，Macroscopic Quantum Phenomena and Extensive Quantum Theory［J］.International Journal of Nano and Material Sciences，2013，2（1）：9－24.

［22］ PFLEIDERER C，UHLARZ M，HAYDEN S M，et al.Coexistence of Superconductivity and Ferromagnetism in the DBand Metal ZrZn2［J］.Nature，2001，412（6 842）：58－61.

［23］ AOKI D，HUXLEY A，RESSOUCHE E，et al.Coexistence of Superconductivity and Ferromagnetism in UrhGe［J］.Nature，2001，413（6 856）：613－616.

［24］ ANNETT J F.Superconductivity，Superfluids and Condensates［M］.Oxford：Oxford University Press，2004.

［25］ LAUGHLIN R B.The Relationship Between High－Temperature Superconductivity and the Fractional Hall Effect［J］.Science，1988，242（4 878）：525－533.

［26］ LAUGHLIN R B.Superconducting Ground State of Noninteractingparticles Obeying Fractional Statistics［J］.Phys.Rev.Lett.，1988，60（25）：2 677－2 680.

［27］ 章立源.超导理论［M］.北京：科学出版社，2003.

［28］ ZHANG Li－yuan，ZHOU Yun－song.On the Combination of the Cooper Pair and the Ogg Pair in the High－TCSuperconductor［J］.Physica，1992，C198（3－4）：378－382.

［29］ ZHANG Yi－fang.Some Possible Tests of the Inapplicability of Pauli’S Exclusion Principle［J］.Hadronic J.，1984，7（6）：1 469－1 473.

［30］ TAO R，ZHANG X，TANG X.Formation of High Temperature Superconducting Balls［J］.Phys.Rev.Lett.，1999，83（26）：5 575－5 578.

［31］ CHEN G F，LI Z，WU D，et al.Superconductivity at 41Kand Its Competition with Spin－Density－Wave Instability in Layered CeO1－XFXFeAs［J］.Phys.Rev.Lett.，2008，100（24）：247 002.

［32］ ROTTER M，TEGEL M，JOHRENDT D.Superconductivity at 38Kin the Iron Arsenide Ba1－XKXFe2As2［J］.Phys.Rev.Lett.，2008，101（10）：107 006.

［33］ NI N，BUD’KO S L，KREYSSIG，et al.Anisotropic Thermodynamic and Transport Properties of Single Crystalline Ba1－XKXFe2As2（X＝0and 0.45）［J］.Phys.Rev.，2008，B78（1）：014 507.

［34］ YUAN H Q，SINGLETON J，BALAKIREV F F，et al.Nearly Isotropic Superconductivity in（Ba，K）Fe2As2［J］.Nature，2009，457（7 229）：565－568.

［35］ ZABOLOTNYY V B，INOSOV D S，EVTUSHINSKY D V，et al.（π，π）Electronic Order in Iron Arsenide Superconductors［J］.Nature，2009，457（7 229）：569－572.

［36］ HILL R W，PROUST C，TAILLEFER L，et al.Breakdown of Fermi－Liquid Theory in a Copper－Oxide Superconductor［J］.Nature，2001，414（6 865）：711－715.

［37］ LITTLE W A.Possibility of Synthesizing an Organic Superconductor［J］.Phys.Rev.，1964，134（6A）：1 416－1 424.

［38］ COLLINS G P.高温超导电子“胶”［J］.科学，2004（7）：9－10.

［39］ BARDEEN J，COOPER L N，SCHRIEFFER J R.Microscopic Theory of Superconductivity［J］.Phys.Rev.，1957，1 06（1）：162－164.

［40］ BARDEEN J，COOPER L N，SCHRIEFFER J R.Theory of Superconductivity［J］.Phys.Rev.，1957，108（5）：1 175－1 204.

［41］ 章立源，张金龙，崔广霁.超导物理学［M］.北京：电子工业出版社，1995.

［42］ MCMILLAN W L.Transition Temperature of Strong－Coupled Superconductors［J］.Phys.Rev.，1968，167（2）：3 31－344.

［43］ BARDEEN W A，CHANOWITZ M S，DRELL S D，et al.Heavy Quarks and Strong Binding：A Field Theory of Hadron Structure［J］.Phys.Rev.，1975，D11（5）：1 094－1 136.

［44］ WEINSTEIN M.Are the New High Temperature Superconductor Strong Coupling Systems？［J］.SLAC.Pub.，1987，4 272：1－12.

［45］ SCHRIEFFER J R，WEN X G，ZHANG S C.Dynamical Spin Fluctuations and the Bag Mechanism of High－TCSuperconductivity［J］.Phys.Rev.，1989，B39（16）：11 663－11 679.

［46］ KAMPF A，SCHRIEFFER J R.Pseudogaps and the Spin－Bag Approach to High－TCSuperconductivity［J］.Phys.Rev.，1990，B41（10）：63 996 408.

［47］ KAMPF A，SCHRIEFFER J R.Spectral Function and Photoemission Spectra in Antiferromagnetically Correlated Metals［J］.Phys.Rev.，1990，B42（13）：7 967－7 974.

［48］ 李政道.粒子物理和场论简引［M］.汤拒非，译.北京：科学出版社，1984.

［49］ FRIEDBERG R，LEE T D.Fermion－Field Nontopological Solitons［J］.Phys.Rev.，1977，D15（6）：1 694－1 711.

［50］ FRIEDBERG R，LEE T D.Fermion－Field Nontopological SolitonsⅡ.Models for Hadrons［J］.Phys.Rev.，1977，D 16（4）：1 096－1 118.

［51］ BRUECKNER K A，SAWADA K.Bose－Einstein Gas with Repulsive Interactions：General Theory［J］.Phys.Rev.，1957，106（6）：1 117－1 127.

［52］ BRUECKNER K A，SAWADA K.Bose－Einstein Gas with Repulsive Interactions：Hard Spheres at High Density［J］.Phys.Rev.，1957，106（6）：1 128－1 135.

［53］ 张一方.电磁学和光学中的某些问题及其发展［C］／／数学力学物理学高新技术研究进展——2006（11）卷.成都：西南交通大学出版社，2006：274－278.

［54］ SCHURIG D，MOCK J J，SMITH D R，et al.Metamaterial Electromagnetic Cloak at Microwave Frequencies［J］.Science，2006，314（5 801）：977－980.

［55］ 泡令L，威耳孙E B.量子力学导论［M］.陈洪生，译.北京：科学出版社，1964.

［56］ ZHANG Yi－fang.From Emergence String to Mass Formulas of Hadrons and Symmetric Lifetime Formulas of Hadrons［J］.Int.Rev.Phys.，2012，6（3）：261－268.

［57］ ZHANG Yi－fang，YU C Z.New Model on Solar Neutrino［C］.Proc.24th ICRC.，1995：1 212－1 215.

［58］ 张一方，喻传赞.De Broglie－Ross模型和太阳中微子问题［J］.益阳师专学报，1998，15（5）：20－23.

（责任编辑 陈炳权）

Condensed States，Macroscopic Quantum Effects and High－TcSuperconductivity

ZHANG Yi－fang
（Department of Physics，Yunnan University，Kunming 650091，China）

All condensed state physics is the result of breaking symmetry.Ising model and its extension are thus discussed.Then the fractal applications and Hall effect are researched.Thirdly，the macroscopic quantum effects and superfluidity are explored.Fourthly，the high－Tcsuperconductivity is discussed，and its bag model is investigated.These are related with the Bose－Einstein condensation（BEC），and the author predicts that the high－Tcsuperfluidity should exist.Finally，the similarity between particles and molecules is discussed，and the macroscopic quantum effects are summarized.

condensed state physics；macroscopic quantum effect；fractal；Hall effect；superfluidity；high－Tcsuperconductivity；BEC

O469

A

10.3969／j.issn.1007－2985.2013.03.008

1007－2985（2013）03－0031－08

2013－03－25

国家自然科学基金资助项目（11164033）

张一方（1947－），男，云南昆明人，云南大学物理系教授，主要从事理论物理研究.