带非连续解椭圆问题的3次Hermite配点方法＊

姜英军，邹莳珺

（长沙理工大学数学与计算科学学院，湖南长沙 410114）

带非连续解椭圆问题的3次Hermite配点方法＊

姜英军，邹莳珺

（长沙理工大学数学与计算科学学院，湖南长沙 410114）

使用3次Hermite配点方法，对一类带有非连续解的椭圆问题进行数值求解，將其解的不连续点取作网格节点，解在不连续点的左右极限作为未知量，结合解在不连续点的“跳跃”信息对原问题进行离散.数值实验表明此方法的收敛阶为O（h4）.

椭圆问题；Hermite插值；配点方法

1 具有非连续解的椭圆问题

考虑求解一维椭圆问题［1－2］

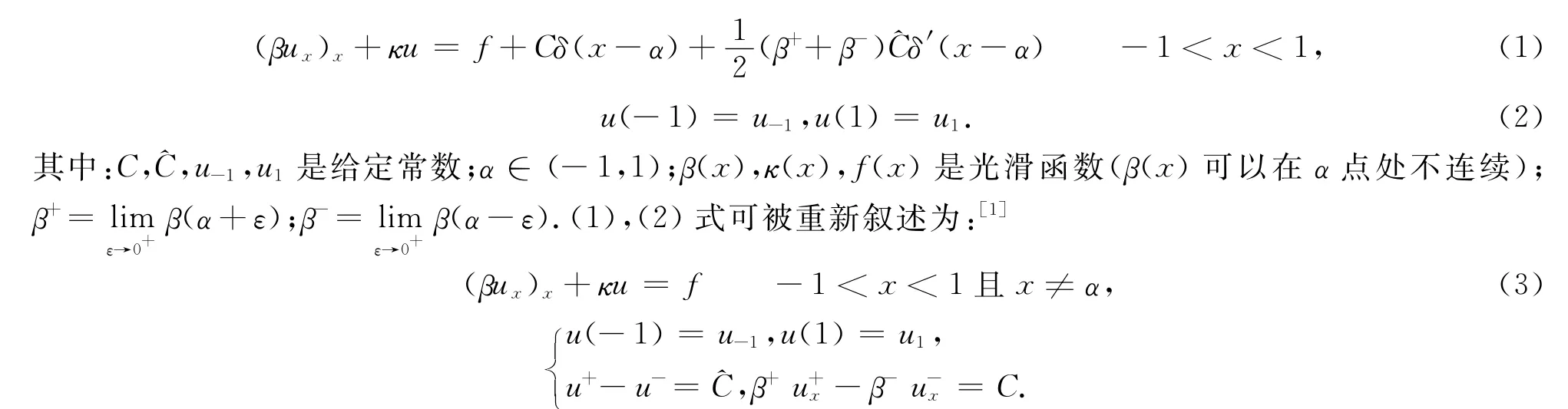
（1）式的唯一解在除去x＝α点外是光滑函数，文献［1］给出了对其求解的2阶收敛性算法.文中将使用文献［3］中所提出的求解偏微分方程的埃尔米特配点算法对（1）式进行数值求解.

2 Hermite配点方法

对［－1，1］剖分为－1＝x0＜x1＜...＜xm＝μ＜...＜xN＝1，使用一个分段三次多项式v（x）作为u（x）的近似，v（x）的定义为

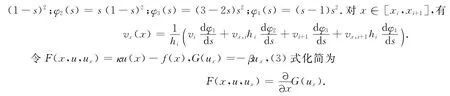
在［xi，xi＋1］上将（3）式中u换成v，并对区间［xi，xi＋1］的2个半区间进行积分可得

（6），（7）式即为（1），（2）式的离散问题.

3 数值实验

求解下面问题：

此问题精确解为

表1中列出实验结果，其中eN表示近似解的无穷范数误差，即eN＝‖u－v‖∞，r＝log（eN／eN－4）／log（N／（N－4））.实验结果表明，该算法具有4阶收敛性.

表1 数值实验结果

4 结语

设计了一种有效的数值方法求解带不连续解的椭圆型问题，并将解的不连续点作为网格节点，解在不连续点的左右极限作为未知量，结合解在不连续点的“跳跃”信息得到了原问题的离散格式.实验表明这种方法是有效的，具有4阶收敛性.应用此方法求解带有非连续解的抛物问题［4－5］.

［1］ LEVEQUE R J，LI Zhi－lin.The Immersed Interface Method for Elliptic Equations with Discontinuous Coefficients and Singular Sources［J］.SIAM Journal on Numerical Analysis，1994，31：1 019－1 044.

［2］ TIKHONOV A N，SAMARSKII A A.Homogeneous Difference Schemes［J］.USSR Computational Mathematics and Mathematical Physics，1962（1）：5－67.

［3］ HUANG W Z，RUSSELL R D.A Moving Collocation Method for the Numerical Solution of Time Dependent Differential Equations［J］.Applied Numerical Mathematics，1996，20：101－116.

［4］ MA Jing－tang，JIANG Ying－jun.Moving Mesh Methods for Blow up in Reaction－Diffusion Equations with Traveling Heat Source［J］.Journal of Computational Physics，2009，228：6 977－6 990.

［5］ 马敬堂，姜英军.带插值的自适应网格重构算法求解带移动热源的反应扩散方程的理论分析［J］.中国科学，2011，41：235－251.

（责任编辑 向阳洁）

Cubic Hermite Collocation Method for Solving the Elliptic Problem with a Discontinuous Solution

JIANG Ying－jun，ZOU Shi－jun
（Department of Mathematics and Computing Science，Changsha University of Science and Technology，Changsha 410114，China）

The cubic Hermite collocation method is used in discretization of an elliptic problem with a discontinuous solution.The discontinuous points of the solution are taken as grid points，the left and right limits of the solution at the discontinuous points as unknowns.The jumpings of the solution at the discontinuous points are combined to dicrete the original problem.The test indicates that the method has the convergence of order O（h4）.

elliptic problem；Hermite interpolation；collocation method

O175.26

A

10.3969／j.issn.1007－2985.2013.03.004

1007－2985（2013）03－0016－03

2013－03－14

国家自然科学基金资助项目（10901027）

姜英军（1975－），男，湖南长沙人，长沙理工大学数学与计算科学学院副教授，博士，主要从事微分方程数值解研究.