曲面上曲线的测地曲率向量的注记＊

邢家省，张光照

（1.北京航空航天大学数学与系统科学学院，数学、信息与行为教育部重点实验室，北京 100191；2.河南经贸职业学院技术科学系，河南郑州 450000）

曲面上曲线的测地曲率向量的注记＊

邢家省1，张光照2

（1.北京航空航天大学数学与系统科学学院，数学、信息与行为教育部重点实验室，北京 100191；2.河南经贸职业学院技术科学系，河南郑州 450000）

指出测地曲率向量的几何来源意义，给出测地曲率计算公式和刘维尔公式的直接推导.

测地曲率向量；测地曲率；几何意义；刘维尔公式

关于曲面上曲线的测地曲率向量和测地曲率的定义，文献［1－4］中采用的是直接给出了表述定义的式子，没有给出导致这种定义的几何意义来源，使人感到过于突然.笔者指出在导出曲面的第二基本形式的几何意义时，蕴涵了测地曲率向量的几何来源和意义，这样就符合人们的认识发现规律，有利于教学理解.对测地曲率的计算公式和刘维尔公式，也给出了直接的推导过程.

1 测地曲率向量的几何来源

在导出曲面的第二基本形式的几何意义时蕴涵了测地曲率向量的几何来源［1－2］.

设曲面Σ的参数方程为Σ：r＝r（u，v），（u，v）∈Δ.若r（u，v）具有2阶连续偏导数，则称曲面Σ为C2类曲面.现在任固定曲面Σ上一点P（u，v），并设TP为曲面Σ在P点的切平面.曲线Γ：u＝u（s），v＝v（s），或r＝r（u（s），v（s））是Σ上过P点的一曲线，其中s是曲线的自然参数.设Q是曲线Γ上在P点邻近的一点，P和Q点分别对应自然参数s和s＋Δs，即P和Q点的向径分别为r（s），r（s＋Δs）.

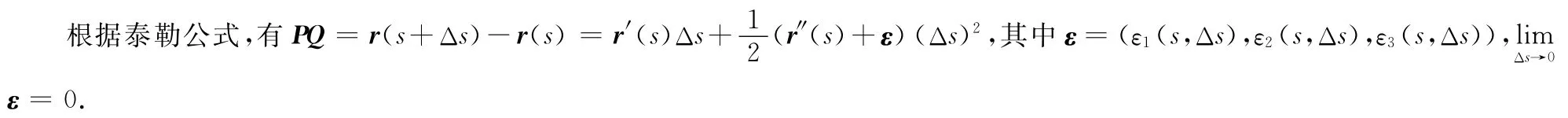
设n为曲面Σ在P点的单位法向量，由Q作切平面TP的垂线，垂足为Q1，则有Q1Q＝δn，其中δ是Q点到切平面TP的有向距离.

因为Q1P·n＝0，n·r′＝0，所以有

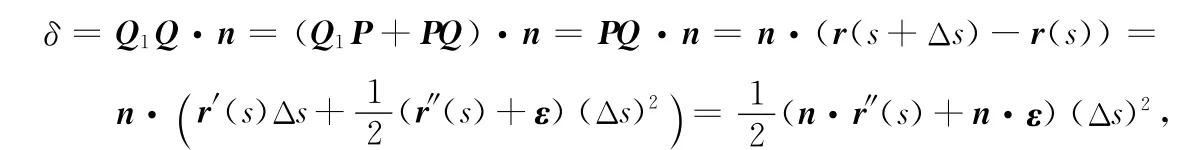
由此导致引入了曲面的第二基本形式的定义及其几何意义［1－2］.

考虑曲线在切平面上的投影向量与在切线上投影向量的接近程度，

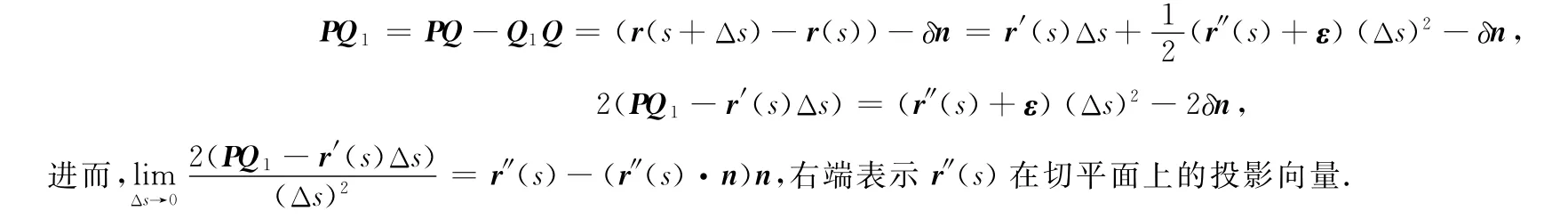
由此导致了测地曲率向量定义来源的几何意义，并能解释测地线的几何意义.

曲面上沿曲线的切向量场的绝对微分的思想和Levi－Civita平行移动概念也可认为来源于此.

2 测地曲率向量的定义

以α表示曲线Γ上P点处的单位切向量，以β表示曲线Γ上P点处的主法向量，γ是副法向量.

定义1 曲面Σ上曲线Γ在P点的单位切向量的导向量α′（s）在切平面TP上的投影向量τP＝α′（s）－（α′（s）·n）n，称为曲线Γ在P点的测地曲率向量.称Dα＝dα－（dα·n）n为α（s）沿曲线Γ的绝对微分.

根据伏雷内公式，有r″（s）＝α′（s）＝k（s）β（s），其中k（s）是曲线Γ在P点的曲率.称k（s）β（s）为曲率向量.故有τP＝r″（s）－（r″（s）·n）n，τP＝kβ－（kβ·n）n.

以θ表示β与n的夹角，则曲面Σ在P点的切方向α上的法曲率是kn＝kcosθ＝k（s）β（s）·n＝α′（s）·n，显然α′（s）－（α′（s）·n）n与n，α都垂直.

命ε＝n×α，则α，ε，n是彼此正交的单位向量，并且构成一右手系.α′（s）在切平面TP上的投影向量也就是α′（s）在ε上的投影向量.

定义2［1－4］曲面Σ上曲线Γ的切向量的导向量α′（s）在ε上的投影向量τP＝（α′（s）·ε）ε，称为曲线Γ在P点的测地曲率向量.

显然有τP＝α′（s）－（α′（s）·n）n＝kβ－（kβ·n）n，τP＝kβ－knn，kβ＝knn＋τP，τP＝（r″（s）·ε）ε.

定义3［1－4］将r″（s）·ε称为曲线Γ在P点的测地曲率，记作kg，kg＝r″（s）·ε＝τP·ε.

显然有τP＝kgε，kβ＝knn＋τP＝knn＋kgε.

定义4［1－6］将ε′（s）在n上的投影ε′（s）·n称为曲线Γ在P点的测地挠率，记作τg，τg＝ε′（s）·n.

3 测地曲率向量的几何意义

定理1［2，5］曲面Σ上曲线Γ在P点的测地曲率向量τP，即为Γ在切平面TP上的投影曲线Γ0在P点的曲率向量.

证明 设曲线Γ的方程是r＝r（s），n是曲面Σ在P点的法向量.

将曲线Γ投影到切平面TP上，得到TP上的一条曲线Γ0，其方程为ρ（t）＝r（s＋t）－（（r（s＋t）－r（s））·n（s））n（s），参数t未必是曲线Γ0的弧长参数，

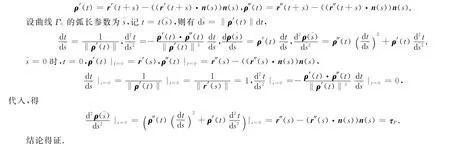
4 曲面上曲线的测地曲率与曲线的曲率和法曲率的关系

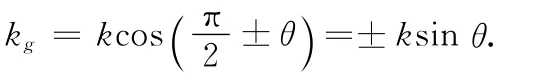
5 曲面上曲线的测地曲率的一般计算公式的直接推导

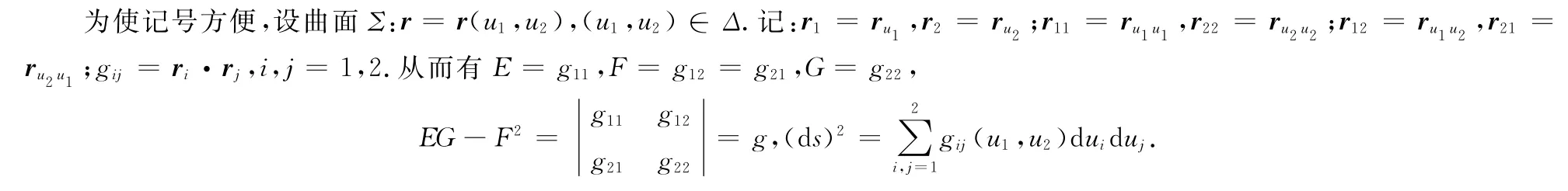
设Γ是曲面Σ上的一条曲线，其参数方程为u1＝u1（s），u2＝u2（s），或r＝r（u1（s），u2（s））＝r（s），这里s是该曲线的自然参数.

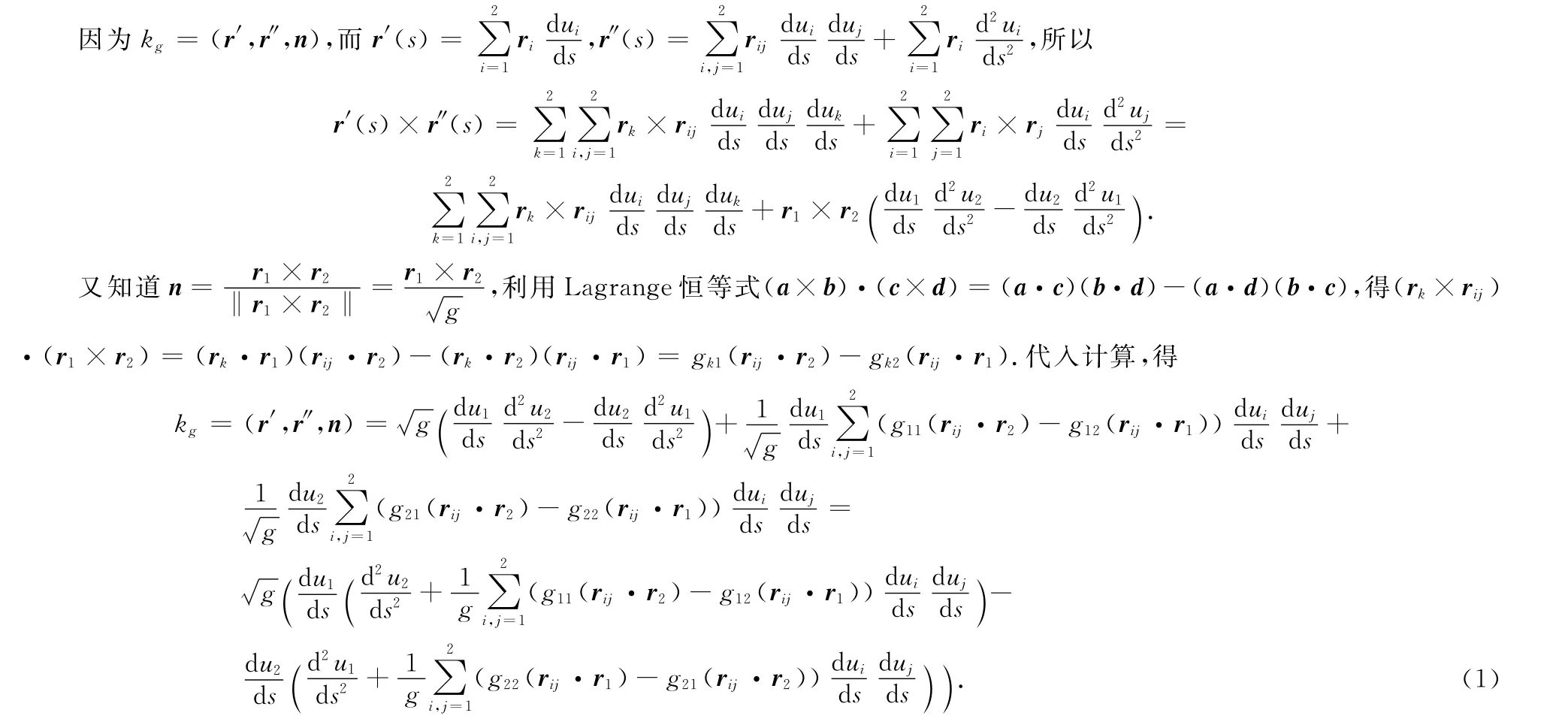
以上是测地曲率的一般计算公式，方便于直接使用.

现仅用向量运算法的直接推导过程给出测地曲率的一般计算公式.这与利用曲面论的基本方程式推导出测地曲率的计算公式是一致的［1－4］.

事实上，由曲面论的基本方程式中的记号［1－4］，

6 正交坐标曲线网下测地曲率的Liouville公式的直接推导过程

对于曲面r＝r（u1，u2）上的坐标曲线构成正交网时，有

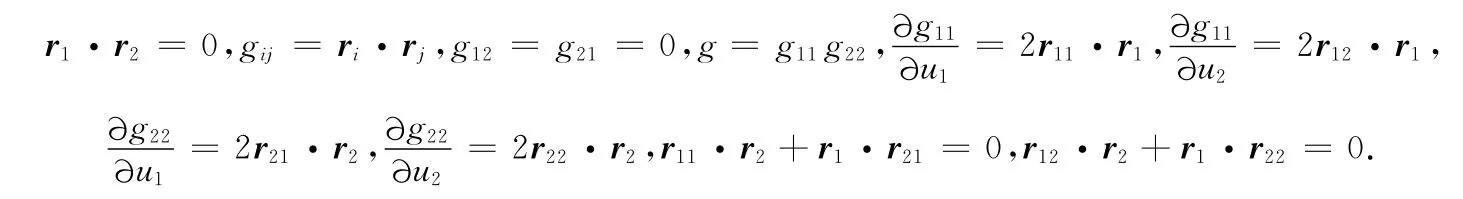
代入测地曲率的一般计算公式（1）中，整理后得

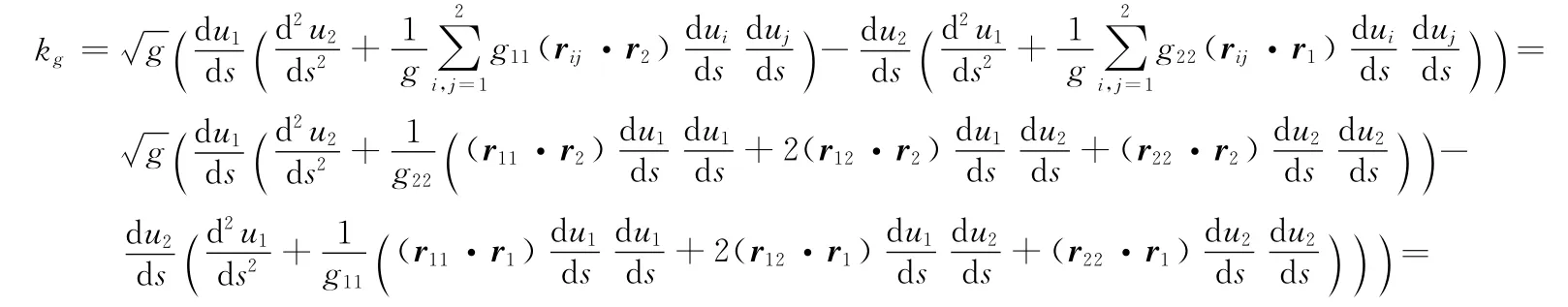
对于曲面r＝r（u，v）上的坐标曲线构成正交网时，u＝u1，v＝u2，E＝g11，G＝g22，于是

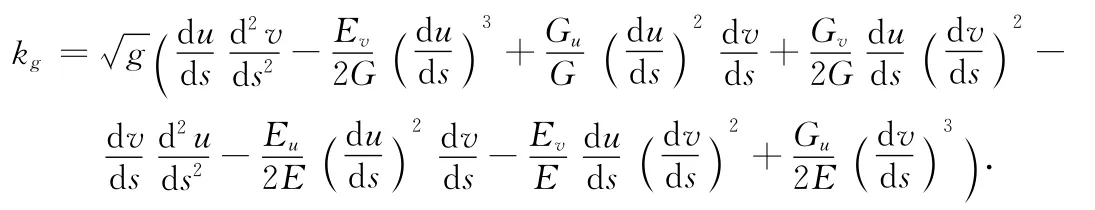
令曲线的切方向与ru的夹角为θ，则有

这个公式称为刘维尔（Liouville）公式.

文献［1］中指出的由（2）式可以推导出（5）式，计算过程将会是繁杂的.文献［2－3］为推导出（5）式，采用了另外的直接方法，掩盖了由（2）式到（5）式的关系转换.笔者发现的利用（1）式推导出（5）式是简单直接的.文献［7］给出了关于曲面上法曲率的最值的直接求法和性质.

［1］ 梅向明，黄敬之.微分几何［M］.第4版.北京：高等教育出版社出版，2008：82－84；146－149.

［2］ 陈维桓.微分几何［M］.北京：北京大学出版社，2006：139－143；229－241.

［3］ 彭家贵，陈 卿.微分几何［M］.北京：高等教育出版社，2002：43－47；110－117.

［4］ 马 力.简明微分几何［M］.北京：清华大学出版社，2004：27－38；76－81.

［5］ 陈维桓.微分几何例题详解和习题汇编［M］.北京：高等教育出版社出版，2010：171－219.

［6］ 邢家省，王拥军.曲面上曲线的测地挠率的计算公式及其应用［J］.聊城大学学报：自然科学版，2012，25（3）：1－4.

［7］ 邢家省.法曲率最值的直接求法［J］.吉首大学学报：自然科学版，2012，33（4）：11－15.

（责任编辑 向阳洁）

Note About Geodesic Curvature Vector of Curves on a Surface

XING Jia－sheng1，ZHANG Guang－zhao2
（1.Department of Mathematics，LMIB of the Ministry of Education，Beihang University，Beijing 100191，China；
2.Department of Technology Science，He’nan Economy ＆Trade Vocational College，Zhengzhou 450000，China）

The authors give the geometric meaning of the geodesic curvature vector，and a direct derivation method about the calculation formula of geodesic curvature and Liouville formula is obtained.

geodesic curvature vector；geodesic curvature；geometric meaning；Liouville formula

O186.11

A

10.3969／j.issn.1007－2985.2013.04.002

1007－2985（2013）04－0007－04

2012－12－03

国家自然科学基金资助项目（11171013）

邢家省（1964－），男，河南泌阳人，北京航空航天大学副教授，博士，主要从事偏微分方程、微分几何研究.