一种五轴侧铣加工进给速度的优化方法*
胡命华,江 磊,丁国富,马术文,阎开印
(西南交通大学机械工程学院先进设计与制造技术研究所,成都 610031)
0 引言
零件的工作表面质量与零件的加工精度、磨合性质、密封性能、振动和噪声等都有着很重要的关系。在数控加工编程过程中,经常将数控程序的进给速度设定为恒定的值。造成在刀具轨迹变化的情况下,切削加工过程中的面积去除率会出现较大波动,从而导致材料去除率和切削力的波动,增加切削加工过程中的不稳定性,降低工件的表面质量。
在进给速度和面积去除率的优化方面,国内外学者进行了相关的研究。W.P.Wang[1]计算每一数控程序段执行过程中去除材料的体积,并用该体积值来估算切削负载和平均力,据此调整每一数控程序段的进给速度,使其满足加工约束条件和生产率最大化。Yamazaki[2]建立了进给速度与材料去除体积的函数,实现了进给速度的优化。清华大学Z.Z.Li[3]等利用材料去除率来获得平均功率和平均切削力,进而对数控程序的进给速度进行优化。Bae[4]建立了数控加工过程几何仿真模型,研究了端铣削过程材料去除率与刀具路径的关系,并通过实验建立了铣削力与材料去除率的关系数据库,以此作为进给速度优化的依据。Guzel等[5]通过切削力的模糊适应控制策略及CNC控制系统来调整进给速度,以获得较高的材料去除率。北航彭海涛[6]等由设定的峰值力确定出材料去除率目标值,根据每段刀具轨迹的实际切削体积计算出相应的进给速度。翟玉山等[7]以材料去除率为约束来优化大型汽车及覆盖件模具二维数控铣削的进给速度。田华利[8]通过计算三轴数控精加工过程中的面积去除率来选择和优化走刀方式,从而提高加工效率。陈志同、张保国[9]等提出并利用体积价值系数、面积价值系数、体积去除率和面积去除率建立以单位时间利润率或单位时间利润为目标函数的优化模型,解决了加工质量、加工难度、加工效率、加工成本和加工利润之间的权重确定问题。陈婷婷[10]在限定的刀具寿命前提下,以最大面积去除率、最短加工时间、最低生产成本为优化目标对精铣削加工参数进行优化,提高了面积去除率,减少了加工时间。
以上关于进给速度优化的研究主要针对三轴数控加工或五轴端铣加工,而针对五轴侧铣加工的相关研究尚未引起足够的重视。面积去除率的研究大多以平均的面积去除率来对切削过程进行优化,未能针对每一段数控程序进行面积去除率的计算,且面积计算方法不够精确。针对这些问题,本文提出一种针对五轴侧铣加工工艺的进给速度优化方法。该方法通过构建五轴侧铣刀轴扫掠轨迹模型,较为精确的计算每一段数控程序的有效刀轴扫掠面积率,从而调整数控程序段的进给速度,使得五轴侧铣精加工过程保持稳定的面积去除率,提高加工过程中的稳定性,改善加工工件表面质量。
1 进给速度优化方法总体流程
针对五轴侧铣加工的特点,通过控制有效刀轴扫掠面积率改善机床切削加工过程中的不稳定状态,具体控制方法如图1所示。提取原始五轴数控加工程序的刀位点参数、刀轴参数和进给速度参数,建立以刀轨为引导线的直纹面来描述该段数控程序的刀轴运动状态。利用给定的初始材料去除率计算优化后的面积去除率,通过保持稳定的面积去除率完成五轴侧铣加工的进给速度优化。
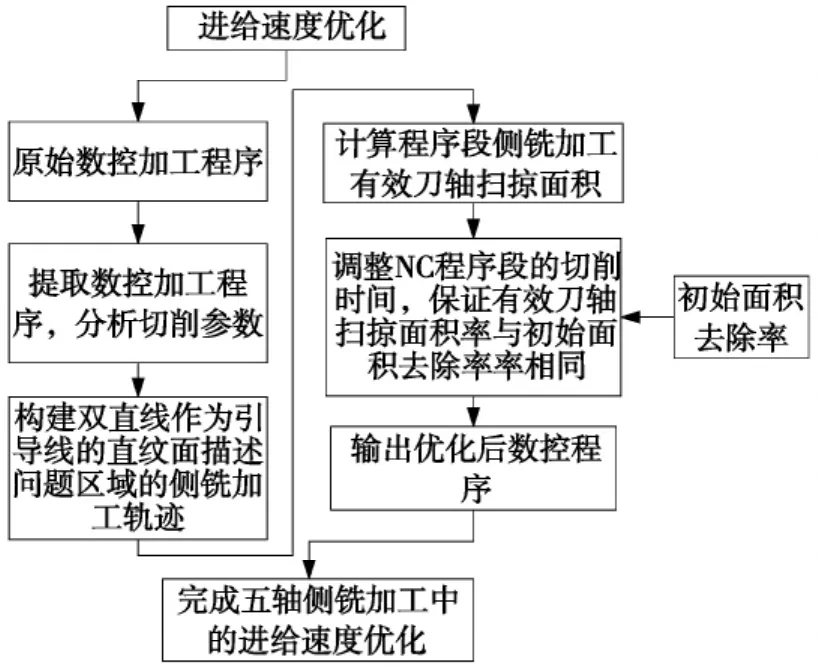
图1 五轴侧铣加工进给速度优化流程图
2 五轴侧铣加工有效刀轴扫掠面描述方法
五轴数控侧铣加工中,CAM系统通常将刀位点轨迹离散成许多微小直线段,用G01指令进行加工轨迹控制。五轴侧铣加工刀轨示意图如图2所示,在机床坐标系下,设刀位点与其对应的上刀位点的高度差(即切削深度在Z向的分量)为apz,上刀位点与刀位点的距离为D。

图2 五轴侧铣加工刀轨示意图
刀轴在执行每个G01数控指令时,其与工件接触扫掠面可近似看作由刀位点轨迹作为引导线所构成的直纹面,如图3所示。图中Pi-1和Pi为刀位点,Qi-1和Qi为对应的上刀位点。设Pi-1点处的数控程序坐标为(xP(i-1),yP(i-1)zP(i-1),AP(i-1)BP(i-1)),Pi点处的数控程序坐标为(xP(i)yP(i)zP(i)AP(i)BP(i))。

图3 直纹面模型
设H为直纹面上任意一点,P为H点所在母线的下端点,Q为H点所在母线上端点,其中:
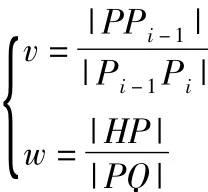
则该直纹面的参数方程可表示为:

3 刀轴与工件接触扫掠面积的计算
3.1 上刀位点求解
上刀位点可以由刀位点坐标和刀轴姿态求得。以FXYZBA机床为例,设该结构类型中刀轴绕Y轴的旋转变换矩阵为MRY(BP(i)),刀轴绕X轴的旋转变换矩阵为MRX(AP(i))。根据物体的运动变换原理可知:


则刀轴的方向矢量为[11]:

上刀位点与刀位点距离D可表示为:


3.2 刀轴与工件接触扫掠面积的求解
设第i段数控程序刀具与工件接触扫掠直纹面面积为si,该直纹面上与(v,w)参数平面内的元素dvdw对应的面积元为|r'v(v,w)×r'w(v,w)|dvdw,可应用二重积分的方法计算该直纹面面积:

4 数控程序段进给速度优化
4.1 数控程序段执行时间的求解
根据SIEMENS840D数控系统定义,当G90和G94指令有效时,第i段G01数控程序的执行时间为:
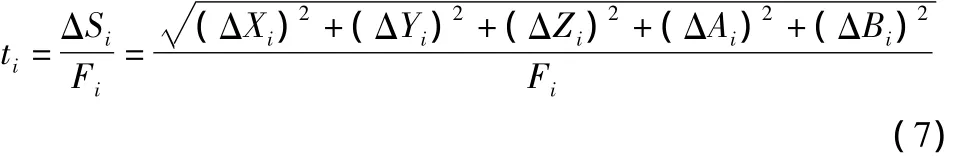
其中 ΔSi为程序段的当量位移,ΔXi、ΔYi、ΔZi、ΔAi、ΔBi为机床坐标系下数控程序段各坐标轴的运动增量[11]。

式中L是刀尖点到A轴回转中心的距离。
4.2 数控程序段进给速度的调整计算
在五轴侧铣精加工中,由于刀轴的径向切深一般为稳定值,设侧铣加工数控程序的刀具径向切深为ae,预定初始材料去除率为Q,则可得有效刀轴扫掠面积率S'的值为:

则数控程序段优化后的进给速度Fi的求解式可由公式(7)推导得:

5 进给速度优化对比试验
将图4所示筋板测试件在竖直方向(即机床坐标系下Z轴方向)分为三层进行切削加工试验,用原始数控加工程序加工第一层和第三层,用优化后的数控加工程序加工第二层。试验中使用的机床为某国产XFYZBA结构的五轴数控机床。刀具采用半径为10mm的环形立铣刀,倒角r=3mm。工件为具有一定五轴侧铣加工工艺代表性的筋板测试件(如图4所示),其毛坯尺寸为400mm×300mm×75mm。

表1 试验参数对比表

图4 筋板测试件
数控程序优化前后面积去除率如图5所示。从图中可以看出优化后面积去除率保持恒定。加工中刀具径向切深稳定为3.5mm,则优化后的材料去除率也基本稳定。
由于整个筋板测试件较大,所以截取切削加工实验结果中一部分进行显示。截取图4中一部分显示结果如图6所示。从中可以看出优化后的数控程序加工工件表面质量明显好于原始数控加工程序加工工件表面,表明了本文所述方法的有效性。
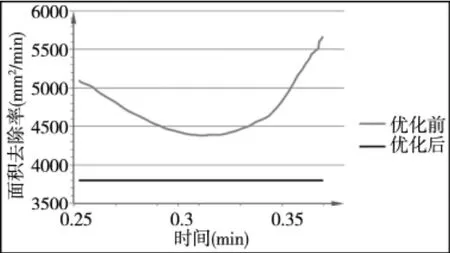
图5 优化前后面积去除率

图6 切削加工验证试验结果图
6 结论
本文针对五轴数控侧铣精加工工艺,提出以直纹面模型描述刀轴运行轨迹,以有效刀轴扫掠面积率替代面积去除率。通过积分的方法计算每一数控段中有效刀轴扫掠面积,给定初始面积去除率,调整每一数控程序段的进给速度,使其面积去除率保持稳定,并与给定的初始面积去除率相同。从而提高加工过程中的稳定性,提高加工工件表面质量。最后通过一系列的加工对比试验,验证了该方法的有效性。
[1]W P Wang.Solid Modeling for Optimization Metal Removal of Three-dimensional NC End Milling[J].Journal of Manufacturing Systems.1988,7(1):5765.
[2]K Yamazaki,N Kojima,C Sakamoto,et al.Real-time Model Reference Adaptive Control of 3D Sculptured Surface Machining[J].Annals of the CIRP,1991,40(1):479482.
[3]Z Z Li,M Zheng,L Zheng,et al.A Solid Model-Based Milling Process Simulation and Optimization System Integrated with CAD/CAM[J].Journal of Materials Processing Technology.2003,138:513 -517.
[4]Seok-Hyung Bae,Keyhoon Ko,Bo H Kim,et al.Automatic federate adjustment for pocket maching[J].Computer-Aided Design,2003,35:383 -393.
[5]Guzel B U,Lazoglu I.Increasing Productivity in Sculpture Surface Machining Via off Line Piecewise Variable Feed-rate Scheduling Based on the Force System Model[J].International Journal of Machine Tools & Manufacture,2004,44:21 -28.
[6]彭海涛,雷毅,周丹.基于铣削力仿真模型的进给速率优化方法[J].中国机械工程,2005,16(18):1607-1609.
[7]翟玉山,杨旭静.一种面向进给速度优化的数控编程后置处理开发[J].机械制造,2007,45(6):45-47.
[8]田华利.模具型腔数控铣削刀具组合与走刀方式优选[D].济南:山东大学,2006.
[9]陈志同,张保国.面向单元切削过程的切削参数优化模型[J].机械工程学报,2009,45(5):230-243.
[10]陈婷婷.基于重型机床大型零件铣削加工性能及参数优化的研究[D].苏州:苏州大学,2011.
[11]周济,周艳红.数控加工技术[M].北京:国防工业出版社,2002.

