基于逆动力学分析的上下料机器人关键零部件选型
崔敏其,吴少彬
(1.华南理工大学广州学院工程研究院,广州 510800;2.香港中文大学机械与自动化工程学系,香港)
0 引言
在上下料机器人的设计过程中,关键零部件(如电机、减速机、丝杠)的选型是至关重要的设计步骤。关键零部件选型的成功与否决定着机器人的性能能否满足设计要求。
本文运用机器人的逆动力学方法来完成机器人关键零部件的选型分析。具体是:使用Newton-Euler迭代算法建立机器人的动力学模型,使用数学软件Mathematica建立机器人逆动力学仿真系统,通过逆动力学系统进行仿真分析,获得关键动力学参数。最后根据关键参数进行选型。
1 动力学建模
1.1 正运动学模型
在动力学建模前,首先需要建立机器人的正运动学模型。如图1所示,定义各连杆坐标以及各连杆参数。使用 Denavit-Hartenberg参数法建立SCARA机器人的运动学模型。其中SCARA机器人的Denavit-Hartenberg参数如表1所示。
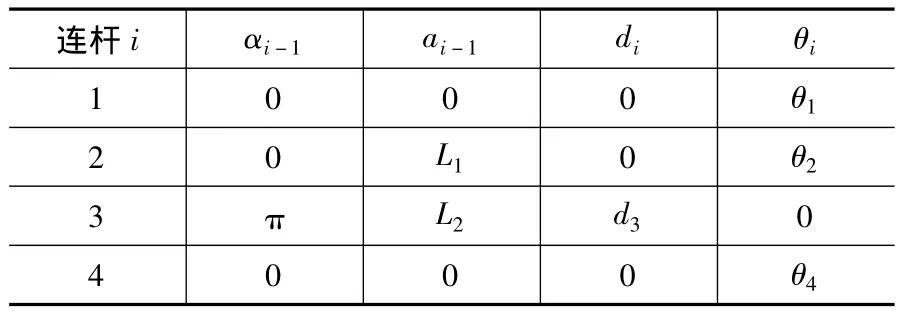
表1 Denavit-Hartenberg连杆参数表
表中 αi-1为连杆转角,ai-1为连杆长度,di为连杆偏距,θi为关节角。由连杆变换矩阵公式和变换传递式可得,机器末端({4}原点)到基坐标系的齐次变换矩阵:

通过齐次变换矩阵04T,即可在基坐标系下将SCARA机器人末端的位姿与各关节参数之间的运动学关系表达出来。至此,SCARA机器人的正运动学模型建立完毕。
1.2 逆动力学模型
使用 Newton-Euler迭代动力学算法,建立SCARA机器人的动力学模型(该算法是由 Luh、Walker以及Paul于1980年提出,见文献[1])。算法建立的依据是单连杆(如图2所示)的力的平衡和力矩的平衡。
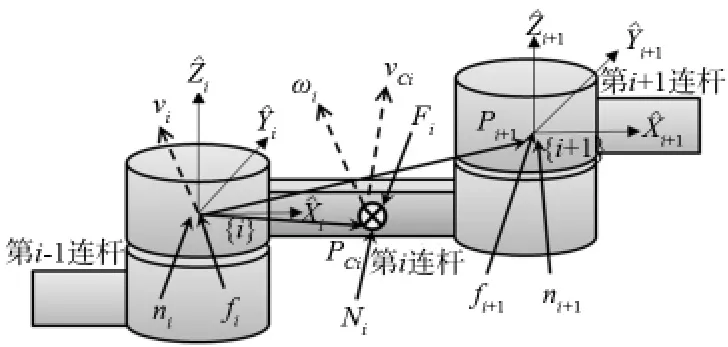
图2 单连杆速度、角速度及受力示意图
定义算法需要使用到的变量符号:为连杆i的惯性张量在其质心坐标系上的表示,iPci为连杆i的质心的矢径在连杆i坐标系上的表示,iPi+1为连杆i+1坐标系的原点矢径在连杆i坐标系上的表示。
进行外推迭代,即从i=0到i=3(从连杆1到连杆4)进行迭代运算,通过下式分别求出各连杆的角速度、角加速度、线加速度、质心线加速度、惯性力、惯性力矩。
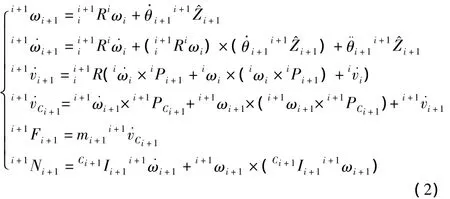
进行内推迭代,即从i=4到i=1(从连杆4到连杆1)进行迭代运算,通过下式分别求出各相邻连杆间的相互作用力ifi、作用力矩ini以及各关节力矩τi。
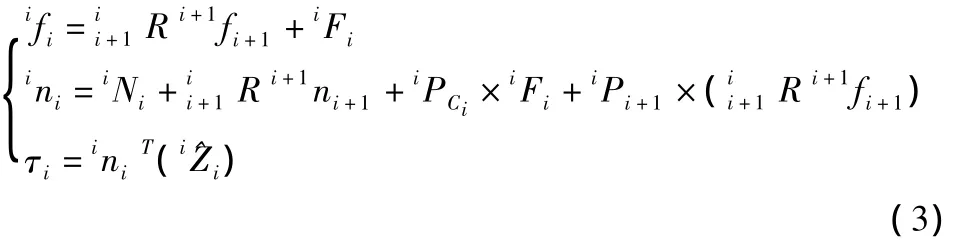
外推内推迭代是运算量很大的矩阵符号运算,由于计算十分复杂冗长,因本文版面的限制不能列举由动力学模型推导出的详细过程及结果。通过Mathematica进行符号运算,我们可以较为方便地计算出各连杆运动学和动力学参数关于连杆参数的函数表达式,从而得出SCARA机器人的动力学模型:

本文利用机器人的逆动力学分析来进行关键零部件的选型。所谓逆动力学问题,指的是给定机器人运动的角位移、角速度、角加速度,求解满足运动所需的各关节的驱动力矩(力)。同时,在逆动力学求解过程中,通过部分中间结果,可以计算相关的关节功率Pi、转速Ri以及关节倾覆力偶矩Mi(关节力矩在水平面上的分量的大小)。它们的计算公式分别为:

以上所述数学模型为图3所示的SCARA Inverse Dynamics模型。

图3 SCARA机器人逆动力学仿真系统
1.3 获取选型参数
获得逆动力学模型后,我们便可以计算各关节轴的实时所需的扭矩、关节转速、关节功率、关节倾覆力偶矩等。在关键零部件选型分析中,我们更关心的是,在机器人运动过程中,各关节轴所需的扭矩的最大值、关节转速最大值、关节功率最大值、关节倾覆力偶矩的最大值。此时,我们需要设计一个最大值捕获器(如图3),用于获取上述各量在机器人运动期间出现的最大值。

式中Maximize[]为求最大值函数(可以使用Mathematica计算)。关节轴的最大扭矩τimax、最大转速Rimax以及最大功率Pimax是电机和减速机选型的最重要依据。关节倾覆力偶矩Mi则是关节轴承选型的重要依据。
2 选型分析
通过上下料机器人设计实例来进行动力学建模及选型分析。
2.1 机器人基本参数
用于上下料的SCARA型机器人,大小臂长度分别为250mm、350mm。物料的额定质量为6.11kg,末端负载有33.57mm的偏心距离,搬运节拍(周期)为6s,搬运距离为1050mm。该机器人各关节的运动范围和运动时间如表2所示。具体的连杆参数如表4所示。连杆一、二、三、四的质量分别为:4.09kg、9.88kg、0.66kg和8.88kg。表2表中所述的“运动时间”指的是SCARA机器人带载情况下,各关节轴从极限位置1到极限位置2所需的运动时间。

表2 各关节轴部分设计指标
2.2 动力学仿真与分析
设定动力学仿真参数。根据各关节轴设计指标,初定SCARA机器人1、2、4关节按照余弦曲线运动,关节3保持静止(如表3所示),分析在这种情况下的机器人各关节轴所需的扭矩的最大值、关节转速最大值、关节功率最大值。

表3 轨迹发生器
上述最大值(选型量)的计算需要使用Mathematica或Matlab,建立如图3所示的SCARA机器人逆动力学仿真系统进行仿真分析,方可求解。

图4 逆动力学仿真结果
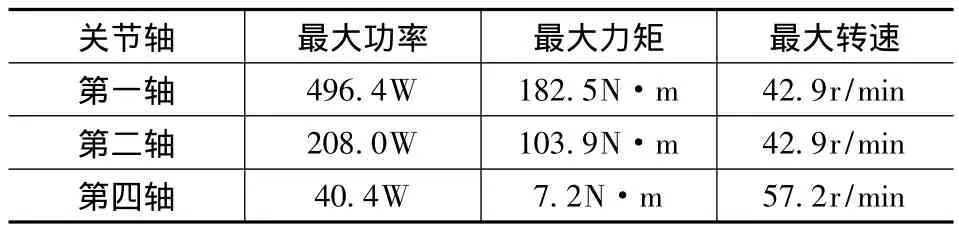
表4 逆动力学仿真结果
本文是通过Mathematica8.0编写逆动力学仿真程序,部分仿真结果如图4和表4所示。图4所示的τ3曲线,单位为N。通过图4、表4数据以及惯量匹配分析(本文略),上下料SCARA机器人一、二、四轴电机及减速机选型结果如表5所示,机器人部分性能参数如表6所示。

表5 电机、减速机选型结果
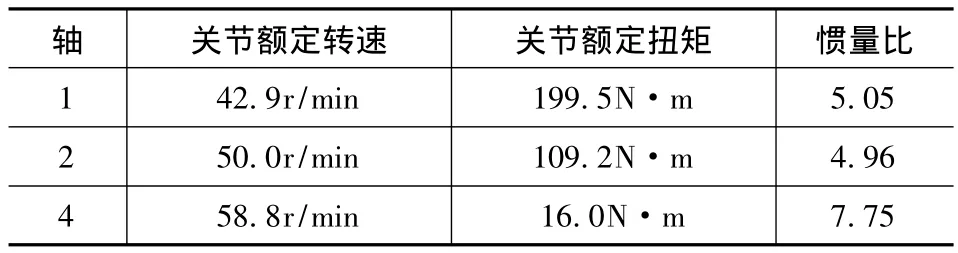
表6 机器人部分性能参数
3 结论
本文运用机器人的逆动力学方法来完成机器人关键零部件的选型分析。方法具体步骤是:使用DH参数法建立机器人的运动学模型,使用Newton-Euler迭代算法建立机器人的动力学模型,使用数学软件Mathematica建立机器人逆动力学仿真系统,计算机器人在运动过程中各关节的功率、扭矩、转速及相邻连杆间的相互作用力。逆动力学模型建立后,可以对机器人在额定工况、极端工况下的运动情况进行动力学仿真,得出相应情况下的选型量,以此作为依据,进行机器人的关键零部件选型,同时为其它类型机器人选型提供了参考。
[1]J.Y.S.Luh,M.Walker and R.Paul,On-line computational scheme for mechanical manipulators[J].J.Dyn.Sys.Meas.& Contr.,1980,102:69 -76.
[2]J.J.Craig,Introduction to Robotics:Mechanics and Control[M].3rd ed.Upper Saddle River,N.J.:Pearson/Prentice Hall,2005:62 -89.
[3]S.M.Megahed,Principles of Robot Modelling and Simulation[M].Chichester;New York:J.Wiley,1993:186-191.
[4]NaoyukiIshibashi,YutakaMaeda.Learning of inverse-dynamics for SCARA robot[C]SICE Annual Conference(SICE),IEEE Conference on 2011:1300-1303.
[5]F.L.Lewis,C.T.Abdallah and D.M.Dawson,Control of Robot Manipulators[M].New York:Macmillan Pub.Co.,1993:64 -90.
[6]H.Josephs and R.L.Huston,Dynamics of Mechanical Systems[M].Boca Raton:CRC Press,2002:415 -418.
[7]S.Arimoto,Control Theory of Non-Linear Mechanical Systems:A Passivity-Based and Circuit-Theoretic Approach[M].Oxford:Clarendon Press,1996.
[8]S.Niku,Introduction to Robotics[M].Wiley:2011:147 -169.
[9]Ferdinand P.Beer,E.Russell Johnston,David F.Mazurek ect.,Vector Mechanics for Engineers:Statics and Dynamics[M].9nd ed.Boston:McGraw-Hill Higher Education,2011:914-998.
[10]谢存禧,张铁.机器人技术及应用[M].北京:机械工业出版社,2005.

