一种减缩CFD非定常分析计算量的方法

杨 鸣，赵世平，王汉平，张煜冰，王邵助

(1.北京理工大学 宇航学院，北京 100081;2.北京机电工程研究所 11室，北京 1000781)

非定常气动力精确计算是飞行器动气弹和气动伺服动力学问题得到准确分析前提［1-8］，也是了解飞行器操纵性、机动性和稳定性等飞行品质的关键。

针对非定常气动力计算，传统上往往引入准定常假设，假定在任何非定常运动瞬间飞行器气动特性都与同一飞行器以等速度进行平移或转动时所显现的气动特性一致，这实际上忽略了运动和频率的依赖关系［9］。准定常假设在工程上简单易用，但用于颤振和动响应分析时精度不足，在理论上也是站不住脚的。对于非定常运动的正确处理方式，是借助CFD分析中动网格技术建立流场中的动边界模型，让物体在流场中以真实的形态“运动”，这种指导思想下建立的模型在理论上才是完备的，在工程实践上也具有更高精度。要让运动物体在计算域中“运动”起来，需要预先构造足够大且覆盖物体运动空间的网格计算区域。但是，以飞行器为代表的航行体运动速度快，达到每秒数百米乃至上千米的数量级，即使仅仅只分析飞行器数秒时间范围内的运动流场，在其主要运动方向上也必须构造成百上千，甚至上万米的运动区域，如果还要进一步考虑飞行器的三维几何效应，那么其所需计算资源将是现有绝大多数计算机都无法提供的。减缩计算量将是非定常运动问题分析一个重要课题。

本文抓住飞行器运动流场特征，即在远离飞行器的流场区域应为未扰动远场区域，提出在计算时只够造部分计算域，对飞行器已经经过远离且恢复为远场条件的区域实时删除，同时又对飞行器将要经过的远场区域实时扩展以保证计算进行。这种处理方式使得计算域始终之只限制在飞行器周围，无需构建起整个计算域，从而大大减少了计算量且对计算精度基本没有影响。

1 方法原理

1.1 域动分层技术

对六面体或者楔形网格区域，可以使用运动分层技术来生成或者删除边界网格。当网格边界和邻近一层网格有相对运动时，若紧邻边界网格高度增长到一定高度，就将其划分为2个网格层;反之，当网格层高度降低到一定程度时，就将紧邻边界的2层网格合并为一层网格以杜绝负体积网格的出现。

网格层扩大准则:

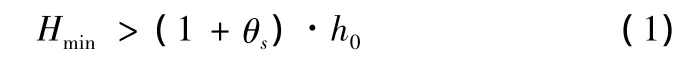
式(1)中:Hmin为网格最小高度;h0为理想高度;θs为分割因子，在满足该条件前提下，就对网格单元执行分割操作。

网格层缩减准则:

式中:θc为合并因子，在满足这个条件时，就将该层网格与外面一层网格合并［10］。

1.2 非定常流场特征与计算方案

飞行器在自由空间中运动，其流场呈现出如下特征:在靠近动壁面区域，速度场、压力场和温度场变化剧烈，呈现高度非线性、非定常特点，是流场计算主要关心区域［11-13］。而在远离飞行器特征长度以外的区域(一般可取为特征长度20～30倍)，物理场变化微小，属于平稳的未扰动流场区域，其流动状态简单且可以直接给定，其并非计算分析关心区域［14-15］。由于这个特点，如果将飞行器所有运动区域都预先构造计算网格，实际上就等于引入了多余的无关计算。而未扰动区域网格数占整个计算域网格数百分比很大，往往将达到30%～50%，如果能够在计算时忽略掉这部分网格，那将大大缩减计算规模，且对计算结果影响极小。

利用这个特点，本文将飞行器流场计算分割为若干个阶段，在计算一开始只构造一部分计算网格，远离运动物体区域一律划分为结构化网格。当运动物体在计算域中运动一段时间以后，在物体运动反方向上利用前述域动分层技术缩减网格，而在沿着物体运动方向则相应扩展网格以保证计算得以继续。通过这种处理方式，计算量被大大减少，这对于必须利用动网格技术的CFD计算具有重要意义。

2 算例

2.1 基本模型的选取

以二维NACA0006翼型的非定常流场计算作为示例将传统方法和新方法进行对比。湍流模型使用在空气动力学计算中常用的Spalart-Allmaras一方程模型，该模型将湍动黏度μt表示为湍动能k的函数，其输运方程为

流场边界为远场条件，由于本算例假设飞行器是以一定速度在相对惯性系静止流场中运动，故来流马赫数Ma=0，压力为50662 Pa，温度216.6 T。其中动区域和静区域设置如图1，①、②、③、④、⑤、⑥分别为动区域和静区域的边界，⑤、⑥在计算过程中为静止边界。

图1 动区域和静区域示意图

机翼运动规律为沿x负方向以10 m/s2加速度从300 m/s速度在2 s时间内加速运动到320 m/s，为了减少初始速度对计算结果的影响，前0.2 s以300 m/s速度匀速运动，因此实际运动时间为2.2 s。由运动公式可知，机翼实际位移为680 m。

2.2 传统计算方案网格布置

计算域尺寸如图2所示，网格为四边形结构化网格，总的网格数为501688个。

图2 计算域大小示意图

2.3 新的计算方案网格布置

初始计算域大小如图3所示，机翼每前进100 m，就对网格区域进行一次“减缩-扩展”操作。进行这一操作时，应当将动区域和静区域设置为可变形域，而将①、②、③、④、⑤、⑥6组边界设置为刚体运动沿x负方向运动100 m，这样既使得了计算域规模基本不变，又防止了内部区域随同“减缩-扩展”操作时一起运动，保证不因为该操作破坏机翼附近区域正常的流场形态。整个计算域网格数为281796个，较之传统计算方案减少了43.83%。

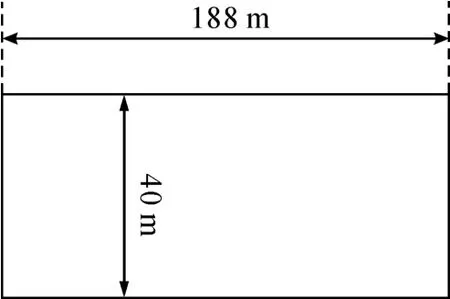
图3 计算域大小示意图

3 计算结果

在2台配置相同计算机上计算，2组模型时间步长设置一致，迭代情况也大体一致。传统计算方案计算时间为156 h左右，新方案计算加上“减缩-扩展”操作所耗费时间，一共耗时110 h左右，减少了30%左右的计算时间。

图4～图6为2种计算方案在计算终了时刻各个物理场对比等值线图。可以看出，2种计算方案差异很小。

图4 压力等值线图对比

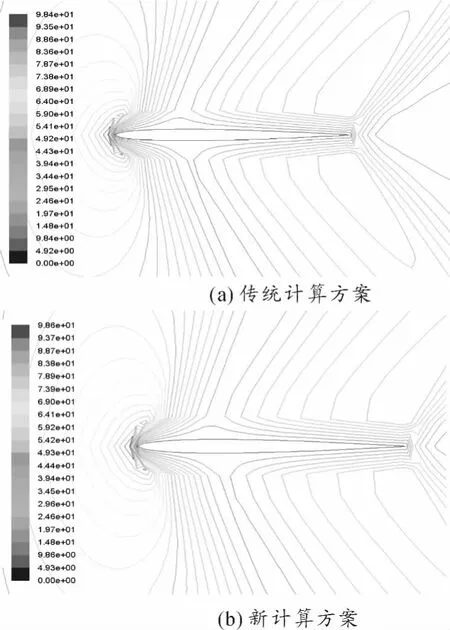
图5 速度等值线图对比

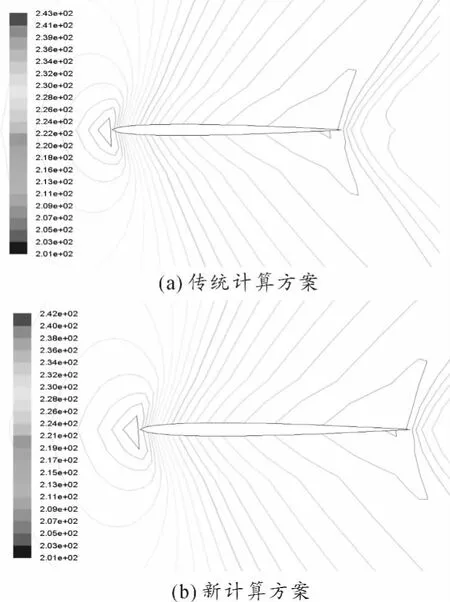
图6 温度等值线图对比

图7为新计算方案得到的阻力与传统计算方案之间的相对误差随时间变化曲线，图8则为升力的相对误差随时间变化曲线。

图7 阻力相对误差

图8 升力相对误差

由相对误差图可以看出，阻力计算误差比升力误差要小一个数量级，造成升力误差相对较大的原因在于计算域纵向尺寸取的还不够大，从而放大了对网格进行“压缩-扩展”操作以后造成的误差，对此可以采取适当放宽计算域纵向尺寸办法来加以克服。

4 结束语

结合飞行器非定常运动流场的特点，采用新的计算方案可以减少计算量，如果再采取其他相关措施，例如网格控制等手段，计算量的减缩量是很可观的。和传统计算方式相比，新的计算方案并不会降低精度。新的计算方法操作简单，具备工程可实施性和易用性，对非定常流动问题计算具有指导意义。

［1］陈桂彬，邹丛青，杨超.气动弹性设计基础［M］.北京：北京航空航天大学出版社，2007：64.

［2］Friedmann P P.Hypersonic aerothermoelastic characteristics of a finned missle［J］.Journal of Space craft，1979，16(3)：187-190.

［3］Lighthill M J.Oscillating airfoils at high mach numbers［J］.Journal of the Aeronautical Sciences，1953，20(6)：402-406.

［4］McNamara J J，Thuruthimattam B J，Friedmann P P，et al.Hypersonic aerothmoelastic studies for reusable launch vehicles［R］.AIAA-2004-1590，2004.

［5］Lind R.Linear parameter-varying modeling and control of structural dynamics with aerothermoelastic effects［R］.AIAA-1999-1393，1999.

［6］杨超，许贇，谢长川.高超声速飞行器气动弹性力学研究综述［J］.航空学报，2010，31(1)：1-11.

［7］陆洋，王浩文，高正.电控旋翼气弹动力学建模研究［J］.航空动力学报，2006，21(6)：1021-1026.

［8］康浩，高正.舰面直升机旋翼瞬态气弹响应分析［J］.航空动力学报，2000，15(1)：67-70.

［9］J.R.赖特，J.E.库珀.飞进气动弹性力学及载荷导论［M］.姚一龙，译.上海：上海交通大学出版社，2010：146.

［10］吴光中，宋婷婷，张毅.FLUENT基础入门与案例精通［M］.北京：电子工业出版社，2012：329-330.

［11］伍贻兆，田书玲，夏健.基于非结构动网格的非定常流数值模拟方法［J］.航空学报，2011，32(1)：15-26.

［12］许和勇，叶正寅，王刚，等.基于非结构运动对接网格的旋翼前飞流场数值模拟［J］.空气动力学报，2007，25(3)：325-328.

［13］乔阳，刘勇，徐敏，等.基于多块对接网格的多侧喷流瞬态干扰特性研究［J］.固体火箭技术，2007，30(21)：552-554.

［14］宋琦，杨树兴，徐勇，等.滚转状态下卷弧翼火箭弹气动特性的数值模拟［J］.固体火箭技术，2008，31(6)：98-101.

［15］倪同兵，招启军，赵国庆，等.应用多块对接结构网格方法的直升机涵道尾桨气动特性［J］.航空动力学报，2011，29(6)：688-695.