多约束条件下的复杂纵断面设计及评价研究

余豫新

（上海市政交通设计研究院有限公司，上海 200030）

多约束条件下的复杂纵断面设计及评价研究

余豫新

（上海市政交通设计研究院有限公司，上海 200030）

系统分析了纵断面设计的关键因素，并且结合某工程实例，为多约束条件的复杂纵断面设计提供了思路和方法；通过研究评价指标与评价方法的对应关系，提出了基于DEA方法的纵断面方案定量评价方法，解决了以往定性选择纵断面方案时易产生的主观性、片面性的问题。

城市道路；纵断面；DEA方法；评价指标

0 引 言

城市道路是市政建设最重要的基础设施之一，伴随着国家整体实力的稳步提升，中国的城市道路建设已经取得了巨大的成就，城市道路设计的理论、方法等也逐步完善，形成了成套的规范及指南。

纵断面设计是道路设计中非常重要的一个环节，需要考虑的因素众多，灵活性大，技巧性强，因此也是整个设计方案成败与否的关键。而且，约束条件较多的纵断面设计往往出现多方案比选的情况，定性的评价存在一定的主观性和片面性，较难准确比选出最佳方案。因此，本文结合上海某道路纵断面方案比选的实例，系统分析研究了纵断面设计的关键因素以及基于DEA理论的定量评价方法。

1 纵断面设计的约束条件

城市道路纵断面设计是一个复杂、多元化的综合任务，在设计时需权衡协调各种因素，最终确定最佳方案。结合纵断面相关设计原则［1－3］，经过深入系统的分析，得出了纵断面设计的约束条件。

（1）满足相应设计速度的纵断面线形技术要求。相应设计速度下的纵断面线形技术标准是纵断面设计的基础依据。《城市道路工程设计规范》（CJ J37—2012）中明确规定了纵断面设计的坡度、坡长以及竖曲线半径等指标，为科学安全的纵断面设计提供了保障。

（2）满足桥梁、地道等构筑物的净空要求。桥梁的梁底控制标高受河道正常水位以及通航等级两方面的约束，是道路纵断面必须满足的控制点；地道的最小净高是扣除地道结构厚度以及铺装层厚度之后而满足机动车辆通行的最小高度；与设计工程立体相交的其余构筑物也应满足相应的标高要求。

（3）满足与规划及现状道路交叉口标高良好衔接的要求［4］。平面交叉口需与规划及现状道路标高接顺，以满足整个区域的竖向规划，同时尽量避免已建工程的翻挖重建。

（4）满足各种市政管线敷设的要求。市政道路下面均敷设有雨水、污水、通讯、电力等管线，因此纵断面设计还需考虑管线埋设的最小覆土厚度。

（5）满足道路及周边地块排水要求。道路纵向排水主要依靠纵坡，城市道路中不小于0.3%的纵坡即认为满足纵向排水要求；道路标高一般略低于沿线地块标高，以满足地块排水要求。

（6）满足路基标高要求，保证路基处于稳定工作状态。路基是道路主要的承重层，因此保证路基处于稳定工作状态直接关系到整个工程的安全性与耐久性。针对不良地质路段要严格控制地基处理范围及深度，纵断面设计要结合不良地质情况及地下水位确定控制标高。

（7）结合地形，尽量减小土方数量。土方数量是控制工程造价的重要因素，纵断面设计线应顺应现状地面线的趋势，并且尽量靠近地面线，以有效减少填挖方量，节省土源，降低工程造价。

（8）满足机动车行驶舒适性及节省燃油的要求。纵断面频繁的起伏变化会影响机动车的行驶舒适性，驾驶员在启动、制动间来回切换，容易造成驾驶疲劳，不利于行车安全，同时增大油耗，对机动车磨损较大，缩短了车辆使用寿命。

（9）尽量体现道路纵向线形的美观。纵向线形的美观主要体现在较好地融合了沿线地形地貌，起伏平缓，错落有致［5］。例如桥梁两侧坡度的对称布设就体现出了对称之美。

一个优秀的纵断面设计方案是在满足以上各点的情况下，优中选优而确定的。但是往往会出现顾此失彼的情况，这就需要设计人员仔细分析，斟酌取舍，在必须满足前五项的条件下，结合工程实际情况，选择取舍原则，确实无法满足的约束条件需采取相应的路基加固或增大竖曲线半径等措施补偿。

2 城市道路纵断面设计方案研究比选

本工程是上海市某高科技园区的一条城市道路，规划为城市支路，纵断面约束条件较多，设计复杂。工程起、终点分别与已建及在建道路平面相交，一条六级航道通航要求的河流横穿该工程，高差较大，且距离较近，为科学合理的纵断面设计带来了极大的困难。

2.1 设计约束条件

（1）设计速度为30km·h－1。

（2）工程终点为在建道路A，规划为城市次干路，现状标高约为4.8m。

（3）工程终点向南约100m为规划河流B，河宽为48m，满足六级航道要求的桥梁控制标高为10.96m；根据周围已建桥梁标高以及与航务部门沟通，桥梁控制标高最低可降低至9.46m。

（4）河流B向南约250m为规划河流C，河宽为30m，控制标高为6.76m。

（5）地块规划标高约为5.0m。

（7）地块规划的景观要求较高。

2.2 设计方案研究

纵断面设计时综合考虑以上各约束条件，并且结合车辆行驶安全性、舒适性，线形的协调美观、桥梁结构的科学合理性以及工程的经济性等因素，根据航务部门提供的规划通航净高（10.96m）要求提出了4个纵断面方案，根据协调后可能降低的净高（9.46m）要求提出了2个方案，进行方案综合比选，如图1～6所示。

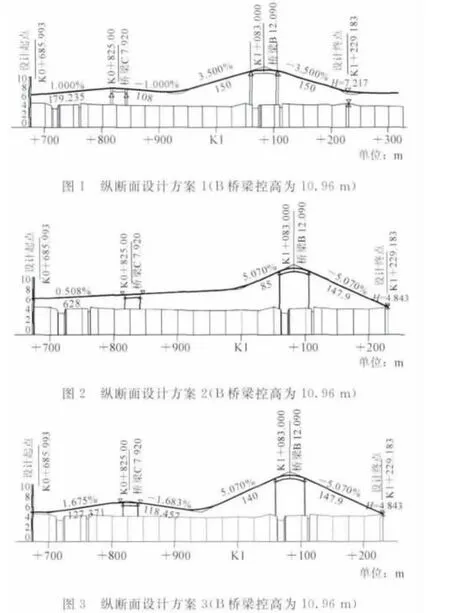
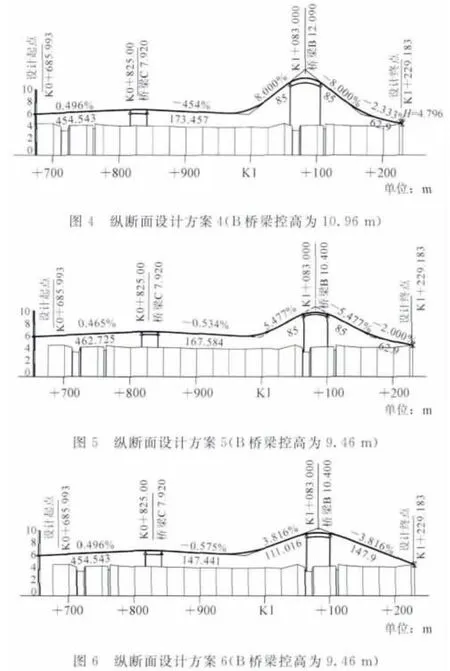
方案1是惟一一个满足非机动车骑行的方案，即3.5%纵坡坡长小于150m。优点是：非机动车可骑行；线形较为平缓，可确保行驶舒适性和安全性。缺点是：不能够与在建的A道路标高接顺，路口需抬高约2.5m；整条道路填方量较大。

方案2的优点是：最大纵坡约5%，未取至极限值；整体线形较为顺畅，避免了线形的反复起伏。缺点是：非机动车需推行；与A道路交叉口处坡度较大，不利于停车及行车安全；填挖方量较大。

方案3和方案2的主要差别在于对桥梁C纵坡的处理，方案3桥梁C两侧纵坡对称布设，有利于桥梁景观设计。优点是：最大纵坡约5%，未取至极限值；两座桥梁段纵坡均对称布设，较为美观；填挖方量较小。缺点是：非机动车需推行；与A道路交叉口处坡度较大，不利于停车及行车安全；道路纵断面频繁起伏变化，短距离内需要加速、制动，不能满足驾驶舒适性。

方案4采用30km·h－1设计速度下的极限最大纵坡，从而避免了交叉口处的大纵坡。优点是：与A道路交叉口处纵坡相对较缓，有利于交叉口的停车及行车安全，避免了由于纵坡过大而导致驾驶员冲过交叉口；桥梁段纵坡对称布设，较为美观。缺点是：非机动车需推行；桥梁段采用最大纵坡极限值；接近路口处坡长不满足30km·h－1设计速度下最小坡长85m的标准。

方案5和方案6是基于桥梁控制标高为9.46m的情况而设计的，但是该标高还需根据沿线竖向规划以及已经在建桥梁的标高进一步研究确定，是一种比较合理的控制标高。

1990年中国与印尼恢复外交关系后，印尼政府对华人的政策开始变得宽松。由于1966年后印尼开始有很多来自台湾的商业投资，1990年印尼政府同意为在印尼的台湾子女建立台北学校，教学材料可以从台湾引进。“1994年政府开始准许国民学习华语，也准许民间开办华语补习班”。[9]1994年6月11日“印尼内政部政治司签署文件准许两所指定的大学，即印尼大学和达尔玛·勃尔沙达大学(Universitas Darma Persada)的汉语系开设汉语必修课”[10]，这说明印尼政府开始对华语作为外语的教学放宽限制。1998年5月印尼发生排华事件，苏哈托总统同月宣布下台。

方案5的优点是：整体纵坡较为平缓，行驶比较舒适；与A道路交叉口处纵坡较缓，有利于交叉口的停车及行车安全，避免了由于纵坡过大而导致驾驶员冲过交叉口；桥梁段纵坡对称布设，较为美观。缺点是：非机动车需推行；接近路口处坡长不满足30km·h－1设计速度下最小坡长85m的标准。

方案6的优点是：最大纵坡约3.82%，较为平缓；桥梁段纵坡对称布设，较为美观；填挖方较小。缺点是：非机动车需推行；与A道路交叉口处坡度较大，不利于行车安全。

2.3 综合比选

由表1可见，方案1、5、6均有1项指标不满足要求；方案2、3有2项指标不满足要求；方案4有3项不满足要求。根据表1的定性评价仅能排除方案4，其余方案的优势并不明显，但是根据经验，拟推荐方案5，在这种情况下复杂项目的纵断面方案比选缺乏准确的依据，无法通过直观的定性评价而确定。因此，需引入一种既方便快捷又能够准确区分各方案优劣的评价方法。本论文采用数据包络分析法（DEA方法）定量评价各方案的优劣，从而科学地指导设计者确定最佳纵断面设计方案［6］。

3 纵断面方案评价

3.1 DEA方法模型

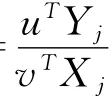
表1 纵断面方案比选分析

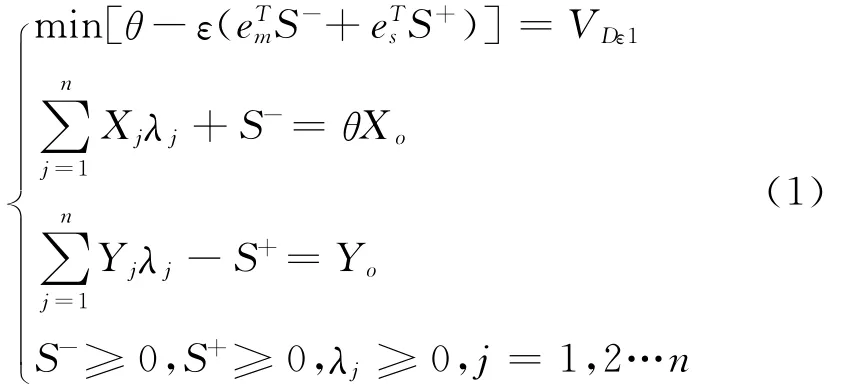
式中：ε为非阿基米德无穷小量，是一个大于零而小于任何正数的数；VDε1为带有阿基米德无穷小量的线性规划最优值＝（1，1…1）∈Rm，Rm为m维实数矩阵；＝（1，1…1）∈Rs，Rs为s维实数矩阵；S－，S＋分别为输入、输出偏差变量；θ为综合有效系数。

此模型的综合有效系数θ＝1，则该评价对象为弱DEA有效；若在上述条件下，它的每个最优解λ＝（λ1，λ2，…λn）T，S＋，S－均有S＋＝0，S－＝0，则此评价对象为DEA有效，即为该评价对象最优。

3.2 基于DEA方法的纵断面方案比选

本次共选取6项指标作为输入、输出指标，其中输出指标为：规范符合度、与构筑物及被交道路的衔接度、线形美观性；输入指标为：燃油消耗率、事故率、填方率。共有6个被评价方案，用xij表示第j个方案的输入指标值，yrj表示第j个方案的第r个输出指标值（j＝1，2，…，6；r＝1，2，3）。对输入指标引入非负偏差变量≥0，3种输出指标引入非负偏差变量，且均不小于0，记S－＝（）T，S＋＝（，）T，确定第j个方案的评价指数。其具体数据见表2及表3，表中θ为综合有效系数；为输入指标的非负偏差变量，、、分别为3个输出指标的非负偏差变量。

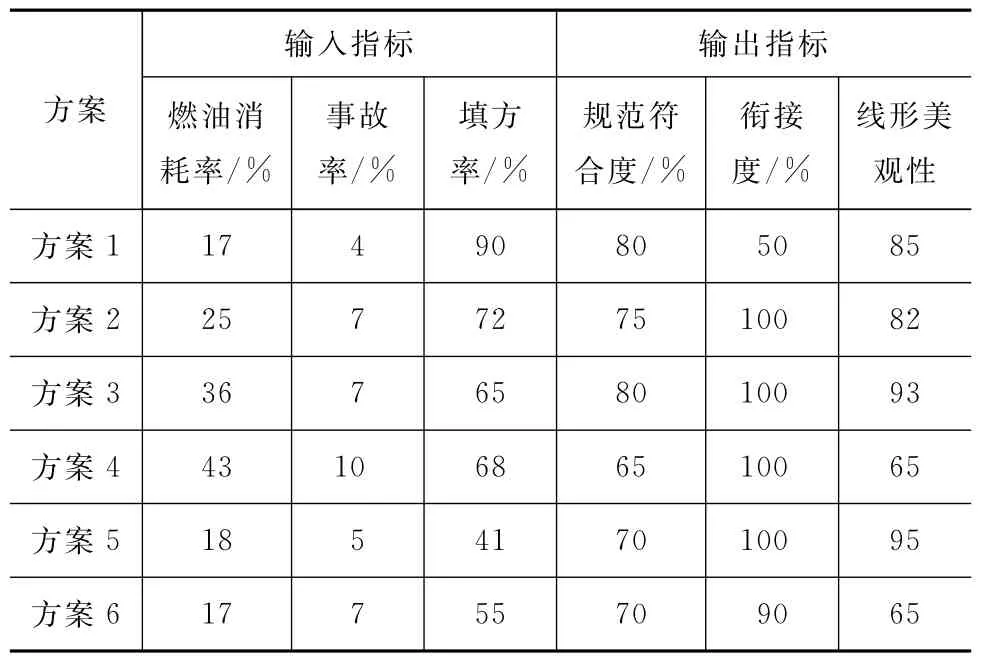
方案1 17 4 90 80 50 85方案2 25 7 72 75 100 82方案3 36 7 65 80 100 93方案4 43 10 68 65 100 65方案5 18 5 41 70 100 95方案6 17 7 55 70 90 65

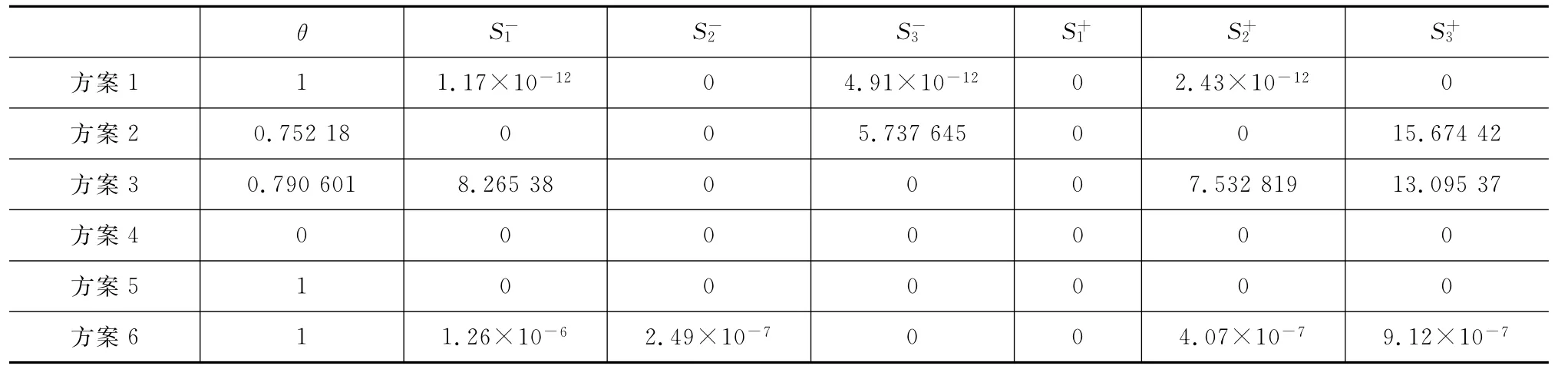
表3 计算结果

由表2计算分析可得以下结论。

（1）θ＝1，且＝＝＝＝＝＝0的评价单元为方案5，根据DEA理论，本方案为纵断面最佳方案。

（2）θ＝1，且＝＝＝＝＝≠0的评价单元为方案1和方案6，即为DEA弱有效的方案。

（3）其余的评价单元θ＜1，即这些方案非DEA有效。

基于以上结果及分析，由DEA评价而得到的最优方案为方案5，这与按照经验推荐的最优方案一致，因此基于此方法而进行的纵断面方案定量评价是可行的。

3.3 评价方法的优势

基于DEA方法的纵断面方案评价主要优势体现在以下4个方面。

（1）评价结果稳定性强，有效减少了其他评价结果易出现的离散性大、变异性强的特征。

（2）评价既不必确定各指标的权重，也不需回归分析输入、输出指标之间的函数关系，使得评价更具客观性。

（3）评价方法简单易行，便于操作，可通过excle或者matlab实现。

（4）本方法不仅适用于优选一个最佳方案的情形，同样适用于多方案按优劣排序的情况，即若规划结果出现多方案DEA有效，可仅对有效决策单元进行重构优化再评价，此时其相对差异增大，有效决策单元的优劣明显，从而实现多方案的全排序。

4 结 语

纵断面设计及比选是一项多约束条件下的复杂工程，其优劣直接影响着道路的安全性、舒适性及美观性，需要道路设计者倾注更多的时间及精力。本文通过对上海市某项目的纵断面设计方案分析及比选，系统研究了纵断面设计的约束条件，为该种类型的道路纵断面设计提供了思路及方法。与此同时，通过研究评价指标与评价方法的对应关系，提出了基于DEA方法的纵断面方案定量评价方法。

［1］牛兆霞.公路纵断面线形舒适性评价方法研究［D］.西安：长安大学，2005.

［2］魏广胜，黄治炉，何艳芳.珠江黄埔大桥纵断面设计比选论证［J］.中外公路，2009（4）：325－328.

［3］吴 林，唐 云.浅谈轻型高速公路路线纵断面主要指标的采用［J］.公路，2010（6）：119－124.

［4］韩跃杰，许金良，杨宏志，等.城市群连接7道路横断面设计研究［J］.中国公路学报，2012，25（4）：49－56.

［5］霍娅敏，陈 坚，李啸虎，等.城市区建观项目交通影响后评价模型［J］.交通运输工程学报，2012，12（1）：79－86.

［6］魏权龄.数据包络分析［M］.北京：科学出版社，2004.

［7］余豫新，王选仓，张 和，等.智能交通评价系统中DEA方法的优化［J］.山东交通学院学报.2010，1（18）：17－22.

Study on Design and Evaluation of Vertical Section Under Multi－constraint

YU Yu－xin
（Shanghai Municipal ＆ Traffic Design Institute，Shanghai 200030，China）

The key factors of the design of vertical section were analyzed systematically.Combined with a project，the thinking and method of vertical section design under multiconstraint were proposed；the quantitative evaluation method of vertical section based on DEA was proposed through studying on the relationship between index and method，so the problem of subjective and one－sidedness during selecting was solved.

urban road；vertical section；DEA method；evaluation index

U412.33

B

1000－033X（2013）11－0076－05

2013－03－22

谭忠华］