基于增加最优优先搜索多样性的研究

李伟生，代 飞

（重庆邮电大学 计算机科学与技术学院，重庆400065）

0 引 言

智能规划是寻找一个有效动作序列，将某个现实问题从一个已知的初始状态转换成满足特定条件的目标状态的过程，这种有效动作序列称为规划解。目前解决规划问题主要有3种方法：第一种是规划图方法；第二种方法是约束可满足方法；第三种方法是启发式搜索方法，用启发式函数产生规划实例的估价，用该估价来指导规划在状态空间中的搜索。在以上3种方法中，以启发式搜索的效率最好，并且可以结合其它方法。所以现今大多数的规划器都采用了启发式搜索技术，它通过将规划问题转化为状态空间上的路径来搜索规划解。规划大赛中表现较好的规划器如：Fast－Downward［1］、LAMA［2］等都采用了启发式搜索策略。尽管，最优优先是一个相对有效的启发式搜索策略。但当启发式函数对状态节点估计有误时，最优优先搜索的效率将会降低。比如启发式函数将一些无利状态节点的启发式值估计为最小，然后，最优优先算法就会先去扩展这些无利的状态节点，以至于搜索到的规划解质量不高。还有一种情况是在搜索状态节点过程中会产生一种状态节点启发式值不再减少的高原现象［3－4］，如果还是单一依赖启发式函数估计的最优状态节点进行搜索，不采用别的方法避免这种高原状态的话，会导致规划代价较大。

本文以主流的规划器LAMA［2］为研究对象。深入分析了最优优先搜索策略的优缺点，提出了一种增加状态节点选择多样性的方法，通过对不同路径执行尽量多的搜索，能够避免由于启发式函数地估计错误和高原状态而导致搜索到的规划解的最优度不高的问题。

1 相关的启发式搜索策略

随时修复 A＊ （anytime repairing A＊）［5］。它在搜索到一个规划解时，利用此次规划解的代价进行剪枝，力求得到代价更小的解。在Anytime Repairing A＊迭代搜索中，上次搜索成功后产生的节状态节点继续保留为下次使用。但在这里就存在一个问题，由于启发式函数的估计并不准确，如果不清空，当上次搜索到一个质量较差的规划解时，下次搜索规划解时会受到上次搜索时所产生的状态节点的影响，不利于改善规划质量［6］。

KBFS （K－best－first－search）［7］。KBFS是最优优先搜索和广度优先搜索［8］的结合。KBFS选择节点扩展时，先从开列表中选择K （K＞1）个最优状体节点扩展，然后才产生后继状态节点。该算法通过延迟检测后继状态节点的启发式信息，来增加搜索的多样性。参数K用于增加状态节点选择的范围，K越大，搜索中扩展的状态节点越多，就能在状态空间中搜索到不同的路径，进而选择最优路径。KBFS能够在一定程度上避免由于启发式函数估计错误而导致的高原状态和局部最优先现象。但是，如果它所选择的这K个状态节点被错误的估计为有利状态节点的话，就会导致搜索到的规划解最有度不高。可以通过增加K值来避免这种情况，但是随着K值变大，KBFS的搜索类似于广度优先搜索，无法利用启发式信息指导搜索，导致整个搜索过程效率低下。

自由走步 （random－walk）策略［9－10］。它采用了一种探测策略，在一定的搜索步长范围内，随机扩展一些状态节点，从而在一定程度上避免了单一依赖启发式函数指导搜索导致的问题，增加了选择的多样性。但是这种方法有一个问题，它会忽略已搜索到的状态空间，使得相同的状态节点在不同的路径上被重复估计。

2 BBFS （better－best－first－search）算法

2.1 最好优先搜索存在的问题

图1中英文字母代表状态节点，括号中的数字代表每个状态节点的启发式值，大写字母G代表目标状态节点，实线代表搜索中的路径，括号中的数字代表状态节点的启发式值。如图1所示，如果采用最优优先搜索策略，最开始扩展状态节点B，然后，产生其后继状态节点，由于其后继状态节点的启发式值都比较小，所以会不断的扩展这些启发式值最小的状态节点，但这些后继状态节点并不是在目标路径上。如果，不单一地依赖最优状态节点，考虑更多的次优状态节点，那么在搜索过程中就有可能避免由于过度启发式函数指导搜索而导致的局部最优和高原状态。

如图1所示，通过增加状态节点选择的多样性，能够找 ｛A，C，J，O，T，G｝，｛A，D，K，P，G｝，｛A，E，G｝这几个质量较高的规划解。

2.2 算法基本思想

通过对最优优先搜索策略中存在问题的分析。我们可以从两方面来改善搜索策略：①将最优优先搜索中的开列表细化为多个包含不同启发式信息的列表，然后通过一定的概率来选择细化后的开列表，进而增加链表选择的多样；②每次选择多个状态节点进行扩展，而不仅仅只选择最优状态节点进行扩展。

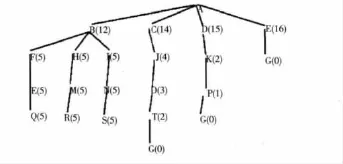
图1 局部最优和高原状态

相对于KBFS（K），本算法不仅仅选择单个列表中最优的K个状态节点，而是在多个列表中选择状态节点，BBFS能够有更大的可能来选择那些被错误估计为无利状态的节点。相对于自由走步，BBFS会将已经扩展的状态节点保存在关列表中，所以它可以有效地使用已经搜索到的状态空间。比如，当扩展的状态节点在多条不同的搜索路径上时，就可以直接利用以前的启发式值，而不再重复计算。BBFS是一个完备的算法。换句话说，就是在给定的时间和内存限制下，当存在规划解的时候，他可以返回一个规划解，当无法找到规划解时，它可以正确的退出。

2.3 算法实现步骤

算法1和算法2给出了BBFS的伪代码。算法1用于状态节点的扩展；算法2用于获取状态节点。BBFS整个算法的流程比较简单：从包含不同启发式信息的开列表中选择多个状态节点进行扩展后，再生成这些扩展状态节点的后继节点，直到找到规划解或者发现规划解不存在为止。BBFS旨在一定的范围内增加状态节点的多样性，而不是通过完全丢弃启发式信息来增加状态空间搜索的多样性，所以BBFS每次扩展的状态节点数即K值设置为5，这里的K值设定为5并不是必须的，在内存可以的情况下，K值可以适当设置大一点，比如K＝10。BBFS通过一个关列表保存所有已经扩展的状态节点，从而使得这些状态节点再次被扩展时，不再重新估计它们的启发式值，避免了自由走步的问题。当K个状态节点被扩展后，它们所产生的后继状态节点将放入包含不同启发式信息的开列表中。

算法1 Better－Best－First－Search

算法2get the K nodes from all of the open＿lists

算法1中，将初始状态节点放入任意的一个开列表中，然后进行扩展 （第1行）。全局变量gpselectsum用于表示所有开列表优先级的总和，gpselectopen＿list1用于表示包含FF启发式信息开列表的优先级，gpselectopen＿list2用于表示包含路标启发式信息开列表的优先级 （第4行～第6行）。开列表可以根据不同的规划器包含的启发式信息类型而设置，由于LAMA包含了FF和路标启发式信息，所以这里的开列表设置了两个：open＿list1，open＿list2。如果被扩展的状态节点是目标状态节点则返回规划解 （第12行～第14行）。每次扩展一个状态节点，如果该状态节点在open＿list1被发现且其启发式值比以前状态节点的启发式值小，则提高包含该状态节点列表的优先级，以期发现更多的有利状态节点，并修改gpselectsum的值 （第17行～第19行）。如果该状态节点在open＿list2被搜索到且其启发式值以前发现的启发式值小，则提高包含该有利状态节点列表的优先级，并修改gpselectsum的值 （第21行～第23行）。如果所有的开列表都搜索完成，还是没有搜索到规划解则返回失败信息。（第27行）。

算法2中，每从一个开列表中获取一个状态节点就降低该列表的优先级 （第7行）。主要是为了防止算法1中过度的增加单个列表的优先级，使得搜索多次在同一个列表中选择状态节点，不利于增加节点选择的多样性。同时，当在某个开列表出现了高原现象之后，通过减少该列表的优先级，选择另外的开列表，可以在一定程度避免这种高原状态。

参数Y （Y＞1）主要用于控制在不同开列表中状态节点被选中的可能性。BFS通常将所有产生的状态节点放在单个开列表中，然后再选择启发式值最小的状态节点进行扩展。BBFS通过将包含不同启发式信息的节点进行分类，归纳在多个开列表中。然后，每次扩展和获取状态节点时，就更新这些开列表的优先级，每个开列表以最高概率YP1／P2被选中，其中P1＝gpselectopen＿list1，P2＝gpselectopen＿list2。

如果BFS选中了一个无利状态节点，该无利状态节点的后继节点有一个较小的启发式值，它将会继续扩展该无利状态节点的后继，使得搜索的方向出现偏差。但是，当BBFS选中一个无利状态节点，即使该状态节点的后继的启发式值较小，它也不会立即扩展该状态节点的后继，而是选择另外的非该状态节点的后继状态节点，进行扩展。这样就在一定程度上避免了搜索陷入局部最优的问题。

3 实验结果分析

本文选取了问题规模较大的openstacks、nomystery规划域进行实验验证，其中每个规划域里面包含20个问题。这些规划问题全部来自2011国际规划大赛。实验环境是在单核处理器2.80Ghz AMD Athlon （tm）II X2 2400，内存2GB，Ubuntn－10.10 （Linux kernel 2.6.35－22－generic），编译器为g＋＋4.4.5的环境下进行地测试。设定规划超时限为规划大赛规定的30分钟 （1800s）。在LAMA中采用了两种启发式搜索算法，一种是最优优先，另一种的加权A＊，两种算法的搜索的基本流程差不多，差别在于启发式函数的代价计算方式不同。所以BBFS可以很好的与加权A＊结合。此次实验也将BBFS加入到加权A＊中。如图2所示，在状态空间较大的openstack领域，本文通过增加LAMA中状态节点选择的多样性，减少搜索对于启发式函数的依赖，缩短了规划解长度，DLAMA （Diversity－LAMA）表示在LAMA中采用了BBFS算法增加搜索中的多样性。这说明本方法在一定程度上避免了搜索中的局部最优和高原状态，改善了规划解的质量。

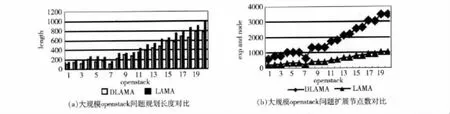
图2 DLAMA和LAMA规划长度和规划待代价对比，x轴代表规划问题的编号

表1和表2列出的是本文方法和LAMA对规划大赛中openstack和normstery领域实验的规划代价和规划步长。如表1所示，在大规模规划领域openstack中，虽然前3个规划问题DLAMA搜索到的规划代价比LAMA的高，但是其规划步长较比LAMA短，说明其在一定程度上避免了搜索中高原状态的出现，减少了规划步长。在后17个规划问题中，本方法搜索到的规划解在代价开销和规划步长方面都比LAMA好，主要原因在于：随着问题规模的逐步扩大，启发式函数对状态节点的估计变得越来越不准确，LAMA单一依赖启发函数进行搜索就会出现偏差，本方法通过增加状态节点选择的多样性，在一定程度上降低搜索对启发式函数的依赖，使得在搜索目标状态过程中能过纠正启发函数估计错误而导致的问题。由表2可知，在normstery领域中，LAMA的平均规划代价和规划步长为29.9，本方法的平均规划代价开销和规划长度为25.2。从上面的实验结果可以看出，本文提出的方法改善了规划解的质量。

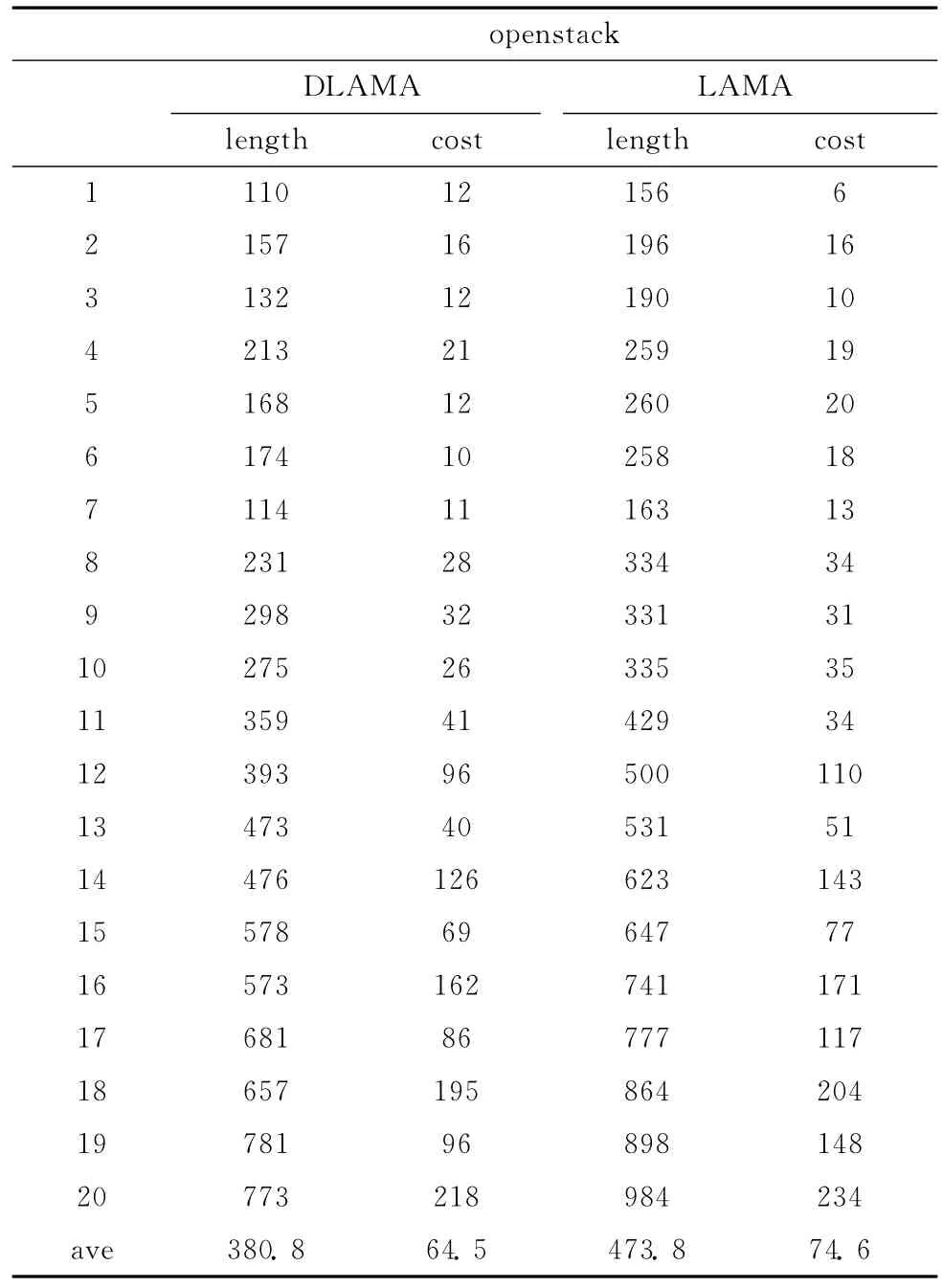
表1 openstack领域规划长度和规划代价比较

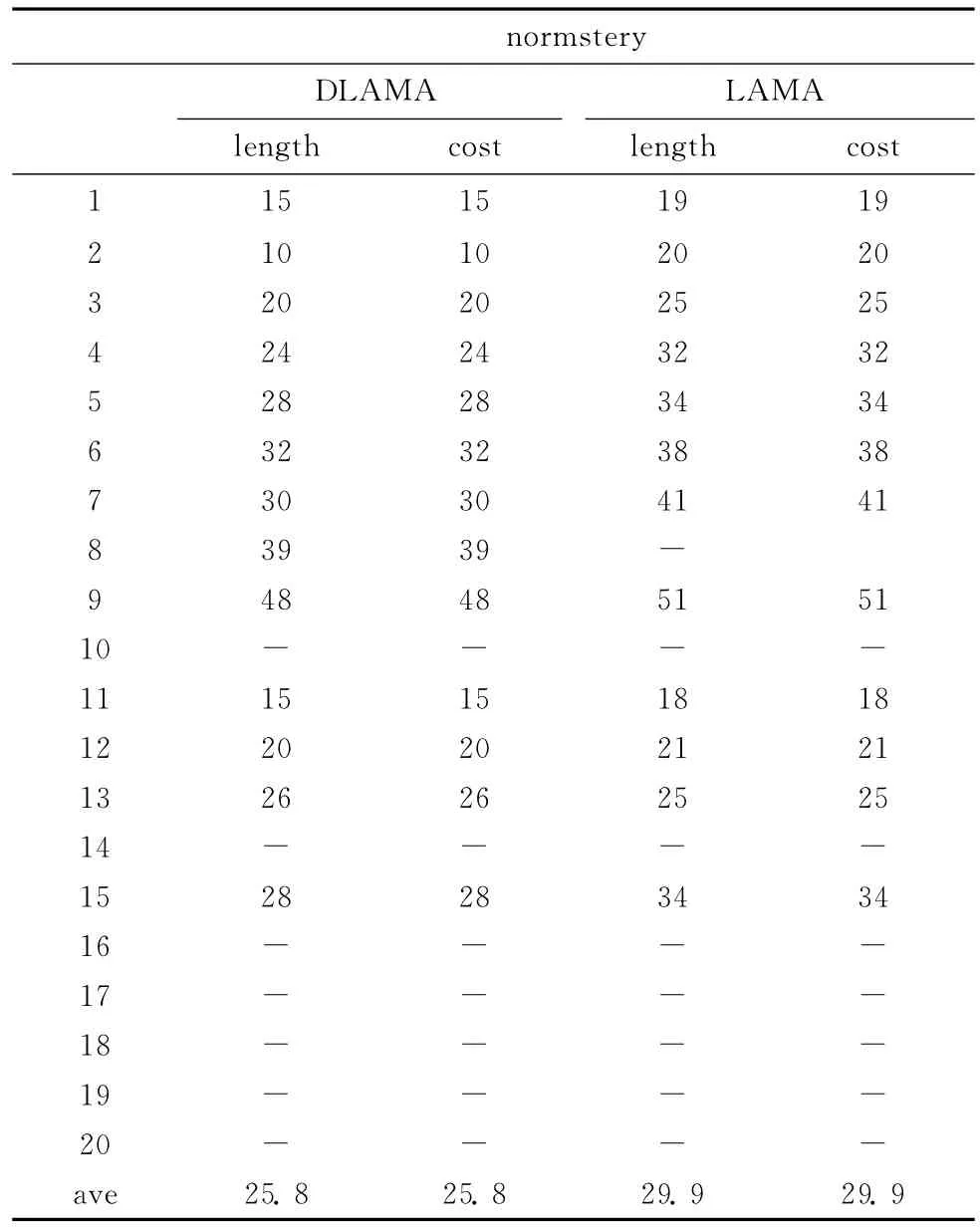
表2 normstery领域规划长度和规划代价比较

4 结束语

本文通过分析最优优先搜索策略单一依赖启发式函数指导搜索而导致的问题。提出了增加开列表多样性和状态节点选择多样性的方法，减少搜索对启发式函数的依赖，进而避免由于启发式函数估计错误而导致的局部最优和高原状态。该方法立足于在搜索过程中发现更多的路径，使得搜索不单一地选择估计的最优路径方向进行搜索，从而实现对规划质量的改善。实验结果表明，该方法是可行的。

然而，现实规划问题多种多样，本文所提出的方法只是在一定范围内增加了状态节点选择的多样性，随着更多复杂规划问题的出现，本方法在增加多样性方面也就有了进一步扩展的空间。可以在开列表选择方式中加入相关的启发式值参数，然后将参数Y的指数换成启发式值和各个开列表优先级的一个加权，通过这样来进一步增加搜索中选择的多样性，这是一个值得研究的方向。

［1］Helmert M.The fast downward planning system ［J］.Journal of Artificial Intelligence Research，2006，26 （1）：191－246.

［2］Richter S，Westphal M.The LAMA planner：Guiding costbased anytime planning with landmarks ［J］.Journal of Artificial Intelligence Research，2010，39 （1）：127－77.

［3］Lu Q，Xu Y，Huang R，et al.The roamer planner randomwalk assisted best－first search ［C］／／Proc International Plan－ning Competition，2011：73－76.

［4］Benton J，Talamadupula K，Eyerich P，et al.G－value plateaus：A challenge for planning［C］／／Proceedings of the International Conference on Automated Planning and Scheduling，2010：259－262.

［5］Eric A Hansen，Zhou Rong.Anytime heuristic search ［J］.Journal of Artificial Intelligence Research，2007，28 （1）：267－297.

［6］Richter S，Thayer J T，Ruml W.The joy of forgetting：Faster anytime search via restarting ［C］／／Proceedings of the Twentieth International Conference on Automated Planning and Scheduling，2010：137－144.

［7］Carlos Linares，Daniel Borrajo.Adding diversity to classical heuristic planning ［C］／／Proceedings of the Third Annual Symposium on Combinatorial Search，2010：73－80.

［8］Zhou R，Hansen E A.Breadth－first heuristic search ［J］.Artificial Intelligence，2006，170 （4－5）：385－408.

［9］Nakhost H，Müller M.Monte－Carlo explorationfor deterministic planning ［C］／／Proceedings of the Twenty－First International Joint Conference on Artificial Intelligence，2009：1766－1771.

［10］Maxim Likhachev，Anthony Stentz.R＊search ［C］／／Proceedings of the Twenty－Third AAAI Conference on Artificial Intelligence，2008：344－350.