K＋L次条件群签名：概念与构建

程小刚，杜吉祥

（1.华侨大学 计算机科学与技术学院，福建 泉州362021；2.南京航空航天大学 计算机科学与技术学院，江苏 南京210016）

0 引 言

K次条件群签名［1］是对传统群签名［2］的扩展，加上了次数限制，即只要签名的次数小于K，那么生成的签名是不可追踪的 （类似于环签名［3－4］），而当签名的次数大于K时，其生成的签名是可追踪的 （类似于群签名）。

本文考虑如下的进一步扩展的情形：K＋L次条件群签名，即小于K次签名是不可追踪的，K次之后的L次签名是可由群管理员 （GM）追踪的，再之后其生成的签名身份是公开的 （即任何人可追踪）。K＋L次条件群签名在签名次数小于K是可认为是类似环签名 （匿名且不可追踪），大于K小于K＋L时是群签名 （匿名但GM可追踪），大于K＋L是普通签名 （任何人可追踪）。

考虑如下应用场景：电子货币应用中，比如用签名作为货币，商家接收签名作为货币，只要签名验证通过就接收下来并提供商品或服务，然后商家向银行发送签名进行存款操作，此时银行根据此前所有接收的签名进行比较（相同的当然不能再接收）与追踪，只要此用户所做的签名次数不超过K次，那么追踪不到 （保证了用户的隐私性），要是超过K次，那么银行就能追踪到了并可以予以处罚，可见K在此可作为银行发给用户的电子货币的面值来使用；如果用户继续滥用其电子货币并超过了K＋L次，那么他的身份就公开可追踪了，即不仅银行，连公众也能找出他的真实身份了。

K次条件群签名构建的思想大致如下，GM （如银行）公布一个列表有K个随机值，用户在生成群签名时每次用其中的一个，只要用户的签名次数不超过K个，那么他的身份就是隐匿的，若超过K次，那么他就必须重复使用这K个随机值中的一个，那么他的身份信息就暴光了；对于K＋L次条件群签名的构建，也有一个K＋L随机值的列表，前面K个值是随机的且相互独立 （用户用它进行签名就是匿名的），而后面的L个随机值同前面的值是有秘密关系的 （比如离散对数），这个秘密信息由GM保存，这样只要用户做了超过K次，而小于K＋L次的群签名，GM就可以进行追踪 （外人没有此秘密信息，仍然不能追踪），而当用户做了大于K＋L次的群签名，他必须重用列表中的某个值，此时任何人都可以进行追踪了。

对于结合群签名与环签名特性已有了一些相关的工作，“可撤销环签名”［5］是在环签名的基础之上加入了追踪的功能 （并能自主选择能进行追踪的群体）；“条件环签名”［6］是在环签名中加入如下功能：签名者可通过一确认协议来证明某环签名是自己签的，而非签名者能否认不是自己发出的签名；“可追踪环签名”［7］中签名是不可追踪的，但如果对同一消息签了两次名 （如投了两次票），那么就可追踪其身份了；也有一些方案对环签名加入了追踪功能［8－9］；DAA（direct anonymous attestation）是群签名的一种变体［10］，群成员在签名是可自己控制匿名的程度 （即可控制两个群签名之间是否可链接）。

1 数学假设

本文用到了基于双线性群的一些数学假设，所以先给出双线性群的定义：

双线性群：设G和GT是阶为大素数q的群，并具有满足下列条件的映射e：G×G→GT：

（1）双线性性：对任意的a，b∈Zp，有e（aP，bP）＝e（P，P）ab；

（2）非退化性：对任意的生成元g，h∈G，有e（g，h）是GT的生成元；

（3）有效性：存在高效的算法能生成具有映射e的群G和GT，且有高效算法对任意的g，h∈G计算e（g，h）。

d－BDH （decisional Bilinear Diffie－Hellman）假 设：对任意的多项式时间敌手A，下列事件发生的概率是可忽略的 ｜Pr［A（aP，bP，cP，e（P，P）abc）＝ 1］－Pr［A（aP，bP，cP，T）＝1］｜，其中T是GT中的随机元素。

q－SDH （strong diffie－Hellman）假设：对任意的多项式时间敌手A，下列事件发生的概率是可忽略的：Pr［A（P，xP，x2P，…，xqP），其中c是任意随机数。

GT中的DDH （decisional diffie－Hellman）假设：对任意的多项式时间敌手A，下列事件发生的概率是可忽略的 ｜Pr［A（T，Ta，Tb，Tab）＝ 1］－ Pr［A（T，Ta，Tb，Tc）＝1］｜，其中T是是GT中的随机元素。

注意在此强调是GT中的DDH假设，因为由于双线性映射e的存在，在G中的DDH问题是容易解决的。

2 K＋L次条件群签名的定义与安全性需求

定义1 K＋L次条件群签名由下面6个算法构成：

（1）Setup：由 GM 生成公开参数，群公私钥 GPK和GSK；

（2）Join：用户可加入群中成为成员，获得GM颁发的成员证书，可用于生成签名；

（3）Sign：用户利用获得的成员证书可生成签名 （只要他签名的次数小于K，其身份是隐匿的，GM也不能追踪到）；

（4）Verify：任何人有群公钥都可验证某一签名是否合法 （即确信此签名由群中某人签发）；

（5）GM Trace：当其签名的次数大于K次且小于等于K＋L时，只有GM可用GM Trace算法对其进行追踪

（6）Public Trace：若某成员签名的次数超过了K＋L次，那么任何人可追踪出其真实的身份。

K＋L次条件群签名安全性需求如下：

正确性：要求一个诚实的用户加入群中成为群成员之后，可以生成签名并验证通过；

K－完全匿名性：诚实用户只要其签名的次数是小于等于K的，那么他的身份是完全隐匿的；

K＋1－GM可追踪性：某用户签名的次数超过K次以上，且小于等于K＋L次的，那么GM可追踪出他的身份；

K＋L＋1－公开可追踪性：某用户签名的次数超过K＋L次以上的，那么任何人可追踪他的身份；

不可伪造性：群外任何人不能生成合法验证通过的签名；

防陷害性：任何人 （包括GM）都不能冒充某成员生成合法的签名。

3 方案构建

基于［1］中的K－TAA方案，构建K＋L次条件群签名如下：

经由上述分析可以得知，实施高质量的改种果树造林作业设计十分具有必要性，不仅有助于为广大农民提供更多的就业机会，促使其可以经由劳务投入的方式获取收入，也有利于带动农村经济发展，推进社会主义新农村的建设进程，同时，在林地成林以后，相应区域土地的保肥保水能力也会大幅度提升，对后期各种作物更好的生长和发育具有积极意义，有助于获取到更多的经济效益。

Setup：GM选具有双线性映射的阶为素数p的群G和GT，e：G×G →GT满足e（aP，bP）＝e（P，P）ab，选P，P0，H←G，γ←Z＊P，群公钥GPK＝（P，Ppub，P0，H，Δ）；群私钥GSK＝γ；而且Ppub＝γP，Δ＝e（P，P）；并创建两个列表，List1有K＋L个随机元素对 （Θi，＾Θi）∈G×GT，前面K个都是相互独立的随机元素对，后面L个同前面的元素对有秘密关系 （即离散对数），GM掌握此秘密关系用于追踪 （见下 GM Trace），List2是 （i，β），i表示用户身份，β＝Δx，x是用户私钥；GM保存所有签名至一列表中 （如商家把用户的签名发给银行进行存款操作），且此列表是公众可访问的。

Join：此时用户和GM之间执行的一交互协议，完成后用户 获得成员 公 钥 mpk ＝ （a，S，C，β），而且用户 私 钥msk＝x，满足关系C＝xP，β＝Δx，协议如下：

（1）用户Ui选择随机的x’，r←，并把对x’的承诺C’＝x’P＋rH传给GM；

（3）Ui计算x＝y＋x’y’及 （C，β）＝（xP，Δx），再把 （i，β）加到List2中去，然后Ui将 （C，β）传给GM，并附上一标准的证明 PK｛（x，r′）：C ＝xP ∧yP ＋y′C′－C ＝r′H｝此PK表明C是正确地由C’，y，y’计算出来的，而且Ui知道x满足C＝xP；

（4）GM 验证 （i，β）存在于List2中，β＝e（C，P）且所附的证明是合法的。接着GM选取一随机的（此a要同以前GM颁发过的证书中的任一a都不同），计算S＝），并把 （S，a）传给 U；i

（5）Ui验证等式e（S，aP＋Ppub）＝e（C＋P0，P）是否成立，是的话则此Ui成为新成员，他的用户私钥msk＝x，他的公钥mpk＝ （a，S，C，β）。

Sign：第i次签名用 List1中的 （Θi，＾Θi），利用一CRH（collision resistant hash）函数H将第i个消息映射成Z＊p中的元素li，计算 （Γ，＾Γ）＝ （Θx，（Δl＾Θ）x），再生成PK｛（a，S，x）：（Γ，＾Γ）＝ （Θx，（ΔlΘ）x）∧e（S，aP＋Ppub）＝e（xP＋P0，P）｝，此表示一基于ROM模型的非交互零知识证明用户有秘密的 （a，S，x）满足后面的方程式，方程式中其他值都是已知的，构建方法如下：

（2）计算

注意在此把Hash函数H看成一随机语言器 （random oracle）；

（3）在ZP中计算s0＝k0＋cr3，s1＝k1＋cr1r2r4a，s2＝k2＋cr1r2r4，s3＝k3＋cr1r2r4x；

（4）输出签名为 （X，U1，U2，U3，c，s0，s1，s2，s3）；

Verify：检查等式e（U3，U1）＝？e（X，P）是否成立；再令T1’＝s1P＋s2Ppub＋s0H－cU2，T2’＝s3P＋s2P0－cX，Π1′＝ Θs3Γ－s2，Π2′＝＾Θs3＾Γ－s2，检查是否有：

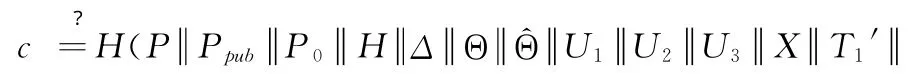
T2′ Π1′ Π2′）都成立的话接受签名，否则拒绝；

Public trace：为介绍简单起见我们先看Public Trace是怎么做的，用户做了K＋L次以上的签名，他必然重用了List1中的某个元素对 （因元素对只有K＋L个），则这两个签名的Γ 值是一样的，我们可以计算β，就可从List2中找到对应的用户i了；

4 安全性与效率

定理1基于d－BDH、q－SDH和GT中的DDH假设，及ROM模型，上述K＋L次条件群签名方案满足正确性、K－完全匿名性、K＋1－GM可追踪性、K＋L＋1－公开可追踪性、不可伪造性和防陷害性。

证明：（1）正确性：显然由方案的算法可见，诚实用户生成的签名能通过验证；

（2）K－完全匿名性：用户的签名由 （Γ，＾Γ，PK）构成，由PK的零知识特性可知PK部分不会泄露用户的任何身份信息，而Γ＝Θx，＾Γ＝＾Θx部分的确包含用户的身份秘密信息x，但基于d－BDH假设和群GT中的DDH假设，找出用户的真实身份计算上是不可行的：判断Γ＝Θx与List2中的β＝Δx是否为同一个x，是一个d－BDH难题；而判断＾Γ＝＾Θx与β＝Δx是否为同一个x，是一个GT群中的DDH难题；

在此我们指出由于双线性映射e，在群G中DDH问题是可解的，因而同一用户做的签名虽然是匿名的，但是可链接的，为克服这一问题，可采用 “非对称”的双线性映射e：G1×G2→GT，其中G1和G2是不同的群，而且DDH假设在G1、G2中都成立；

（3）K＋1－GM可追踪性：用户做了K次以上的签名后，必然用了List1中后面L个随机元素对中的一个，而这些元素对同前面的元素对是有秘密关系的如ΘK＋1＝Θr1，＾ΘK＋1＝ ＾Θr1， 且 GM 知 道 此 秘 密 的 r， 那 么 ＾ΓK＋1＝（ΔlK＋1＾ΘK＋1）x，＾Γ1＝ （Δl1＾Θ1）x，则：

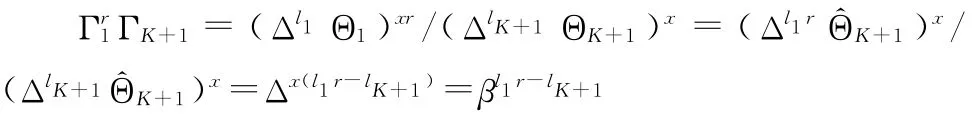
GM通过尝试List2中的每一个β是否满足上式即可找出签名者；

（4）K＋L＋1－公开可追踪性：用户做了K＋L次以上的签名，必然重用了List1中元素对中的某一个，则这两个签名的Γ值是一样的，而＾Γ值是不一样的 （因用的l值不一样），则可计算Δx＝β，解出β，从而可在List2中找出实际签名者；

（5）不可伪造性：方案中的用户证书中的S实际上是GM对a的BB签名，那么由BB签名［11］的安全特性，在q－SDH假设之下，GM之外的任何人都不能生成这样的 （S，a）签名／消息对，即任何群外的人都不能生成合法的签名；

（6）防陷害性：在用户加入群时，与GM执行交互协议后，GM得到C，用户的到私钥x满足C＝xP，注意GM是不知道此x的 （由离散对数假设，GM也计算不出此秘密），那么GM就不能冒充此用户进行签名操作，其他人当然也不能冒充此用户进行签名操作。

由上述构建可见，签名与验证的计算量都是常数级的O（1），比较高效；Public Trace的计算量也不大，假设所有的签名已排好序，则通过二分查找，可在O（logM）时间里找到重复的Γ值 （M为到当前为止所有的签名数量）；找到后可计算出β，在List2中找出对应的用户i也只需要O（logN）工作量 （N为用户数量），所以Public Trace的效率为O（logM＋logN）；但GM Trace的工作量较大，分析如下：GM收到一用List1中K＋1项的签名后，要找出此用户，必须对前面的每一个签名中Γi的计算其r次方，判断是否与当前的Γ值相同，显然工作量为O （M）；找到后可计算出＾Γri／＾Γ ，再对List2中的每一个β计算βlir－l，看其是否与＾Γri／＾Γ相等来找出到底是哪个用户作的签名，此举显然工作量为O（N），所以GM Trace的工作量为O（M＋N），效率相对较低。

5 结束语

本文提出了一种新的K＋L次条件群签名的概念，扩展了原有的K次匿名认证的概念，可适用于范围更广的应用场合；给出了其定义与安全性需求，并基于d－BDH、q－SDH假设给出了一个具体方案的构建；不足之处在于方案的安全性基于ROM模型、GM追踪的效率不高，下一步工作是研究如何提高效率，及在标准模型下构建安全的K＋L次条件群签名。另外，考虑对其他或更一般的条件 （如限制可签署的支票金额等），如何构建条件群签名方案，也是值得研究的课题。

［1］Teranishi I，Furukawa J，Sako K.K－times anonymous authentication［J］.IEICE Transactions on Fundamentals of Electronics，Communications and Computer Sciences，2009，92－A（1）：147－165.

［2］MA Haiying，WANG Zhanjun.Full anonymous dynamic short group signature scheme［J］.Computer Engineering and Design，2010 （6）：1222－1225（in Chinese）. ［马海英，王占君.完全匿名的动态短群签名方案 ［J］.计算机工程与设计，2010（6）：1222－1225.］

［3］WANG Huaqun，JIANG Guoxing，ZHAO Shuping.Efficient ring signature scheme from bilinear pairings［J］.Computer Engineering and Design，2008，29 （6）：1459－1461 （in Chinese）.［王化群，姜国兴，赵树平.高效的基于双线性对的环签名方案 ［J］.计算机工程与设计，2008，29 （6）：1459－1461.］

［4］GE Aijun，MA Chuangui，ZHANG Zhenfeng，et al.Identitybased ring signature scheme with constant size signatures in the standard model［J］.Chinese Journal of Computers，2012，35（9）：1874－1880 （in Chinese）.［葛爱军，马传贵，张振峰，等.标准模型下固定长度的基于身份环签名方案 ［J］.计算机学报，2012，35 （9）：1874－1880.］

［5］LIU D Y W，LIU J K，MU Y，et al.Revocable ring signature［J］.Journal of Computer Science and Technology，2007，22（6）：785－794.

［6］ZENG S.An efficient conditionally anonymous ring signature in the random oracle model ［J］.Theoretical Computer Science，2012，461 （23）：106－114.

［7］Fujisaki E，Suzuki K.Traceable ring signature ［G］.LNCS 4450：Proceedings of Public Key Cryptography－PKC，Heidelberg：Springer，2007：181－200.

［8］SUN Qingying，WU Keli，XU Huiyan.Signer－traceable ring signcryption scheme ［J］.Computer Enginee－ring，2011，37（16）：129－131（in Chinese）. ［孙庆英，吴克力，徐会艳.一种可追踪签名者的环签密方案 ［J］.计算机工程，2011，37（16）：129－131.］

［9］HUANG Dawei，YANG Xiaoyuan，CHEN Haibin.Ring signature scheme with revocable anonymity［J］.Computer Engineering and Applications，2010，46 （24）：88－89 （in Chinese）.［黄大威，杨晓元，陈海滨.一种可撤销匿名性的环签名方案［J］.计算机工程与应用，2010，46 （24）：88－89.］

［10］SONG Yang，LI Lixin，ZHOU Yanzhou，et al.Security analysis and improvement of DAA protocol［J］.Computer Engineering and Design，2010 （1）：26－29 （in Chinese）. ［宋扬，李立新，周雁舟，等.DAA协议的安全性分析及改进 ［J］.计算机工程与设计，2010 （1）：26－29.］

［11］JAO D，Yoshida K.Boneh－boyen signatures and the strong diffie－hellman problem ［G］.LNCS 5671：Pairing－Based Cryptography－Pairing，2009：1－16.