基于多准则决策的软件可靠性模型选择方法

韩 坤，吴 纬，何成铭，曹军海

（1.装甲兵工程学院 技术保障工程系，北京100072；2.北京特种车辆研究所，北京100072）

0 引 言

软件可靠性模型在软件可靠性评估和预计方面发挥着关键作用，但是，数量众多的软件可靠性模型给模型的应用带来了极大的困难，如何选择合适的软件可靠性模型成为急需解决的问题［1］。目前所提出的软件可靠性模型选择方法可分为两类：基于模型评价准则的方法和基于模型聚类的方法。基于模型评价准则的软件可靠性模型选择方法首先将失效数据应用于软件可靠性模型，然后用模型评价准则对模型输出结果进行评价，评价结果作为进行模型选择的依据［2］。常用软件可靠性模型评价准则有模型拟合度、预计有效性、模型偏差、模型偏差趋势和噪声等。基于模型聚类方法的思路是，具有相似特征的软件失效数据适用于相同的软件可靠性模型［3］。建立一个软件可靠性模型选择平台，包括多组基准软件失效数据，以及每组数据所适用的软件可靠性模型。通过将目标数据与基准数据进行比照，如果两组数据特征相同，则基准数据对应的模型同样适用于目标数据，平台中的基准数据和模型可以动态更新。以上两种方法都被证明是可行的。但它们都各有缺陷，基于模型评价准则的方法要求将全部候选模型应用于失效数据，并对模型结果进行评价，运算量大，且没有提供选择候选模型的方法；基于模型聚类方法的使用要求积累大量具有典型特征的失效数据以及所适用的模型。这些约束条件都在一定程度上限制了这些方法的使用。针对这些问题，本文提出直接指导软件可靠性模型选择的若干准则，并阐述基于这些准则进行软件可靠性模型选择的算法，以简化软件可靠性模型选择工作。

1 软件可靠性模型分类

从1972年Jelinski－Moranda模型被提出至今，已经有一百余种软件可靠性模型公开发表［4］。这些模型可以归为两类：可靠性早期预计模型和基于运行的可靠性模型。早期阶段是指软件在可运行之前的阶段，包括方案论证、系统定义、需求分析、设计、编码和单元测试阶段。软件可靠性早期预计模型根据软件生命周期的早期阶段，特别是测试之前的需求分析和设计阶段的评审结果，对后续阶段的软件潜在缺陷进行预计，为更早地采取预防和纠正措施，改进软件开发过程和提高软件产品可靠性提供必要的信息。由于没有软件运行失效数据，早期阶段的可靠性预计通常是根据软件可靠性影响因素分析，影响因素有软件的应用类型 （机载、过程控制、开发等），固有特征 （应用、任务、功能、接口等），开发特征 （避错、容错措施），开发方的能力成熟度等级，软件规模和复杂度等。这类模型有美国空军Rome实验室开发的早期预计模型、Samuel Keene的开发过程模型 （DPPM）和Rayleigh早期预计模型等［5］。

从系统测试开始，软件进入可运行阶段，包括系统测试、确认测试和使用阶段。基于运行的软件可靠性模型根据软件系统运行失效数据，对软件系统的失效率进行评价和预计。这类模型以概率论和数理统计为基础，将软件可靠性测试和使用中发生失效的过程看作随机过程，使用各种分布函数来描述软件失效过程。并将软件失效数据视为随机分布数据，基于软件失效数据对分布函数的参数进行估计，得到模型的具体表达式，从而评价和预计软件的可靠性。基于运行的软件可靠性模型一般对故障发现和排除过程做出诸多假设，如软件测试用例代表软件实际使用剖面，软件失效率与潜在故障数成正比等，这些假设决定模型的形式和模型参数的意义［6］。基于运行的软件可靠性模型是最早应用于软件可靠性工程领域的传统分析模型，具有坚实的理论基础和丰富的实践经验，现有的软件可靠性模型也大多属于这类模型。目前市场上发行的软件可靠性计算机辅助分析软件，如计算机辅助软件可靠性评估（CASRE）和软件可靠性统计建模和评估 （SMERFS）等，都是应用该类模型进行软件可靠性分析的［7］。通过对现有软件可靠性模型进行梳理分类，能够帮助我们更快找到所需的模型。

2 软件可靠性模型选择准则

基于使用需求和软件可靠性模型的特点，提出五项软件可靠性模型选择准则，包括生命周期阶段、模型输入要求、模型输出要求、模型假设吻合和失效数据趋势准则，其中，前三项为确定性准则，所选的模型需要完全符合这些准，后两项为不确定性准则，所选模型不一定能够完全符合，优先选用符合程度较高的模型。

2.1 生命周期阶段

软件可靠性模型被应用在软件生命周期的不同阶段，因此，有必要确定哪些模型适用于某个特定阶段。适用于各个生命周期阶段的典型软件可靠性模型如图1所示［8］。

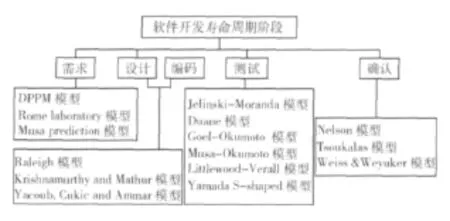
图1 适用生命周期各阶段的典型软件可靠性模型

（1）在软件论证和需求分析阶段，只有软件应用类型和开发方能力成熟度等级等少量信息，可选用Rome实验室早期预计模型、DPPM模型等［9］；

（2）在设计和编码阶段，根据阶段审查和评审得出的错误报告信息对可靠性进行预计，可选用Raleigh模型等；

（3）在测试阶段，软件中的错误不断被发现和排除，可选用软件可靠性增长模型；

（4）在确认阶段，对发现的错误不做更改，因此可以认为软件的失效率是固定的，可选用Nelson模型等。

2.2 模型输入要求

不同的软件可靠性模型对输入数据的要求可能不同，根据收集到的数据类型，选用适合的模型。

（1）软件可靠性早期预计模型的输入要求为软件可靠性影响因素，如软件规模、复杂度、重用代码比例、编程语言、开发方的能力成熟度等级等；

（2）基于失效时间序列的软件可靠性模型输入要求为软件每次失效的时刻；

（3）基于失效时间间隔的软件可靠性模型输入要求为相邻失效的时间间隔；

（4）基于失效计数的软件可靠性模型输入要求为单位时间内的失效次数。

另外，有些软件可靠性模型要求输入基于日历时间的失效数据，其它一些模型则要求输入基于CPU时间的失效数据等［10］。

2.3 模型输出要求

不同的软件可靠性模型用户可能期望不同的输出。

（1）在进行软件可靠性测试之前，希望得到软件潜在故障数，以便合理安排测试时间和测试所需资源；

（2）在软件可靠性增长测试期间，希望得到达到某预期可靠性目标所需的时间；

（3）在软件可靠性验证测试期间，希望得到软件失效率或平均故障间隔时间 （MTBF）；

（4）对规定的时间内，不允许发生工作失效的重要系统，即对可能因故障中止工作而造成人员伤亡或重大经济损失的软件产品，要求失效率 （）数据；

（5）对软件发生故障时，只影响系统部分非关键功能但系统不失效、且允许并预定要维修的软件，输出一般要求MTBF或可导出MTBF的数据。如果对模型输出的要求为 MTBF，则不可选用 Goel Okumoto NHPP模型［11］。

2.4 模型假设吻合

软件可靠性模型都是基于各种假设。然而，并不是所有假设都可以完全吻合。假设条件吻合程度高的模型应优先选择。基于假设条件的不同，软件可靠性模型可以划分为以下四类［12］：

（1）马尔科夫模型。基本假设是软件失效服从马尔科夫过程。这类模型的主要特征是，在某一特定时刻，软件具有有限的多种状态，各状态之间的转移概率只与当前状态有关。软件的失效率是基于当前软件状态的离散函数。这类模型有Jelinski－Moranda模型和Schick－Wolverton模型等。

（2）非齐次泊松过程模型。基本假设是软件失效过程为非齐次泊松过程。这类模型的主要特征是，均值函数被定义为在某给定时刻之前的期望失效数，根据情况选择适用的均值函数。这类模型有Goel－Okumoto模型和Schneidewind模型等。

（3）输入域模型。基本假设是软件测试用例能够代表软件实际使用剖面。基于软件的实际使用剖面，随机选择输入数据，研究导致软件失效的概率。根据一系列测试用例的输入结果，计算软件的可靠性。这类模型有Brown－Lipow模型和Nelson模型。

（4）基于软件工程度量的模型。基本假设是规模越大、复杂度越高的软件会具有更多的缺陷数，且不同的软件类型和开发特征会影响软件产品的可靠性。软件工程度量被用于预计软件的缺陷数。这类模型有基于Halstead度量的模型和基于McCabe度量的模型。

2.5 失效数据趋势

将失效数据呈现的趋势与软件可靠性模型描述的趋势相比较，如果两者相似，则此模型的预计精度会相对较高。失效数据趋势可以分为以下四类。

（1）失效数据趋势为可靠性增长。软件可靠性增长测试和系统使用期间，随着软件错误的不断排除，并且在不引进新错误的情况下，软件可靠性呈逐渐增长趋势。这种情况下，一般选用软件可靠性增长模型，如Goel－Okumoto模型和Musa－Okumoto模型。

（2）失效数据趋势为可靠性先下降后增长。在测试初期，软件存在的错误较多，但由于测试人员对软件本身及测试环境不熟悉，导致发现的错误较多，得以改正的错误较少。因此，软件可靠性呈下降趋势。随着测试人员熟练程度的提高，软件错误不断得到更正，可靠性也随之增长［13］。推荐选择S型模型，如Yamada S型模型。

（3）失效数据趋势为可靠性稳定。这种情况一般发生在软件生命周期的后期，随着软件故障的不断排除，软件缺陷不再频繁引起系统失效，软件失效发生的次数减少，软件错误排除周期变长，软件可靠性呈现稳定，可以选择线性模型或泊松模型［14］。

（4）失效数据趋势为可靠性不断下降。这种情况一般是由于软件错误排除过程中，同时引入了新的错误。此时，已经失去了应用软件可靠性模型的意义。应该及时审查和调整软件错误的排除过程，保证不引入新的软件错误。

3 软件可靠性模型选择算法

根据上述软件可靠性模型选择准则，基于多准则决策进行软件可靠性模型选择的基本思路如图2所示。

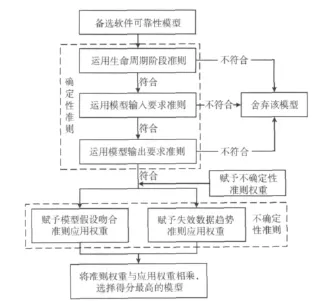
图2 基于多准决策的软件可靠性模型选择算法

首先，运用确定性准则对软件可靠性模型进行筛选。经过运用生命周期阶段、模型输入要求、模型输出要求三项确定性选择准则，只有适用于特定生命周期阶段，满足模型输入和输出要求的模型被保留下来做为候选模型。

其次，对不确定性准则赋予准则权重。根据用户需求和模型应用特点，按准则的重要程度对模型假设吻合准则和失效数据趋势准则分别赋予准则权重，要求两准则权重相加等于1。

再次，对候选模型赋予准则应用权重。将模型假设吻合准则和失效数据趋势准则分别应用于各候选模型，根据软件可靠性模型对准则的满足程度，赋予0和1之间的值作为应用权重。

最后，将各候选模型的准则权重和相应的应用权重相乘，选择得分最高的软件可靠性模型。

4 实例应用

选用一组某型软件系统测试期间的失效数据，如表1所示，运用所提出的方法进行软件可靠性模型选择，用于评估软件当前的可靠性水平。

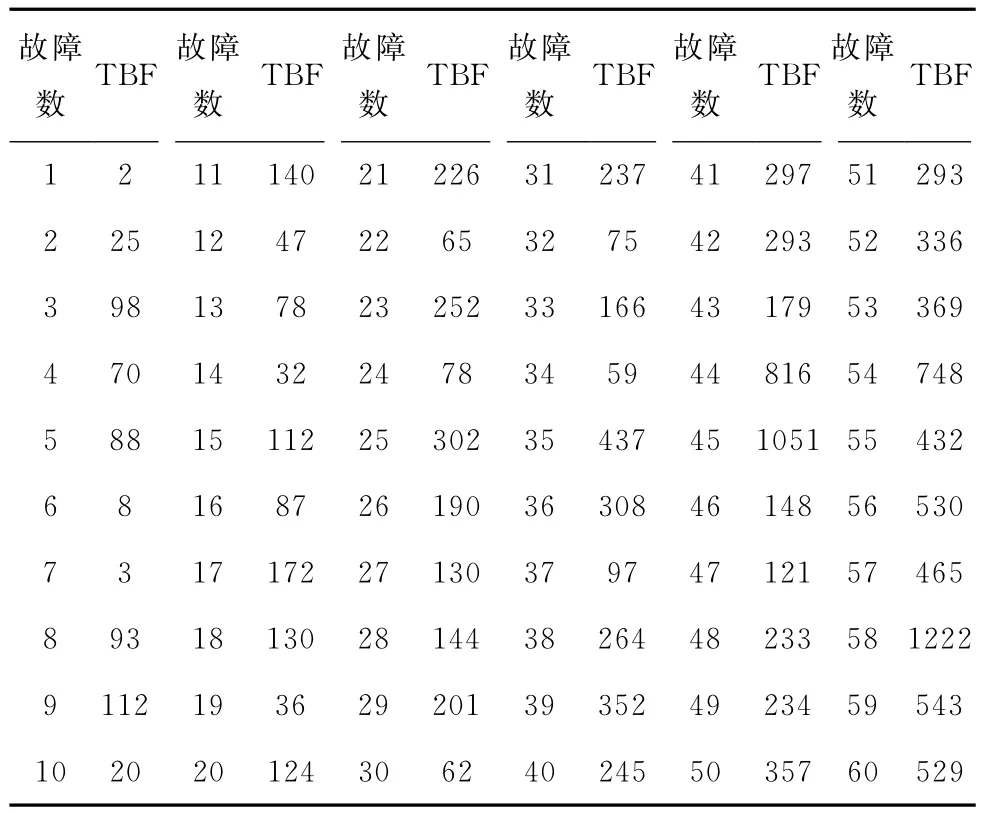
表1 软件系统测试失效数据

（1）此失效数据产生于系统测试阶段，根据软件生命周期阶段准则，选择适用于系统测试阶段的软件可靠性模型。系统测试阶段常用的模型有：Jelinski－Moranda（JM）模型、Duane模型、Goel－Okumoto （GO）模 型、Musa－Okumoto（MO）模 型、Littlewood－Verall （LV）模 型、Yamada S－shaped （YS）模型等；

（2）此失效数据是软件失效时间间隔数据，但能够转化为软件失效时刻数据和软件失效计数数据。由于第一步所选模型都属于基于运行的软件可靠模型，满足模型输入要求准则；且皆可以输出失效率数据，适用于评估软件系统当前的可靠性，满足模型输出要求准则。所以，保留所有第一步选择的模型做为候选模型；

（3）候选模型皆是对软件失效过程做出假设，这种情况下失效数据趋势准则更为重要，因此，分别赋予模型假设吻合准则和失效数据趋势准则的准则权重为0.3和0.7。

（4）根据软件失效过程与模型假设的吻合程度，各候选模型基于模型假设吻合准则的应用权重分别为：JM＝0.25，Duane ＝ 0.5，GO ＝ 0.5，MO ＝ 0.5，LV ＝0.25，YS＝0.5。

根据失效数据趋势和模型曲线趋势的相似程度，各候选模型基于失效数据趋势准则的应用权重分别为：JM＝0.2，Duane＝0.4，GO ＝0.4，MO ＝0.5，LV ＝0.3，YS＝0.1。

各候选模型的最终得分分别为：JM ＝0.25＊0.3＋0.2＊0.7＝0.215，Duane＝0.5＊0.3＋0.4＊0.7＝0.43，GO ＝0.5＊0.3＋0.4＊0.7＝0.43，MO＝0.5＊0.3＋0.5＊0.7＝0.5，LV ＝0.25＊0.3＋0.3＊0.7＝0.285，YS＝0.5＊0.3＋0.1＊0.7＝0.22。

Musa－Okumoto（MO）模型得分最高，所以最终选择Musa－Okumoto （MO）模型。

5 结束语

本文分析了现有软件可靠性模型选择方法，指出它们存在运算量大、应用不方便等缺点。提出可以直接指导软件可靠性模型选择的若干准则，阐述了基于这些准则进行软件可靠性模型选择的算法，并进行了实例应用。相对现有基于模型评价准则和模型聚类的软件可靠性模型选择方法，本文所提出的方法计算简单，对经验数据的积累要求较低，可以大大减少进行软件可靠性模型选择的工作量。但也应该看到基于模型选择准则方法的不足，基于此方法选择出来的软件可靠性模型，还需要用模型评价准则对其应用效果做出最终评价。进一步研究的方向是将三种方法综合起来，在没有历史数据的情况下，首先基于软件可靠性模型选择准则，选出适量得分排名靠前的模型作为侯选模型；其次，将各侯选模型应用于软件失效数据，并基于软件可靠性模型评价准则对各侯选模型的应用效果进行评价，选择评价结果最好的模型作为最终模型；最后，通过对软件失效数据和适用模型的积累，建立利于工程化应用的软件可靠性选择平台。

：

［1］Karanta Ilkka.Methods and problems of software reliability estimation ［R］.Finland：VTT Technical Research Centre of Finland，2006：48－49.

［2］TENG Lingling，SHAO Dong，RONG Guoping.Reseach on software reliability model selection ［J］.Computer Applications and Software，2010，27 （6）：128－131 （in Chinese）.［腾灵灵，邵栋，荣国平.软件可靠性模型选择研究 ［J］.计算机应用与软件，2010，27 （6）：128－131.］

［3］Kapil S，Rakesh G，Nagpal C K.Selection of optimal software reliability growth models using a distance based approach ［J］.IEEE Transactions on Reliability，2010，59 （2）：266－276.

［4］ZHU Lei，YANG Dan，WU Yingbo.Selection of software reliability model based on BP neural network ［J］.Computer Engineering and Design，2007，28 （17）：4091－4094 （in Chinese）.［朱磊，杨丹，吴映波.基于BP神经网络的软件可靠性模型选择 ［J］.计算机工程与设计，2007，28 （17）：4091－4094.］

［5］IEEE Std 1633TM－2008，IEEE recommended practice on software reliability ［S］.

［6］SHI Zhu.Software reliability engineering ［M］.Beijing：Beijing University of Aeronautics and Astronautics Press，2009 （in Chinese）.［石柱，软件可靠性工程 ［M］.北京：北京航空航天大学出版社，2009.］

［7］Lyu M R.Software reliability engineering：A roadmap ［C］／／Proceedings of Future of Software engineering，2007：153－170.

［8］Pham H.System software reliability ［M］.London：Springer Publisher，2006：132－134.

［9］Wende Kong.Towards a formal and scalable approach for quantifying software reliability at early development stages ［D］.Maryland：University of Maryland，2009：12－15.

［10］Norman Schneidewind.Comparison of reliability and testing models ［J］.IEEE Transactions on reliability，2008，57 （4）：607－615.

［11］WEI Ying，SHEN Xiangheng.Analysis and establishment of software reliability parameters of astronautics payload software［J］.Computer Engineering and Design，2008，29 （10）：2564－2566（in Chinese）.［魏颖，沈湘衡.航天载荷应用软件可靠性参数的分析与确立 ［J］.计算机工程与设计，2008，29（10）：2564－2566.］

［12］CHAO Bing.The classiftcation of software reliability models and failure analysis of software reliability based on support vector machines ［D］.Wuhan：Wuhan University，2010：11－19（in Chinese）.［晁冰.基于支持向量机的软件可靠性模型分类及失效分析 ［D］.武汉：武汉大学，2010：11－19.］

［13］WU Y P，HU Q P，XIE M.Modeling and analysis of software fault detection and correction process by considering time dependency ［J］.IEEE Transactions on Software Reliability，2007，56 （4）：629－642.

［14］LU Minyan.Software reliability engineering ［M］.Beijing：National Defense Industry Press，2011 （in Chinese）.［陆 民燕.软件可靠性工程 ［M］.北京：国防工业出版社，2011.］