立式三轴搅拌釜固－液悬浮特性的数值模拟

赵丽君 尹 侠

（南京工业大学机械与动力工程学院，江苏 南京 211816）

搅拌设备是现代工业生产中典型的过程设备之一，在石油化工、医药、食品、造纸、冶金、环保等行业都有着广泛的应用。随着计算流体力学（CFD）技术的发展，对给定条件下搅拌槽内流体的流动状态进行预测已经成为可能，越来越多的学者采用此方法对搅拌槽内流场进行模拟［1，2］。

固液搅拌是工业搅拌设备中比较常见的一种操作，且固液悬浮作为两相流问题要比单相流复杂得多，近几年对其研究渐渐增多。对于立式单轴搅拌槽内固液混合过程的研究已较成熟［3－5］，但对立式多轴搅拌槽内固液混合过程的模拟还未见报道。相比于传统的立式单轴搅拌槽，立式三轴减小了桨叶加工的难度，降低了对搅拌轴强度以及减速器的要求，并且降低了设备的制造成本［6］。本试验利用FLUENT软件对立式三轴搅拌釜内的两相混合进行了数值模拟，得到搅拌槽中液体的流动状况和固相分布情况。对固液两相流的流场分布规律进行研究，得到最佳搅拌速度和完全离底悬浮所需最低搅拌功率。为此种结构的工业设计提供一定的参考。

1 数学物理模型和计算模拟方法

1.1 搅拌器模型

为验证数值模拟方法的可靠性，建立计算物理模型如下：搅拌槽为圆柱型平底容器，直径（D）2m，高（H）0.8m。搅拌桨桨型CBYIII（桨径d＝0.174m），三桨均布。液位高度HL＝0.6m，两物相系采用玻璃珠－水体系，固体体积分数为0.11，直径为50～150μm，其几何模型见图1。计算时采用非结构化网格（见图2），其网格数为586 318。

1.2 多相流模型

采用欧拉－欧拉模型描述固液两相流，欧拉－欧拉法是把颗粒作为拟流体，认为颗粒与流体是共同存在相互渗透的连续介质，颗粒与流体之间的藕合是通过动量交换项以及连续相作用在分散相上的曳力得到的。且固液两相间动量交换使用Wen－Yu模型，其连续性方程和动量方程如下［7］：

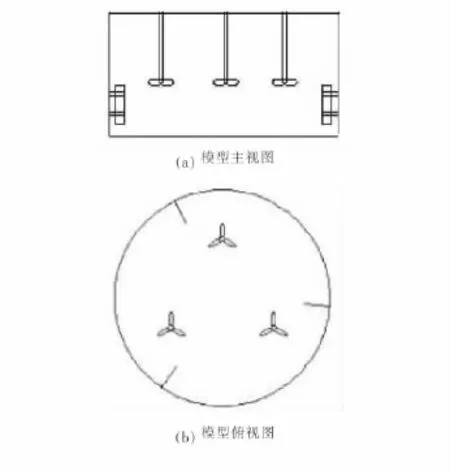
图1 立式三轴搅拌釜几何模型Figure 1 Geometric model of vertical three－impeller stirred tank

图2 搅拌釜内的网格划分Figure 2 Grids for the stirred tank

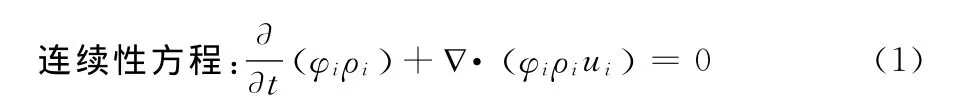
连续相和离散相动量方程分别为：

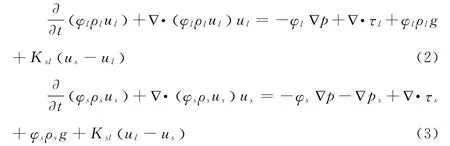
其中两相间动量交换因数Ksl：

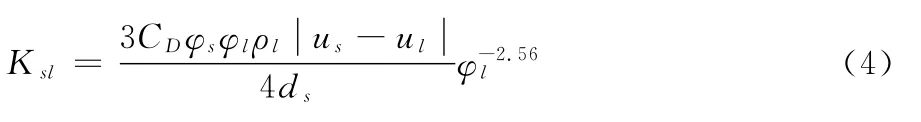
曳力系数CD：

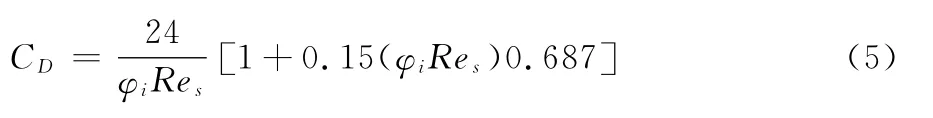
式中：

φi—— 物相体积分数，%；φl——液相体积分数，%；

φs——固相体积分数，%；

ρi—— 物相密度，kg／m3；

ρl—— 液相密度，kg／m3；

ρs—— 固相密度，kg／m3；

ui—— 物相速度矢量，m／s；

ul—— 液相速度矢量，m／s；

us—— 固相速度矢量，m／s；

τl—— 液相压力应变张量；

τs——固相压力应变张量；

g—— 重力加速度，m／s2；

ds——固体颗粒直径，m；

Res—— 雷诺数；

P——功率，W。

1.3 计算模拟及边界条件

采用FLUENT6.3软件对搅拌器内的两相混合进行数值模拟，选用三维稳态求解器，液相湍流模型采用标准k－ε模型，计算采用多重参考系法（MFR），配合欧拉－欧拉多相流模型。压力速度耦合采用SIMPLEC算法，差分格式使用一阶迎风，残差设为1e－6。计算时监视变量（速度、槽底平均固含率）趋于稳定值时认定为计算收敛。

2 数值模拟结果分析

2.1 CFD模拟的流场固相浓度分布

在搅拌过程中，固相粒子受两个力的作用：① 流体流动的剪切力；② 固体颗粒本身的重力。最终固体粒子沉积的位置为这两个力综合作用的结果。改变桨叶搅拌速度分别为330，440，550r／min，折合叶端线速度分别为3，4，5m／s。分别对其进行模拟，达到计算收敛时观察槽底固体浓度分布见图3。由图3可知，随转速的增大，沉积面积越来越小，槽底固相平均浓度逐渐降低，槽中心浓度也逐渐降低。3个桨叶的正下方均有一片低固含率区，对应着图5中的由叶轮排出流撞击槽底形成的高速区；而两个搅拌器之间存在颗粒沉积区，此区的流场速度主要由叶轮底部流体与其传质形成，速度相对较小，易造成颗粒沉积，但随着转速增大，沉积面积逐渐减小至消失；对于槽底两桨叶间靠近槽壁的区域，由于本试验采用平底模型，此区域易产生搅拌死区，但随着转速的增大，此区域面积也越来越小。所以为了减小搅拌死区，可以适当增大桨叶叶端转速。由此规律和现象可以看出：CFD模拟结果中槽底沉积带的大体形状和位置与试验结果有较好的一致性。

2.2 固体粒子对流场的影响

图4为搅拌槽在转速N＝550r／min搅拌时，双桨叶面单相流场与多相流场速度图。由图4可知，由于固体粒子的加入，桨叶排出流的锥形角变大，槽中心处的轴向流变得并不明显；整体循环在单相中约为0.8 HL，但在多相中仅达到0.4 HL高度时变折回桨叶区，对应固体悬浮高度约为0.4 HL，这将导致槽体上端固相浓度较低。所以当搅拌轴结构与安装位置选取不当时中心部分速度较小，易造成中心部分出现固相堆积。

图3 不同叶端线速度下模拟（左）与试验（右）槽底固相浓度分布图Figure 3 Solid phase concentration distribution under different agitating blade tip speed at the groove bottom for simulation（left）and experiment（right）

图4 速度为550r／min时单相流和多相流场的速度矢量图Figure 4 Speed vector－graph for single－phase flow and multiphase flow field at speed 550r／min

为了更清楚的描述搅拌流场中的速度矢量，对单相流场和多相流场搅拌槽槽底z＝0m和液面z＝0.6m横截面分别进行截取，其速度矢量图见图5。从z＝0m截面图中可以看出：槽底在搅拌器正下方的速度矢量是向斜上方四周发散的，这使得槽底流体向上方及四周运动，对于槽底颗粒达到完全离底悬浮是很有帮助的；且多相较单相，槽中心及两桨叶间靠近槽壁的区域速度值明显降低。所以在这些区域中固体粒子容易堆积。从z＝0.6m即液面速度矢量图可以看出：多相速度受各自搅拌桨影响比单相小，开始绕着搅拌槽中心整体旋转，轴向运动变得很微小。所以将导致搅拌过程中，其与槽下方传质较少，浓度较低。当搅拌速度不够时，不易于槽内整体固相的均匀悬浮。

图5 单相与多相流场中各横截面的速度矢量图Figure 5 Speed vector－graph for multiphase flow and single－phase flow at different cross－sections

3 最佳转速和最小功率的分析

3.1 临界离底悬浮转速的分析

利用文献［8］中的浓度判据分析搅拌槽完全离底悬浮临界转速。其原理：单层球状固体颗粒堆积在一起时，固体颗粒体积分数若大于π／6（约52%）就说明固体颗粒没有完全悬浮，局部有堆积现象。即可以用局部固相体积分数的最大值φsmax作为完全离底悬浮的判据。

不同转速下槽底最大固相体积分数φsmax的模拟结果见图6。由图6可以看出此结构下临界悬浮转速Njs为635r／min。即当搅拌速度大于635r／min时，槽内达到完全离底悬浮状态。

3.2 最佳转速和搅拌最低功率的分析

基于CFD方法的搅拌功率的计算公式：

式中：

P—— 搅拌功率，W；

M—— 扭矩，N·m；

N—— 转速，r／min；

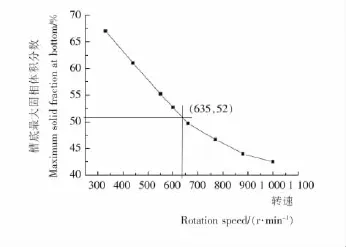
图6 不同转速下槽底最大固相体积分数φs maxFigure 6 Maximum solid volume fractionφs maxunder different rotation speeds at the tank bottom

ω—— 桨叶旋转角速度，rad／s。

对于三轴模型，扭矩为三轴扭矩之和，而各轴扭矩又包括搅拌桨扭矩Mi和搅拌轴扭矩Ms，即

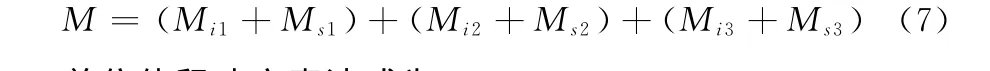
单位体积功率表达式为：

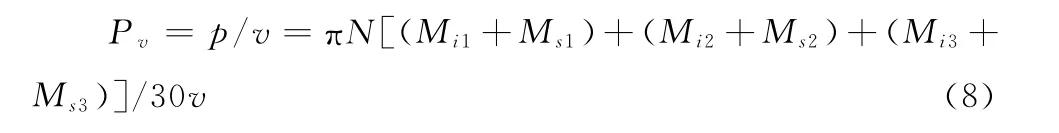
式中：

v—— 搅拌釜内固液流体体积，由体积公式v＝π（D／2）2HL求得v＝1.884m3。

由CFD结果得出各扭矩并计算单位体积功率和槽底平均固相浓度，具体数值见表1。

分析得出单位体积功率和槽底平均固相浓度随转速的变化具体情况见图7。

由图7可知，在相同的搅拌釜结构中，随着转速的增加，单位体积功率逐渐变大，即搅拌能耗逐渐变大；且此变化趋势成指数增加，即能耗随转速的提高比转速本身提高得更快。而槽底平均固相浓度则随着转速的增加逐渐变小，且其减小的速度没有转速增长的速度快。所以可以得出以下结论：转速越快，能耗越高，悬浮效果越好；转速越慢，能耗越低，悬浮效果越差。但为了改善悬浮效果，一味提高转速并不是最好的办法，因为转速增加到一定程度，随转速的提高，能耗增加得很快，而悬浮效果改善得较慢。所以根据此规律找出既能达到悬浮效果，又能消耗最低的功耗的最佳转速。

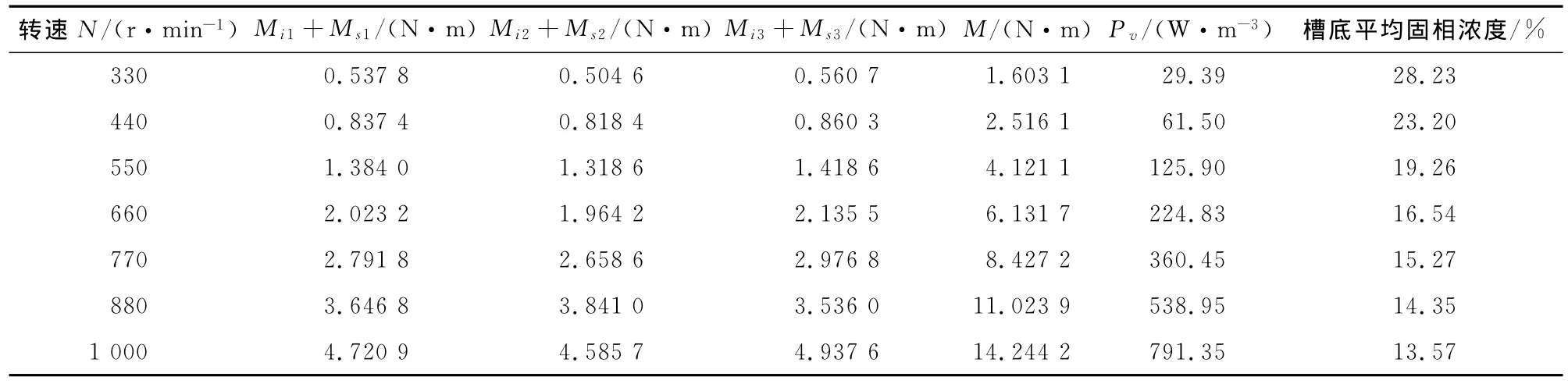
表1 不同转速下扭矩、单位体积功率及槽底平均固相浓度计算结果Table 1 The results of torquemoment，specific volume power and mean solidconcentration at bottom tank under different rotation speeds

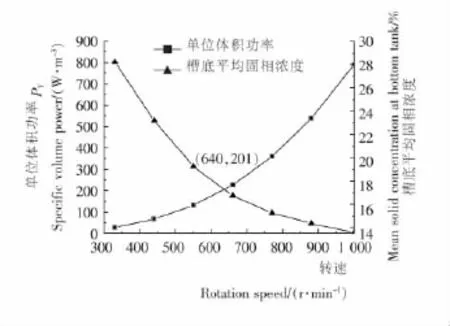
图7 单位体积功率和槽底平均固相浓度随转速的变化曲线图Figure 7 Variation trend of the specific volume power and mean solid concentration at bottom tank with the speed

综合上述结论和图7可知，两曲线的交点处，转速约为640r／min，略大于Njs，固此转速已能使搅拌槽中固相达到完全离底悬浮。所以可以选取此点转速作为搅拌时的最佳转速，此点的功耗作为最低的搅拌功率。即最佳转速为640r／min，最低搅拌功率为395.6W。

4 结论

用CFD数值模拟方法对立式多轴搅拌槽内固液悬浮性能进行研究，对槽内固体颗粒的分布规律进行分析，并讨论了不同转速对最大固相体积分数，单位体积功率和槽底平均固相浓度的影响，主要结论如下：

（1）利用CFD模拟预测的不同转速下槽底固相颗粒沉积带的形状和位置与试验结果相似，表现出较好的一致性；槽底中心和槽底两桨叶间靠近槽壁的区域易产生固相堆积，随着转速增加，沉积面积越来越小。

（2）对于单相体系，固体粒子的加入抑制了槽内轴向循环流的高度，且槽内液体总体速度明显降低。槽体上部流型为绕槽轴向的水平循环流，不利于槽内整体固相的均匀悬浮。

（3）在固含率为11%的槽内利用浓度判据，找出完全离底悬浮临界转速Njs为635r／min。

（4）利用CFD模拟并计算，分析得出单位体积功率和槽底平均固相浓度随转速的变化规律，找出既能达到悬浮效果，又能使功耗最小的最佳转速约为640r／min，此时所需最低搅拌功率为395.6W。

1 张少坤，尹侠.双层桨搅拌槽内流场的数值模拟［J］.食品与机械，2011，27（1）：71～73.

2 方键，桑芝富，杨全保.侧进式搅拌器三维流场的数值模拟［J］.石油机械，2009，37（1）：30～34.

3 陈道芳，徐雷兴，陈甘棠，等.固、液系机械搅拌槽中颗粒悬浮特性的研究［J］.化学反应工程与工艺，1992（3）：44～53.

4 银建中，程绍杰，贾凌云，等.搅拌式反应器内固－液两相悬浮特性的CFD模拟［J］.应用科技，2009，36（11）：11～16.

5 董厚生，魏化中，舒安庆，等.搅拌槽内固液两相流的数值模拟及功率计算［J］.化工装备技术，2012，33（1）：14～16.

6 李永纲，黄雄斌.立式圆槽内多轴搅拌器固－液悬浮性能［J］.过程工程学报，2012，12（2）：181～186.

7 刘冠一.侧入式搅拌中固液悬浮的数值模拟［D］.济南：山东大学，2010.

8 钟丽，黄雄斌，贾志刚.固－液搅拌槽内颗粒离底悬浮临界转速的CFD模拟［J］.北京化工大学学报，2003，30（6）：18～22.