基于分形理论的苏锡常城市群空间组织特征研究

崔大树，吴婷莉

(浙江财经学院经济与国际贸易学院，浙江 杭州 310018)

一、引 言

20世纪以来，随着经济全球化和区域经济一体化进程的加快，在经济发达的城市密集区出现了一种新的地域组织形式——城市群，并已成为要素集聚和经济发展的主要空间表现形式。我国已形成若干规模不等的城市群，其中以上海为中心的长江三角洲城市群被称为全球第六大城市群。苏锡常城市群是长江三角洲城市群的组成部分，位于长江三角洲的核心区域，是江苏省对外开放的前沿与先导、先进制造业与创新基地。苏锡常城市群空间效率的提升对长江三角洲城市群空间结构的优化和功能的增强以及加快江苏省的城市化进程发挥着重要作用。但进一步增强苏锡常城市群的空间协调性，整合苏锡常城市群的空间资源，尤其是如何优化苏锡常城市群的网络化空间结构，已成为目前进一步增强其空间功能的主要问题之一［1］。同时，行政区划与区域经济之间的冲突是苏锡常城市群空间优化过程中须解决的关键性矛盾［2］。针对这些问题，需要系统研究苏锡常城市群空间组织并进行定量分析，以准确认识其空间结构和功能的状态与过程。因此，我们运用分形理论分析苏锡常城市群的空间结构和功能。国外的相关研究主要以城市个体为对象，研究城市的形态、结构、生长、交通和演化机制等问题。Batty M.和Longley P.A.借助分形几何学研究了英国Cardiff城市的边界和形状、Swindon城市的土地利用形态等［3］［4］。国内的城市分形研究注重反映城市演化及其时空结构的一般规律，不仅对单个城市进行分析，也运用分形理论研究较大尺度城市群的空间问题。但很少有文献应用分形理论针对中等或较小尺度城市群的空间问题进行研究。我们尝试把分形理论与C-D函数结合起来分析苏锡常城市群的空间结构与功能，并在此基础上进一步研究该地区城市群的空间组织优化问题。

目前，城市群空间组织的概念在学术界还没有一个明确的定义，且往往与城市群空间结构的概念相混淆。国内许多学者则认为地域系统的空间组织是指该区域的城市规模、城市空间结构和功能等［5］。刘天东(2007)认为城市群的空间组织研究应当包括城市群的特征、功能、结构、等级体系等方面，并把城市群空间组织理解为“是通过一定的自组织法则和人类干预对城市内以及城市间各要素的组合和布局”［6］。为便于研究，我们认为城市群空间组织是城市群各要素在空间中的相互作用、形成的空间集聚程度和集聚形态(城市群空间结构)以及城市群内部结构和外部形态表现出的整体功能。

二、苏锡常城市群空间结构的分形特征

苏锡常城市群位于江苏省南部，区位比较优势明显，东依上海，南临太湖，是长三角城市群的重要一翼。汪淳和陈璐(2006)认为在苏锡常网络城市的构建中，苏州被定位为长江三角洲对外开放的前沿与先导和现代制造业与技术创新基地，无锡被定位为长江三角洲地区重要的先进制造业中心和现代物流中心，常州被定位为长江三角洲地区重要的现代制造业基地和区域中心城市［7］。苏锡常城市群以苏州、无锡、常州3个省辖市为核心，以所辖的9个县级市(苏州所辖的常熟市、张家港、昆山市、吴江市、太仓市，无锡所辖的江阴市、宜兴市，常州市所辖的溧阳市、金坛市)为主要经济腹地，依托沪宁铁路、沪宁高速、京杭大运河、苏嘉杭高速等促进经济要素的集聚和扩散，形成多核心的网络型城市地域系统。苏锡常城市群内部自然禀赋、地理因素都比较相似，历史文化、工业化进程、社会发展水平也都相近，从产业结构、空间结构(三核心)和城市功能来看，苏州、无锡、常州三市差异很小。各城市之间产业结构雷同，使城市群区域难以发挥整体的比较优势和规模经济效应，导致生产能力闲置和资源浪费，城市群的空间效率和系统性降低。苏锡常城市群空间效率的提升需要优化城市地域系统的空间结构和加强中心城市的功能整合，进一步突出节点城市之间的功能异质性和联系性。因此，揭示苏锡常城市群空间组织特征，以优化其空间结构和增强空间功能，已成为目前苏锡常城市群提升空间效率的主要问题。

描述分形的有效参数是分形维数，维数是反映空间现象的重要参量。在刻画城镇体系的空间结构方面，主要是通过三种分形维数(即聚集维数、网格维数和空间关联维数)进行分析［8］［9］。本文以上述三个维数为基础，结合具有分形特征的C-D函数，描述苏锡常城市群的空间组织特征。

(一)集聚维数:苏锡常城市群空间分布的向心性分形特征

式(2)中，Rs为平均半径，ri为第i个城镇到中心城镇的欧氏距离(即直线距离)，S为城镇个数，〈〉表示平均，式(3)中D为聚集维数。

式(4)中，ρ(r)为城镇体系的空间分布密度，一般取d=2。因此，当Df＜2时，Df－d＜0，城镇的要素分布从中心向四周密度递减;当Df=2时，Df－d=0，ρ(r)为常数，城镇体系的要素均匀分布;当Df＞2时，Df－d＞0，城镇体系的要素分布呈漏斗状，从中心城市向四周密度递增，这是一种非正常的情况。根据上述集聚维数分形模型，分别以苏州、无锡和常州为中心城市，量取各城市到中心城市的空间距离(以欧式距离为准)，通过式(2)计算得出平均半径(见表1所示)。

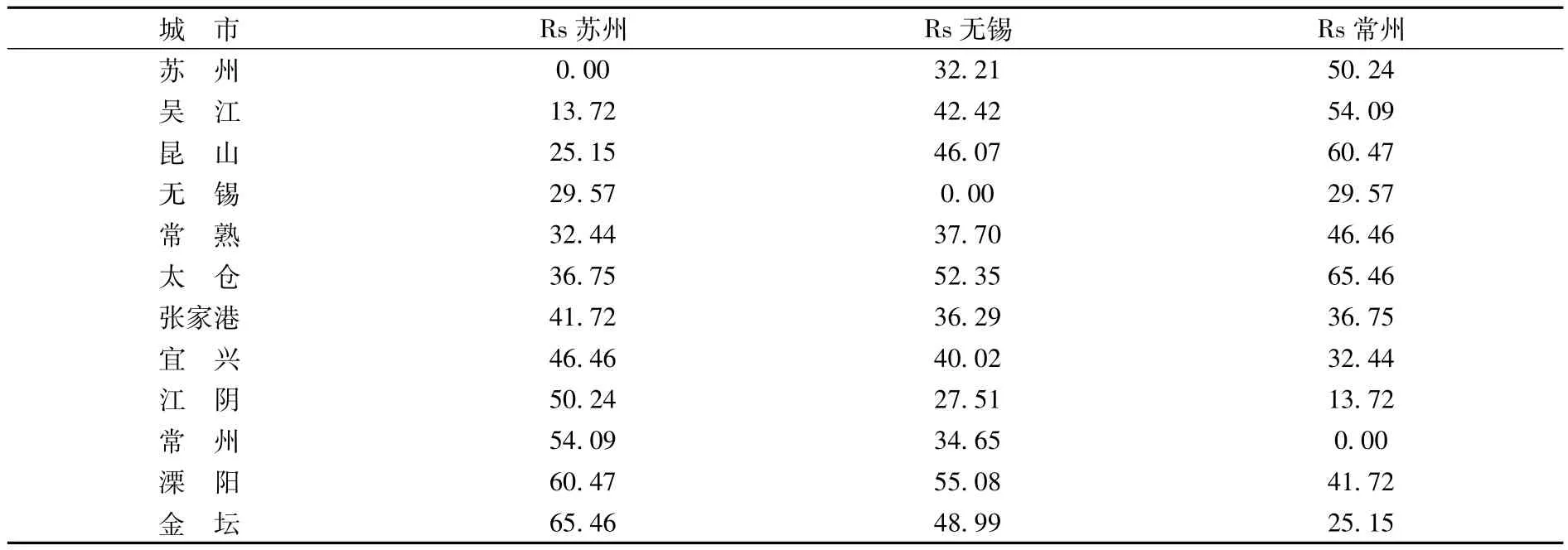
表1 以苏州、无锡、常州为中心的集聚维数测算数据 单位:公里

在EXCEL中，以lnS为横坐标、lnRs为纵坐标做散点图，可见存在明显的无标度区，即说明存在分形特征。再对无标度区范围进行回归，可以得到x(也就是lnS)的系数即为集聚维数(见图1所示)，图中仅标识了无标度区的数据。图1显示，以苏州为中心城市、其余11个城市为腹地的集聚函数为lnRs=0.6917lnS+2.411，集聚维数 D=1/0.6917=1.4457，测定系数R2=0.9865;以无锡为中心城市的城市群的集聚函数为lnRs=0.6076lnS+2.4964，集聚维数D=1/0.6076=1.6458，测定系数R2=0.9959;以常州为中心城市的城市群lnRs=0.625lnS+2.6434，集聚维数D=1/0.625=1.6，测定系数R2=0.9861。三个集聚维数都小于2，说明在苏锡常城市群中，三个核心城市都具有一定的集聚性，分别向着三个核心城市聚集，并且从中心城市向周围地区分布的密度递减。但由于三个集聚系数都接近于2且相差无几，说明这三个地区的集聚能力相近，只有苏州表现的较为突出，说明苏锡常地区空间集聚的特点不明显。

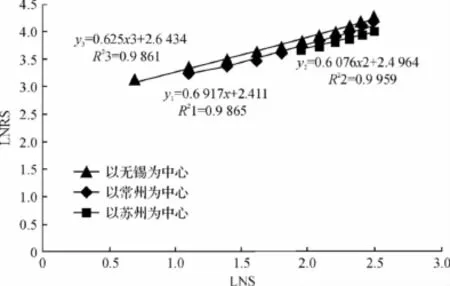
图1 苏锡常三市随机集聚分布

(二)网格维数:苏锡常城市群空间结构的均衡性分形特征

对研究区域进行网格化处理，每个网格的边长都是ε，考察在所有的网格中拥有城镇的网格数为N=(ε)，N(ε)会随ε而变化。若城镇的分布体现无标度性，则应有:

表2 标度K下的N和I值

根据形成的 I(ε)－ln(ε)的散点图，对其无标度区进行线性回归，可得方程式 I(ε)=0.9095lnK+0.7954，信息维D=0.9095，测定系数R2=0.9493，拟合度良好，网格维数接近1，说明苏锡常地区的城市分布较为均衡，表现出较为明显的围绕某一条线分布的特点，我们认为该“线”就是太湖的岸线。

(三)关联维数:苏锡常城市群空间结构相关性的分形特征

一般地，城镇体系的空间关联函数为:

式(8)中，r是距离标度，dij为城市i和城市j两城镇的欧氏距离(即直线距离)，θ为Heaviside函数，它具有如下的性质:

对比豪斯多夫维数，式(11)中的α=D是空间关联维数，其地理意义反映了城镇间的空间关联性。与网格维数相似，其数值介于0－2之间，其值越大，表征区域内城镇空间分布越分散;其值越小，表征区域内城镇空间分布的集中度越高，空间关联越紧密。当D→0时，表明城镇分布高度集中于一地;当D→2时，表明城镇的空间分布较为分散。而空间关联维数的独特用途在于可以反映城镇体系各要素之间交通网络的通达性，用基于交通的乳牛距离测算得到的维数D'与基于直线距离求得的维数D之比来表征通达性的强弱。

根据地图测得苏锡常城市群区域12个主要城市之间的直线距离，表现为一个对称矩阵，这里只标注右上角的数据，左下角的数据与之相同，此处略去，单位取公里。再以△r=10作为距离标度r，统计出在距离r之间的分形点数Nr，随着r的变化而变化，我们就可以得到一系列点(r，Nr)(见表3所示)。

表3 在标度r下的Nr值

以lnr为横坐标、lnNr为纵坐标做出散点图，针对图中的无标度区进行线性回归，我们可以得到苏锡常城市群的关联维数D=1.1648，关联维数在1－2之间，说明各城市之间有较强的空间关联性，主要体现在苏锡常各地区间的紧密合作和依赖性。

(四)功能模型:C-D函数及苏锡常城市群空间功能的强化

分形是大自然中的优化，分形体能最有效地利用地理空间。由于城市体系中任何要素对于该体系的输出都会有一定的贡献，因而我们可假设城市地理系统要素pi的某种侧度xi与产出y之间的数理关系如下:

核心城市的要素在城市群发展的不同阶段会发挥出相应的功能。通常表示城市要素的常用变量是人口和用地，二者分别取反映要素的苏州市区、无锡市区和常州市区近几年的非农业人口数(P)和建设用地面积(S)以及反映产量的工业总产值(Y)为测度。

以统计年鉴中的市区非农业人口、市区建设用地面积和市区规模以上工业总产值，将非农业人口-工业总产值和建设用地面积-工业总产值的数据整合成幂函数曲线，我们可以发现苏州市人口-产值的关系为 Y=0.0001P3.4279，建设用地-产值的关系是 Y=0.7402S1.5739，二者综合为 Y=0.0086P1.71395S0.78685。因此，人口维数是1.71395，土地维数是0.78685。无锡市的人口维数为σ1=1.0216，土地维数是σ2=2.2403。常州市的人口维数是σ1=2.93155，土地维数是σ2=1.80085。从以上数据可以看出，苏州和常州的人口维数比土地维数大，从城市经济发展的角度看，说明人口带来的经济效益比土地更大。因此，苏州市和常州市的人口要素相对土地要素而言功能更强，未来的规模增长可以以引进优质人才为主，而不宜过快地扩大建设用地。无锡则是土地维数大于人口维数，说明无锡市土地要素的功能强于人口要素，应该加强该市的土地规划，适当扩大建设用地，以此带动其他要素功能的发挥。

基于前述的C-D模型，我们可以得出城市系统结构与功能优化的分维关系［10］。该优化过程可以类比经济学中的成本最小化和利润最大化，无疑是在xi(i=1，2，…，n)一定的情况下使y值最大，或是在y值一定的情况下使xi值最小。运用类似的方法，我们可以得到方程组:

式(15)中，wi为要素pi的广义价格，C0为要素投入的最大值。利用拉格朗日乘数法则，我们可将上式简化为:

三、主要结论及政策含义

通过以上的分析，我们主要得出以下基本结论:

第一，从苏锡常城市群空间结构的分型特征来看，该区域有三个中心城市——苏州、无锡和常州，且集聚程度相似，不存在首位城市，没有明显的增长极。一方面，该区域会形成过度竞争，难以发挥中心城市的集聚和辐射作用;另一方面，苏锡常城市群具有明显的自相似结构。通过集聚维数、网格维数和关联维数的测算，苏锡常城市群主要趋向苏州、无锡、常州三个城市集聚，分布较为均衡，最终形成一个以太湖为基点的扇形区域。同时，集聚密度分别从三个中心城市向四周分布递减，但相互间关联密切，其主要原因是依托便利的交通干线，形成典型的网络型城市群空间结构。

第二，我们把分维思想与C-D函数的检验结合起来，并通过城市系统的多要素产出关系分析了苏锡常城市群的要素功能强弱表现。研究结果发现，苏州和常州市的人口要素功能大于土地要素，其经济效益大于土地经济效益，而无锡则相反。因此，苏州和常州市在经济和社会发展建设过程中，可以加大对人才的培养和利用，而无锡则应更加注重对土地利用的规划与管理，合理有效的开发利用土地资源。

第三，从苏州、无锡、常州三市的要素功能来看，苏州和常州市的要素功能基本一致，表现为人口功能强于土地功能。三市的整体功能也相似，职能分工差异化较小。苏锡常具有相似的区位、资源等自然禀赋条件，产业结构趋同。在有限的积聚空间内，产业结构趋同导致同类产品过剩和过度的市场竞争，造成各城市在同一层次上的重复建设，使整体聚集效益下降。相似的产业结构造成了相似的城市功能，苏锡常城市群就形成明显的主导功能不明确，限制了比较优势的发挥。针对这些问题，应进一步优化苏锡常城市群的空间结构，在此基础上加强专业化生产和区域分工，使各城市发挥具有自己优势的特色功能和确定各自主导功能，并通过主导功能的相互渗透进行区域合作与分工协作。同时，建立协调机构，构建苏锡常网络城市，提升苏锡常城市群国际竞争力，更好地增强整体功能效益，实现苏锡常城市群经济、社会和环境可持续发展。

［1］陶闽齐，曹国华.培育苏锡常都市圈网络化空间结构［J］.城市规划汇刊，2003，(2):44－50.

［2］顾松年.苏南现代化与区域一体化——兼探苏锡常怎样“圈”起来［J］.现代经济探讨，2003，(1):11－13.

［3］Batty M.，LongleyBP.A.Fractal Cities:A Geometry of Form and Function ［M］.London:Academic Press，1994.

［4］Batty M.Cellular Automata and Urban Form:A prime［J］.Journal of the American Planning Association，1997，63(2):266－274.

［5］聂华林，王成勇.区域经济学通论［M］.北京:中国社会科学出版社，2006.

［6］刘天东.城际交通引导下的城市群空间组织研究［D］.中南大学博士学位论文，2007.

［7］汪淳，陈璐.基于网络城市理念的城市群布局——以苏锡常城市群为例 ［J］.长江流域资源与环境，2006，15(6):797－800.

［8］刘继生，陈彦光.城镇体系空间结构的分形维数及其测算方法［J］.地理研究，1999，18(2):171－178.

［9］刘继生，陈涛.东北地区城市体系空间结构的分形研究［J］.地理科学，1995，15(2):136－143.

［10］陈彦光.城市地理系统结构与功能的分形模型——关于地理系统异速生长方程与Cobb-Douglas函数的理论探讨与实证分析［J］.北京大学学报，2003，39(2):229－235.

［11］陈彦光，罗静.经济系统结构与功能的分形模型——Cobb-Douglas生产函数的理论来源及形式推广 ［J］.信阳师范学院学报，2000，13(1):40－43.