基于决策函数及PSO优化的SVM预测控制应用研究

王 杰，陈锴鹏

(郑州大学电气工程学院，河南郑州450001)

0 引言

预测控制因其对模型的精度和表达形式要求不高而受到了广泛关注，但是在面临非线性控制对象时存在着模型失配、鲁棒性差的问题.因此研究和改进非线性预测控制是一个非常有意义的课题［1］.

支持向量机(Support Vector Machine，SVM)在解决非线性问题上与其它算法相比有泛化能力强、鲁棒性好等优点［2］.但是LeCun等人的在研究大规模样本回归时发现，SVM训练的速度要明显慢于同等精度的神经网络［3］.为了提高SVM的训练速度，笔者提出了一种基于简化决策函数的SVM预测控制器，采用SVM对非线性对象进行回归建模，并通过矩阵变换对SVM的支持向量进行约简，加快了模型训练速度，将对象的SVM模型作为预测控制中的预测模型，通过粒子群算法(Particle Swarm Optimization，PSO)来确定 SVM的最优参数和对预测控制的最优控制律进行滚动优化［4］.

1 SVM预测模型

1.1 决策函数约简的SVM回归问题

s.t.yi(〈φ ( xi)，w〉+b )≥1 － ξi，ξi≥0，i∈ N构造决策函数K(·， ·)是将样本向量映射至高维空间的核函数.根据基础线性代数理论，可以证明支持向量x(k)在特征空间Z中与其它支持向量是线性相关的，即有为标量常数.则决策函数的表达式可以写成如下形式：

已知线性相关的向量可以用其它向量表示，因此，在表述决策函数的时候线性相关的支持向量是不需要的.所以，我们可以对支持向量进行消减来简化决策函数.采取行阶次消减的的形式来对决策函数进行简化［6］.

研究过程中发现，仅仅通过矩阵线性变换来约简决策函数，效果不太明显，为了提高简化的效果，引入松弛变量Γ，在通过矩阵变换寻找依赖关系的时候，如果某一行的元素值全部小于Γ，则该样本点对应的支持向量可以删除.合理选择松弛因子的大小，使得训练误差在可以接受的范围内实现决策函数的最简化.由于决策函数复杂度降低，训练的速度得到了明显提升.

1.2 PSO优化SVM参数

采用Lagrange乘数法解决上述约束问题

式中：α为拉格朗日乘子.根据最优性条件可以得到原问题的对偶问题：

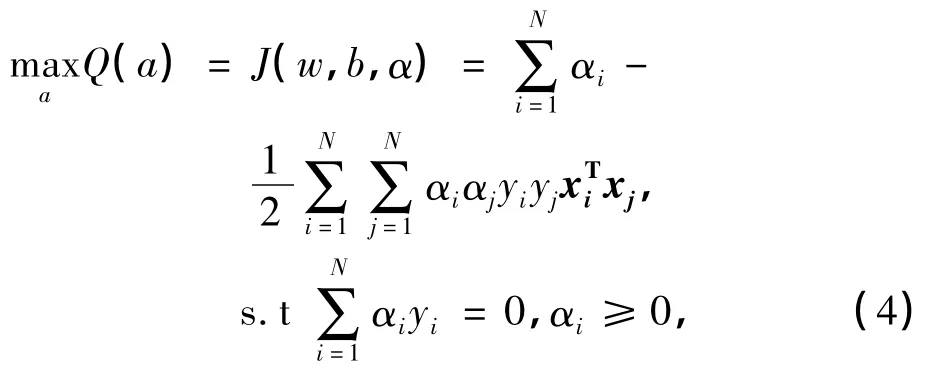
公式(4)问题的求解通过训练数据集得到.

如何选取最佳的SVM参数，国际上还未出现一个公认的最好方法，目前所用的方法是让c和g在一定范围内取值，利用训练数据来测试分类准确率，利用分类准确率来确定c和g的值［7］.如果遇到多组最优的c和g，则采取c值最小的一组数据.这样可以避免c值过大引起的过学习情况.为了得到最佳的SVM参数，笔者采用PSO算法对SVM的惩罚参数c、不敏感损失系数g及核函数σ参数进行优化，最终得到的SVM模型表达式为：

1.3 SVM模型线性化处理

为使广义预测控制器能够作用于SVM非线性模型，对式(5)进行线性化处理：对第k个采样周期，xk是相应的回归向量，取式(5)在xk处泰勒展开式，得到线性化模型［8］：

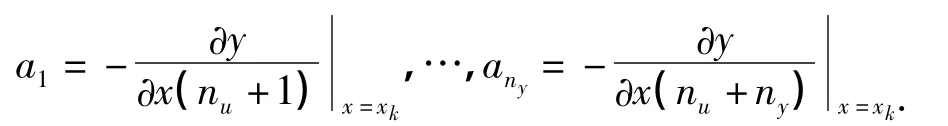
取回归向量：x(k)=［xk(1)…xk(nu+ny)］=［u(k－1)…u(k－nu)y(k－1)…y(k－ny)］

令n=nu+ny，选取RBF核函数，式(6)可写为

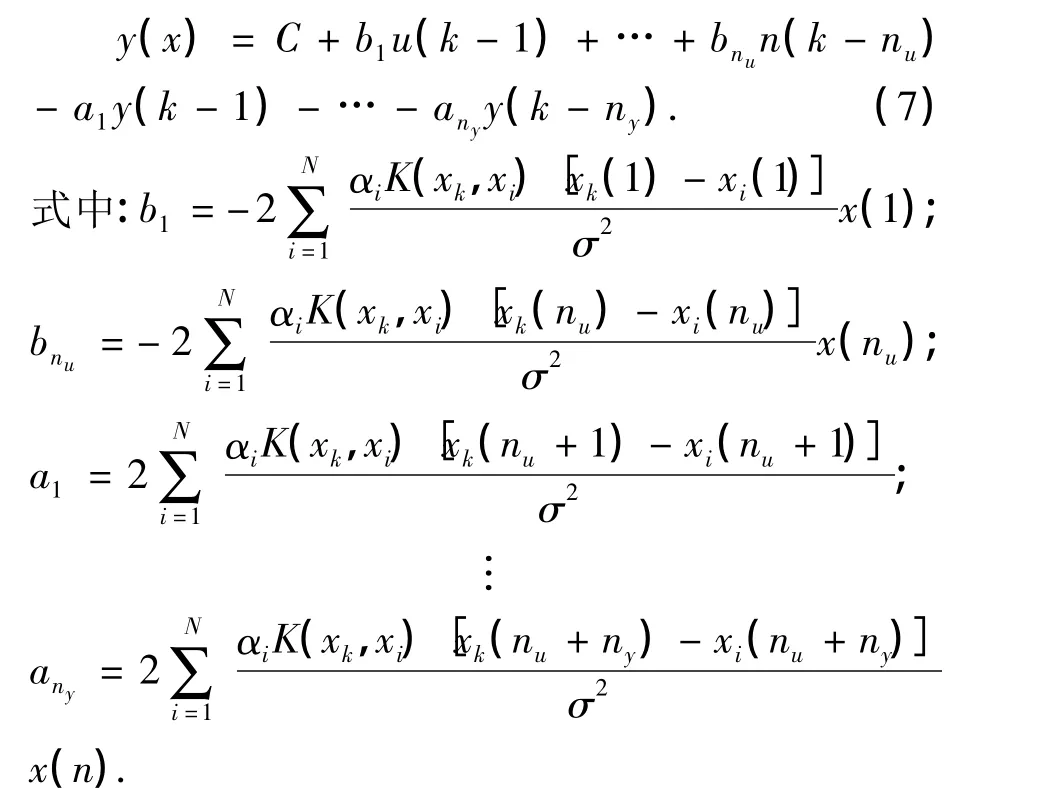
式(7)可作为预测控制的预测模型.

2 PSO滚动优化的预测控制

预测控制的任务就是使系统输出y(t+j)尽可能逼近输出设定值yr(t+j).性能指标函数如下［9］：

式中：E{·}表示取数学期望，一般工业过程中最终输出设定值为常值c，为了使输出平稳，令yr(k+j)=αjy(k)+(1－αj)c，α∈［0，1)为柔化因子;N1和N2分别为优化时域的起始与终止时刻;nu为控制时域［10］.为了计算预测控制器的控制律，采用粒子群算法进行迭代计算.

设定待优化的控制量u(k+1)为PSO算法中的位置向量，SVM预测输出量为yM(k+j+1)，系统实际的输出量和预测输出量之间的偏差为e(k+j)=y(k+j)－yM(k+j)，误差修正后估计输出为yP(k+j+1)=yM(k+j+1)+e(k+j).PSO适应度函数选取为预测控制的性能指标函数.输出gbest为最优控制量u(k+1).粒子更新的公式为［11］

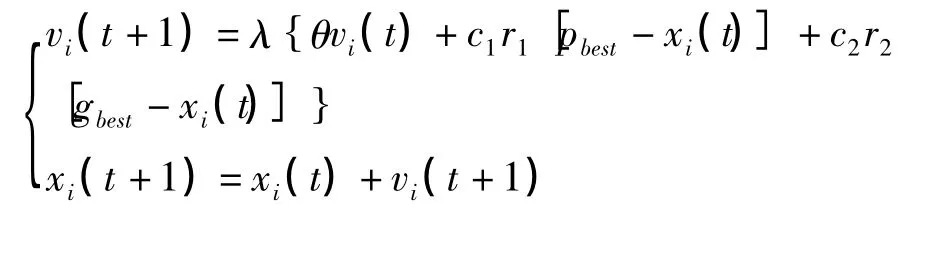
式中：θini和θend为惯性权重的初始值和终值，c1和c2为学习因子，m为最大迭代次数.惯性权重的大小代表算法的全局和局部的搜索能力.学习因子c1和c2反映了粒子群之间的信息交流［12］.

3 算法流程

基于以上算法的描述及分析，笔者算法流程如图1所示.

图1 笔者算法流程图Fig.1 Algorithm flow chart this paper proposed

4 仿真研究

4.1 SVM决策函数约简数学仿真

为了验证决策函数约简对支持向量个数减少的效果，我们采用kinfamily数据库中的4 000个数据点来进行验证，简化后的结果如表1所示.

4.2 回转窑数据预测控制仿真

为验证笔者方法在实际工业过程中的有效性，以水泥回转窑窑尾烟室温度模型为控制对象进行控制仿真.选取分解炉出口温度、预燃室下部温度、入窑二次风温、五级筒出口温度和窑尾烟室温度历史值5个变量为输入量，输出量为窑尾烟室温度.数据采样间隔为每分钟采样一次，选取水泥回转窑连续正常工作3 d时5 000组数据作为实验数据，前4 000组用来建模，后1 000组用来测试.采取PSO算法来确定SVM的参数，Cbest=86.301 8，gbest=0.01模型的预测误差由图2所示.

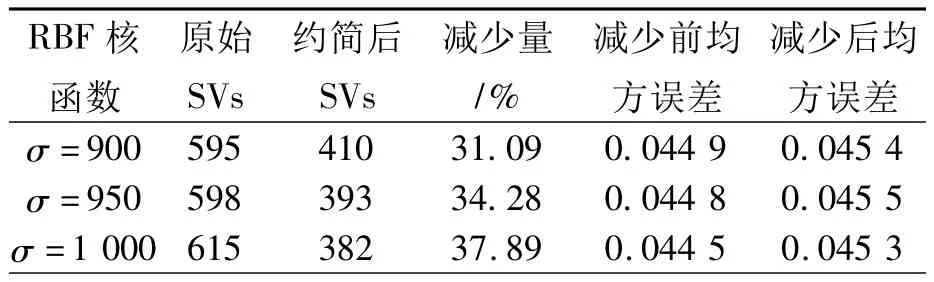
表1 RBF核函数SVM决策函数简化结果Tab.1 Results of SVM decision functions simplification using RBF kernels

图2 SVM建模误差Fig.2 modeling error rate of SVM

由图2可以看出LSSVM建立的模型误差基本在－0.05～+0.05之间.根据相关工艺经验，窑尾烟室的最佳温度为1 200℃左右.因此设定期望输出值c=1 200，优化时域为N2－N1=10，控制时域nu=5，μ=0.9，PSO算法中粒子数m=10，θ=0.5 最大迭代次数为 200，c1=1.6 ，c2=1.5.系统响应图为图3.从图3中可以看出在对回转窑窑尾烟室温度模型的控制过程当中，笔者所采用的方法能够有效地减少系统的超调量，加快了系统的响应速度.

图3 笔者方法与传统GPC控制效果对比Fig.3 Control effect of GPC and method we proposed

5 结论

采取对决策函数进行约简的方式来对SVM进行改进，实验数据表明这种方法能够在不影响模型精度的情况下有效地减少SVM的支持向量个数.广义预测控制具有对模型精度要求不高的特性，因此约简后的模型精度上完全满足预测模型的精度要求，实现了广义预测控制对非线性模型的控制.通过对水泥回转窑窑尾烟室温度模型的仿真结果上表明该算法在实际工业过程中的适用性.

［1］席裕庚.预测控制［M］.北京：国防工业出版社，1993.

［2］VAPNIK V N.Statistical Learning Theory［M］.New York：Wiley，1998.

［3］LECUN Y，JACKEL L，BOTTOU L.Comparision of learning algorithms for handwritten digit recognition［C］//International Conference on Artificial Neural Networks.P.Gallinari，1995.

［4］肖本贤，朱志国，刘一福.基于粒子群算法混合优化的广义预测控制器研究［J］.系统仿真学报，2007，19(4)：820 －824.

［5］COLLOBERT R，BENGIC S.SVMTorch：Support vector machines for large-scale regression problems［J］.Journal of Machine Learning Research.2001(1)：143 －160.

［6］TOM D，KEVIN E G，ANNETTE M.Exact Simplification of support vector solutions［J］.Journal of Machine Learning Research，2001(2)：293 －297.

［7］姜谙男.基于PSO－SVM非线性时序模型的隧洞围岩变形预报［J］.岩土力学，2007，27(6)：1176－1179.

［8］LUCH T C C.Generalized predictive control using recurrent fuzzy neural networks for industrial processes［J］.Journal of Process Control，2007，17(1)：83－92.

［9］ALFI A.PSO with Adaptive mutation and inertia weight and its application in parameter estimation of dynamic systems［J］.Acta Automatica Sinica，2011，37(5)：541－549.

［10］郭巧，曹海璐.一种改进的广义预测控制方法及其应用［J］.控制理论与应用，2001，18(2)：310－313.

［11］穆朝絮，张瑞民，孙长银.基于粒子群优化的非线性系统最小二乘支持向量机预测控制方法［J］.控制理论与应用.2010，27(2)：164－168.

［12］贾嵘，洪刚，薛建辉，等.粒子群优化－最小二乘支持向量机算法在高压断路器机械故障诊断中的应用［J］.电网技术.2010，34(3)：197 －200.