变压器励磁涌流及其对差动保护影响的仿真分析

王 慧，闫 坤，高厚磊，陈学伟

（山东大学 电气工程学院，山东 济南 250061）

电力变压器是电力系统中不可缺少的重要电气设备，变压器故障将对供电可靠性和系统安全运行产生严重影响。变压器一般采用电流差动保护作为主保护，其理论依据是基尔霍夫电流定律。但是，由于变压器内部磁路的联系，其励磁回路相当于变压器内部故障的故障支路，变压器励磁电流成为差动保护不平衡电流的主要来源之一[1－2]。

在继电保护设计或教学中，变压器励磁涌流的产生机理、对差动保护的影响以及解决方法是重点内容，也是难点内容。为了更形象地说明变压器励磁涌流及其对差动保护的影响，有利于学生对抽象概念和理论的理解，本文借助电力系统暂态仿真工具PSCAD建立变压器仿真模型，真实反映励磁涌流的特征和变压器的不同故障状态；采用Matlab编写变压器差动保护程序，采用VC编写仿真界面，实现基于数字仿真的变压器励磁涌流及其对差动保护影响的教学方案[3]。

1 变压器的励磁涌流

励磁涌流的大小取决于变压器铁芯的饱和程度。变压器在正常运行和外部故障时，铁芯不会饱和，励磁电流不会超过额定电流的2%～5%。当变压器空载投入或外部故障切除后电压恢复时，变压器的电压从零或很小的数值突然上升到运行电压。在这一暂态过程中，变压器铁芯可能会严重饱和，产生很大的暂态励磁电流，该电流被称为励磁涌流。

励磁涌流的最大值可达变压器额定电流4～8倍，并且与变压器的额定容量有关。大型变压器的励磁涌流与额定电流的比值会小一些，但也在3倍左右。如此大的励磁涌流如果通过提高整定电流来躲过，将造成保护灵敏度的严重下降，使短路电流不是很大的情况下无法正确动作。所以，变压器差动保护中常采取措施识别励磁涌流并闭锁差动继电器以防止保护误动[4]。

2 励磁涌流的特征

2.1 基于PSCAD的变压器模型的建立

按照变压器差动保护的需要搭建了双端供电系统模型，如图1所示。两侧电源使用两个不同电压等级的交流电压源模拟。变压器选用SFP10-160000／220W3型，主要参数为：额定容量SN＝160000kVA；额定电压UN＝242±2×2.5%／13.8kV；连接组别为YNd11；短路阻抗Ud＝13.31%，空载损耗P0＝900 kW，短路损耗为Pk＝2400kW。

2.2 励磁涌流特征仿真

为了使变压器差动保护不会因为空载投入或区外故障切除电压恢复时产生的涌流而误动，必须准确识别涌流并将保护闭锁[5－6]。为此，需要对变压器励磁涌流波形的典型特征进行研究。以A相为例，分别选择0°、30°、60°、90°、120°、150°作为合闸角进行空载合闸仿真，仿真结果如图2所示。

对仿真的涌流波形进行了谐波含量分析，所得结果如表1所示。

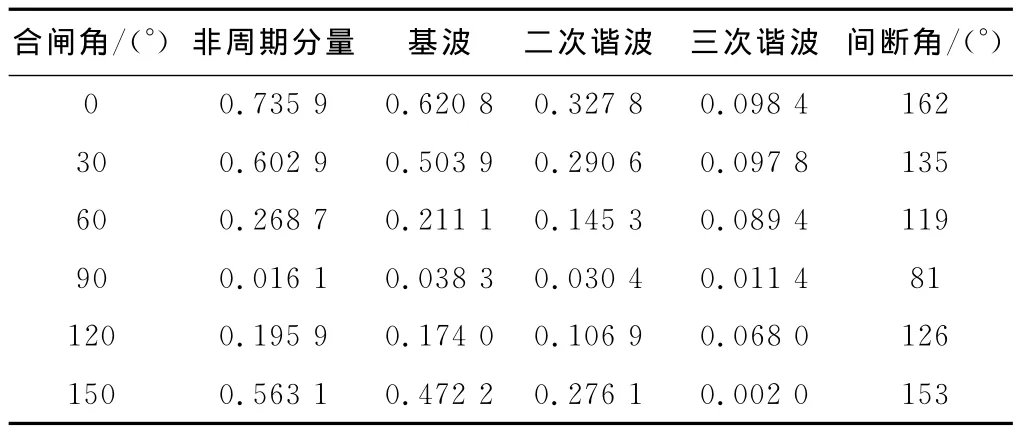
表1 不同合闸角时励磁涌流谐波及间断角

从以上仿真结果可以看出：

（1）变压器空载投入时，由于铁芯饱和，出现了励磁涌流，且涌流的大小与合闸角有关。合闸角α＝0°时涌流最大，α＝90°时涌流最小。

（2）除基波外，涌流中还含有非周期分量和高次谐波分量。合闸角为0°～90°时，非周期分量和三次谐波幅值随合闸角增大而减小；合闸角为90°～180°时，非周期分量和三次谐波幅值随合闸角增大而增大；合闸角α＝90°时，非周期分量和三次谐波幅值最小，此时基本无合闸暂态。

（3）励磁涌流中含有显著的二次谐波分量。合闸角为0°～90°时，二次谐波含量随合闸角的增大而减小；合闸角90°～180°时，二次谐波含量随合闸角的增大而增大；合闸角α＝90°时，二次谐波含量最小。

（4）涌流波形在最初几个周期内完全偏于时间轴的一侧，且有明显的间断角。合闸角为0°～90°时，间断角随合闸角的增大而减小；合闸角为90°～180°时，间断角随合闸角的增大而增大；合闸角α＝90°时，间断角最小，此时出现对称涌流。

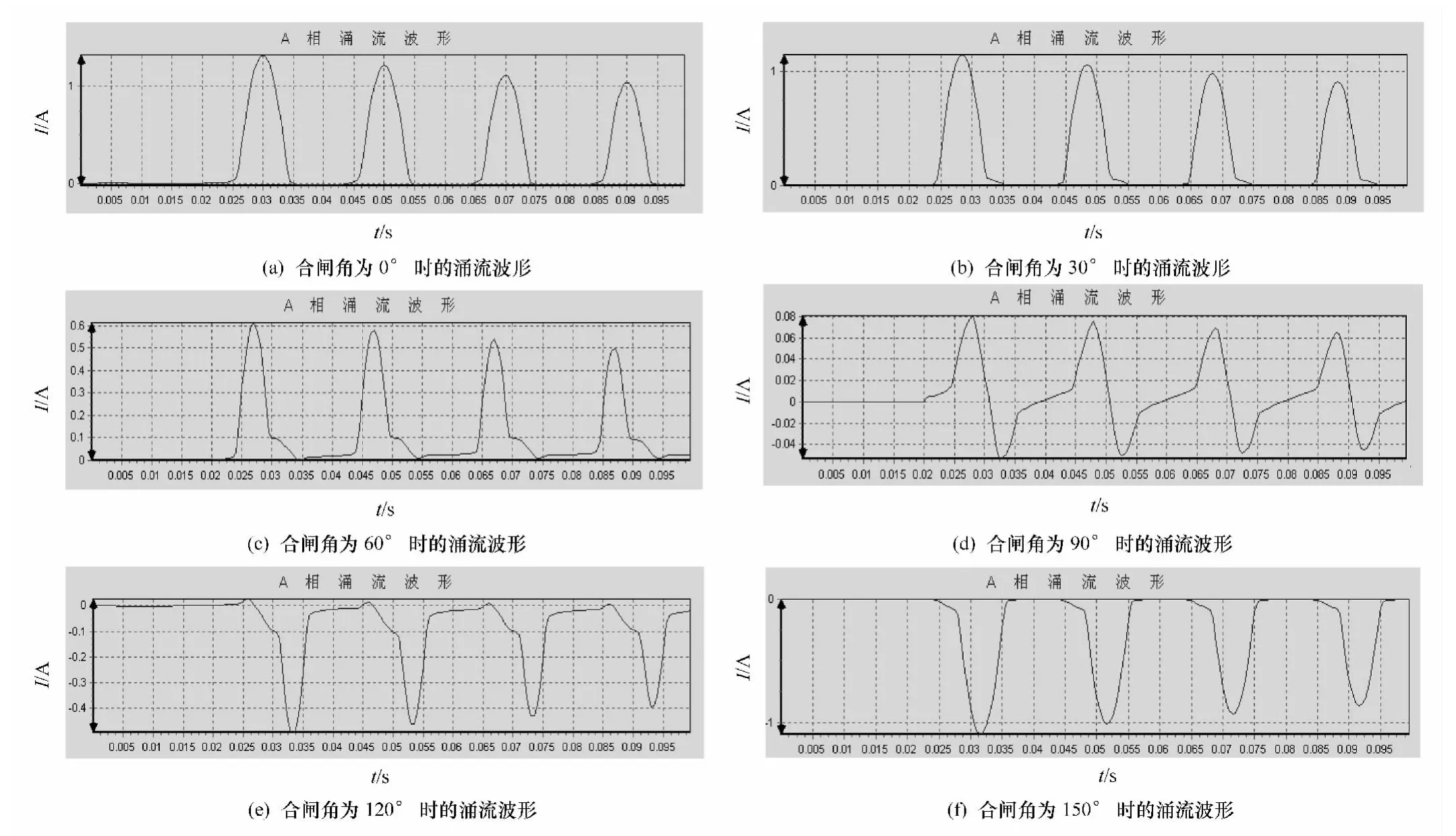
图2 不同合闸角时的涌流波形

2.3 相位和幅值的调整

由于变压器通常采用Y／Δ接线，三角形与星形侧CT二次电流相位相差30°，所以在差动保护计算前需进行电流相位调整，使纵差保护由变压器两侧取得的电流相位相同。调整后的涌流波形见图3。

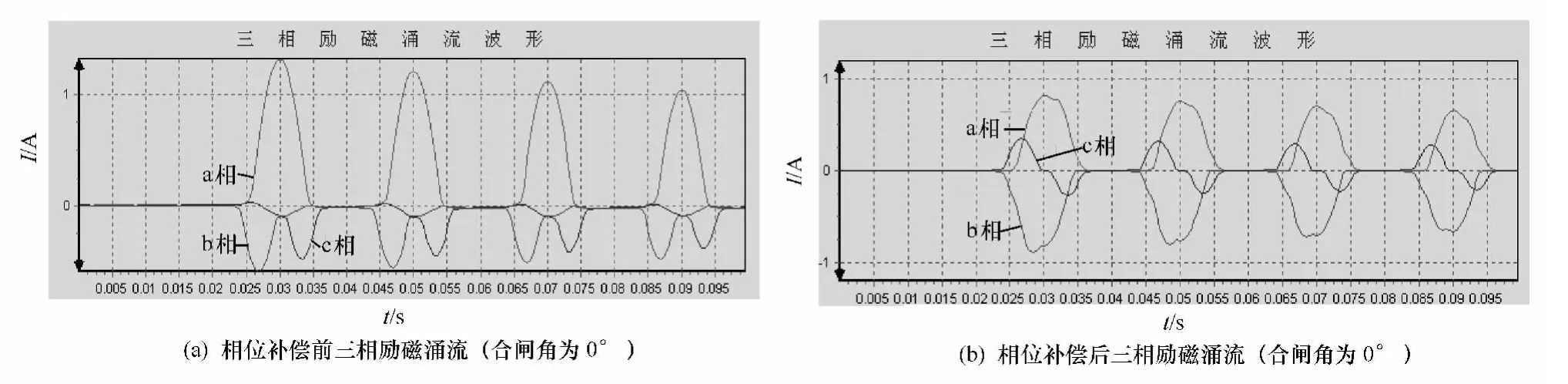
图3 相位补偿前后三相励磁涌流

通过图3（a）、图3（b）对比可以看出，经过相角和幅值调整后，流经差动继电器的励磁涌流与实际变压器各相绕组中流过的励磁涌流在波形特征上有很大差别。经相位调整后会出现对称性涌流，而对称性涌流中二次谐波含量会比较低，出现对称性涌流的一相将很难识别出涌流。

3 影响励磁涌流的因素

励磁涌流的大小和铁心饱和程度、铁心的剩磁、合闸时电压的相角等因素有关。本文主要讨论合闸角和剩磁对励磁涌流的影响。其中合闸角的影响在2.2节已经分析，这里不再赘述。

为了分析铁芯剩磁对励磁涌流的影响，可通过设置直流电源来模拟剩磁。要想模拟出不同剩磁的影响，关键是找到加在变压器上的直流电流与其在变压器中产生磁通的关系。仿真模型如图4所示。

通过仿真实验得到的外加直流源与铁芯剩磁的关系如表2所示。

表2 直流源与剩磁的关系

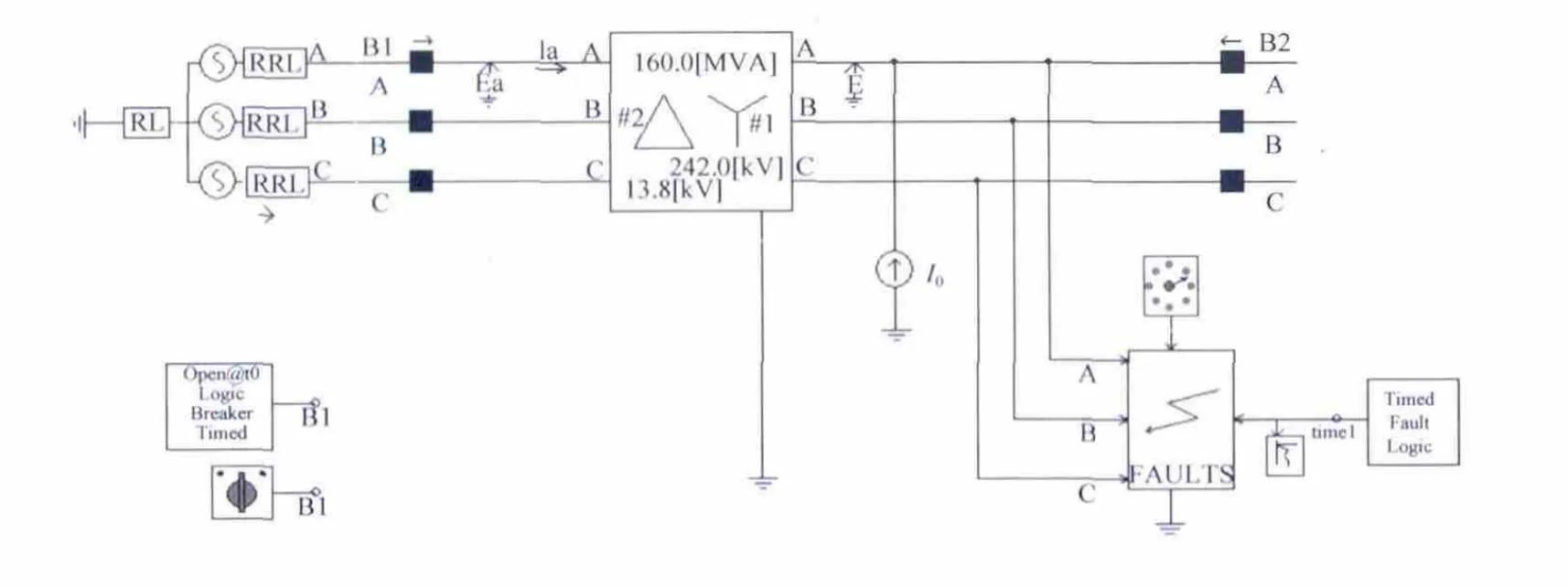
图4 剩磁对励磁涌流的影响仿真模型

图5所示分别为a相剩磁0、0.3、0.7、1时三相励磁涌流波形（合闸角90°）。

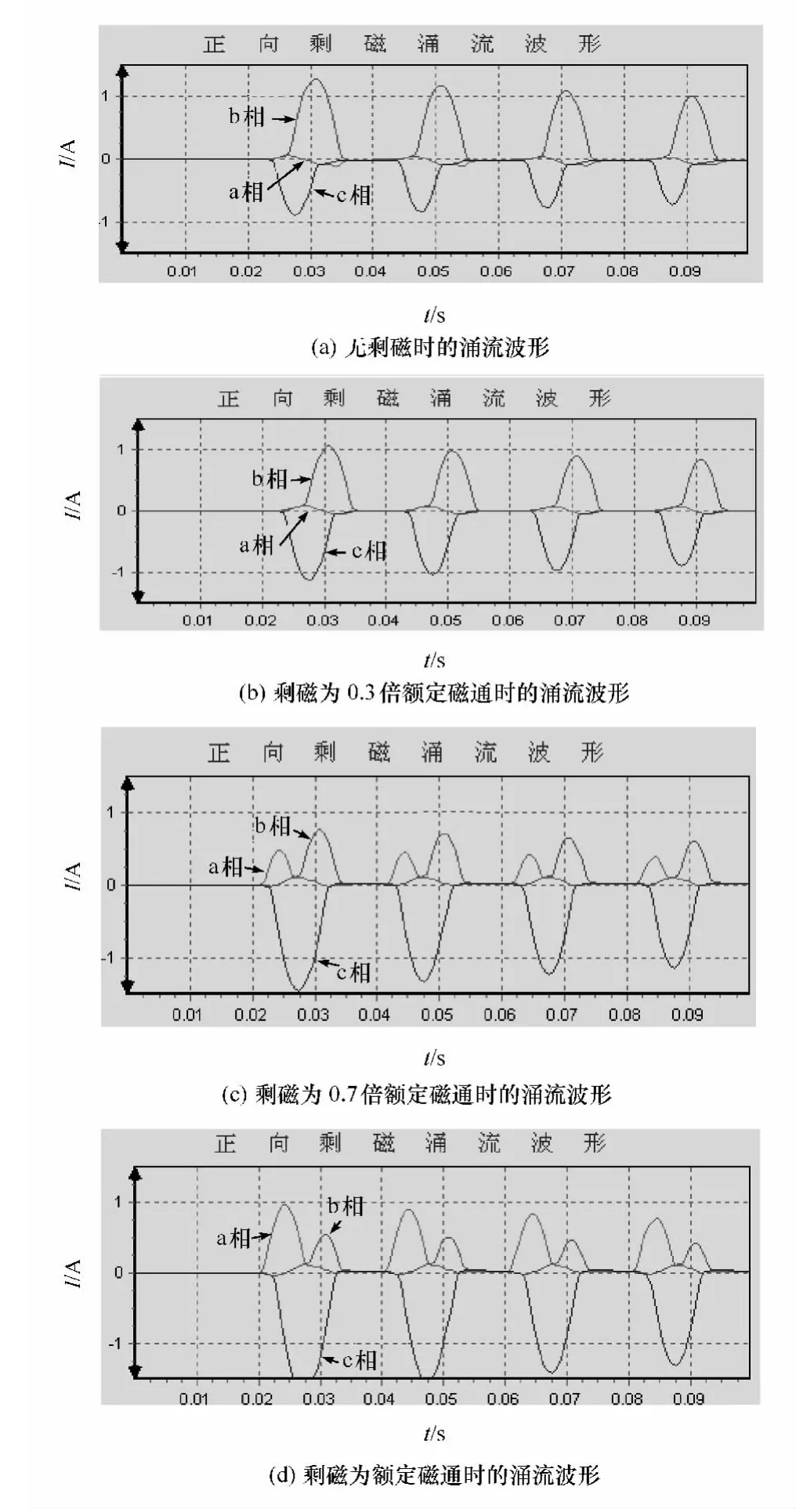
图5 不同剩磁时的涌流波形

由图5可以看出，在a相加上正相剩磁，a相励磁涌流随着剩磁的增加越来越严重，说明正相的剩磁对正向涌流起了助长作用；由b相的涌流波形可以看出，反相剩磁对正向涌流起抵消作用；同理，c相涌流波形说明反向剩磁对反向涌流起助长作用。

4 励磁涌流对差动保护的影响分析

4.1 励磁涌流的识别及保护闭锁方案

常用的励磁涌流识别原理有间断角原理、二次谐波制动原理、波形对称原理。由于二次谐波制动原理简单，一直被广泛地应用。

为提高保护的可靠性，二次谐波制动的励磁涌流闭锁判据最好采用全相闭锁的方式。全相闭锁可以采用两种形式：一种是采用三相中二次谐波比最大的相闭锁，但可能存在带轻微故障合闸时动作速度慢的不足；另一种是采用选取三相中二次谐波最大值、基波最大值作比的方式，它在动作可靠性和速度上达到较好的平衡。无论经哪种电流相位的调整，均具有较高的稳定性[7－9]。本文采用第二种方式进行仿真。

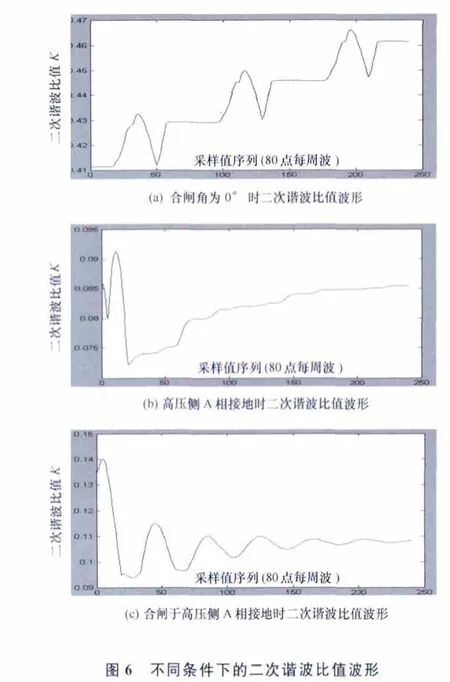
表3所示为空载合闸、内部故障和空载投入于内部故障时二次谐波的比值。图6所示为以上三种情况下二次谐波比值的波形。

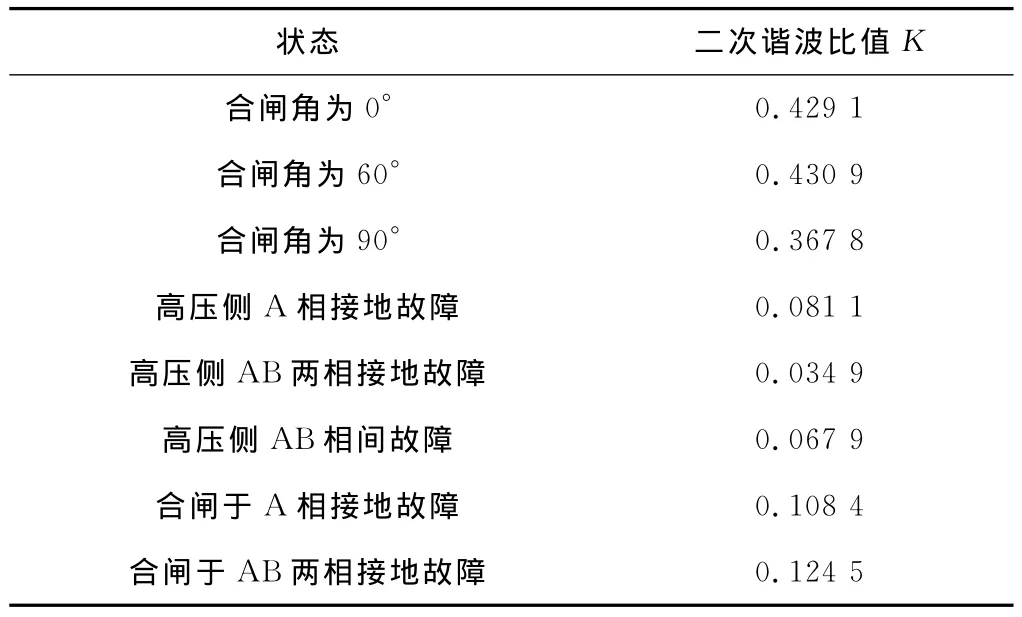
表3 二次谐波最大值与基波最大值的比值

由表3及图6可以看出，空载合闸时对应的二次谐波比值最大，合闸于故障时次之，纯内部故障时最小。因此，可以利用它们之间的明显差异作为闭锁励磁涌流的依据。

4.2 不同故障条件下的差动保护仿真

根据变压器差动保护典型动作判据和逻辑关系，绘制二次谐波制动差动保护动作逻辑，如图7所示。图7中，IA，d、IB，d、IC，d分别为各相差动电流，Iset为不带制动特性的差动继电器整定值，Iset，r为带制动特性的差动继电器整定值，IA2、IB2、IC2分别为各相二次谐波电流有效值，IA1、IB1、IC1分别为各相基波电流有效值。

利用PSCAD搭建的模型可以仿真各种故障情况下变压器差动保护的动作情况。仿真中，故障起始时刻为0.02s，故障持续存在。差动保护中，励磁涌流二次谐波制动比整定值为 K＝0.2[10－12]。

空载合闸时，不同合闸角条件下各保护元件动作响应情况如表4所示，其中，A、B、C分别代表三个相别，数字量“1”代表该元件动作；数字量“0”代表该元件不动作。

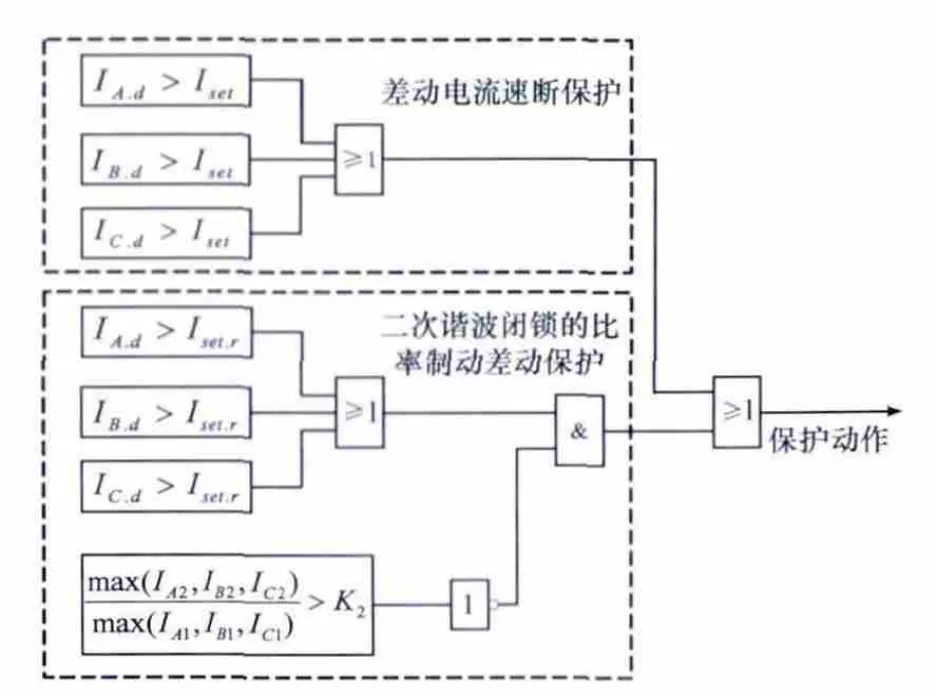
图7 二次谐波制动差动保护逻辑图

空载合闸（剩磁0.3，合闸角0°）、合闸于高压侧A相接地、变压器内部单纯故障（A相接地）3种情况下二次谐波制动差动保护的响应情况如表5所示。

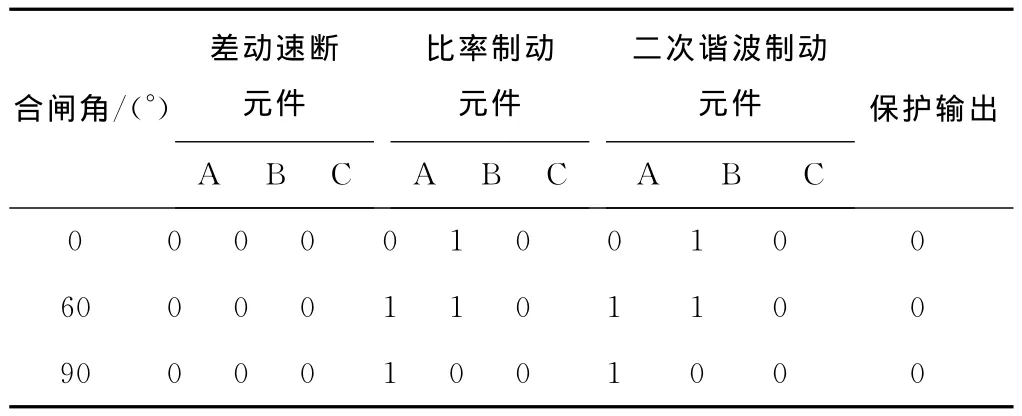
表4 空载合闸时各保护元件动作情况

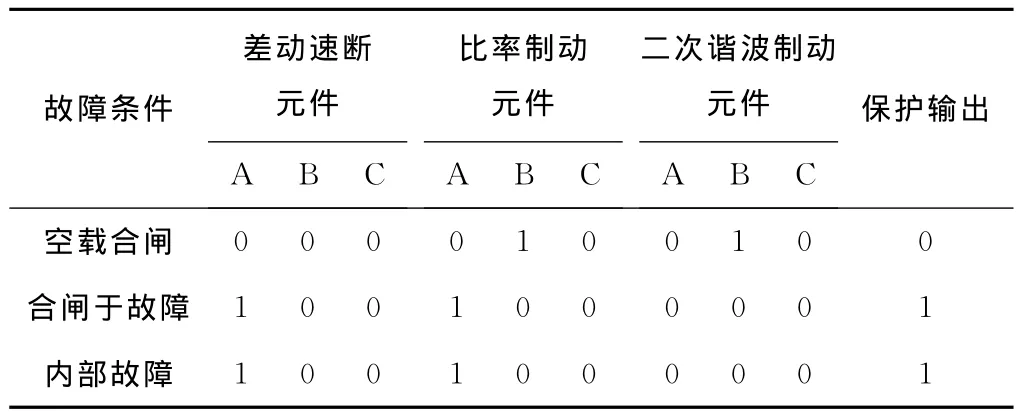
表5 不同故障条件下各保护元件动作情况

对于空载合闸，由于差动速断元件按躲过不平衡电流和最大励磁涌流整定，因此速断保护不应该动作。表4结果显示，在不同合闸角条件下差动速断元件均未出现误动作；空载合闸励磁涌流出现后会导致某相比率制动元件动作，但该相二次谐波制动元件闭锁，保护是可靠的。

对于合闸于区内故障和变压器内部单纯故障，在保护启动后，故障相差动速断元件以及三相比率制动元件都会动作，但二次谐波制动元件不闭锁，保护动作可靠。综上可知，仿真结果与理论分析相一致。

5 结束语

通过Matlab建立的变压器差动保护模型，仿真验证了基于二次谐波制动原理的变压器差动保护方案的正确性。仿真结果表明，数字仿真技术能够形象地反映变压器励磁涌流的产生机制、波形特征及影响因素，完全可以作为变压器差动保护内容的辅助教学或培训工具，使学生更直观地掌握励磁涌流的概念及其对差动保护的影响，进而研究开发出更加可靠的变压器差动保护装置。

（References）

[1]袁宇波，陆于平，李澄，等.三相涌流波形特征分析及差动保护中采用二次谐波相位制动的原理[J].电机工程学报，2006，26（19）：23-28.

[2]陈达壮，张玲.半波傅氏算法与两点乘积算法相结合的励磁涌流识别新方法[J].电力系统保护与控制，2010，38（17）：138-141.

[3]许明，高厚磊，侯梅毅.数字仿真技术在继电保护教学中的应用[J].电力系统保护与控制，2010，38（15）：104-109.

[4]张保会，尹项根.电力系统继电保护[M].北京：中国电力出版社，2009.

[5]王雪，王增平.变压器励磁涌流变权综合识别方法研究[J].电力系统保护与控制，2012，40（6）：63-68.

[6]吕志娟，刘万顺，龚延萍.利用电流波形特征识别变压器励磁涌流和故障电流[J].电力系统自动化，2006，30（19）：53-36.

[7]骆健，吴罡明，丁大德.一种高可靠的自适应励磁涌流制动方法[J].电力系统自动化，2010，34（2）：80-83.

[8]余加霞，张恒泰，葛耀中，等.自适应变压器电流差动保护判据研究[J].电力系统保护与控制，2010，38（18）：115-119.

[9]许正亚.几个励磁涌流新判据分析[J].电力自动化设备，2002，22（1）：23-28.

[10]贺家李，郭征，杨晓军，等.继电保护的可靠性与动态性能仿真[J].电网技术，2004，28（9）：18-22.

[11]刘强，蔡泽祥.基于Matlab的变压器差动保护闭环仿真研究[J].电力自动化设备，2007，27（9）：31-35.

[12]杨奇逊，黄少锋.微型机继电保护基础[M].北京：中国电力出版社，2007.