基于Gabor变换的纹理图像分割算法及应用

朱 峰，王海丰，2，任洪娥*

（1.东北林业大学信息与计算机工程学院，哈尔滨 150040;2.琼州学院电子信息工程学院，海南三亚 572022）

随着计算机技术和数字图像技术的发展，图像处理和计算机视觉也得到了长足的发展，其在很多领域都有广泛的应用。而作为图像基本特征的纹理，是进行图像分析和图像理解的重要因素之一。纹理反映的是图像的灰度统计、空间分布和结构信息，任何图像都可以看作是由一种或多种纹理组成［1］。纹理图像的分析和识别有着非常广泛的应用，并已经渗透到社会生产、生活的各个领域，如卫星遥感图像识别［2－3］、人脸图像识别［4－5］、农林业［6－8］等。而纹理图像分类就是从一个给定纹理类别中识别出给定纹理区域（纹理图像）的纹理图像的类别。通过对图像纹理特征的提取可以对其进行分类、分割等研究。

图像纹理特征的提取方法很多，Gabor滤波器纹理分析方法是一种重要的基于变换的纹理特征提取方法，通过选用某一特定的Gabor函数，设计Gabor滤波器，来实现图像的多尺度、多方向的特征提取。基于Gabor滤波器的纹理分析法是一种空间－频率域联合分析的方法，它克服了传统傅立叶方法的不足，能够最好地兼顾信号在时域和频域中的分辨能力，具有多分辨率特性和良好的方向选择性，能够在空域和频域同时达到最佳分辨率，具有良好的性能。Beck［9］揭示了人类识别纹理图像的能力与二维Gabor滤波器组作用于图像的相关性;DuBuf等［10］利用最小平方逼近的方法研究高阶Gabor滤波器特征，把局部功率谱形状描述为相应的纹理属性;赵银锑等［11］结合人眼特性，利用Gabor滤波器的带通特性，抑制次要纹理图像的主频分量，增强目标纹理的主频分量，将纹理图像分割转化为传统图像分割;黄伟［12］将Gabor滤波器用于提取纹理的特征，通过FCM的聚类来进行普通纹理图像及自然纹理图像分割。为了克服传统Gabor小波低频过表示而高频欠表示的缺点，刘琼等［13］使用极坐标Log Gabor小波进行纹理分析，突破了Gabor小波的带宽限制，仅采用较少的极坐标Log Gabor滤波器和较低的特征向量维数，即实现了准确地纹理分割。文献［6］采用Gabor滤波方法、灰度共生矩阵和几何不变矩提取图像纹理特征等，采用混合的纹理特征，成功实现对木板材表面缺陷的检测。

本文将Gabor小波应用于纹理图像，提取模极值密度作为特征向量，使用聚类算法进行纹理图像的分割，最终将分割算法应用于竹材横端面的识别中。实验结果表明，该方法能有效地对合成纹理图像进行分割，并能成功分离复杂背景下的竹材横端面，取得了非常好的实验效果，为下一步的竹材数控自动化的研究提供了必要的保证。

1 Gabor小波变换及特征提取

1.1 Gabor小波变换

1946年Gabor将窗口傅立叶原子用来测量声音的“频率变化”，将空间依赖性引入到傅立叶分析产生了一种被称为窗口傅立叶变换。

设g（t）=g（－t）是一个实的对称窗口，对它进行平移并做频率调制得gu，ξ=eiξtg（t－u）。

将g规范化为‖g‖=1使得对任意（u，ξ）∈R2有‖gu，ξ‖ =1。f∈L2（R）的窗口 Fourier变换定义为:

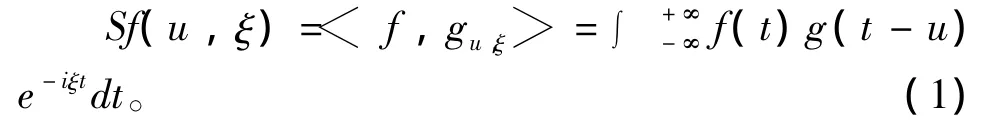
如果这个窗口函数是Gaussian函数时，该变换就变成一个Gabor变换。

将高斯函数进行如下变换就得到高斯基本函数公式 （2）和相应的Fourier变换公式 （3）:

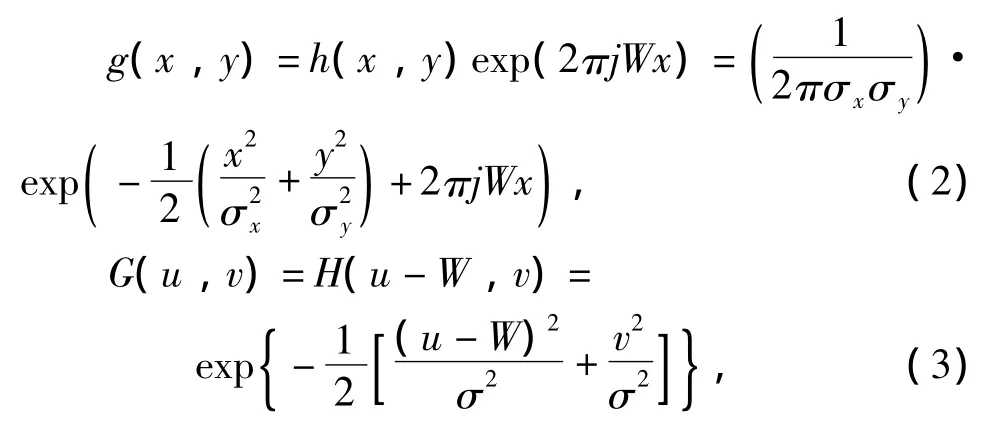
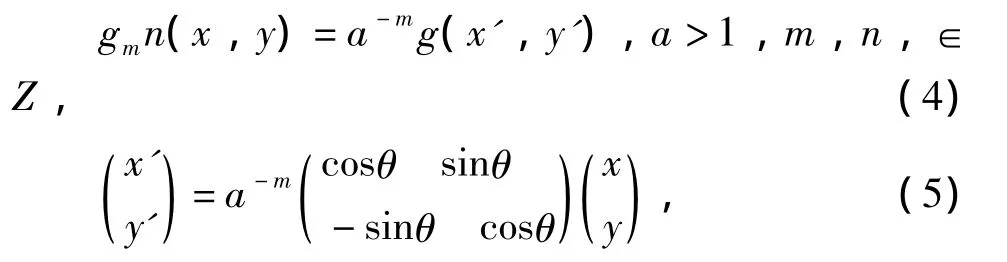
式中:θ=nπ/M，M为总的方向数;g（x，y）为Gabor母小波。

1.2 特征提取

特征提取的方法常常与所研究的纹理密切相关，不同的纹理需要不同的特征，并且特征的好坏直接影响到分类系统的性能。在自然图像中，灰度的不连续性表明物体的轮廓位置，图像中的奇异性和不规则结构中也带有重要的信息。Mallat［14］通过分析信号的奇异性，指出信号的局部奇异性可以由小波变换的模量极大点来描述，并且利用小波模极大值重建原始信号，说明小波模极值在信号处理中有非常重要的作用。基于Gabor变换的模极值特征提取方法如下:

设GT（r，c）为Gabor变换后某子带内的系数，r，c分别为行坐标和列坐标。那么使|GT（r，c）|在r=r0点处达到局部极值，则在r（或c）上取得的极大（小）值分别叫做行（列）模极大（小）值。根据文献［15］的定义:

行模极值密度定义为:

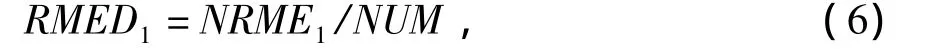
式中:NRME1为子带内行模极值的个数，NUM为子带内系数的个数。

相应地，列模极值密度为:

取各子带的行模极值密度和列极值密度组成特征向量:

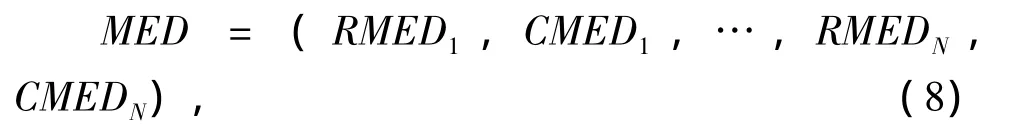
式中:N为除低频子带外的子带数。

为了对信号产生的奇异点进行准确定位，需要对噪声或次要的模极值曲线进行过滤。以降低相同纹理区域的特征变换，并增加不同纹理区域的差别，本文采用的高斯低通滤波器滤波。

式中:h（x，y）为高斯函数;σx和σy分别为g（x，y）沿x轴和y轴的标准方差;W为G（u，v）在u轴上的中心;σx=1/2πσx和 σy=1/2πσy分别为G（u，v）沿u轴和v轴的标准方差。

对高斯基本函数g（x，y）进行尺度变换和旋转变换得到一簇自相似函数，即Gabor小波。其中尺度变换和旋转函数如下。

1.3 基于Gabor变换的纹理图像分割算法

Step 1:对待分割图像F（m，n）进行多尺度、多方向的Gabor变换，得到一系列子带记为GTk l，l=1，2，…，L，k=1，2，…，2n，其中L为最大分解层数，2n为各层分解的方向数目。

Step 2:对得到的各子带采用非线性变换函数进行变换，并通过低通滤波来降低相同纹理区域内特征的变换，增加不同区域的区别。

Step 3:将上述处理得的各子带GTk l对应的像素组成向量，即图像F中点（x，y）的特征向量为并按照公式 （8）进行纹理特征提取，构成原纹理图像对应像素的特征向量。

Step 4:采用分类算法对特征向量进行分类，实现纹理图像的分割。

2 实验及结果分析

为了验证提出的分类算法，选用Bordatz纹理库中的纹理组成两类、四类、五类256×256组合纹理图像进行实验，如图1所示。实验中，滤波器参数设置如下:Ul=0.05，Uh=0.4，S=4，K=6。实验结果如图2所示。

图1 待分割的纹理图像Fig.1 Original Texture Image

图2 纹理图像分割后的结果Fig.2 Segmentation results of the original texture image

为了测试分割效果，定义分割正确率为:

式中:M，N为图像的图像像素数。图1中的三幅合成图像的分割正确率见表1。

表1 正确分割率Tab.1 Successful segmentation rate

从图2（a）可以看出，提出的方法可以很好的对两类纹理进行分割，分割的正确率高达99.25%，仅在纹理相交的边缘地带有少量错误。四类和五类纹理分割错误较多的地方也在纹理图像的边缘地带，对于图像内部具有很好的分割效果。

为进一步验证算法，选取一幅利用相机拍摄的具有复杂背景的竹材横端面图像如图3（a）所示，图中包括竹材横端面和其他背景图像，对其进行分割，具体图像分割结果如图3（b）所示。从图3（b）中可以看出，算法能够实现竹材图像的分割，实验结果令人满意，分割错误较大的部分为人手接触竹材的部分，从图像中可以看出这部分与竹材极为相似。

所有实验结果表明了新算法的有效性，新的纹理提取算法能够很好地完成图像的分类、分割，同样也适用于竹材端面图像，也表明了基于Gabor变换的纹理图像分割算法的潜在应用前景。

图3 竹材横端面及分割结果Fig.3 Original bamboo image and segmentation result

3 结束语

图像分类是计算机视觉领域中一个热点、难点问题，并具有广泛用途。利用Gabor小波变换所具有优良的空间局部性、空间频率及方向选择性，可以捕获图像在不同频率、不同方向下的边缘及局部显著特征，提取图像纹理特征并使用聚类算法实现对纹理图像的分割算法，进而实现对复杂竹材图像的分割。实验结果表明，提出的方法不仅可以有效地提取纹理特征，而且可以有效地实现对图像进行分割、识别，为竹材数控自动化提供了有利的技术支持。

】

［1］任洪娥，王海丰，赵 鹏.新的木材显微细胞图像分类识别方法［J］.计算机工程与应用，2009，45（28）:246 －248.

［2］张 立.基于Gabor函数的遥感影像特征与分类［J］.测绘与空间地理信息，2012，35（4）:123 －124.

［3］陈 波，张友静，陈 亮.结合纹理的SVM遥感影像分类研究［J］.测绘工程，2007，16（5）:23 －27.

［4］杨宏雨，余 磊，王 森.基于Gabor纹理特征的人脸识别方法［J］.计算机应用研究，2011，28（10）:3974 －3976.

［5］白 丽，方 驰，丁晓青.基于皮肤纹理特征的高分辨率人脸图像识别［J］.计算机工程，2012，38（2）:163 －165.

［6］尹建新，祁亨年，冯海林，等.一种基于混合纹理特征的木板材表面缺陷检测方法［J］.浙江农林大学学报，2011，28（6）:937 －942.

［7］曹丽英，张晓贤，伞晓辉.基于图像处理技术和BP神经网络算法的玉米病害诊断方法的研究［J］.计算机科学，2012，39（10）:300－302.

［8］邱 赛，邢艳秋，李立存.基于小波变换的ICESAT－GlAS波形处理［J］.森林工程，2012，28（5）:33 －35.

［9］Beck J，Sutter A，Ivry R.Spatial frequency channels and perceptual grouping in texture segregation［J］.Comput Vis Graph Image Process，1987，37:299 －325.

［10］Du Buf J M H.Abstract Processes in Texture Discrimination［J］.Spatial Vision，1992，6（3）:221 －242.

［11］赵银娣，张良培，李平湘.一种方向Gabor滤波纹理分割算法［J］中国图象图形学报，2006，11（4）:504 －510.

［12］黄 伟.Gabor滤波器的纹理分割［J］.盐城工学院学报（自然科学版），2008，21（3）:9 －13.

［13］刘 琼，周慧灿，王耀南.基于极坐标Log－Gabor小波的纹理分析方法［J］.计算机应用与软件，2008，25（8）:234 －236.

［14］Mallat S.Singularity detection and processing with wavelets［J］.IEEE Trans Information Theory，1992，38（2）:617 －643.

［15］Qiao Y，Sun S.Texture classification using wavelet frame representation based feature［J］.IEEE International Conference on Engineering of Intelligent Systems，2006，2:1775 －1778.