钱塘江嘉绍大桥对强潮河口水动力的影响
谭立心,罗超云,鲁海燕,李最森
(1.广东省长大公路工程有限公司,广东广州 510075;2.浙江省水利河口研究院,浙江杭州 310020)
钱塘江嘉绍大桥对强潮河口水动力的影响
谭立心1,罗超云1,鲁海燕2,李最森2
(1.广东省长大公路工程有限公司,广东广州 510075;2.浙江省水利河口研究院,浙江杭州 310020)
为研究嘉绍大桥对钱塘江涌潮形态及水动力的影响,在分析现场涌潮观测资料的基础上,建立基于KFVS格式的平面二维涌潮数学模型,计算比较了建桥前后涌潮及潮流场的变化。结果表明:受嘉绍大桥阻隔影响,涌潮经过桥位时其形态的整体性被破坏,过桥后约500 m涌潮形态基本恢复,桥位下游涌潮高度增加,桥位上游涌潮高度降低;建桥对涨、落潮流的影响主要在桥位近区,对上下游的潮位和流向影响较小,桥位上下游涨、落潮流速减小0~5%,桥轴线断面桥跨中间流速增加2%~10%;建桥对涌潮的影响是局部的,桥位上下游近区的潮动力有所减弱。
嘉绍大桥;强潮河口;涌潮形态;数值模拟;钱塘江
建桥对水流影响的分析手段主要有实测资料调查分析、数值模拟和物理模型试验等,随着信息技术的提高及数值计算方法的改进,数值模拟因其计算效率高、成本低、不存在模型变率等优点应用日益广泛。张细兵等[1-5]利用二维数学模型模拟了建桥对河流、潮汐和潮流的影响;范平易[6]采用TELEMAC-2D建立二维有限元水动力数学模型,计算了苏通大桥建成后对桥区河段水流和通航条件的影响;傅宗甫等[7]采用三维水动力数学模型分析了异形孔桥墩对水流的影响。上述建桥影响研究大多在潮差不大、潮流动力一般的水动力条件下进行,对于存在强涌潮的河段建桥影响较少涉及。因钱塘江河口存在涌潮等强间断现象,常规的数学模型无法模拟强潮河口地区的浅水间断流动,采用传统的数值格式模拟评价强潮河口建桥的影响存在困难。关于涌潮数值模拟研究,潘存鸿等[8-9]运用以Riemann解为基础的Godunov格式,在四边形网格下建立了钱塘江二维涌潮模型,应用该模型预测了拟建杭州湾萧山通道工程处0.33%、1%、5%潮差频率下的设计流速和设计流量。潘存鸿等[10]应用基于Boltzmann方程的 KFVS(kinetic flux-vector splitting)格式,采用WLTF(water level-bottom topography formulation)方法和特殊的底坡源项处理技术,实现了计算格式的和谐。鲁海燕等[11]在钱塘江涌潮验证的基础上应用该模型,求得0.33%设计潮差频率条件下嘉绍大桥桥位断面设计涨潮流速为7.83 m/s。钱塘江涌潮数值模拟水平的提高为分析强潮河口建桥的影响提供了技术基础。本文采用基于KFVS格式的平面二维涌潮数学模型研究了钱塘江嘉绍大桥对强潮河口水动力的影响,并应用现场涌潮观测资料分析了建桥对涌潮形态的影响。
1 嘉绍大桥及附近水域概况
嘉绍大桥北起嘉兴海宁尖山围垦区,跨钱塘江水域,至上虞九六围垦区,全长10.137 km,共100个桥墩,阻水面积约为5%。大桥的建成一方面加快了钱塘江两岸交通枢纽的发展和完善,另一方面桥墩建设引起的水动力变化可能会影响涌潮景观、河道行洪、船舶航行、河床冲淤以及桥墩自身的安全。因此桥墩对水流的影响是水利、水运、桥梁设计、施工及水行政主管部门共同关心的技术问题。
嘉绍大桥所在的钱塘江尖山河段,受径流和潮流的共同作用,潮差大,其下游澉浦和上游盐官站平均潮差分别为5.68 m和3.27 m,澉浦站实测最大潮差达9.0 m,涌潮强劲,最大潮头高度可达3 m。桥位断面涨潮最大实测垂线平均流速为5.58 m/s,测点最大涨潮流速可达7.5 m/s。大潮期涨急流速在3.74~4.19 m/s之间,落急流速在3.02~4.21m/s之间;中潮期涨急流速在3.19~3.71m/s之间,落急流速在2.78~4.16 m/s之间;小潮期涨急流速在2.03~2.65 m/s之间,落急流速在2.22~3.51 m/s之间。桥位河段泥沙为粉砂,中值粒径在0.02~0.04 mm之间,抗冲能力低,平均沉降速度为0.137 cm/s,起动流速为0.64~0.72 m/s,易冲易淤。
2 平面二维涌潮数学模型的建立与验证
2.1 基本方程
非恒定二维浅水流动方程[10]为

式中:u、v分别为x、y方向的流速分量;h为水深;g为重力加速度;b为河床高程;Sfx、Sfy分别为x、y方向的阻力项。
计算域采用任意三角形剖分,并采用网格中心格式,即将物理量定义在三角形单元形心,控制体即为单元本身。设Ωi为第i个三角形单元域,Γi为其边界,对方程(1)应用有限体积法离散,并利用格林公式得到

式中:Ai为三角形单元 Ωi的面积;(cos θ,sin θ)为 Γ外法向单位向量;dl为线积分微元。对式(2)时间导数采用前差,并记Fm=Fcos θ+Gsin θ,得到基本数值解公式为

式中:Δt为时间步长;lj为三角形边长;S0i为底坡源项;Sfi为阻力项;上标n为时间步数;下标j表示i单元第j边。
求解式(3)的核心是计算法向数值通量。本文采用KFVS格式[9]求解法向数值通量,该格式具有计算稳定、模拟精度高、守恒性好等优点。但当计算域存在动边界时,往往不能直接应用上述方法求解界面法向数值通量,采用能模拟间断流的干底Riemann解求解干、湿单元界面的数值通量[12]。
2.2 计算域及桥墩的概化
计算域下边界取在澉浦—西三连线,上边界为钱塘江的富阳和曹娥江的三江闸断面,计算域面积约为656 km2,如图1所示。计算域内的网格布设考虑了水流和地形变化的差异,对大桥附近区域的计算网格适当加密,以便更好地反映这些区域的水流和地形变化特征,保证流场模拟精度。整个计算域内共布设81324个三角形单元和41374个有效节点,最小空间步长为3m,水流计算的时间步长为0.1s。
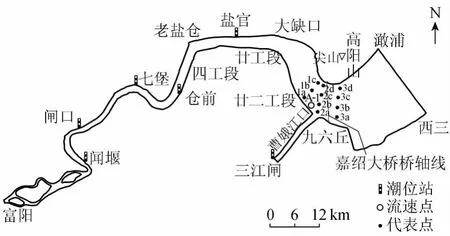
图1 嘉绍大桥数学模型计算范围及测点位置
数学模型计算中桥墩的概化方法有多种,现有处理方法主要有加密网格法、附加糙率法、阻水面积置换法和附加阻力法等。本文采用加密网格法和附加糙率法来考虑建桥对水流的影响:通过局部加密桥墩处网格将桥墩的边界作为封闭边界来处理,采用这种方法处理的桥墩,其所在网格不过水;考虑到平面二维数学模型无法模拟桥墩处的上升流及涡旋等,根据经验公式[13]将桥墩上下游各30 m范围的网格进行加糙处理,加糙后的涨、落潮糙率为建桥前的10倍左右。
2.3 糙率的给定
按照上游糙率大于下游糙率,落潮糙率大于涨潮糙率,涌潮河段涨、落潮糙率小于上下游河段涨、落潮糙率的原则给定各河段的涨、落潮糙率,并根据实测水文资料来调试各河段的糙率值,嘉绍大桥附近河段涨、落潮糙率分别为0.005和0.0065。
2.4 初始和边界条件
初始水位采用沿程实测水位站的初始潮位进行内插,x方向和y方向初始流速为零。数学模型计算的下游水边界条件由澉浦站实测潮位过程给定,上游水边界为水文测验期间富春江电站日平均下泄流量。由壁面的不穿透性,取陆域边界法向流速为零。
2.5 模型的验证
利用2005年6月和2007年10月实测水文资料对模型进行验证。验证的地形资料采用与水文测验期间对应或基本接近的水下地形图。模型验证了闻堰、闸口、七堡、仓前、盐官、廿工段、廿二工段、曹娥江口的潮位过程及桥位断面的流速过程,限于篇幅,文中仅列出嘉绍大桥南岸测站的水位及流速过程验证图。图2为2007年10月曹娥江口站的潮位过程验证图,图3为桥位南岸测点A-1的流速、流向过程验证图。由图2、图3可见,曹娥江口潮位的涨、落潮过程及高、低潮位计算值与实测值吻合较好,测点A-1的流速、流向过程及位相计算值与实测基本吻合,且涨潮过程呈直角三角形分布,桥位处由落潮流快速转为涨潮流,流速瞬间变幅达3 m/s,模型较好地模拟了流速的突变,说明本文建立的数学模型可用于桥梁建设前后涌潮河段的流场计算分析。

图2 2007年10月曹娥江口潮位过程验证

图3 2007年10月嘉绍大桥桥位南岸测点A-1流速、流向过程验证
3 模型计算结果及分析
3.1 建桥对涌潮的影响
2009年9月大潮期间嘉绍大桥现场涌潮观测表明,涌潮在向上游传播的过程中,受两岸地形的约束和水深的影响,南、北岸涌潮形态呈线性分布,北岸涌潮较南岸传播更快,故先到达大桥附近,涌潮从东北向西南方向传播,与大桥主通航孔轴线夹角约为45°,受嘉绍大桥阻隔影响,涌潮经过桥位时其形态的整体性被破坏,桥轴线下游涌潮高度增加,涌潮传播通过大桥后至上游约500 m,其形态基本恢复,桥轴线上游涌潮高度有所降低。图4为嘉绍大桥现场观测到的涌潮。

图4 涌潮通过大桥时的照片
根据本文数学模型计算的建桥前后的流场、涌潮传播方向与现场观测情况一致,建桥后大范围的流矢变化不大,仅在桥轴线附近朝逆时针方向略微偏转,建桥对涌潮的产生及传播基本无影响。
图5为建桥前后桥位上下游涌潮时的潮位变化过程线,图5表明,建桥前桥位上游1 min涌潮高度为0.40 m,建桥后为0.36 m,降低了0.04 m;建桥前桥位下游1 min涌潮高度约为0.72 m,建桥后约为0.75 m,抬高了0.03 m。可见建桥将降低桥位上游涌潮高度,而略抬升桥位下游涌潮高度,总体而言,涌潮高度变化幅度不大。
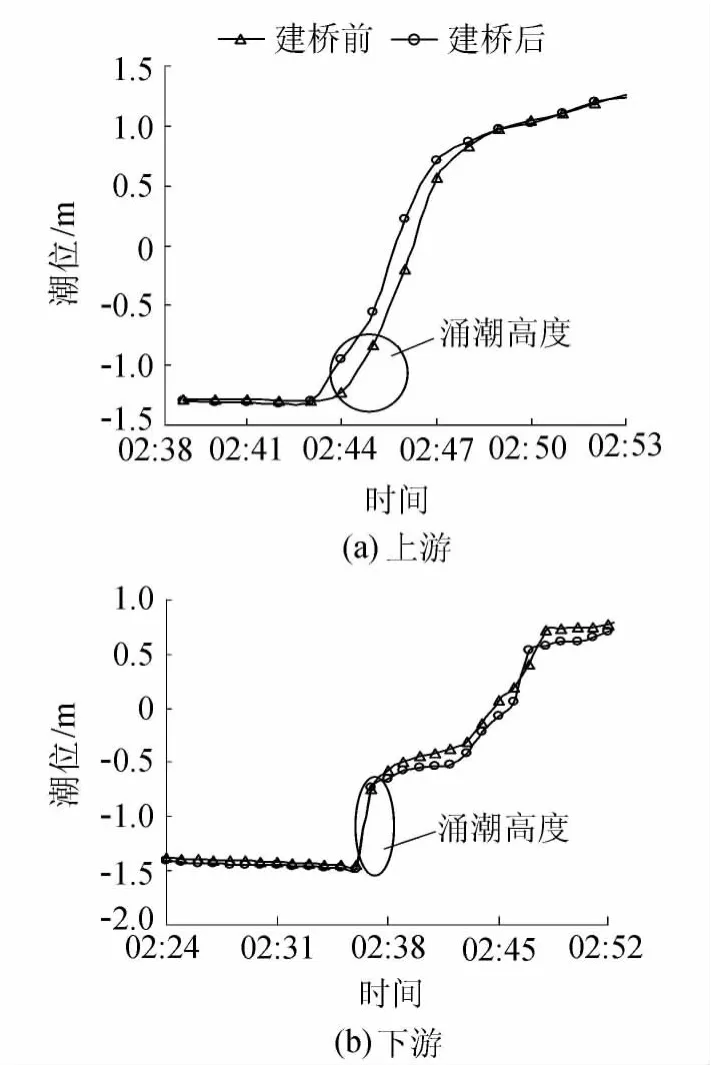
图5 2007年10月8日建桥前后桥位上下游涌潮潮位的变化过程线
3.2 建桥对潮流的影响
应用经验证后的数学模型,计算分析了澉浦潮差频率为10%和0.33%条件下建桥对钱塘江河口潮流的影响,计算采用的地形与验证地形一致,上边界为富春江电站多年平均流量1000 m3/s,曹娥江口水边界按曹娥江大闸建成后考虑,下边界分别给定澉浦潮差频率为10%和0.33%时的潮位过程。
为分析建桥对桥位上下游潮流的影响,统计建桥前后澉浦、桥南岸下游、桥南岸上游、曹娥江口、大缺口等5处的高、低潮位变化,并选取桥轴线上游的廿二工段、曹娥江口和桥轴线下游的九六丘断面的11个代表点(位置见图1)的涨、落潮流速变化进行建桥影响分析。表1为建桥后桥位上下游水位的变化,表2列出了10%潮差频率条件下代表点流速的变化,0.33%潮差频率条件下各代表点流速变化情况与之类似,在此不一一列出。建桥后主墩对附近水域的影响较其他桥墩大,故主墩处流速、流向变化有一定的代表性,图6为桥位南侧主墩附近涨急时刻流矢,图7为桥位南侧主墩附近涨潮平均流速变化等值线。
分析图6、图7、表1、表2中的数据,将建桥对钱塘江水域潮流的影响归纳如下:①建桥后对潮位的影响表现为涨潮时桥下游因桥墩壅水致高潮位有所抬高,影响范围至澉浦附近,以10%潮差频率大潮为例,桥下游高潮位抬高1~3 cm;桥上游则因进潮量减少使高潮位有所降低,影响范围至大缺口,桥位上游高潮位降低约2 cm。落潮时则相反,桥位上游低潮位抬高,下游降低,影响幅度大致与高潮位相当。②建桥对流向的影响较小,流向改变处主要位于桥墩上下游侧,在桥墩附近形成类似绕流现象,过桥墩后大约200 m流向基本恢复。③建桥后,桥位近区除主通航孔上下游一定范围流速有所增加外,其余范围流速减小,影响范围为桥位上游8 km至桥位下游3km。对于桥轴线断面,桥墩之间流速增大,南、北两侧边跨桥孔流速增大的幅度较其余地方略大约10%,南侧主通航孔流速增加约6%,北侧主通航孔流速增加约4%,其余桥跨增加2% ~4%。桥墩上下游侧近区因受桥墩的作用,涨、落潮流速减小2% ~6%。桥位上游靠南岸一侧,曹娥江口以西至绍兴岸段涨潮流速增加0~2%,落潮流速减小0~2%,曹娥江大闸附近涨、落潮流速减小约2%;靠北岸一侧(1c和2d代表点),涨、落潮流速减小2% ~4%。桥位下游(九六丘断面代表点)涨、落潮流速减小0~2%。
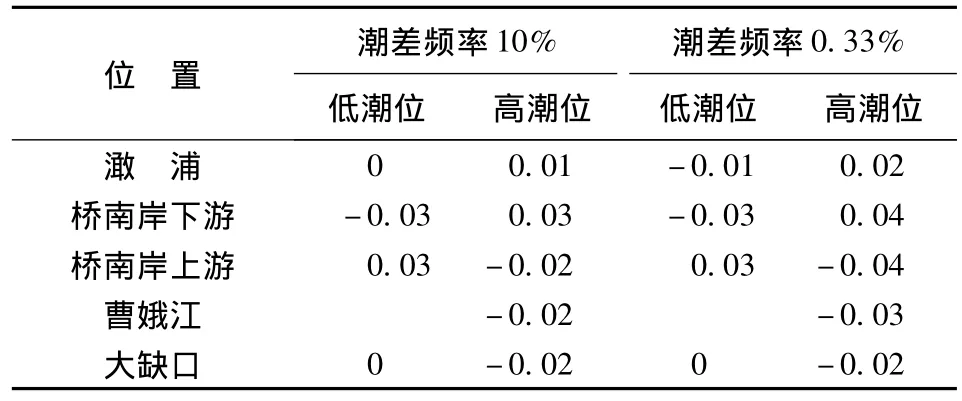
表1 建桥后不同潮差频率下潮位的变化 m
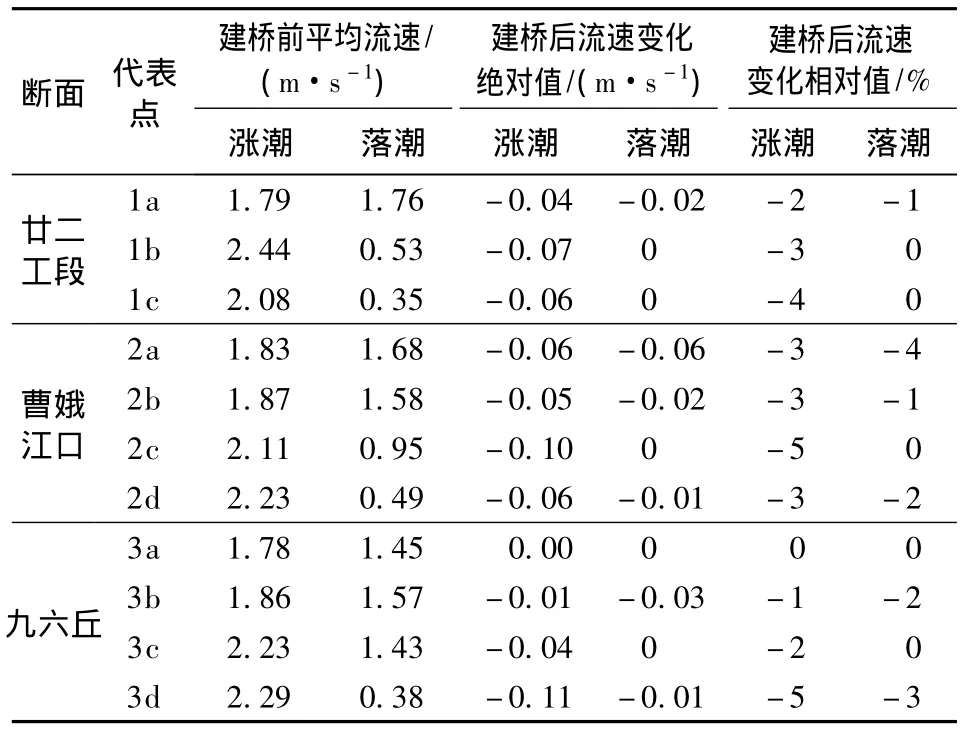
表2 建桥前后各代表点流速变化(10%潮差频率)
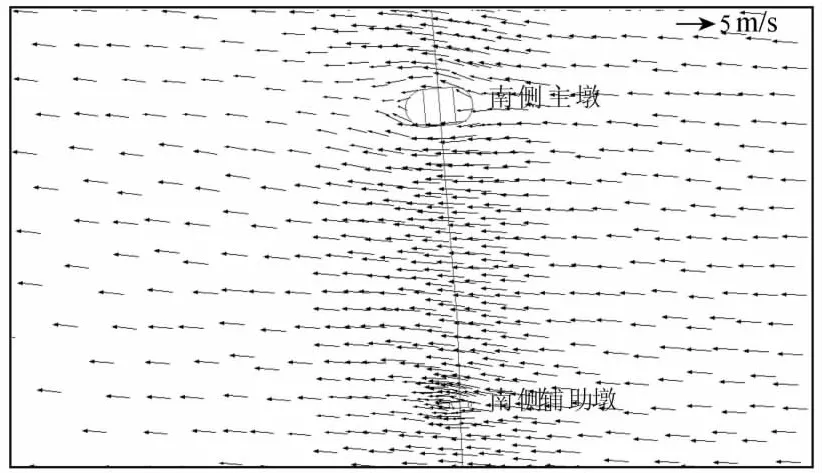
图6 桥位南侧主墩附近涨急时刻流矢
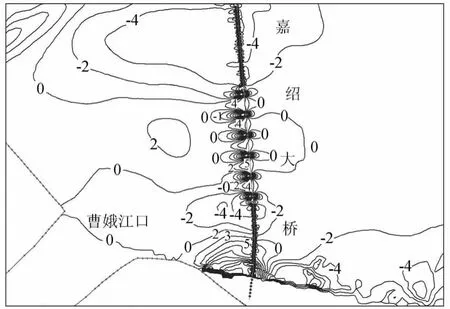
图7 桥位南侧主墩附近涨潮平均流速变化等值线(单位:%)
4 结语
本文建立了基于KFVS格式的有限体积法二维涌潮数学模型,并应用实测资料对模型参数进行验证,结果表明该模型能用于钱塘江河口桥梁工程的影响研究。应用该模型计算分析了嘉绍大桥建成后对钱塘江水动力的影响,同时应用现场观测资料分析了建桥对涌潮形态的影响。结果表明:澉浦潮差10%、0.33%频率条件下,嘉绍大桥建成后桥位上游高潮位降低,低潮位抬高,桥位下游高潮位抬高,低潮位降低,变化幅度在5 cm以内;大桥建成对潮流的影响主要集中在桥位近区,对流向的影响较小,桥轴线断面各桥跨间涨、落潮流速增加2% ~10%,桥位上下游涨潮和落潮流速减小0~5%;嘉绍大桥建成后对桥区涌潮形态的整体性产生一定的扰动影响,桥位下游涌潮高度增加,过桥后约500 m涌潮形态基本恢复,桥位上游涌潮高度有所降低,对涌潮的产生和传播不产生影响。
[1]张细兵,余新明,金琨.桥渡壅水对河道水位流场影响二维数值模拟[J].人民长江,2003,34(4):23-24.(ZHANG Xibing,YU Xinming,JIN Kun.Numerical simulation of flow field inupstream back water area of bridge and aqueduct[J].Yangtze River,2003,34(4):23-24.(in Chinese))
[2]曹民雄,甘小荣,周丰年,等.潮汐河段桥墩对水流影响的数值计算与分析[J].人民长江,2006,37(4):81-84.(CAO Mingxiong,GAN Xiaorong,ZHOU Fengnian,et al.Numerical computation and analysis of flow influenced by bridge piers in a tidal reach[J].Yangtze River,2006,37(4):81-84.(in Chinese))
[3]朱军政,曹颖.潮汐河口多座桥梁行洪影响的分析[J].水动力学研究与进展:A辑,2006,21(5):592-598.(ZHU Junzheng,CAO Ying.Effects of multi-bridge piers on flooding at tidal estuary[J].Chinese Journal of Hydrodynamics,2006,21(5):592-598.(in Chinese))
[4]崔玉炎,杨芳.二维水流数学模型在河道桥梁阻水计算中的应用[J].中国农村水利水电,2007(7):97-101.(CUI Yuyan,YANG Fang.Application of 2D mathematical model to resistance computation in bridge project[J].China Rural Water and Hydropower,2007(7):97-101.(in Chinese))
[5]李文丹,李孟国,杨树森,等.港珠澳大桥建设对水沙环境影响数学模型研究:模型的建立和验证[J].水运工程,2011(8):3-8.(LI Wendan,LI Mengguo,YANG Shusen,et al.Mathematical modeling of the effect of constructing Hongkong-Zhuhai-Macao bridge on hydrodynamic sedimentenvironmentdevelopmentand verification ofthe model[J].Port& Waterway Engineering,2011(8):3-8.(in Chinese))
[6]范平易.桥区流场数值模拟及建桥对通航的影响研究[D].上海:上海交通大学,2010.
[7]傅宗甫,赵春潮,安建峰.异形孔桥墩附近河道水流流动特性[J].河海大学学报:自然科学版,2011,39(4):402-406.(FU Zongfu,ZHAO Chunchao,AN Jianfeng.Flow characteristics around bridge pier with special orifice[J].Journal of Hohai University:Natural Sciences,2011,39(4):402-406.(in Chinese))
[8]潘存鸿,林炳尧,毛献忠.求解二维浅水流动方程的Godunov格式[J].水动力学研究与进展:A 辑,2003,18(1):16-23.(PAN Cunhong,LIN Bingyao,MAO Xianzhong.A Godunov-type scheme for 2-D shallow-water flow with bottom topography[J].Chinese Journal of Hydrodynamics,2003,18(1):16-23.(in Chinese))
[9]潘存鸿,鲁海燕,陈甫源,等.涌潮数学模型在钱塘江河口桥梁工程中的应用[J].浙江水利科技,2004(5):1-4.(PAN Cunhong,LU Haiyan,CHEN Fuyuan,et al.Application of numerical model of tidal bore to bridge works in the Qiantang Estuary[J].Zhejiang Hydrotechnics,2004(5):1-4.(in Chinese))
[10]潘存鸿,徐昆.三角形网格下求解二维浅水方程的KFVS 格式[J].水利学报,2006,37(7):858-864.(PAN Cunhong,XU Kun.Kinetic flux vector splitting scheme for solving 2-D shallow water equations with triangular mesh[J].Journal of Hydraulic Engineering,2006,37(7):858-864.(in Chinese))
[11]鲁海燕,潘存鸿,卢祥兴.钱塘江嘉绍大桥设计涨潮流速计算[J].浙江水利科技,2008(5):1-4.(LU Haiyan,PAN Cunhong,LU Xiangxing.Computation of design velocity of Jiashao Bridge in the Qiantang River[J].ZhejiangHydrotechnics,2008(5):1-4.(in Chinese))
[12]潘存鸿,林炳尧,毛献忠.浅水问题动边界数值模拟[J].水 利 水 运 工 程 学 报,2004(4):1-7.(PAN Cunhong,LIN Bingyao,MAO Xianzhong.Numerical simulation of moving boundary for solving shallow water equations[J].Hydro-Science and Engineering,2004(4):1-7.(in Chinese)
[13]罗肇森.孙梅秀.河工模型中几种人工糙率的计算[J].水利水运科学研究,1981(2):71-81.(LUO Zhaosen,SUN Meixiu.Calculation of several types of artificial roughness elements in river models[J].Hydro-Science and Engineering,1981(2):71-81.(in Chinese))
Impacts of Jiashao Bridge on the hydrodynamics field in the Qiantang Estuary
TAN Lixin1,LUO Chaoyun1,LU Haiyan2,LI Zuisen2(1.Guangdong Provincial ChangDa Highway Engineering Co.,Ltd.,Guangzhou510075,China;2.Zhejiang Institute of Hydraulics and Estuary,Hangzhou310020,China)
According to the observed data of the tidal bore shape,a 2-D mathematical model based on the KFVS(kinetic flux-vector splitting)scheme was employed to study the impact of Jiashao Bridge on the current field of the Qiantang River.The results show that the integral morphologic of the tidal bore is destroyed due to the bridge piers,when the bore passing,the tidal bore shape recovers about 500 m upstream of the bridge site.The bore height downstream of the bridge site rises,and that of upstream of the bridge site lowers.The maximum impact of the bridge construction occurs at the adjacent area of the bridge axis,and little impact on the variation of the tidal level,and the tidal volume of upstream and downstream reach.The flood and ebb flow velocity of upstream and downstream reach decreased about 0-5%,and that between bridge piers at the bridge axis cross-section increased amount 2% -10%.The impact of Jiashao Bridge on the tidal bore is local;hydrodynamics power at upstream and downstream of bridge site will be weakened.
Jiashao Bridge;macro-tidal estuary;tidal bore shape;numerical simulation;Qiantang River
TV131.2
A
1006-7647(2013)06-0061-05
10.3880/j.issn.1006-7647.2013.06.013
国家自然科学基金(51109188);浙江省自然科学基金(LY12E09010);浙江省创新团队建设与人才培养项目(2011F20019)
谭立心(1975—),男,湖南长沙人,高级工程师,博士研究生,主要从事桥梁工程研究。E-mail:tanlixin@vip.163.com
鲁海燕(1976—),女,湖北天门人,高级工程师,硕士,主要从事河口海岸工程研究。E-mail:luhy8902@sina.com
2012-12-06 编辑:骆 超)

