基于copula回归模型的损失预测

孟生旺，刘新红，2

（1．中国人民大学 应用统计科学研究中心，北京 100872；2．北京石油化工学院 数理系，北京 102617）

一、引 言

在非寿险损失预测中，经常假设损失次数与损失强度相互独立，并分别建立损失次数和损失强度的广义线性模型。广义线性模型中常用的分布假设是指数分布族中的分布，包括二项分布、泊松分布、伽马分布和逆高斯分布。在损失次数的广义线性模型中，泊松分布最为常用［1］81－88。当损失次数数据存在零膨胀或过离散时，需要将泊松分布扩展到零膨胀泊松或过离散泊松［2］，而解决过离散和零膨胀损失次数数据的另一种方法，是建立负二项回归模型或零膨胀负二项回归模型［3］；在损失强度的广义线性模型中，伽马分布最为常见，但当损失强度数据存在尖峰厚尾特征时，逆高斯分布假设下的广义线性模型对实际数据的拟合效果更好［4］。

在损失次数与损失强度相互独立的假设下，可将损失次数与损失强度的预测值相乘而求得总损失的预测值，这种方法简单易行，在非寿险精算实务中应用广泛，其缺陷是忽略了损失次数与损失强度之间的相依关系，可能造成总损失的预测偏差［5］。

copula在刻画随机变量的相依性方面具有独特优势，不受边缘分布的影响。对于二元连续分布函数而言，对应着唯一的copula函数，因此可以应用coplua函数建立两个连续型随机变量之间的相依关系，譬如可以利用copula研究损失强度在不同时期的相依问题和不同险种在损失强度上的相依问题以及不同险种在赔款准备金上的相依问题［6－9］。但当边缘分布为离散分布时，copula函数的唯一性将无法得到保证，这就增加了应用copula刻画两个随机变量之间相依关系的难度。

二、copula回归模型

（一）损失次数的广义线性模型

在非寿险损失预测中，通常假设损失次数服从泊松分布、过离散泊松分布、负二项分布或各种对应的零膨胀分布，这些分布在零点都有较大的概率取值，表示损失不会发生。分布的均值表示期望的损失次数，当损失次数为零时，损失强度必然为零。为了便于应用copula函数建立损失次数与损失强度之间的相依关系，假设损失已经发生，并在此条件下建立总损失的预测模型。在损失已经发生的前提下，损失次数的分布在零点没有概率，可以用零截断分布进行描述，而相应的损失强度也必然大于零，可以用伽马分布或逆高斯分布进行描述。

在损失已经发生的条件下，假设损失次数服从零截断泊松（zero－truncated Poisson，ZTP）分布，概率函数可以表示为：

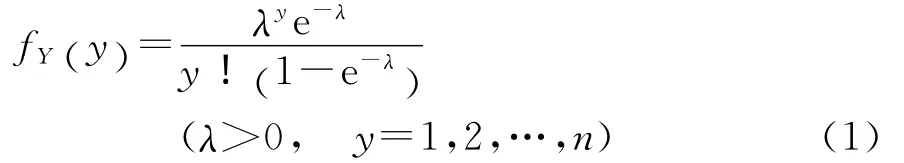
将零截断泊松分布的参数表示为解释变量的函数，即得损失次数的广义线性模型为：

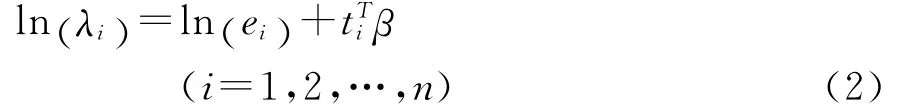
其中ei是风险单位数，ti∈Rp为解释变量组成的向量，β是p维的系数向量。

（二）损失强度的广义线性模型

损失强度的分布可以采用伽玛分布或逆高斯分布，伽玛分布的概率密度函数为：

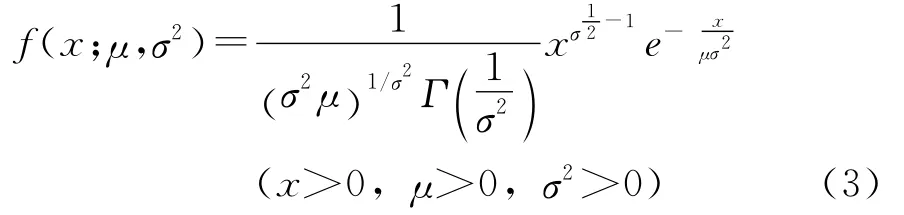
其均值、方差、偏度和峰度分别为：μ，σ2μ2，2σ，6σ2。逆高斯分布的概率密度函数为：

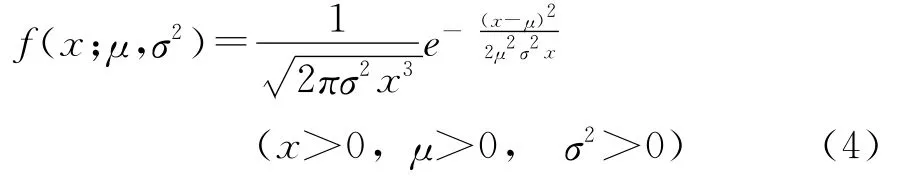
其均值、方差、偏度和 峰度分 别为：μ，σ2μ3，3σ，15μσ2。逆高斯分布的概率密度函数相对于伽玛分布形式更加灵活，可以描述从对称到尖峰厚尾的各种分布形态。

在前述的伽马分布或逆高斯分布中，把均值表示为解释变量的函数，可得到损失强度的广义线性模型，即：

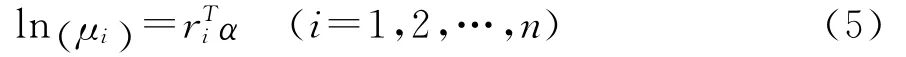
其中ri∈Rq为解释变量组成的向量，α是q维的系数向量。

（三）常用的copula函数

copula函数为相依风险的分析提供了一个有力工具。根据Sklar定理［12］17－23，若F和G是随机变量X、Y的边缘分布函数，H是随机向量（X，Y）的联合分布函数，那么存在一个copula函数C满足：反之，如果C是一个copula函数，F和G分别是随机变量X和Y的分布函数，则联合分布函数H可以通过式（6）得到；如果F和G都是连续的，则C是唯一确定的。

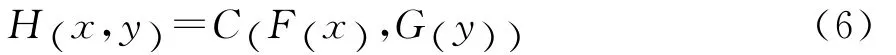
比较常用copula函数的分布函数如下：

1．Gauss Copula函数：

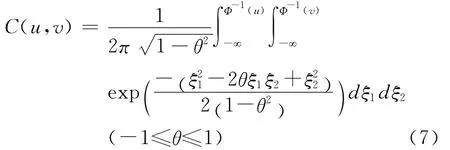
其中Φ（·）为标准正态分布的分布函数。Gauss Copula的密度函数是对称的，Kendall’sτ秩相关系数为arcsinθ。2．Clayton Copula函数：

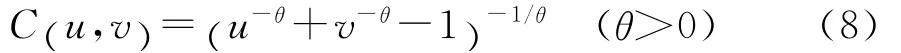
当参数θ→0时，表示两个随机变量相互独立；当θ→＋!时，两个随机变量完全相关。Clayton Copula密度函数具有非对称性，上尾低下尾高，对下尾处的变化比较敏感，下尾相关系数为λL＝2－1／θ，Kendall’sτ秩相关系数为θ／（θ＋2）。

3．Gumbel Copula函数：

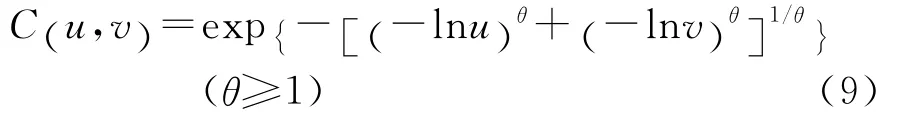
当参数θ＝1时，表示两个随机变量相互独立；当θ→＋!时，两个随机变量完全相关。Gumbel Copula密度函数也具有非对称性，上尾高下尾低，对上尾处的变化比较敏感，上尾相关系数为λU＝2－21／θ，Kendall’sτ秩相关系数为1－1／θ。

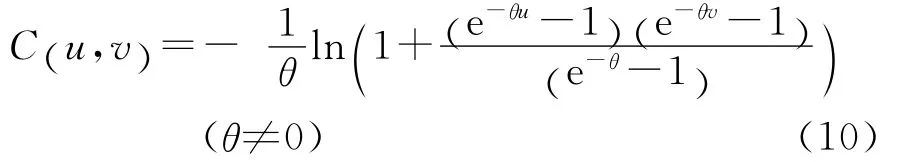
4．Frank Copula函数：

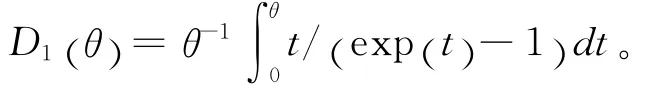
（四）损失次数与损失强度的copula回归模型

损失次数Y与损失强度X的相依关系可通过copula函数刻画，而相依性的大小可通过尾部相关系数和Kendall’sτ秩相关系数衡量。损失次数与损失强度的联合概率密度函数可表示为［11］：中

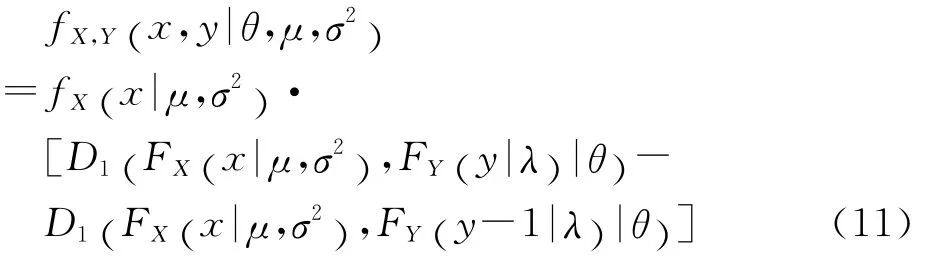
联合式（2）～（4），即可在不同的copula函数和不同的分布假设下得到相应的copula回归模型。譬如把式（1）和式（3）代入式（11），并应用式（8）中的Clayton copula函数，即可得到在零截断泊松分布和伽马分布假设下的Clayton copula回归模型的似然函数，并应用极大似然法求得未知参数α、β、σ2、θ的估计值。Copula回归模型的参数估计值没有显式解，需要应用数值算法求解。

三、Copula回归模型在损失预测中的应用

下面应用前述的copula回归模型，拟合一组车险保单的损失数据。该数据包括67 856份车险保单的损失记录，其中有4 624份保单在保险期间至少发生过1次损失，解释变量包括汽车用途、汽车年龄、驾驶员性别、驾驶员年龄和行驶区域［1］。

不考虑解释变量的情况下，损失次数与损失强度的Pearson线性相关系数为0．076，Kendall’sτ秩相关系数为0．152，Spearmanρ秩相关系数为0．184，且在统计上都显著不为零，说明损失次数与损失强度之间存在显著的相依关系。

原始数据中，共有4 624份保单发生过损失。对于这些保单，在建立copula回归模型时，假设每份保单的损失次数服从零截断泊松分布（ZTP），损失强度服从伽马分布（GA）或逆高斯分布（IG），用前述的四种copula函数描述损失次数与损失强度之间的相依关系。

（一）损失强度服从伽玛分布的copula回归模型

经检验，在损失次数服从零截断泊松分布（ZTP）的广义线性模型中，所有解释变量都不显著，损失次数模型只包含截距项。在损失强度服从伽玛分布（GA）的广义线性模型中，显著的解释变量包括驾驶员的年龄、性别和汽车车龄。相应的copula回归模型如下：

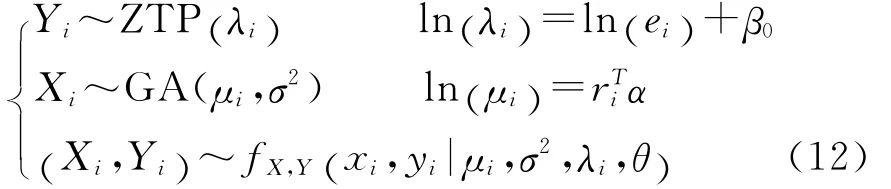
应用R中的copreg程序包可求得模型参数的估计值，见表1、2、5。表1中β0是损失次数模型中的常数项，θ是copula中的参数，τ是kendall’sτ秩相关系数，σ2是伽马分布中的离散参数。不同copula函数下的对数似然函数值如表1的最后一列所示。）

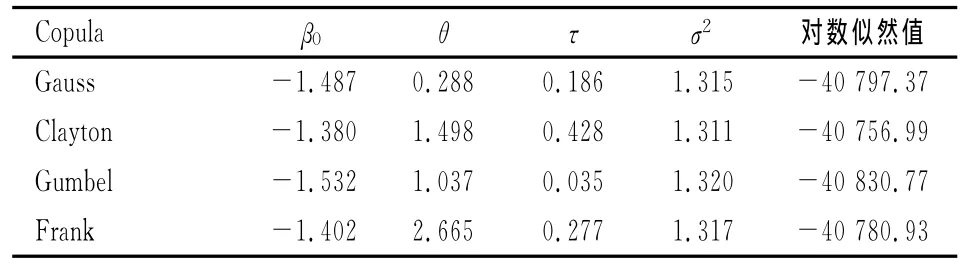
表1 伽马分布假设下copula回归模型参数估计值表

为了对不同copula函数下的回归模型进行比较，可以使用Vuong检验［11］，检验统计量为：

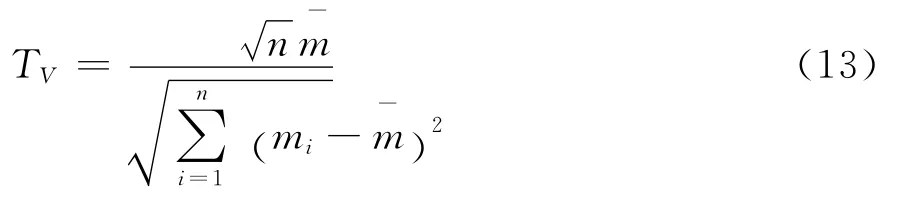
表2 伽马分布假设下copula回归模型逐对Vuong检验表

（二）损失强度服从逆高斯分布的copula回归模型

当损失强度呈现尖峰厚尾特征时，逆高斯分布的拟合效果会优于伽马分布。如果假设损失次数仍然服从零截断泊松分布（ZTP），但损失强度服从逆高斯分布（IG），相应的copula回归模型则为：

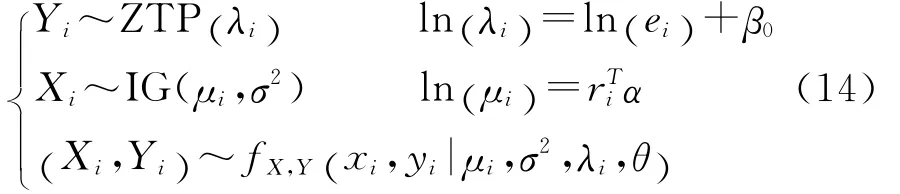
上述模型的参数可以通过极大似然法进行估计，结果如表3、4、5所示。比较表1表3可见：在各种copula回归模型中，逆高斯分布假设下的对数似然值都大于伽马分布假设下的对数似然值；在各种copula回归模型中，表2表4的Vuong检验都表明Clayton copula回归模型优于其他copula回归模型；表6的AIC值表明：逆高斯分布假设下的copula回归模型普遍优于伽马分布假设下的copula回归模型，而且逆高斯分布假设下Clayton copula回归模型的AIC最小。由此可见，对于本文的数据而言，损失次数服从零截断泊松分布，而损失强度服从逆高斯分布的Clayton copula回归模型是相对最优的模型。在该模型中，下尾相关系数为0．647，Kendall’sτ秩相关系数为0．443，表明损失次数与损失强度存在明显的正向相依关系。

在该模型中，每个车年的期望损失次数未受保单风险特征的影响，所有保单的期望损失频率估计值均为exp（－1．467）＝0．231，但不同保单每次损失对应的期望损失强度与保单的风险特征（解释变量）有关。譬如对于驾驶员年龄为水平1、性别为女、车龄为水平1的保单，平均每次损失对应的损失强度为exp（7．710）＝223。该模型的参数估计结果表明：随着驾驶员年龄的增大，损失强度会减少，譬如当驾驶员年龄为水平2时，损失强度降低为基准水平（驾驶员年龄为水平1）的exp（－0．217）＝80．48%；男性驾驶员比女性驾驶员的损失强度增加了exp（0．167）－1＝18．13%；随着汽车车龄的增加，损失强度也会增加，譬如车龄2的损失强度是基准水平（车龄1）的exp（0．052）＝105．35%，但在统计上不显著，即与车龄1的损失强度没有显著的统计差异。当损失强度服从伽玛分布和损失次数服从零截断泊松分布时，总损失的分布是无限混合的伽玛分布［11］。单个伽玛分布有一个众数，是右偏分布，混合后总损失的概率分布会更偏，而且有多个众数。当损失强度服从逆高斯分布时，总损失的概率分布将比伽马分布假设下更偏、尾部更厚。表6是分别应用独立假设下的广义线性模型、损失强度服从伽玛分布的copula回归模型以及损失强度服从逆高斯分布的copula回归模型，对总损失的拟合结果。如果假设损失次数与损失强度相互独立，无论使用伽马分布还是逆高斯分布，广义线性模型对总损失的拟合值都是偏低的（实际总损失为10 284 179）。

表3 逆高斯分布假设下copula回归模型参数估计值表

表4 逆高斯分布假设下copula回归模型的逐对Vuong检验表

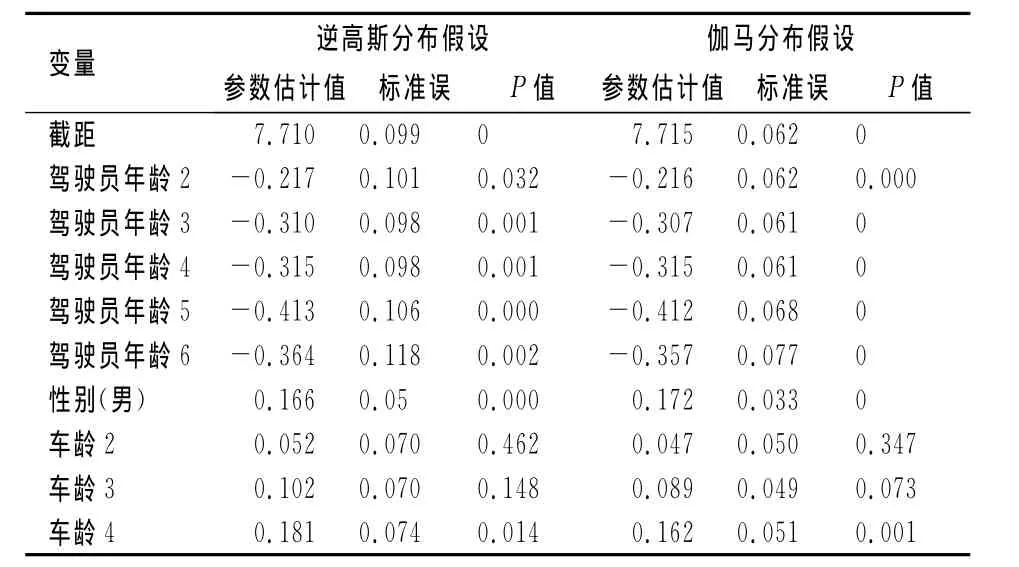
表5 Clayton copula回归模型中损失强度的系数估计值表

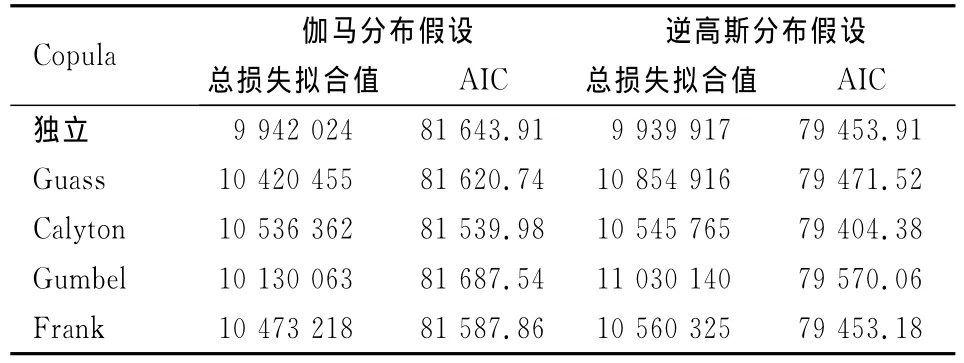
表6 模型比较表

四、结 论

在非寿险损失预测中，通常假设损失次数与损失强度相互独立。本文基于一组实际数据的实证研究结果表明：这种假设可能与实际不符，从而导致对损失的低估；损失次数与损失强度的相依性，可以通过copula函数进行描述；在常用的copula函数中，既有上尾相依的Gumble Copula，也有下尾相依的Clayton Copula，还 有 对 称 的 Gauss Copula 和Frank Copula。把损失次数和损失强度的广义线性模型与描述它们相依性的copula函数相结合建立的copula回归模型可以有效改进对实际损失的拟合效果；在损失已经发生的条件下，假设损失次数服从零截断泊松分布，损失强度服从逆高斯分布的Cayton copula回归模型对本文研究的一组实际数据，具有相对更好的拟合效果。

［1］ Jong P d，Heller G Z．Generalized Linear Models for Insurance Data［M］．Cambridge：Cambridge University Press，2008．

［2］ 孟生旺，徐昕．非寿险费率厘定的索赔频率预测模型及其应用［J］．统计与信息论坛，2012（9）．

［3］ 徐昕，袁卫，孟生旺．零膨胀负二项回归模型的推广与费率厘定［J］．系统工程理论与实践，2012（1）．

［4］ 孟生旺．广义线性模型在汽车保险定价的应用［J］．数理统计与管理，2007（1）．

［5］ Gschlobl S，Czado C．Spatial Modelling of Claim Frequency and Claim Size in Non－life Insurance［J］．Scandinavian Actuarial Journal，2007（3）．

［6］ Sun J F，Frees E W，Rosenberg M A．Heavy－tailed Longitudinal Data Modeling Using Copulas［J］．Insur．Math．Econ．，2008（2）．

［7］ Frees E W，Valdez E A．Hierarchical Insurance Claims Modeling［J］．Journal of the American Statistical Association，2008，103（484）．

［8］ Frees E W，Meyers G，Cummings A D．Dependent Multi－Peril Ratemaking Models［J］．Astin．Bulletin．，2010（2）．

［9］ Shi P，Frees E W．Dependent Loss Reserving Using Copulas［J］．Astin．Bulletin．，2011（2）．

［10］Czado C，Kastenmeier R，Brechmann E C，et al．A Mixed Copula Model for Insurance Claims and Claim Sizes［J］．Scandinavian Actuarial Journal，2012（4）．

［12］Nelsen R B．An Introduction to Copulas［M］．New York：Springer，2006．