基于目标导向的银行理财产品最优费率研究

李 峰，张 丛，龙建成

（1．西安电子科技大学a．经济管理学院；b．人文学院，陕西 西安 710071；

2．西安交通大学 经济与金融学院，陕西 西安 710061）

一、问题提出

近些年，借助自有销售渠道的优势，理财产品在银行中间业务中扮演了越来越重要的角色，其在提升银行利润的同时，也深刻地改变了人们的投资习惯。由于缺乏明文规定，众多商业银行在代售理财产品时，往往自行设定收费标准，导致理财产品的费率出现较大波动；同时出于隐性福利的考虑，银行对内部员工往往提供相比普通投资者更优惠的费率。费率的差异扭曲了理财产品的真实收益，无法客观反映理财产品的市场情况，由此影响了银行相关政策的制定，也不利于学者的系统性研究。

随着银行理财产品规模越来越大，探讨理财产品费率的优化已成为学者关注的重点。Grinblatt等运用期权定价理论，对基于业绩的费率结构进行了分析，由此开启了对最优费率的研究［1］。循着这一思路，Ou在时间连续的委托代理框架下，发现最优的费率结构应具有对称形式，包含一个固定的报酬加上一个超过基准收益所得的奖励或处罚［2］。Das等的研究却提供了一个相左的观点，认为相比于对称的费率结构，不对称的费率结构将产生帕累托占优的结果［3］。越来越多的学者加入了这场争论，如Cuoco等从实证角度研究了对称和不对称费率结构对资产均衡价格的影响［4］；Diao则走得更远，以中国为例，研究并检验了不对称费率结构对资产均衡价格的影响［5］。

二、模型的建立

本文探索融合银行的经济功能和社会功能，基于实现如下目标而设定银行理财产品费率：一方面提升银行的经济效益，毕竟银行是企业，追逐利润是其天性；另一方面也希望购买理财产品的投资者能增加收益，只有这样银行才能获得更好的社会效益。

首先分析理财产品投资者的行为特征。投资者购买理财产品的目的是追求自身经济效益的最大化，投资者效益函数如下：

其中λ衡量投资者购买理财产品的热情，设0≤λ≤1，g（λ）是投资者的收入函数。投资者购买理财产品的热情越高，越倾向于学习投资知识，相对来讲其盈利能力越强，本文合理假设g（λ）＝dλh，其中d、h为投资者的收入函数指标，反映投资者的学习能力等状况，d＞0，h＞0。由于学习存在边际效率递减效应，则g′（λ）＞0，g″（λ）＜0。y（λ）是投资者的成本函数，投资者购买理财产品的热情越高，其付出的成本也将越大（相关投资知识的培训、购买理财产品的费用等）。设y（λ）＝aλb，a、b为投资者的成本函数指标，反映理财产品的相关制度建设情况，a＞0，b＞0。同时设y′（λ）＞0，y″（λ）＞0，表明边际成本递增。

投资者追求自身经济效益的最大化，可表示为：

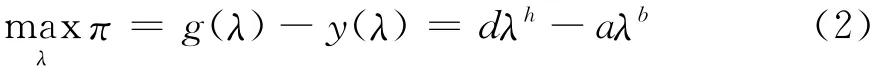
对投资者而言，d、h、a、b都是固定值，通过极值可唯一确定变量λ值：

即投资者购买理财产品的热情是综合考虑了投资者的收入函数指标（d、h）和成本函数指标（a、b）。

在银行追求经济效益最大化和综合效益最大化的两个假定下，下面分析不同目标导向下理财产品费率设定的模式。

（一）银行（单纯考虑经济效益）

银行通过调整理财产品费率，提升的利润为：

其中t为银行调整后的理财产品费率，0＜t＜1，t0为银行现有理财产品费率，P为理财产品的平均市场价格，Q为单家银行投资者购买的平均理财产品数量。设：

其中e为有效投资系数，L表示在一家银行购买理财产品的平均投资者数量，e与L的乘积决定了有效投资者的平均数量。随着投资者数量的增长，购买理财产品的数量也将增长，但增长的速度将变缓，合理假设F′（L）＞0，F″（L）＜0；有效投资系数e为：

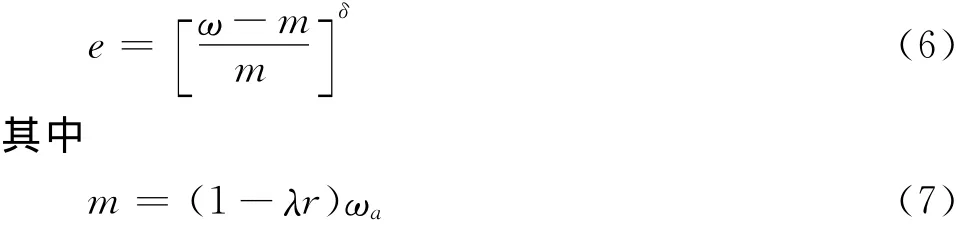
式（6）用费率调整后的预期收益率差来衡量有效投资系数e。ω是费率调整后的理财产品预期收益率；m是现有费率下的理财产品实际收益率；δ为购买理财产品收益的弹性系数，0＜δ＜1；r是家庭成员规避购买理财产品的意向；ωa为现有费率下的理财产品名义收益率；λ如前所设，衡量投资者购买理财产品的热情。由于社会上对购买理财产品存在一些看法，家庭成员的反对将稀释掉投资者的理财产品名义收益率，本文通过（1－λr）ωa将费率调整前的理财产品名义收益率ωa转化为实际收益率m（实际收益率可理解为名义收益率扣除与家庭成员的沟通成本，消除他们的抵触情绪后的剩余部分。当家庭成员支持购买理财产品时，规避购买理财产品的意向r为0，则m＝ωa，此时名义收益率即为实际收益率）。由式（6）和（7）可知，λ越大，有效投资系数e也越大，符合前文λ衡量投资者购买理财产品热情的假设。为了分析需要，设家庭成员规避购买理财产品的意向与调整后的理财产品费率成线性正相关关系，令：

其中r0为家庭成员规避购买理财产品的基本意向（当调整后的理财产品费率为0时，基于风险厌恶的假设，家庭成员对购买理财产品会存在抵触情绪r0），c为家庭成员规避购买理财产品的意向r对费率t的相关系数，定义c＞0。结合F′（L）＞0，F″（L）＜0的假设，把式（5）描述为：

其中α衡量投资者的交易意愿，β为理财产品购买数量的弹性系数。前文已假设L表示在一家银行购买理财产品的平均投资者数量。一般而言，银行设定的理财产品费率越高，则购买理财产品的投资者数量越少，合理假设L（t）同t呈反向关系：

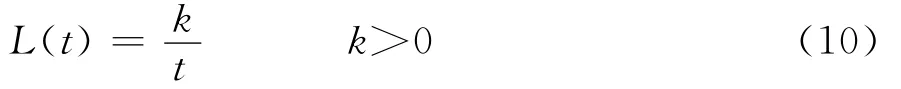
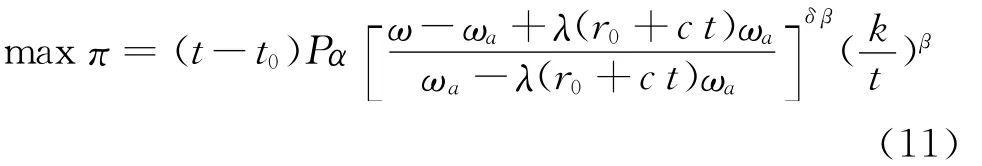
其中P是理财产品的平均市场价格。相对于银行而言，理财产品多为代销，P可视为定值。ω、ωa、r0、α、c、δ、β、k等指标对银行而言皆为外生变量，易得式（11）为t的递增函数，由此得出：

命题1：单纯考虑经济效益时，银行将调高理财产品费率。

（二）银行（综合考虑经济效益和社会效益）

当银行出于提升自身利润和增加投资者收益的目标而设定理财产品费率时，分析如下：

目标一：银行通过设定理财产品费率，提升自身利润，经济效益为：

目标二：银行通过设定理财产品费率，增加投资者收入，社会效益为：

k为衡量投资者数量与新设定的理财产品费率关系的相关指标。银行追求利润最大化，结合式（4）、式（6）～（10），其目标函数为：

结合两个子目标，则银行综合目标提升程度为：

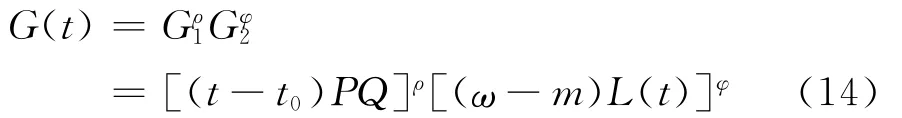
其中0＜ρ＜1，表示银行对通过设定理财产品费率，提升银行利润的偏好程度；0＜φ＜1，表示银行对通过设定理财产品费率，增加投资者收入的偏好程度，ρ＋φ＝1。结合式（6）～（10）、（12）、（13），式（14）转化为式（15）：

在t∈（0，1）这一开区间内，G（t）为连续函数，银行综合目标提升程度与费率的关系曲线可分为如下三种情形：

情形1：当t＝t0时，ω＝ωa（1－λr0－λct0），G（t）－t曲线与t轴有一个交点t0，如图1所示（不在定义域内的曲线用虚线表示，下同）。

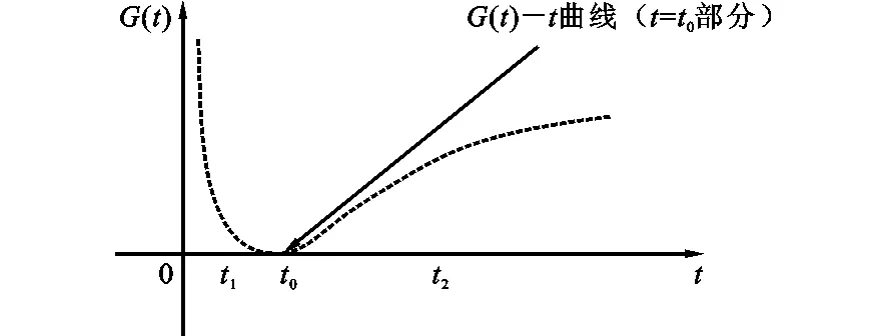
图1 银行综合目标提升程度G（t）－理财产品费率t（情形1）关系图

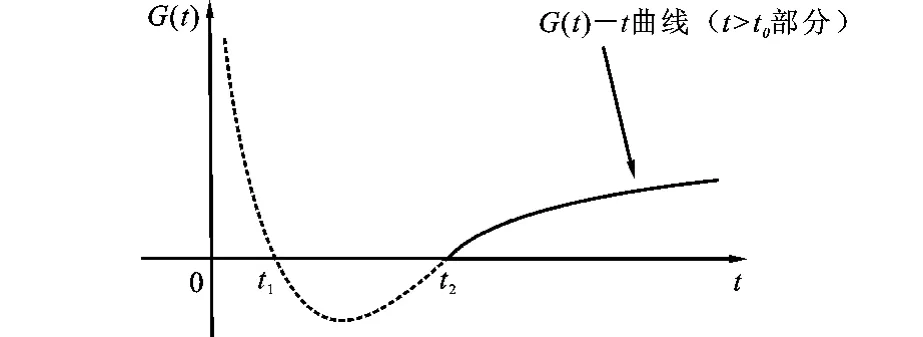
图2 银行综合目标提升程度G（t）－理财产品费率t（情形2）关系图

情形3：当0＜t＜t0

时，ω＝ωa（1－λr0－λct），G（t）恒等于0。G（t）－t曲线与t轴在（0，t0）区间重合，如图3所示。

把图1、2、3的实线部分重叠，构成了银行综合目标提升程度G（t）与理财产品费率t总的关系曲线，即G（t）－t曲线，如图4所示。

需要特别注意的是，由式（15）可知，G（t）－t曲线中t0＜t＜1部分的单调性是不确定的，取决于ρ、δβ、φ之间的大小关系（由于ρ＋φ＝1，实际上取决于ρ与δβ或φ与δβ的大小关系）。

图3 银行综合目标提升程度G（t）－理财产品费率t（情形3）关系图

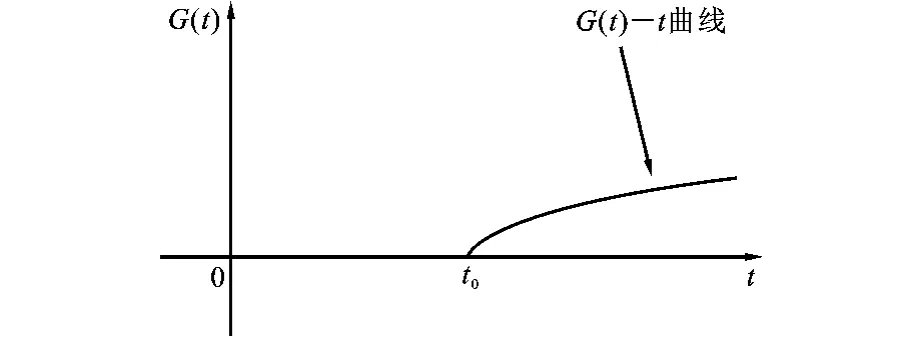
图4 银行综合目标提升程度G（t）－理财产品费率t总关系图

当费率t0＜t＜1时，无论ρ与δβ大小关系（决定了G（t）－t曲线中t0＜t＜1部分的单调性）如何，从图4易得，存在最优理财产品费率t＊，使得G（t＊）取得最大值。由式（15）可知t＊的大小取决于如下指标：银行现有理财产品费率t0、理财产品的平均市场价格P、投资者的交易意愿α、银行可选理财产品的最大预期收益ωmax、现有费率下的理财产品名义收益率ωa、投资者数量同银行费率关系的相关指标k、投资者购买理财产品的热情λ、家庭成员规避购买理财产品的基本意向r0、理财产品购买数量的弹性系数β、银行对通过调整理财产品费率提升银行利润的偏好程度ρ、银行对通过设定理财产品费率增加投资者收入的偏好程度φ、家庭成员规避购买理财产品的意向对费率的相关系数c以及购买理财产品收益的弹性系数δ，由此得出：

命题2：存在使银行综合目标提升程度最大的最优理财产品费率t＊。

结合命题2可知，t＊值将随着影响其大小的各项指标的变化而变化。银行需要在对经济形势客观把握的基础上，结合各项指标的变化情况，科学估计各个时点的t＊值，注重费率设定的针对性和灵活性，适时适度进行微调。综上可得：

命题3：最优理财产品费率t＊不是固定值，而是一个动态概念。

当费率在t0＜t＜1区间内，无论ρ与δβ大小关系（决定了G（t）－t曲线中t0＜t＜1部分的单调性）如何，从图4易得G（t）＞0恒成立，由此可得：

命题4：银行调高理财产品费率，将提升银行综合目标的实现程度。

当费率在0＜t＜t0内，G（t）＝G（t0）恒成立。无论银行如何调低理财产品费率，银行的综合目标实现程度不变，由此可得：

命题5：银行调低理财产品费率，并不会改变银行的综合目标。

三、研究设计

（一）数据来源

2006年至今，伴随资本市场的火爆，银行理财产品的发行也出现了井喷态势。根据WIND数据统计，2011年1至9月，存款性金融机构共发行银行理财产品14 751款，发行规模超过11万亿元。由于上市大银行比小银行在信息披露的公开和及时性方面更具优势，且收费的项目更加透明，较少隐性收费，由此本文选择工商银行作为研究对象，对其发行的理财产品进行了月度追踪，将其在2007年末至2012年9月发行的488款理财产品进行了统计。

本文从资产托管费率和销售手续费率两个维度，通过两者加总度量银行理财产品的总费率，这样做的实证结果更为全面和稳健。样本数据来源于工商银行官网。对官网并未披露信息的产品，则通过查阅产品说明书、Google网、公司关联企业的披露信息等途径进行了详细补充。按照以下原则对样本产品进行筛选：（1）剔除12款无固定期限的产品；（2）由于外币同人民币存在汇率结算问题，而目前汇率的变动巨大，剔除以外币结算费率的产品41款；（3）剔除无资产托管费和销售手续费的产品57款，需要注意的是，有11款理财产品同时具备上述（2）（3）两项特征，需要避免重复剔除。

表1为2007年末至2012年9月间工商银行发行的488款理财产品的统计分析。

表1 工商银行理财产品统计分析表

以半年为界限，半年以内（含半年）为短期理财产品，半年以上为长期理财产品。从表1中分析得知，3个月以内的理财产品出现了158次，占样本总数32．38%，3个月至半年的181次，占样本总数37．09%，两者合计占比69．47%，超过六个月的仅占30．53%，表明银行倾向于发行短期理财产品。原因在于样本分析期正值全球金融危机爆发期间，资本市场短期内的不确定性大大增强。对产品发行方而言，发行短期产品有利于规避市场风险；就投资者来说，短期理财产品占用资金时间短，有助于满足其对资金流动性的要求。

（二）描述性统计

表2是样本银行2007年末至2012年9月间理财产品总费率（资产托管费率和销售手续费率的加总）的描述性统计。从表2可以看出，488款理财产品总费率的最大值为1．785%，最小值则是0．12%，样本标准差为0．178 3%，这表明银行不同理财产品的费率差距较明显。应该指出的是，期限为4至6个月的短期理财产品，其费率间差距最小，标准差为0．087 3%。

表2 样本银行理财产品总费率的描述性统计表

（三）实证分析

同上，将不同期限的理财产品划分为不同区间，分别从理财资产托管费率、销售手续费率以及总费率角度分析理财产品费率的变化趋势。通过Excel对相关数据做趋势分析，表3列出了不同期限理财产品费率的变化趋势，“＋”号表示费率存在上升趋势，“－”号表示费率存在下降趋势。

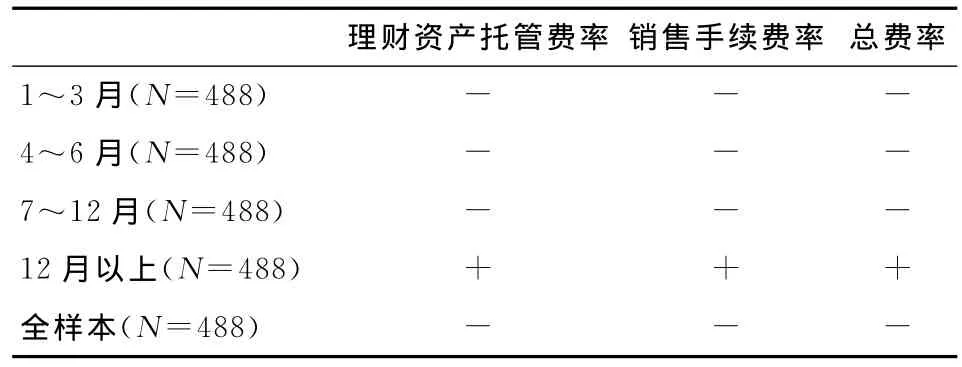
表3 样本银行理财产品费率趋势表

通过对表3的分析可以发现，样本银行对短期理财产品采取了降低费率的措施，而对长期产品则调高了费率，原因在于金融危机期间，理财产品在短期内的收益波动相对长期较为剧烈，银行需要通过降低费率，相对提高短期投资者购买理财产品的实际收益率，由此促进短期理财产品的发行。由命题1的推论过程可知，此时银行的经济利益受损。由命题5可知银行的综合目标并不受影响，这就意味着银行以牺牲自身经济效益的方式增加了投资者收入，通过社会效益的提升弥补经济效益的损失。同时，金融危机对经济的冲击毕竟是短暂的，结合命题1和命题4，银行在设定长期费率时，最优选择应是逐步调高理财产品费率，提升自身的经济效益和综合目标实现程度，这也符合实证结果。

四、结论和政策建议

理财产品规模的扩大引起了学者对理财产品费率的关注。本文通过对银行在不同目标下的行为分析，建立了一个银行目标导向型的理财产品费率设置模型，搭建了用于分析理财产品费率调整的框架。研究发现：投资者在结合学习能力、理财产品的相关制度建设情况后，决定自身购买理财产品的热情；银行作为费率的制定者，结合各项经济指标和需要达到的目标，设定其最优的理财产品费率，为分析中国银行理财产品的费率问题构建了一个分析框架。研究表明：单纯考虑经济效益时，银行将调高理财产品费率；存在使银行综合目标提升程度最大的最优理财产品费率；最优理财产品费率不是固定值，而是一个动态概念；银行调高理财产品费率，将提升银行综合目标的实现程度；银行调低理财产品费率，不会改变银行的综合目标。实证结果也显示，国内的大型银行已从对经济效益的单纯关注转向重视企业的社会责任，其制定相关收费标准的出发点已从经济视角转向综合目标实现程度的提升。全球金融危机爆发期间，为规避市场风险，银行倾向于发行短期理财产品，且降低了其相关费率。该措施削减了银行的经济效益，却有利于投资者的收入增加，综合考虑提升自身利润和增加投资者收益，银行的综合目标并未受到影响。此外，从长远角度考虑，经济的平稳增长将是一个常态，由此银行将调高长期理财产品的费率，追求自身综合目标更大程度的提升。

［1］ Grinblatt M，Titman S．Adverse Risk Incentives and the Design of Performance－Based Contracts［J］．Management Science，1989，35（7）．

［2］ Ou Yang Hui．Optimal Contracts in A Continuous－Time Delegated Portfolio Management Problem［J］．The Review of Financial Studies，2003，16（1）．

［3］ Das Sanjiv R，Rangarajan K．On the Regulation of Fee Structures in Mutual Funds ［R］．New York：New York University Working Paper，1998．

［4］ Cuoco Domenico，Ron Kaniel．Equilibrium Prices in the Presence of Delegated Portfolio Management［J］．Journal of Financial Economics，2001，101（2）．

［5］ Diao Xifeng．Asymmetric Fund Manager Compensation and Equilibrium Asset Pricing：Theory and Evidence from China［R］．Vancouver：University of Brithish：Lolumbia Working Paper，2003．