基于AHP的范例推理在黄土边坡稳定性中的应用

赵秋鹏

(西北大学地质系，陕西 西安 710069)

式中:maxxj，minx为源范例中第 j个属性的最大值和最小值。

在我国西北地区，黄土面积分布广，厚度大，沟壑十分发育。地表被纵横交错的大小冲沟切割得支离破碎，使得其两侧的边坡也形态各异，黄土边坡往往具有较陡的坡度，常年受降水侵蚀及风化等因素的影响，裂隙发育，有的处于稳定状态，有的则由于存在不良地质体，或人工改造，则处于不稳定或潜在的不稳定状态，然而越来越多的铁路、高速公路工程修建于黄土地区［1］。因此，当线路穿过上述地段，这就对黄土边坡的稳定性提出了很高的要求。

当前对边坡稳定性的分析和研究的方法颇多，比如工程地质类比法、力学分析法等，同时随着模糊数学理论、灰色系统理论和可靠度理论等引入，边坡稳定性评价已不限于单一一种理论或方法的运用，而是朝着多种方法综合运用的方向发展。然而实际工程中限于工期与投资，对大量的黄土边坡不可能进行详细的勘察和单独的稳定性评价，工程上迫切需要一种简单适用的黄土边坡稳定性评价方法［2］。针对影响边坡稳定性的诸多因素的不完整性和不确定性，本文利用基于AHP的范例推理方法，建立黄土边坡稳定性评价模型。

1 基于AHP的范例推理的评价模型

范例推理(Case－Based Reasoning，简称CBR)是由Roger Shank在1982年提出的，Janet Kolodner开发第一个CBR系统CYRUS，将CBR理论引入了人工智能领域的研究中来［3］。范例推理是指利用过去经历的典型事例(称为范例)求解或理解当前问题，又称为“即时推理”［4］。其工作原理是模仿人们的认知心理过程［5］，它是由目标范例的提示而得到历史记忆中的源范例，并由源范例来指导目标范例求解的一种策略。范例推理广泛应用与机械设计、医疗诊断、农业、气象等领域，并取得了良好的成果。范例推理中是以范例为基础，范例中知识的获取需要全面的去把握，考虑问题整体化。对于黄土边坡稳定性的研究这样的复杂问题，其影响因素是多方面的，更需要站在全局的角度去理解这个问题，所以范例推理为黄土边坡稳定性的研究提供了一条可行的新思路［6］。

1.1 黄土边坡范例库的建立

范例知识的表达就是把已有的知识或者经验表示成一个范例库，CBR在此基础上才能发挥作用。收集已研究清楚且稳定状况有明确结论的众多黄土路堑高边坡实例，收集黄土边坡资料数据，构建边坡稳定性评价的源范例库［7］。其中范例库中每条记录就是一个范例(边坡实例)，每个字段就是范例的一项属性(如边坡容重、坡高、坡度、内摩擦角和粘聚力等)。

1.2 属性权重的确定

权重用来衡量各影响因素的相对重要性。在工程综合评价中，权重计算的方法较多，主要有专家咨询法、主成分分析法、AHP、熵值法、因子分析法和人工神经网络法等，这里我们运用AHP来计算各影响因素的权重。层次分析法［8］是美国数学家T.L.Saaty于1980年首次提出的一种比较简单可行的决策方法，其主要优点是可以解决多目标的复杂问题、定性与定量相结合的决策分析方法，它可以为决策者提供多种决策方法，在定量和定性相结合中根据各个决策方案的标准权重数来判断决策方案的优劣，它能有效地解决很多难以完全用定量或定性方法解决的实际问题。

建立判断矩阵，从层次结构模型方案层开始，对于从属于上一层的每个因素的同一层诸因素进行两两比较，比较其对于准则的重要程度，并按事前规定的标度定量化，计算权向量［9］。

对每一个成对比较矩阵，利用求和法计算最大特征根及对应特征向量:

(1)对成对比较矩阵A的每一列向量进行归一化，得:

(2)对w'ij按行求和，得:

(3)将w'ij归一化，得w=(w1，…，wn)T，即为近似特征向量，

(4)计算最大特征根的近似值。

并计算一致性检验:AHP要求判断矩阵具有大体的一致性，能够使计算的结果基本上合理。对矩阵进行一致性检验，计算

式中:RC为一致性比率。当 RC＜0.1时，认为不一致程度在容许范围之内，而

式中:λmax为一致性矩阵的最大特征根，n为成对比较的因子的个数;IR为随机一致性指标，其值由下表1确定。

表1 随机一致性指标IR值

1.3 范例间的相似性计算

目标范例与源范例的比较是通过相似性计算进行的。常用的范例推理模型有基于欧氏距离、曼哈顿距离和模糊相似优先的范例推理。本文采用欧氏距离来计算目标范例与源范例的相似性。欧氏距离计算公式为:

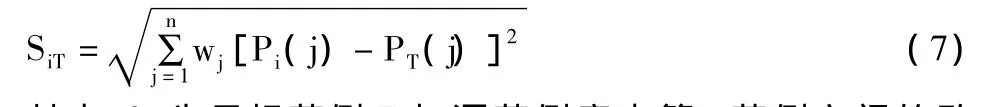
其中:SiT为目标范例T与源范例库中第 i范例之间的欧几里德距离。SiT越小，说明它们之间越相似;wi为边坡第 j个影响因素的属性权值;Pi(j)为源范例库中第i个范例的第j个属性的值;n为属性总数;Pi(j)为目标范例 T的第 j个属性的值。

同时在进行相似度计算时，考虑到各属性参数的量纲不同，具有不可公度性，采用式对各属性参数进行规范化处理，将各属性值变换到［0，1］区间。

式中:maxxj，minx为源范例中第 j个属性的最大值和最小值。

2 工程实例分析

调查并收集山西吕梁、陕西咸阳等地的黄土边坡资料数据，提取其中具有代表性的20个作为研究对象进行分析，其中前16个作为源范例，后4个作为目标范例。影响因素分别为边坡坡高(H)、坡度(α)、容重(γ)、内摩擦角(Φ)和粘聚力(C)，共5个。边坡有2类状态，即稳定和破坏，见表2。

2.1 数据处理

因为每个属性的量纲不同，因此，采用式(8)对中的原始数据进行归一化处理，结果见表3。

2.2 权重的计算

根据1～9标度法，构造判断矩阵:

再根据(1)—(6)式计算，得 λmax=5，由于 λmax

是整数，RC=0＜0.1，则必然通过矩阵的一致性检验，那么矩阵归一化后的特征向量就是各因素的权重值，即:

w=(0.0435，0.3478，0.3478，0.0870，0.1739)T

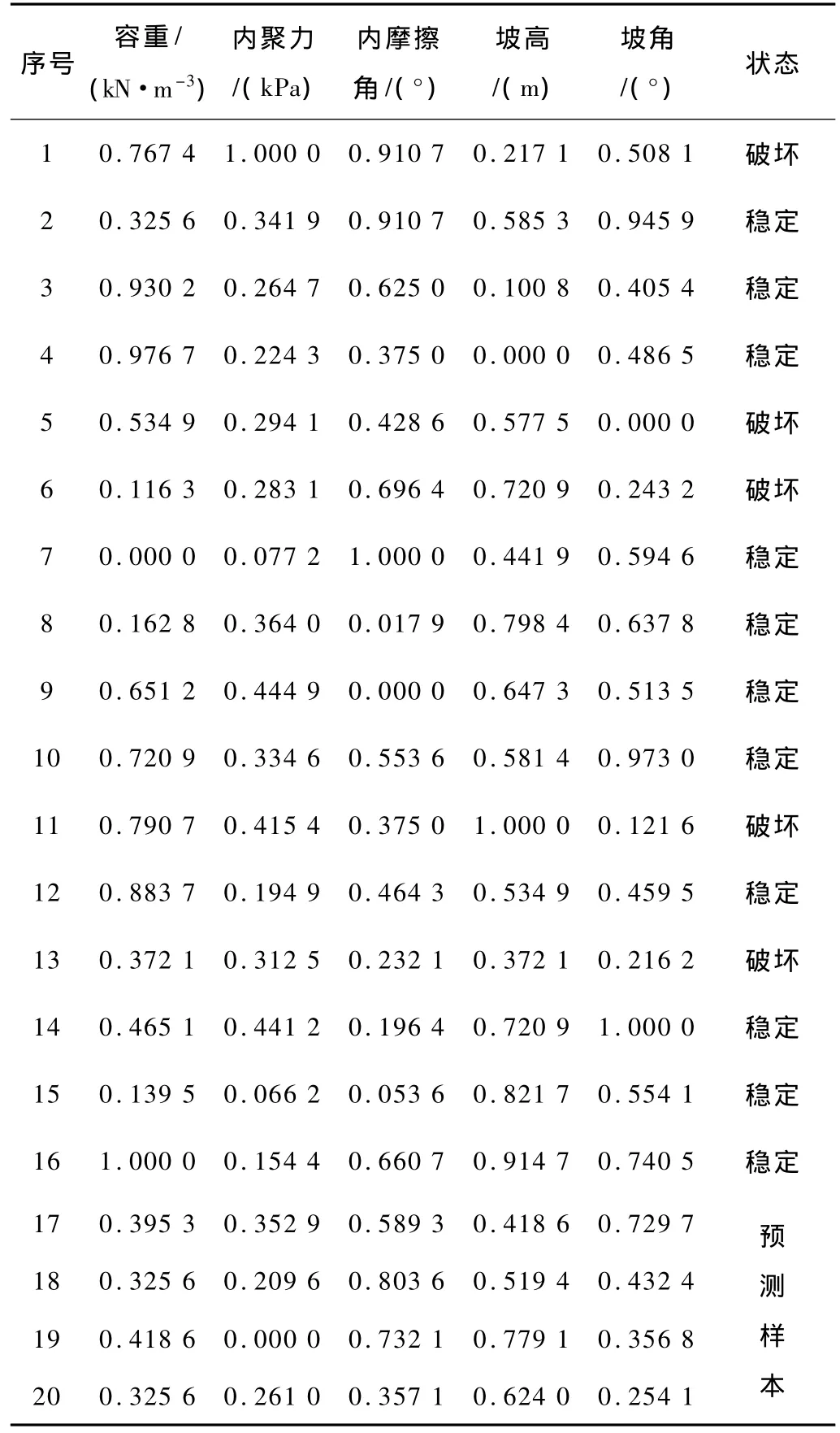
表2 边坡实例及稳定状况

由表可知，目标范例17与源范例10最相似;目标范例18、19都与源范例6最相似;目标范例20都与源范例13最相似。而源范例10、6、13处于稳定、破坏、破坏状态，所以，目标范例17处于稳定状态，18、19和20都是处于破坏状态，经实际调查，这些与实际状态相符。

表3 工程实例数据的归一化处理结果

2.3 目标范例与源范例之间的相似度计算

根据(7)式可求得范例间的相似度，如下表4:

3 结语

(1)本文将AHP运用到范例推理方法中，对其进行权重上的优化，然后再通过已被研究清楚的边坡的成功经验对将要研究的边坡状态进行正确评价。实例分析表明，该方法原理简单、评价结果可靠，是一种黄土边坡稳定评价的可行性的方法。

(2)当然，本文的黄土边坡AHP与范例推理相结合的评价方法的研究工作尚有许多不成熟和不完善的地方，还有许多理论和应用问题有待进一步的研究探索和提高。比如搜集的边坡案例较少，在一定程度上影响了范例推理方法的应用范围与效果;边坡的影响因素仅考虑的5种(容重、内摩擦角、粘聚力、坡高和坡度)，而实际上边坡的影响因素还有很多，如降雨、植被覆盖、边坡类型、人类活动等:边坡的状态仅考虑了稳定和破坏两种，考虑过于简单，因为在实际中许多边坡处于中间状态，应该进一步细化，使之更加的接近实际状况。

表4 目标范例与源边坡范例的相似度序列

［1］张庆飞.黄土地区隧道洞口段边坡稳定性研究［D］.西南交通大学大学硕士研究生学位论文.2005.

［2］赵文，贺玉龙.基于范例推理结构型岩体边坡稳定性评价［J］.铁道工程学报.2008，7(118):5 －9.

［3］Kolodner J L.Improving human decision making through case－based reasoning techniques［J］. AIMagazine，1991，12(3):52 ～ 59.

［4］杨善林，倪志伟.机器学习与智能决策支持系统［M］.北京市:科学出版社.2004.

［5］Lenz M.Case－based reasoning:from foundations to applications［M］.Berlin:Springer，1998.

［6］刘沭宇.基于范例推理的边坡稳定性智能评价方法研究［D］.武汉理工大学博士学位论文.2001.

［7］高德彬，倪万魁，郭社锋.基于范例推理的黄土路堑高边坡稳定性预测研究［J］.工程地质学报.2007，15(5):635－638.

［8］姜启源.数学模型(第二版)［M］.北京:高等教育出版社.1993.

［9］樊晓一，乔建平，陈永波.层次分析法在典型滑坡危险度评价中的应用［J］.自然灾害学报.2004，13(1):72 －76.