铁路桥梁承载能力可靠性分析
徐升桥,彭岚平,侯建军,简方梁,赵博,李圣强
(中铁工程设计咨询集团有限公司,北京 100055)
当功能函数采用最简单的形式Z=R-S时,假定R与S相互独立,服从正态分布,均值和方差分别为μR、μS、σR、σS。根据概率论的相关知识,Z 同样服从正态分布,其均值μZ和方差σZ可表达为
1 概述
结构可靠度通常被定义为:结构在规定的时间内、在规定的条件下,完成预定功能的概率。结构的可靠度分析与结构的极限状态方程相联系,通常结构的功能函数表达为
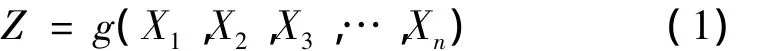
式中,Xi为随机变量,指影响结构抗力与荷载效应的各种因素。当Z>0时,表示结构处于可靠状态;Z=0时处于极限状态;Z<0时处于失效状态。
结构的失效概率可通过如下积分求得
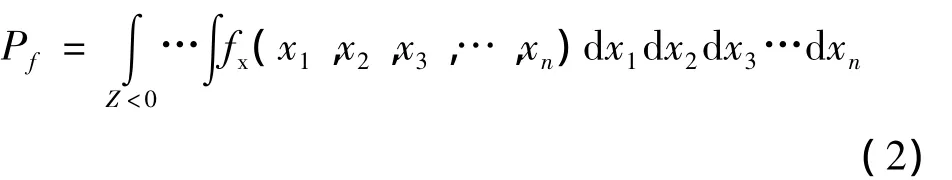
当功能函数采用最简单的形式Z=R-S时,假定R与S相互独立,服从正态分布,均值和方差分别为μR、μS、σR、σS。根据概率论的相关知识,Z 同样服从正态分布,其均值μZ和方差σZ可表达为
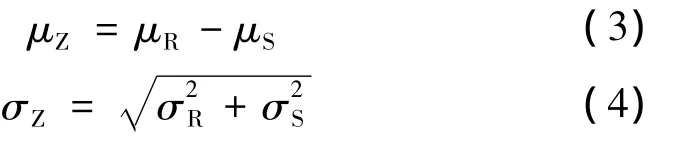
结构的失效概率可等效表达为

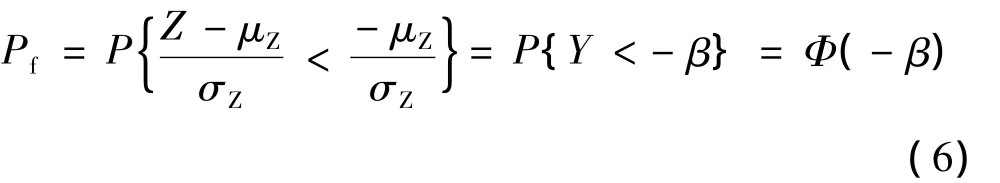
式中,Y为标准正态随机变量;Φ()为标准正态分布函数,上式中β值与结构的失效概率一一对应,称之为可靠度指标,它表达的几何意义为标准正态分布函数中均值距零点的距离。
由式(2)可知,当结构功能函数较多时,结构的失效概率为一多变量函数在复杂空间区域的高维积分,求解相当困难,而由前面的简单推导,可知道当功能函数中的各变量为相互独立的正态分布随机变量时,结构的失效概率与可靠度指标有一一对应关系,因此,目前通常采用计算可靠度指标从而间接得到结构失效概率的方法。这种方法隐含功能函数必须为正态分布的条件,通常具有近似性,但是当采用比较好的近似方法时,仍然能够得到较为准确的计算结果。
2 工程可靠度求解常用近似方法
目前可靠度计算存在多种理论,主要包括一次二阶矩法[1]、蒙特卡罗法[1]、响应面法[1]等,应用最为广泛的为一次二阶矩法,包括均值一次二阶矩法(中心点法)、改进的一次二阶矩法(验算点法)。
一次二阶矩法的基本思想可概括为:将功能函数Z=g(X1,X2,X3,…,Xn)在某一点 Taylor级数展开,忽略高阶项,然后利用基本变量的一阶矩及二阶矩求得Z的均值及方差。中心点法与验算点法的差别主要体现在展开点的不同。
2.1 中心点法
中心点法将功能函数在各均值点展开,形成的功能函数的近似值如下Z ≈ g(μX1,μX2,μX3,…,μXn)+
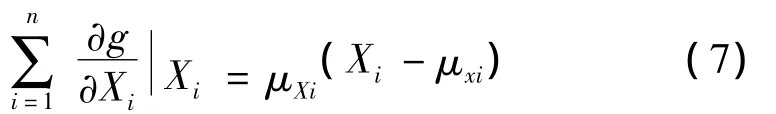
可得Z的均值与方差分别为
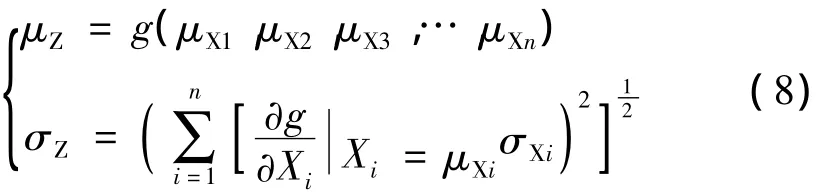
从而得到结构的可靠度指标为
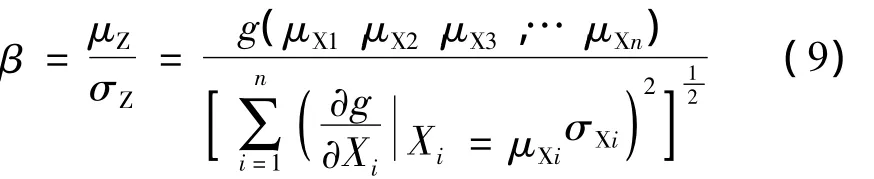
中心点法的最大优点是计算简便,只需知道基本变量的均值与方差,即可求得功能函数的可靠度指标;存在的主要问题:对于同一结构构件的同一功能需求,采用不同的功能函数,所得可靠度指标可能不同;另外,功能函数在均值点展开可能带来较大的误差。
2.2 验算点法
针对中心点法的不足,验算点法将展开点取为对结构最不利的各随机变量的取值点,设验算点的坐标为 m=(X*1,X*2,X*3,…,X*n),则
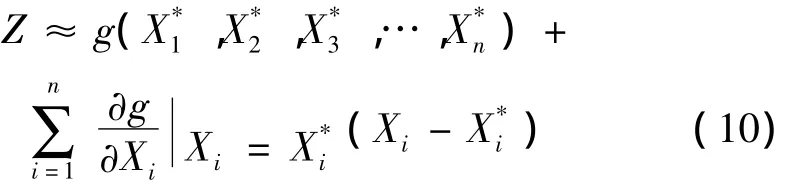
则Z的均值与方差为
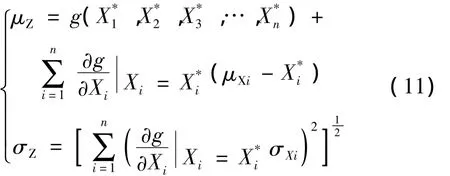
结构的可靠度指标表达为
对于若干相互独立的正态分布随机变量,验算点位于极限状态曲面上,在原坐标系的坐标应为
式中,αi为灵敏度系数,意义为第i个随机变量对整个标准差的影响,表达如下
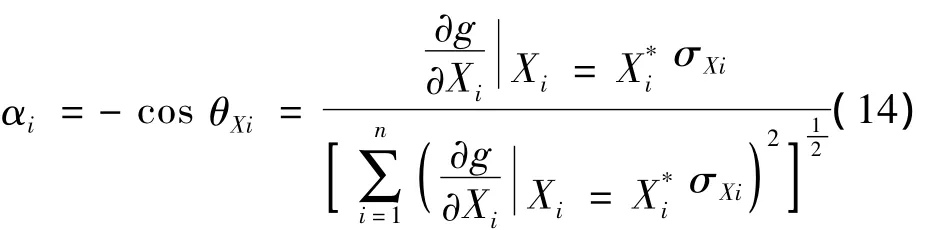
通过式(11)~式(14)的不断迭代,最终使得m点位于极限状态曲面上,求得β值,验算点法将展开点取在极限状态曲面上,提高了β值的计算精度,并且保证了对同一结构β值的唯一性。
2.3 可靠性指标β值计算程序
为了方便研究人员计算按现行“铁路桥规”(TB10002)设计的桥梁结构的β值,采用C++语言编制了基于中心点法和验算点法的β值计算程序(图1),共考虑了4种功能函数。
3 混凝土桥梁正截面抗弯承载力可靠度指标
3.1 正截面抗弯承载能力功能函数

式中 MR——构件能够承担的截面弯矩;
MS——荷载产生的截面弯矩。
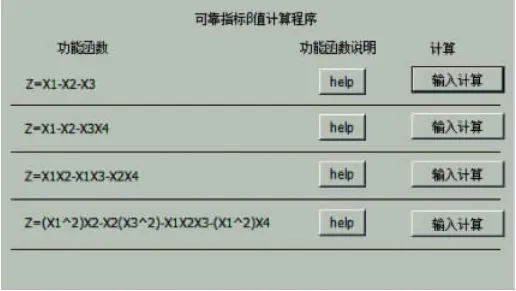
图1 可靠性指标β值计算程序界面
3.2 荷载
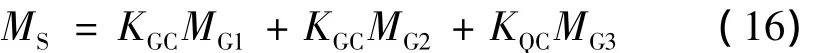
式中 KGC——恒载计算模式不定性系数,N(1,0.072);
KQC——活载计算模式不定性系数,N(1.0,0.102);
MG1——一期恒载产生的弯矩;
MG2——二期恒载产生的弯矩;
MG3——列车活载产生的弯矩。
(1)恒载
桥梁恒载与设计值之比服从正态分布(表1)

表1 恒载参数统计值
(2)列车活载
服从对数正态分布,列车活载考虑偏差、超载、冲击的影响

式中 Kh——列车竖向静载模型不确定性系数,N(0.961 86,0.037 132);
Ks——偏载系数,服从三角分布,数学期望值为1.0,均方差为0.013 01;
Kμ——动力系数,N [(1.00+1.176/(-0.2)),(0.024+0.22/(-0.2))2];
Mh——列车活载弯矩。
3.3 抗力
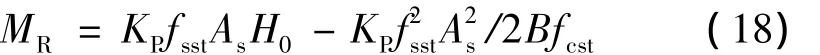
式中 KP——抗力计算模式不定性系数;
fsst——钢筋的抗拉强度;
fcst——混凝土轴心抗压强度;
As——受拉钢筋面积;
B——混凝土截面上翼缘计算宽度。
混凝土、预应力筋、梁体几何尺寸的统计参数见表2~表4,计算不定性系数服从正态分布,其均值为1.05,变异系数为0.064 7。

表2 混凝土轴心抗压强度统计参数

表3 预应力筋抗拉强度统计参数

表4 梁体几何尺寸统计参数
3.4 可靠度指标计算结果
现行铁道部预应力混凝土梁通用参考图的β值计算结果见表5。
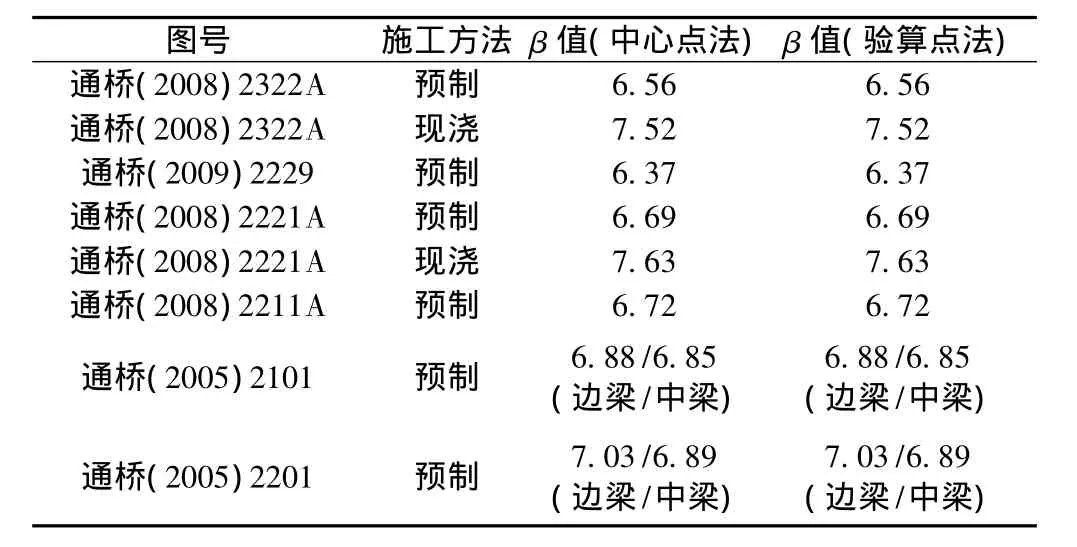
表5 正截面抗弯承载力可靠度指标(32 m跨度)
4 钢梁承载力可靠度指标校核
极限状态方程为

式中 R——杆件抗力,服从对数正态分布;
D——恒载引起的杆件内力,服从正态分布;
Qh——活载引起的杆件内力,服从对数正态分布;
η——活载发展系数。
近年设计的下承式道砟桥面简支钢桁梁跨度、结构形式见表6,表7~表13中、V和σ分别为各随机变量的均值、变异系数和均方差。

表6 下承式道砟桥面简支钢桁梁跨度、结构形式
(1)64 m单线钢桁梁概图见图2,杆件β计算结果见表7。
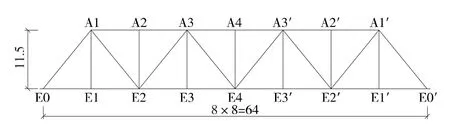
图2 64 m单线有竖杆三角桁架结构(单位:m)
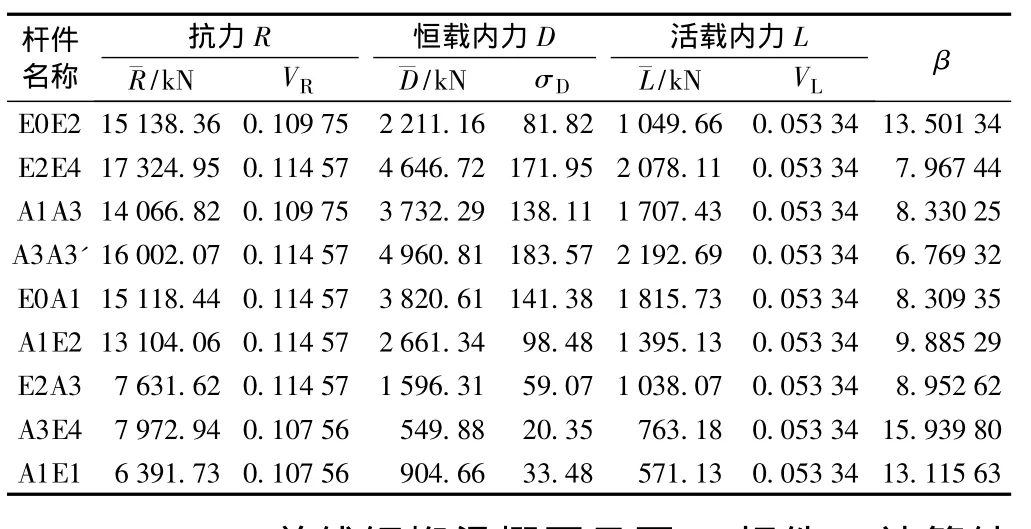
表7 64 m单线钢桁梁杆件β值
(2)80 m单线钢桁梁概图见图3,杆件β计算结果见表8。
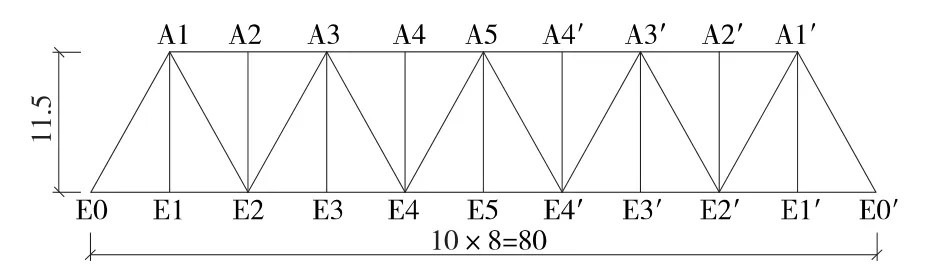
图3 80 m单线有竖杆三角桁架结构(单位:m)
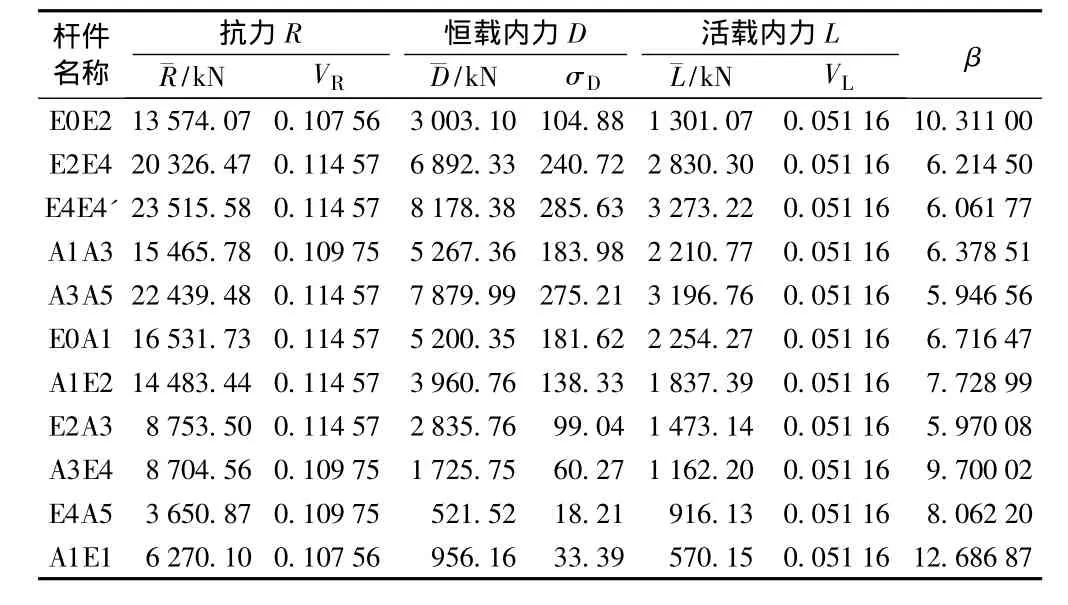
表8 64 m单线钢桁梁杆件β值
(3)64 m双线钢桁梁概图见图4,杆件β计算结果见表9。
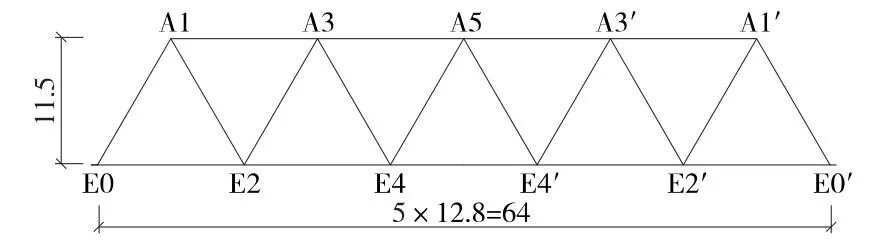
图4 64 m双线无竖杆三角桁架结构(单位:m)
(4)80 m双线钢桁梁概图见图5,杆件β计算结果见表10。
(5)80 m双线重载钢桁梁概图见图6,杆件β计算结果见表11。
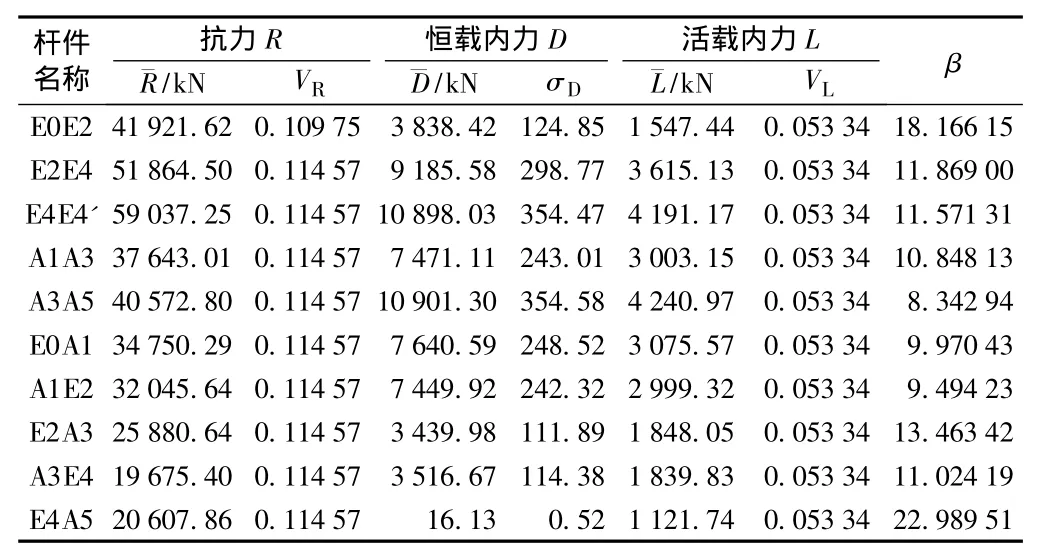
表9 64 m双线钢桁梁杆件β值
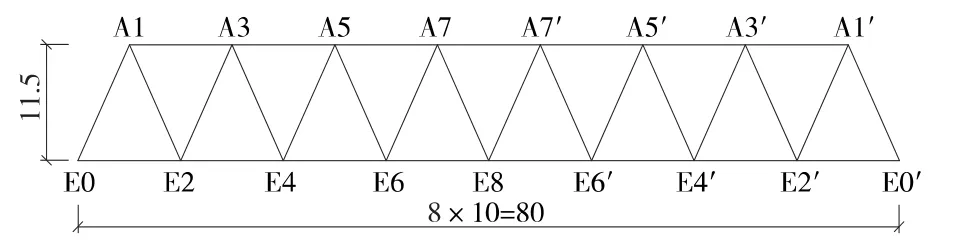
图5 80 m双线无竖杆三角桁架结构(单位:m)
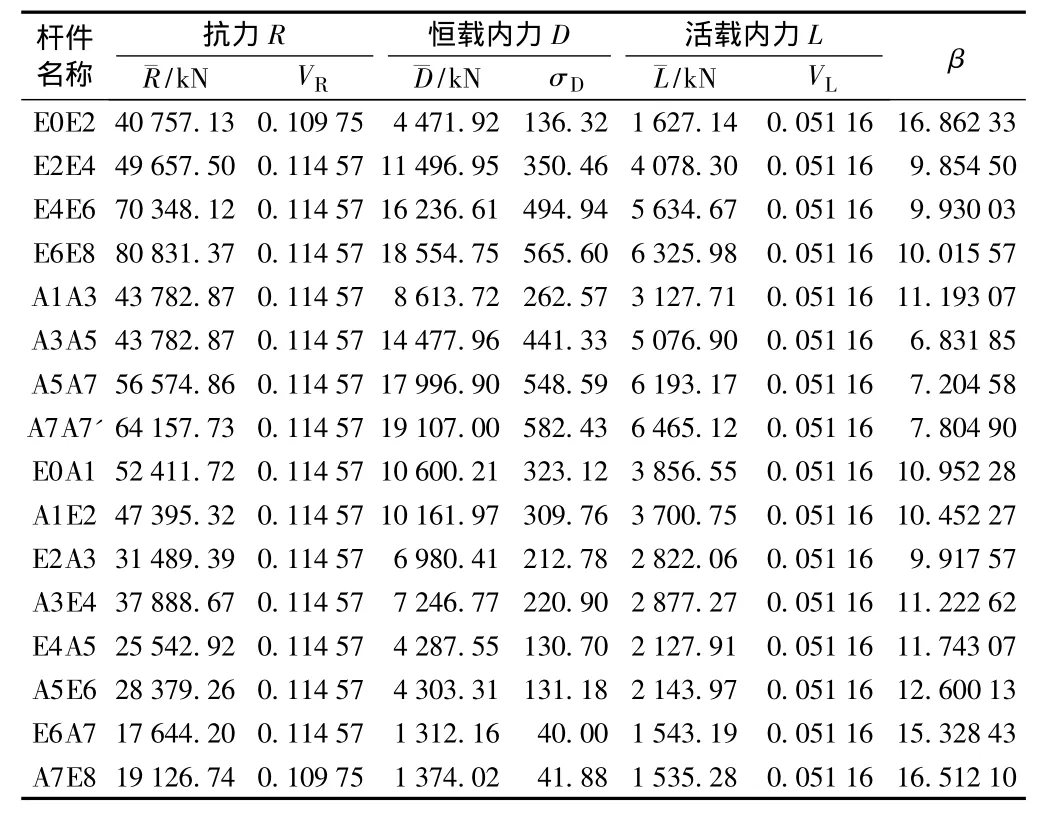
表10 80 m双线钢桁梁杆件β值
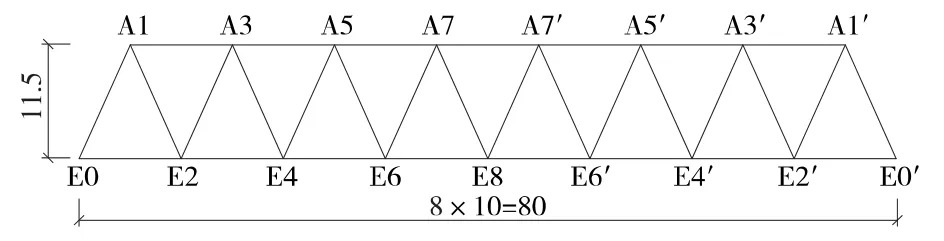
图6 80 m双线重载无竖杆三角桁架结构(单位:m)
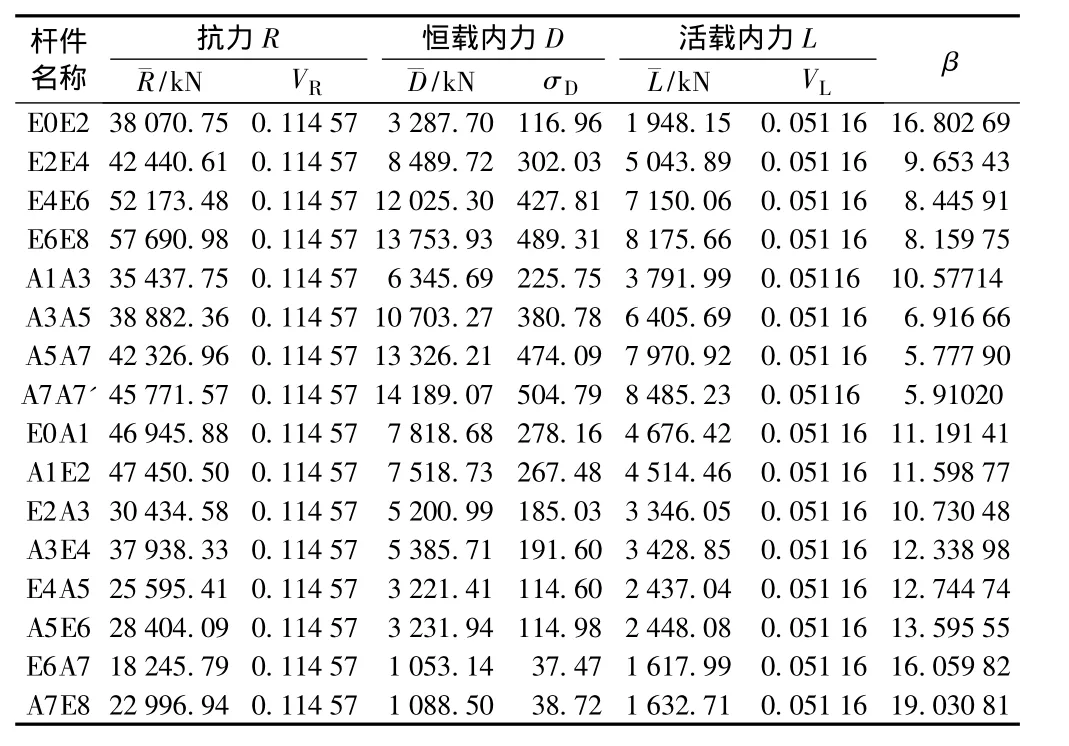
表11 80 m双线重载钢桁梁杆件β值
(6)96 m双线重载钢桁梁概图见图7,杆件β计算结果见表12。
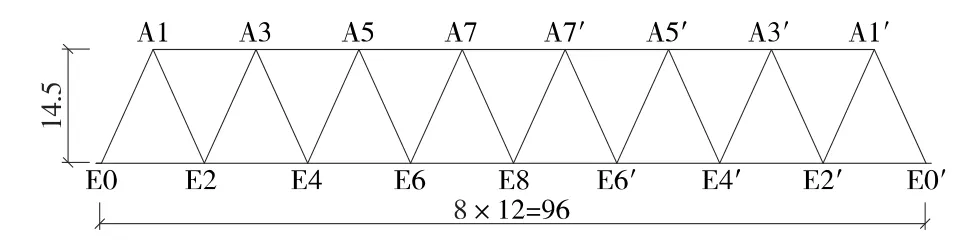
图7 96 m双线重载无竖杆三角桁架结构(单位:m)
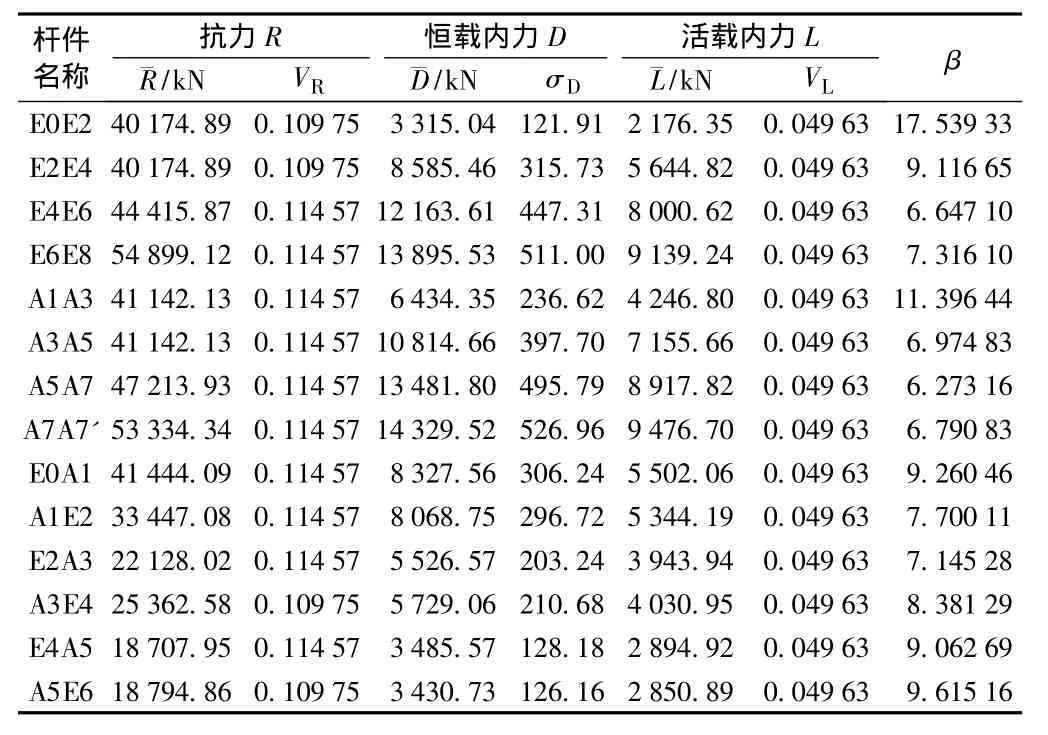
表12 96 m双线重载钢桁梁杆件β值
(7)128 m双线重载钢桁梁概图见图8,杆件β计算结果见表13。
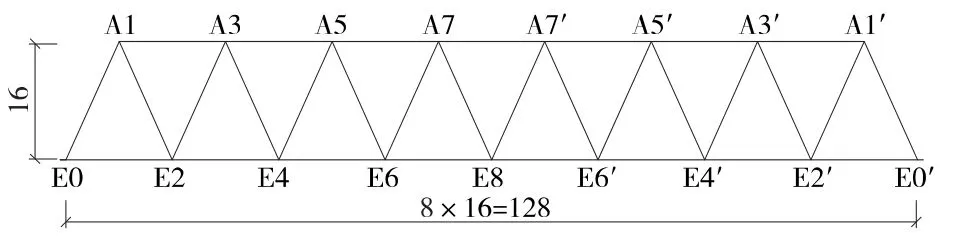
图8 128 m双线重载无竖杆三角桁架结构(单位:m)

表13 128 m双线重载钢桁梁杆件β值
5 钢-混结合梁承载力可靠度指标校核
钢-混结合梁桥的计算模式不定性系数KΩR取值:计算弯矩时 UΩR=1.03、VΩR=0.05,计算剪力时 UΩR=1.03、VΩR=0.11。
选取时速250 km客货共线铁路上承式简支结合梁(双线)(图号:专桥(2011)0225—Ⅵ)和时速250 km客运专线有砟轨道钢-混凝土连续结合梁(双线)图号(通桥(2005)0243)来计算跨中弯矩和支点处剪力的β值。跨度分别为40 m和(32+48+32)m,钢和混凝土结合前后的主梁跨中弯矩及支点处剪力的β值见表14、表15。
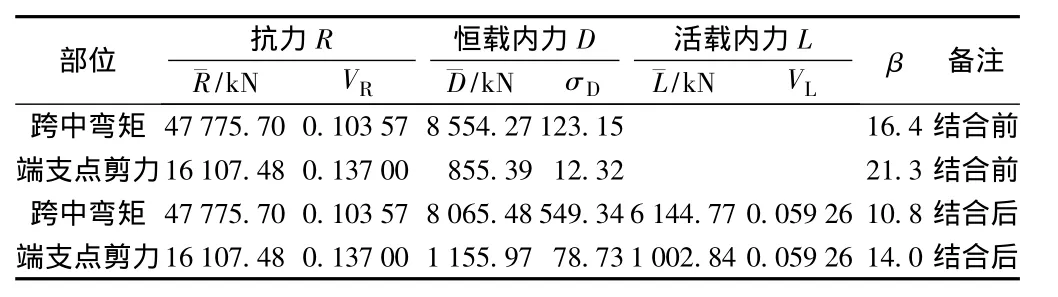
表14 40 m简支钢-混结合梁β值
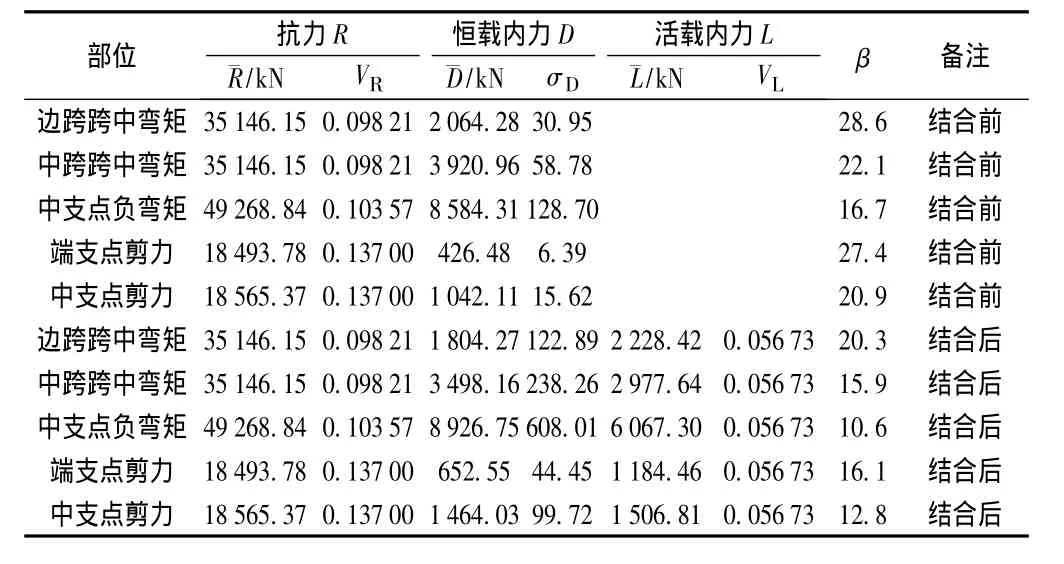
表15 (32+48+32)m连续钢-混结合梁β值
6 钢管混凝土结构承载力可靠度指标
6.1 轴心受压、纯弯构件功能函数
根据《铁路桥梁钢管混凝土结构技术规程》[1],轴压下的强度计算公式为

相应钢管混凝土构件轴压可靠度指标的功能函数可表达为

式中,N为荷载产生的效应,当仅考虑自重、二期恒载等恒载效应及列车活载效应时,上式可进一步改写为
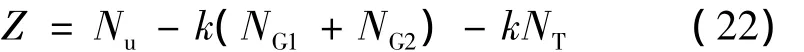
式中,NG1为自重效应产生的轴压效应,NG2为二期恒载产生的轴压效应,NT为列车活载产生的轴压效应。
对于纯弯构件,只需将上述公式中的轴力用弯矩代替即可。
6.2 工程实例计算
鄂尔多斯铁路机场线乌兰木伦河特大桥基本结构形式为(54+60+54)m、(60+72+60)m三跨钢管混凝土空间桁架组合连续曲梁(图9),曲线半径为700 m。结构采用钢管混凝土与混凝土桥面板通过腹杆连接形成空间受力体系。桥面至钢管混凝土中心高5.2 m,一个节间为6 m,桥面板宽12.6 m。下弦杆为单根钢管混凝土,管外径1.2 m,管壁厚在中间支点左右一个节间范围内为60 mm、其他区域为50 mm;腹杆采用工字钢,工字钢的断面根据受力需要分为3种形式;桥面板中间板厚350 mm,与腹杆相接处局部加厚至900 mm,腹杆支承外侧悬臂3.4 m。桥面板通过施加纵向及横向预应力保证受力安全。腹杆与下弦钢管混凝土之间采用节点板栓接,腹杆与桥面板之间采用剪力钉连接。主梁横断面见图10。

图9 主梁半立面(单位:mm)
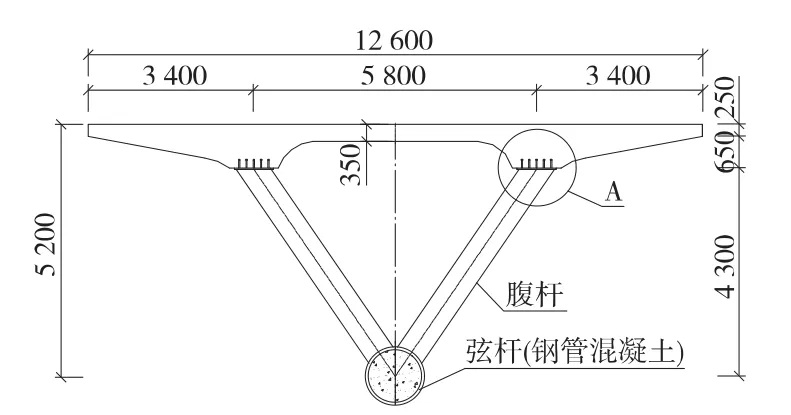
图10 主梁断面(单位:mm)
(1)轴压抗力
根据《铁路桥梁钢管混凝土结构技术规程》[2],轴压构件的强度计算公式为
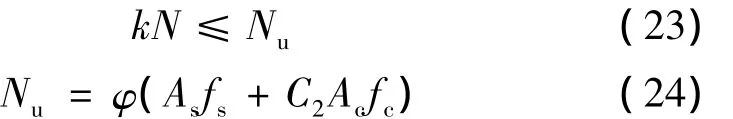
式中,k为强度安全系数;fs为钢材屈服强度;As为钢管截面面积;fc为混凝土轴心抗压强度;Ac为混凝土截面面积;φ为钢管混凝土压杆稳定系数[2,3];C2为钢管混凝土强度计算系数[2,3]。
根据前述抗力分析的影响因素,引入各随机变量,可将式(24)改写为
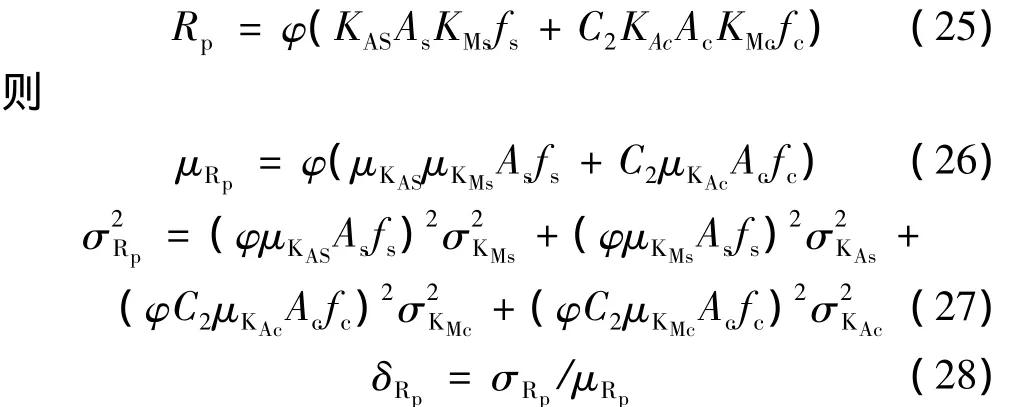
乌兰木伦河桥三角桁架钢管混凝土构件,钢管混凝土外径为1.2 m,钢管厚度为0.05 m与0.06 m两种,其中钢管材质采用Q370,混凝土强度等级为C60,则其截面抗力的均值、方差、变异系数计算见表16~表20。

表16 钢管混凝土轴压基本计算参数
根据前述影响抗力的相关随机因素,取随机参数的统计值如表17所示。

表17 钢管混凝土轴压几何及材料不定性参数

表18 未考虑计算模式不定性轴压抗力参数

表19 计算模式不定性统计参数

表20 轴压综合抗力均值与变异系数
(2)纯弯抗力
根据《铁路桥梁钢管混凝土结构技术规程》[2],纯弯构件的强度计算公式为
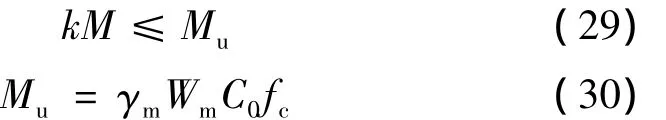
式中,k为强度安全系数;γm为钢管混凝土截面抗弯塑性发展系数[1,2];Wm为截面抗弯模量,取为πD3/32;C0为钢管混凝土强度计算系数[1,2];fc为混凝土轴心抗压强度。
同样引入几何及材料不定性随机变量,将式(30)改写为
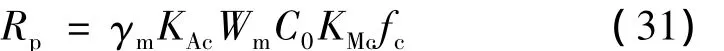
则
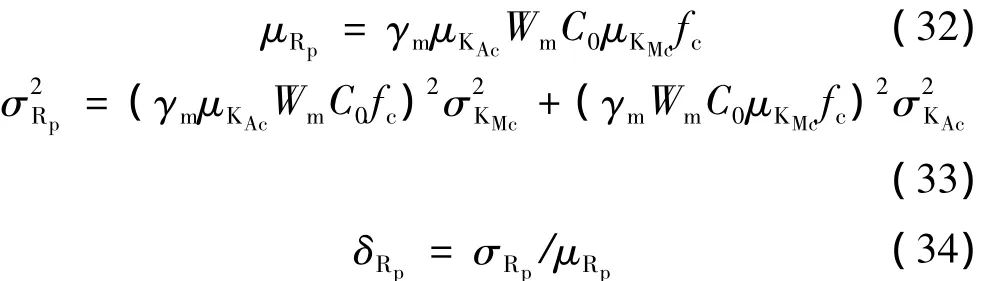
乌兰木伦河桥的截面弯曲抗力的均值、方差、变异系数计算见表21~表25。

表21 钢管混凝土抗弯基本计算参数

表22 钢管混凝土抗弯几何及材料不定性参数

表23 未考虑计算模式不定性纯弯抗力参数

表24 计算模式不定性统计参数

表25 纯弯综合抗力均值与变异系数
(3)荷载效应
恒载效应综合变量为NG,活载综合随机变量为NV,则功能函数可写为:

恒载效应表达如下
式中 KG1——恒载计算模式不定性系数;
KG2——恒载的作用系数;
KG13——自重实际荷载与理论值的比值系数;
KG23——实际二恒与理论二恒的比值。
活载效应分别可表达为

式中 Kv——动力荷载计算模式不定性系数;
Kh——实际运营活载与标准活载的比值系数;
NTk——活载产生的轴力。
恒载与活载的计算参数见表26。

表26 恒载与活载计算参数
乌兰木伦河桥的轴力、弯矩计算结果和荷载效应见表27~表30。

表27 钢管混凝土中支点截面各工况下轴力

表28 钢管混凝土中支点截面荷载效应

表29 钢管混凝土中支点截面各工况下弯矩

表30 钢管混凝土中支点截面弯矩荷载效应
(4)可靠度指标β值
利用上述自编β值计算程序,计算得到可靠性指标如表31、表32所示。

表31 钢管混凝土中支点截面轴压β值

表32 钢管混凝土中支点截面纯弯β值
7 结语
综上所述,可知:现行“预应力混凝土简支梁”(箱梁、T梁)铁道部通用设计图的可靠性指标 β值在6.37~7.63;道砟桥面“简支钢桁梁”通用设计图的杆件最小可靠性指标β值在4.65~8.34;道砟桥面“钢-混结合梁”通用设计图的可靠性指标β值在10.8~12.8;钢管混凝土连续组合梁的可靠性指标β值在4.41~6.04。
在铁路桥梁中,小桥涵、斜交刚构-连续梁以及桥面板等均采用钢筋混凝土结构,根据1991年的研究成果[4,5],这类结构的可靠性指标 β 值在 4.53 ~6.64。综合以上预应力混凝土梁、钢桁梁、钢-混凝土结合梁、钢管混凝土和钢筋混凝土结构的校准可靠性指标β值,按现行“铁路桥规”(TB10002)设计的桥梁结构能满足“可靠度桥规”[6]的要求,对于安全等级二级结构[6]的目标可靠性指标β值宜为:塑性破坏时4.2或4.5,脆性破坏时提高0.5(即4.7或5.0)。
[1]贡金鑫,魏巍巍.工程结构可靠性设计原理[M].北京:机械工业出版社,2007.
[2]中铁工程设计咨询集团有限公司.铁路桥梁钢管混凝土结构技术规程[S].北京:中铁工程设计咨询集团有限公司,2011.
[3]徐升桥.铁路桥梁钢管混凝土结构基本设计参数研究[J].铁道标准设计,2011(3):52-55。
[4]铁道部专业设计院.既有铁路钢筋混凝土梁、预应力混凝土梁正截面承载能力可靠指标校正[R].北京:铁道部专业设计院,1991.
[5]铁道部专业设计院.按现行设计规范设计的钢桥可靠指标β值的计算[R].北京:铁道部专业设计院,1991.
[6]铁道第三勘察设计院集团有限公司.铁路桥涵设计规范(送审稿)[S].天津:铁道第三勘察设计院集团有限公司,2011.

