桥梁后张预应力混凝土张拉伸长量量测与误差分析

□文/高 敏

桥梁后张预应力混凝土张拉伸长量量测与误差分析

□文/高 敏

预应力混凝土施工分为先张法和后张法。一般以伸长量及张拉应力进行控制，以张拉控制应力为主，伸长值进行校核，实际伸长值与理论伸长值误差控制在±6%以内。在实际施工中发现，后张法施工伸长值误差控制在6%以内往往难以实现。文章就后张法预应力张拉伸长量校核问题进行分析并提出一些看法。

桥梁；预应力；后张；混凝土；伸长量；测量；误差

在桥梁施工中，预应力混凝土结构因其良好的受力性能被广泛运用。预应力混凝土施工分为先张法和后张法。一般以伸长量及张拉应力进行控制，以张拉控制应力为主，伸长值进行校核，实际伸长值与理论伸长值误差控制在±6%以内。在实际施工中发现，后张法施工伸长值误差控制在±6%以内往往难以实现。

1 后张施工

桥梁后张预应力混凝土施工一直沿用油泵通过油管驱动千斤顶，千斤顶通过锚具及钢绞线对混凝土施加预应力的方法。施工时，千斤顶与工作锚接触之间设有一块限制工作锚夹片张拉过程位移的限位板，在千斤顶后设置有工具锚。钢绞线在张拉前锁紧工具锚夹片，千斤顶供油后油缸伸长拉伸钢绞线，钢绞线在张拉时工作锚夹片跟随钢绞线的拉伸，向后移动至限位板凹槽的底部，对钢绞线失去约束。当千斤顶将钢绞线张拉至设计控制张拉力，在回油放松钢绞线的瞬时，钢绞线弹性收缩，工作锚夹片跟随收缩向锚环孔内位移，随即将钢绞线锚固。

2 张拉理论伸张值确定

预应力张拉设计控制张拉力是指构件预加应力时，预应力钢筋在构件端部即锚下的控制张拉力。在理论伸长量计算时，是以钢绞线两头锚垫板之间的距离作为钢绞线的理论计算长度。一般计算式如下[1]

式中：△L为理论伸长值，mm；Pp为预应力筋的平均张拉力，N；L为预应力筋的长度，mm；Ap为预应力筋的截面面积，mm2；Ep为预应力筋的弹性模量，N/mm2。

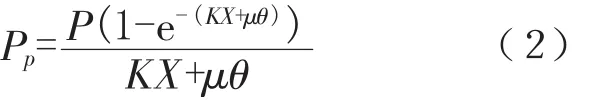
式中：P为预应力筋张拉端的张拉力，N；X为从张拉端至计算截面的孔道长度，m；θ为从张拉端至计算截面曲线孔道部分切线的夹角之和，rad；K为孔道每米局部偏差对摩擦的影响系数；μ为预应力筋与孔道壁的摩擦系数。

以某工程20 m预应力空心板梁为例，采用两端对称张拉，张拉步骤为 0→10%σcon→20%σcon→σcon（持荷 5 min）→锚固。其中，fpk=1 860 MPa，Ep=1.98×105MPa（试验数据），σcon=0.73fpk，k=0.001 5，μ=0.15。根据设计线型（见图1）将整根钢绞线分成曲线连续段及直线连续段，分段越多，计算越精确，计算过程如下。

1）0 点应力。1 860×0.73=1 357.8（MPa）。

2）1 点应力。用勾股定理求斜长

3）2点应力。8°30′=8.5×π/180=0.148 3，弧 长 0.148 3 ×14=2.076（m），摩擦系数 e-（kx+μθ）=e-（0.0015×2.076+0.15×0.1483）=0.975 0，则 2 点 应 力 为1 353.2×0.975 0=1 319.4（MPa）。

4）中点应力。孔道长1 576.2÷2=788.1（c m）=7.881（m），摩擦系数 e-（kx+μθ）=e-（0.0015×7.881）=0.988 2，则中点应力为 1 319.4×0.988 2=1 303.8（MPa）。

5）0-1段平均应力（1 357.8+1 353.2）/2=1 355.5（MPa），伸长量 1 355.5×2.275/198 000=15.57（mm）。

6）1-2段平均应力（1 353.2+1 319.4）/2=1 336.3（MPa），伸长量 1 336.3×2.076/19 8000=14.01（mm）。

7）2- 中段平均应力（1 319.4+1 303.8）/2=1 311.6（MPa），伸长量 1 311.6×7.881/198 000=52.21（mm）。

8）钢 绞 束 总 伸 长 量 （15.57+14.01+52.21）×2=163.6（mm）。

3 钢绞线预应力的量测过程

由于施工时，张拉伸长量无法在钢绞线上直接测量，故测量张拉千斤顶的油缸行程。常采用“初应力尺读数 L1”、“2 倍初应力尺读数 L2”、“终应力尺读数 L3”3次读数来量测，实际伸长值△Ls按式（3）计算[1]

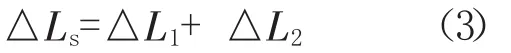
式中：△L1为从初应力到终应力间的实测伸长值；△L2为初应力以下的推算伸长值，可采用相邻级的伸长值。

3.1 工具夹片位移的量测

在钢绞线开始张拉至初始拉力时，已把松弛的预应力钢绞线拉紧，此时应将千斤顶充分固定，精确量取从千斤顶工具锚锚环外露端面至钢绞线外露夹片的长度b1。当千斤顶张拉力达到钢绞线预应力张拉设计控制拉力时，再量取从千斤顶工具锚锚环外露端面至钢绞线外露夹片的长度b2。工具夹片位移量b=b1－b2。当预应力钢绞线由很多单根组成时应对每个夹片量测，取其平均值计算，最少不得少于3根。对夹片式锚具，控制应力达到稳定锚固后，其顶面应齐平，相互间错位不宜＞2 mm。此回缩的出现对张拉伸长值的计算有影响，应减去该部分位移，即△Ls=L3＋L2－2L1-b。

3.2 千斤顶段钢绞线伸长量

钢绞线理论伸长值，是以钢绞线两头锚垫板之间的距离作为钢绞线的理论计算长度，而实际量测的是工具锚到工具锚之间钢绞线的变形量，所以还需要把千斤顶段的钢绞线伸长量 c减去，c=Pp·L/Ap·Ep，其中钢绞线长度L即为千斤顶长度，其他参数取值同式（1），则△Ls=L3＋L2－2L1－b-c。

3.3 锚固阶段回缩量

夹片式锚具锚固阶段张拉端锚具变形、预应力筋的内缩量和接缝压缩值，应不大于设计规定或≯6 mm[1]。油表回零时量取从千斤顶工具锚锚环外露端面至钢绞线外露夹片的长度b3，则有，预应力筋内缩量为终应力时尺读数－油表回零时尺读数－千斤顶段钢绞线伸长量 =（b2－b3－c）≤3 mm。但是由于锚具的压实变形以及其他一些影响伸长值的因素，这个值测得并不准。

20 m空心板梁张拉数据见表1。

表1 工程张拉数据

4 理论值与实测值的误差分析

4.1 弹性模量Ep的影响

理论伸长值计算中弹性模量Ep是决定结果的重要因素，它的取值是否正确，对计算结果的影响较大。预应力筋截面面积和弹性模量并不是固定不变的，而是由于生产批次的不同而略有起伏，一般设计给出的值都是按照国标钢绞线的弹性模量计算[2]。钢绞线的弹性模量在（195 000±10 000）MPa范围内都属正常，也就是说从185 000～205 000 MPa都是可能的。现行很多规范都要求按照实际检测弹性模量计算，如前面计算实例，试验弹性模量为198 000 MPa，总伸长量为163.6 mm。如果弹性模量取值为185 000 MPa，则钢绞束总伸长量结果如下：

1）0-1段 1 355.5×2.275/185 000=16.67（mm）；

2）1-2段 1 336.3×2.076/185 000=15.00（mm）；

3）2- 中段 1 311.6×7.881/185 000=55.87（mm）；

4）钢绞束总伸长量（16.67+15.00+55.87）×2=175.1（mm）；

5）伸长量差值 175.1-163.6=11.5（mm）；

6）偏差率 11.5/163.6×100%=7.0%。

可见工程应用中的理论伸长量计算必须按照实测值Ep进行控制，而不能用理论值Ep来计算伸长值。

4.2 系数k和μ的影响

k和μ是后张法钢绞线伸长量计算中的2个重要参数。这2个值的大小取决于管道的成型方式、力筋的类型、弯道位置及角度等因素。各个因素在施工中的变动很大，还有很多是不可能预先确定的。因此，摩擦系数的大小很大程度上取决于施工的精确程度。在工程实践中，宜对不同类型的孔道进行至少一个孔道的摩阻测试，以确保系数的准确并通过测试所确定的k和μ值宜用对设计张拉控制应力的修正。如前面计算实例，k值不变，μ取0.17，则钢绞束总伸长量结果如下：

0点应力1 357.8 MPa不变；1点应力1353.2 MPa不变；2 点摩擦系数 e-（kx+μθ）=e-（0.0015×2.076+0.17×0.1483）=0.994 4，则应力为1 353.2×0.994 4=1 345.6（MPa）；中点应力。1 345.6×0.988 2=1 329.7（MPa）；0-1 段。15.57 mm不变；1-2段平均应力（1 353.2+1 345.6）/2=1 349.4（MPa），伸长量 1 349.4×2.076/198 000=14.15（mm）；2-中段平均应力（1 345.6+1 329.7）/2=1 337.5（MPa），伸长量 1 337.5×7.881/198 000=53.24（mm）；钢绞束总伸长量（15.57+14.15+53.24）×2=165.9（mm），伸长量差值 165.9-163.6=2.3（mm），偏差率2.3/163.6×100%=1.4%。

4.3 初应力的建立

初应力时尺读数包含把松驰的预应力钢绞线拉紧和对千斤顶油制工作的调整过程，其中包含很多无效的钢绞线伸长值，所以一般以相邻级伸长值代替。但由式（4）可知初应力的建立直接影响着最后总伸长量。初应力取值较小，总伸长量偏大，初应力取值较大，总伸长量较小。初应力一般宜为张拉控制应力 σcon的10%～25%，当钢绞线束较长时，可根据适当加大初应力值。其原则是必须使钢束中所有钢绞线的张紧程度能够调整到一致且所有钢绞线的应力基本相同，以建立起最终的、准确的预应力值。实际操作中应根据钢绞线束的长度区别建立初应力值，见表2，以便更加准确的得到钢绞线的伸长量，满足应变±6%张拉控制原则的要求。

表2 不同长度的初应力

4.4 压力表读数误差

目前工程张拉时一般使用量程60 MPa，精度为1.5级的压力表，则压力表的误差绝对值为0.9 MPa。如20 m空心板梁张拉实例，N1束张拉时油表读数见表3。

表3 某梁N1束张拉时油表读数 MPa

则有A端，初应力时压力表读数相对误差为0.9/2.53×100%=35.6%，2倍初应力时压力表读数相对误差为0.9/5.16×100%=17.4%，终应力时压力表读数相对误差为0.9/25.69×100%=3.5%。

当初应力和2倍初应力时油表读数不能满足锚下的有效应力和设计张拉控制应力偏差不超±5%的规定，这种情况下其相应的尺读数也就很难满足伸长量不能超理论伸长值±6%的控制。

4.5 线性回归方程的影响

张拉用的千斤顶和压力表应配套标定、配套使用，通过给出的线性回归方程，来计算压力表读数。一般情况下在张拉力较大时比较接近线性，精确度较高，而在张拉力较小时不太接近线性，也就是通过线性方程计算出的油表的理论读数与通过试验测出的同一张拉力对应的油表实际读数有较大的差异。

5 结语

通过钢绞线伸长的工程量测实例及误差分析，可知尽管量测过程符合理论实际，但过程控制影响因素还很多。必须加强对Ep、k、μ和初应力等理论数值的量测，确定更加合理的关系方程式，使其更贴近工程实际，同时提高设备精度，减少人为误差。

[1]JTG/TF 50—2011，公路桥涵施工技术规范[S].

[2]GB/T 5224—2003，预应力混凝土用钢绞线[S].

U448.35

C

1008-3197（2013）05-54-03

10.3969/j.issn.1008-3197.2013.05.021

2013-07-30

高 敏/女，1981年出生，工程师，天津市市政公路工程质量监督站，从事公路工程质量监督工作。