圆柱形桥墩在波浪作用下的力谱与海浪谱的关系模型试验研究

□文/尚洪军 刘海源

圆柱形桥墩在波浪作用下的力谱与海浪谱的关系模型试验研究

□文/尚洪军 刘海源

随着中国桥梁建设的发展，一些跨海桥梁将建设。与在江河中建设桥梁相比，跨海桥梁结构面临的自然环境更为恶劣，潮流、台风和波浪的作用将影响结构的安全。因此研究这些因素对桥梁的作用，对桥梁结构设计有重要的意义。文章应用水池物理模型和高频率压力传感器对圆柱形桥墩在波浪作用下的受力过程进行了模拟测试。分析了波浪统计参数与波谱，受力统计参数与力谱。对力谱与波谱的关系进行了分析并给出力谱的表达式。

圆柱形；桥墩；波浪；波谱；力谱；模型

由于天然海浪的随机性，波浪往往通过2种途径进行描述。一是用海浪的统计特征参数波高和周期，一般认为天然随机波浪采用上跨零点法进行统计时，波高的概率分布符合瑞利分布。一是用海浪谱，海浪谱可用功率谱表达海浪的强度与频率关系，用方向分布函数来表达天然海浪的方向分布特征。针对这2种表达方式，波浪作用下海工建筑物的受力过程也有2种表达方式。代表特征参数波浪作用下的特殊结构物的受力有一些经验研究成果并在中国的规范和一些经典的公式中得到体现。而用谱的形式表达受力过程的特征的研究相对较少。

当研究波浪、建筑物和地基的相互作用，波浪、桥梁和上部结构的相互作用时，由于因素的复杂性以及动态响应频率的差异，应用频率分析往往是很好的途径。本文通过系列的试验研究，分析特定结构物的受力频谱与入射海浪谱之间的相互关系。研究的重点包括力谱的形式及与特征参数的关系，波浪与力谱的传递函数及传递函数中的影响因素分析。

1 试验工况

圆形截面桥墩受力试验，桥墩模型截面直径32 cm，高0.8 m，试验水深0.4 m。分6组试验来分析圆柱形桥墩所受波浪总力与入射波浪之间的关系，见表1。

表1 圆柱形桥墩波浪力试验研究波要素及组次

为减小圆柱形桥墩反射和绕射带来的边界影响，试验在12 m宽的水池中进行。为分析圆柱形桥墩与其他连接结构的频率响应，对所受力的过程进行频率分析，有以下问题需要在这一过程中加以解决：

1）圆柱形桥墩受力过程与波浪过程的对应关系；

2）力的过程与力的密度谱之间的关系；

3）波浪密度谱与力的密度谱的关系。

对于圆柱形桥墩这样一个尺度接近波长1/5～1/10的物体，所受波浪力（试验采用点压强测量与对应面积的矢量乘积和来表达波浪力，测点为8列，每列7个传感器）的方向往往与迎浪侧波面高程与背浪侧波面高程有关。如果对于一个同步测量的时间过程，将迎浪侧波峰受力表达为正，将波面高于静水面表达为正，则波面要滞后于力的过程。圆柱形桥墩受力过程与波浪过程的对应关系，就与圆柱形桥墩直径与波长的比值有关。

2 试验结果

力谱所要表达的是力的能量在频率上的分布，这里所有的试验都是针对圆柱形桥墩完全刚性而言的，因此力的能量在频率上的分布会与波浪的能量在频率上的分布具有很强的相关性。然而受波浪作用面积的不对称影响，应用基于谐波理论的密度谱时，过程的统计参数与力谱之间可能会存在不协调的问题，此时可能需要叠加一个虚波或者调整零点来实现。

如果力谱能够表达力的过程，那么从波谱到力谱是一个经验性的传递函数，其参数主要包括波浪要素、墩的尺度以及水深等。

取试验水深 40 cm；试验波要素：H13%=0.1 m；T1/3=1.57 s。试验结果见图1-图4。

对6组不同波浪要素试验的各3次重复过程均值进行统计分析。结果见表2-表5。

表2 波浪特征值

表3 波压力特征值

表4 波谱特征值

表5 力谱特征值

以上表格M0、M1和M2分别表示波谱（力谱）的零阶矩，一阶矩和二阶矩。F1%、F13%、Fmean与相对应的波高相类似，即图5中波压力过程线累积频率为 1%，13%的统计波浪力，是峰值与谷值之差。而+XFmax是指 X正方向最大波浪力峰值，-XFmax指X负方向最大波浪力峰值。

图5 力的特征值定义

3 结果分析

通过波谱和力谱的对比分析可以看出，力谱与JONSWAP谱有很强的一致性。这里主要分析特征波高与特征力之间的关系，从而把这种关系进一步推进至谱之间的关系，见图6-图8。

当运用力谱模拟力的过程时，应对比该力的过程和实测过程与统计值之间的关系，因为试验情况并不具有广泛的代表性。分析2个过程在相位上的差别，不仅仅是波浪的传播时间，还在于当波峰到达墩的哪个时刻，正向力最大；波谷到达墩的哪个时刻，负向力最大。这些都是可基于本文所涉及的试验但需要进一步深入的内容。

JTS 145-2—2013《海港水文规范》对圆墩波浪力的计算有算式。由于圆柱形桥墩在波浪作用下的受力有许多研究成果，这些成果往往对应于不同的试验研究条件，这里不考虑这些力值的变化，不同的参数可以通过比尺变化来得到对应的波浪力。这里依据谱形状对谱参数进行修正。

根据试验的结果，按照压力过程统计得到的力的统计值将其替换JONSWAP中的波高值，同时将力过程统计的相应周期带入JONSWAP谱算式并调整谱峰因子，得到的力谱对应的数值，见图9。

图9 调整谱峰因子得到的力谱计算值和实测值

可见调整谱峰因子后得到很好地拟合效果，将各组次的拟合谱峰因子列于表6。

表6 圆形截面桥墩力谱谱峰因子拟合值

通过以上分析，得到圆形截面桥墩在随机台风浪和涌浪作用下的力谱表达式

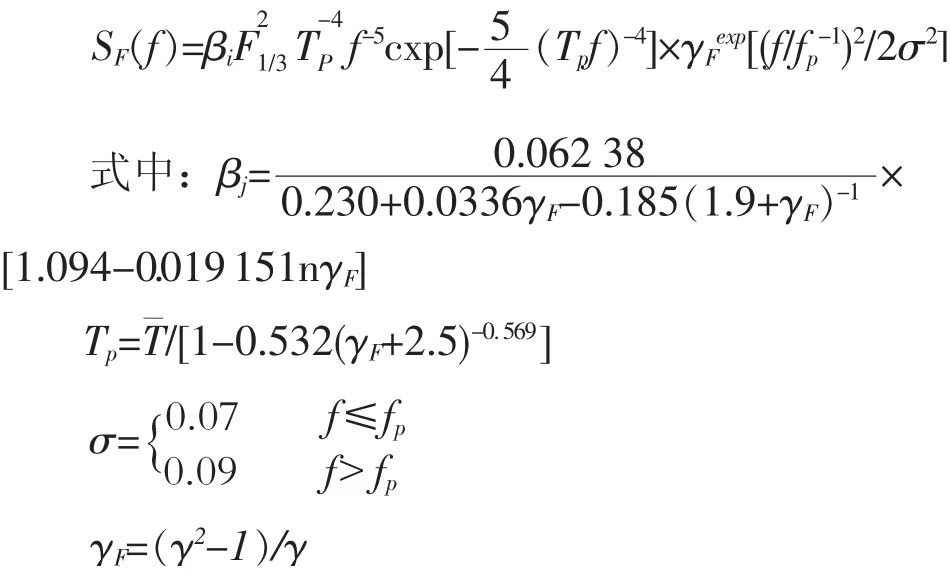
其中：γ为波浪谱峰因子，γF为力谱谱峰因子，fp是峰频，为谱峰频周期TP的倒数，SF（f）为力谱谱密度，F1/3为力过程统计有效峰值的2倍，是累积出现频率为33%的均值的2倍（即力过程峰值由大到小排列得到力的序列,取整个序列前1/3峰值的平均值作为该序列有效峰值,F1/3等于该有效峰值的2倍），f为频率，为与波浪相同的平均周期。

4 结论

1）研究力过程的谱特征是讨论波浪、建筑物和地基的相互作用，研究波浪、桥梁和上部结构的相互作用以及动态响应频率的良好途径。

2）对于试验中的JONSWAP波谱，力谱与波谱的频率分布有很接近的大小关系。

3）调整谱峰因子可以得到很好的力谱拟合效果，给出了基于JONSWAP的力谱表达式。

4）力特征值与力谱关系同波浪特征值与波谱的关系相比，力的特征值有更大的离散。

［1］Sui S F.The regular wave spectrum and an analytical method of superposition of wave spectrum［J］.Tropic Oceanology,1984，（8）：2-9.

［2］Li Y C.The influent of directional energy spread on the retraction of wave spectrum under the action of current and sea bed［J］.Coastal Engineering,1989,（12）：17-29.

［3］Wei J Q,Gu M,Hui C,etc.Research of 3D wave’s directional spectrum estimation ［J］.Journal of ship mechanics,2003，（10）：11-20.

［4］Wang Y Z,Hong N N,Tang Z P.A method for dynamic analysis of caisson breakwater based on wave spectrum theory［J］.The Coastal Engineering,2007,（8）：1-6.

［5］Teng B,Li Y C.Wave force spectrum on horizontal bar［J］.Marine Science Bulletin,198,（2）：27-35.

［6］Jang D C,Tai W T,Lou S L.Research on diffraction and refraction of wave power spectrum［J］.Acta Oceanologica Sinica,1993,（9）：120-129.

□刘海源/交通运输部天津水运工程科学研究所。

U443.22

C

1008-3197（2013）05-60-04

10.3969/j.issn.1008-3197.2013.05.023

2013-06-03

尚洪军/男，1977年出生，工程师，天津临港投资控股有限公司，主要从事港口海岸工程建设和管理。