独立于应用的数据库聚类技术
程文琛, 胡学钢
(合肥工业大学 计算机与信息学院,安徽 合肥 230009)
一个大型组织拥有多个分支,每个分支有本地数据库。如果将全部分支的数据库合并成一个大数据库,然后挖掘这个大数据库,则存在如下问题:
(1)网络传输安全性低,且通信代价高。
(2)数据总量庞大,磁盘挖掘算法效率低。
(3)全部分支数据汇总成一张大表,表的属性个数非常多,使用Apriori算法挖掘会形成组合爆炸;表中存在很多缺失值,无法设置最小支持度等挖掘指标。
上述3个缺陷使得简单合并数据库的挖掘方法不可行,多数据库挖掘技术[1]必须重新设计。
面向应用的数据库选择合并挖掘技术[2]必须针对具体的每一个应用遍历一次所有的数据库,方法效率低下。而分布式并行挖掘技术[3]不产生中间规则,并行算法部署困难。
事实上,多数据库挖掘过程满足一般的数据挖掘过程。首先必须进行数据准备工作,除了数据清洗,消除属性歧义等步骤,最重要的是根据数据库间相似度对多数据库进行划分[4-5]。
1 数据库间相似度
1.1 多数据库特征
(1)存在若干个事务类型,每个事务类型包括1个或多个数据库。
(2)隶属于同一个事务类型的多个数据库之间有着密切的关系,它们都反映该事务的本质,包含着许多共有事务项,又根据本地的实际情况扩展或简化了一些事务项。
(3)隶属于同一个事务的每个数据库包含的事务项个数不等。
(4)隶属于不同事务的数据库间共有事务项很少,因为很少相同事务项反映不同事务类型。
(5)相似度能很好地反映数据库间的关系。
用特征指代对象是一种通用技术。因此,能通过比较2个数据库的特征集来测量数据库间的相似度。数据库类型多样,本文针对的是事务数据库,事务数据库的属性集(也可以是关联规则集的属性集)能够当作其特征来指代该数据库(大型数据库特征集可以用抽样技术[6]获得)。2个事务数据库的属性集可以被看作非对称二元变量[7],2个事务数据库的相似度可以采用非对称二元变量的相似度计算方法得到。
1.2 相似度测量
多个数据库的属性结构用二元属性描述的关系见表1所列。

表1 用二元属性描述的多数据库结构
表1说明了给定m个数据库,所有数据库属性并集长度为L的属性包含情况。Y表示该数据库包含此属性,N表示该数据库不包含此属性。任意2个数据库Di和Dj的相似度测量公式如下:

其中,系数sim(i,j)称作Jaccard系数;q表示Di、Dj都包含的属性个数;r表示Di包含、Dj不包含的属性个数;s表示Dj包含、Di不包含的属性个数。不计Di、Dj都不包含的属性个数。
若数据库的特征是与关联规则集有关的属性项集,则仍然可以采用sim(i,j)表示任意2个数据库Di和Dj的相似度。其中q表示Di、Dj的关联规则集都包含的属性个数;r表示Di的关联规则集包含、Dj的关联规则集不包含的属性个数;s表示Dj的关联规则集包含、Di的关联规则集不包含的属性个数;(1)式不计Di、Dj的关联规则集都不包含的属性个数。
关联规则集相关的相似度测量方法受事务记录的影响较大,得到的相似度值较低,因此本文的实验采用直接属性项集相似度测量方法。
2 多数据库的最优划分
2.1 多数据库完全划分与簇中心
分裂层次聚类[8]首先将所有对象置于一个簇中,然后将它逐步细分为越来越小的簇,直到每个对象自成一簇。在没有给定具体终止条件的情况下,任何一次分裂满足以下4个条件(α为分裂阈值):
(2)对于clusterk中任意2个数据库Di和Dj,sim(i,j)≥α。
设D是M个数据库D1,D2,…,Dm的集合。若满足上述4个条件,则该划分是测度sim下的一个完全划分。
一个完全划分中,每个数据库只属于一个簇,且必须属于一个簇。按照不同的α值得到不同的完全划分或不完全划分。当α=0或α=1时,多数据库划分为1个簇或m个簇,可以得到2个完全划分,这2个完全划分称为平凡划分;其他完全划分称为非平凡划分。
m个对象通过k中心点法[9]得到k个簇,每个簇选出一个对象作为簇中心。同理,m个数据库对于给定阈值α的完全划分有c个簇,且数据库的特征向量是分类数据,则可采用最大树方法得到对应的簇中心。
定义1 簇的最大树是簇内一个数据库与其他数据库之间的相似度和T最大的所有边和所有数据库构成的树。
该数据库是这棵最大树的根,簇的最大树的高度是2,如图1所示。一个簇可能存在多棵最大树;簇的所有最大树的根集合是簇中心候选集,如图2所示,图2中,该簇的簇中心候选集是{D1,D2}。如果簇只有一棵最大树,那么这棵最大树的根就是这个簇的簇中心。只有一棵最大树的簇的簇中心候选集就是包含唯一最大树根的集合。多数情况中,簇的最大树是唯一的。

图1 簇的最大树

图2 一个簇的不同最大树
2.2 多数据库最优划分
m个数据库D1,D2,…,Dm一次完全划分产生的簇中心候选集的集合中,每个簇的候选簇中心的所有不同组合中,使S取最小值的组合就是本次完全划分的聚类中心,同时该S值就是本次完全划分的评价值[10-11],即

根据AFCMC算法可得,m个数据库D1,D2,…,Dm最优划分的S值是所有完全划分的S值中的最小值,m个数据库D1,D2,…,Dm的最优划分可以通过搜索所有完全划分的评价值的最小S值确定。
当m个数据库的非平凡完全划分不存在时,必须选择一种平凡划分。如果选择Cluster0,S值取+∞,因此,只能选择Cluster1,将每个数据库划分成一个簇。
2.3 最优划分算法
BestPartition程序如下:

程序BestPartition搜索m个给定数据库D1,D2,…,Dm所有的完全划分中的最优划分。步骤(1)初始化,创建相似度关系表。步骤(2)根据相似度关系表创建相似度序列,该序列按从小到大的顺序对表中的相似度无重复地排序。步骤(3)根据相似度序列中相似度先后顺序,对给定数据库进行划分,若能得到完全划分,计算该次完全划分的S值。步骤(4)查找所有完全划分的S值中最小S值。步骤(5)输出最小S值对应的完全划分。
3 实验与分析
BestPartition程序已经使用Java语言开发完成,实验条件是双核处理器2.8GHz,内存2G的Acer台式PC。
3.1 聚类算法时间性能比较
根据多个事务数据库的特点,并且参照著名的蘑菇数据集,合成一个200条记录的数据集。数据集中的每条记录表示一个事务数据库的项集,记录的长度不相等,大约为30。记录的项表示事务的项,用英文字母表示。数据集经过标记后有60个簇,每个簇的数据库个数为2~9。数据集的规模和内部结构与实际应用比较接近。
合成数据集的参数没有作为先验知识用于设置实验算法的参数;KMediods的k值遍历1~200,DBSCAN的minPts设为1,DIANA的α值和DBSCAN的ε值遍历相似度表中所有不同的值。
使用sim(i,j)得到数据集的相似度表,采用DIANA、KMediods和DBSCAN 3种算法进行聚类时间性能比较,结果如图3所示。

图3 聚类算法时间性能比较
由图3可知,KMediods的时间增长非常快,$KMediods限定了聚类的个数处于的大致区间,情况仍然比较糟糕,这是由于算法的时间复杂度和缺乏先验知识造成的;DBSCAN的时间略高于DIANA。KMediods和DBSCAN得到的聚类结果都包含预先标记的聚类结果,但是都产生了过多的错误聚类;在没有给定k值的前提下,KMediods遍历了所有可能的k取值,显然使用该方法选取多数据库进行分组是不可行的;DBSCAN获得的聚类结果是重复的,多次聚类了高阈值的不完全划分,与低阈值的完全划分是重复的,而评价重复的划分没有任何意义,因此该方法比DIANA要差一些。DIANA很好地符合了多数据库的特点,因此它是最高效的聚类算法,这就是选择DIANA的原因。
3.2 应用实例
实验数据来自http://www.kdnuggets.com/网站的真实数据集,包括DB1、DB2、DB3、DB4、DB5、DB66个数据库。其中,DB1、DB2来自博物馆;DB3、DB4、DB5、DB6来自银行。6个数据库的参数比较接近,属性个数约为300,记录条数约为10 000,相似(异)度见表2、表3所列。
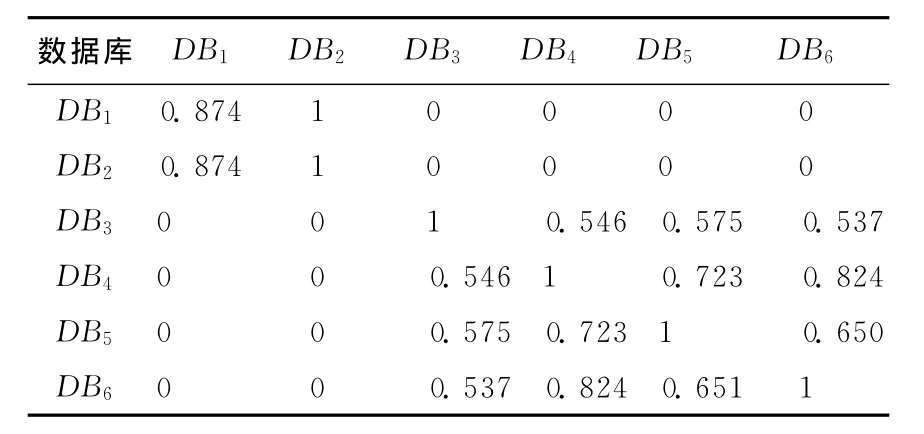
表2 测度sim下6个数据库的相似度
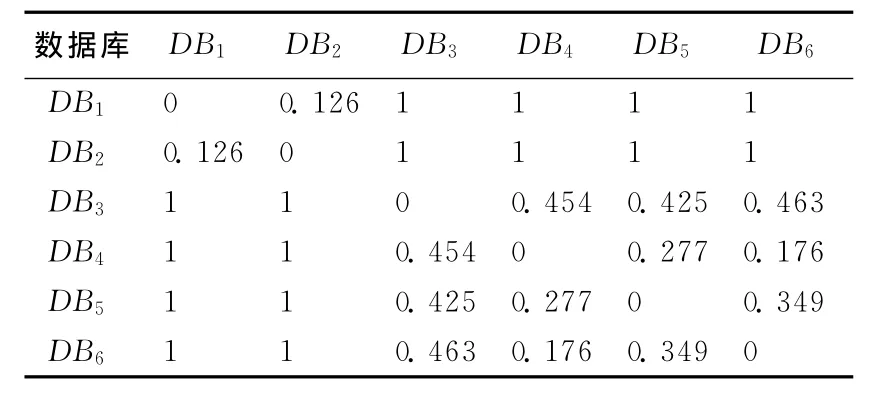
表3 测度sim下6个数据库的相异度
程序BestPartition根据相似(异)度表计算得到6个数据库所有的划分和S值,见表4所列。

表4 程序BestPartition运行结果
表4中,“-”表示对该阈值α没有完全划分,因此没有S值。
程序BestPartition通过搜索所有S值得到:当阈 值 α =0.537,最 优 划 分同时还可以得到最优划分的聚类中心为{{D1},{D4}},相应的隶属度(membership)矩阵见表5所列,最优划分如图4所示。

表5 最优划分对应的隶属度矩阵
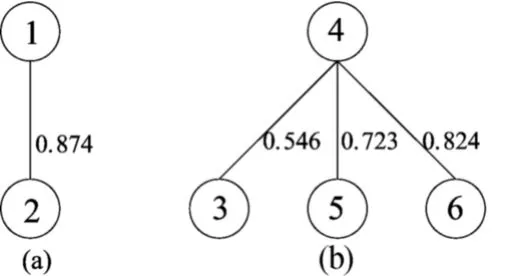
图4 6个数据库的最优划分
上述实验结果证实了来自博物馆的数据库DB1、DB2与来自银行的数据库DB3、DB4、DB5、DB6是不相关的,最优划分与实际情况完全吻合,程序运行时间为0.001 3s。该实验成功证明了本文提出的多数据库的最优划分方法是正确的。
3.3 最优划分时间性能比较
由于相似度矩阵的复杂性和簇中心候选集组合次数的不确定性,多数据库最优划分的时间复杂度很难估计;图5所示为聚类中心组合次数对多数据库最优划分过程消耗时间的影响(使用了2个合成数据集,不包括相似度计算时间)。

图5 最优划分时间比较
通过观察实验结果可以看出,最优分组与预先的数据标记完全一致,没有产生错误率。96条记录以内,消耗的时间非常少;随着聚类中心组合次数的增加,记录条数达到96~112范围内,消耗的时间稍有增加;超过112条记录,时间迅速增长,但仍然可接受。因此可以得出如下结论:
(1)多数据库最优分组方法是正确的,得到全局最优解。
(2)最优分组方法的时间效率很高,适合实际应用中的小规模数据集,即使在聚类中心组合次数很多的情况下,算法的时间仍然是可接受的。
(3)通过减少聚类中心的组合次数可以有效地降低算法的运行时间,该算法具有较好的扩展性。
(4)该算法不依赖先验知识,具有较高的自适应性,是Chameleon等方法无法比较的。
4 结束语
多数据库挖掘过程分为3个阶段:① 数据库划分;② 挖掘单个数据库;③ 规则分析与合成。数据库聚类技术是多数据库挖掘系统中的一个关键技术。本文提出的划分策略搜索代价较低,能提高多数据库挖掘系统的性能;给设计应用独立的多数据库挖掘系统提供了一条途径,具有较高的理论实用价值。下一步研究将注重数据库间相似度、距离测量方法和隶属函数及模糊指数确定方法。
[1]Zhang Shichao,Zhang Chengqi,Wu Xindong.Knowledge discovery in multiple databases[M].Springer,2004:79-135.
[2]Liu H,Lu H,Yao J.Identifying relevent databases for multi-databases mining[C]//Proceedings of the Second Pacific-Asia Conference on Knowledge Discovery and Data mining,April 15-18,1998:210-221.
[3]Cheung D,Ng V,Fu A,et al.Efficient mining of association rules in distributed databases[J].IEEE Transactions on Knowledge and Data Engineering,1996,8 (6):911-922.
[4]Wu Xindong,Zhang Chengqi,Zhang Shichao.Database classification for multi-database mining[J].Information System,2005,30:71-88.
[5]曹 慧.一种基于聚类的多数据库分类方法设计[J].网络安全技术与应用,2010(6):79-81.
[6]Zhang S,Zhang C.Estimating itemsets of interest by sampling[C]//Proceedings of the 10th IEEE International Conference on Fuzzy Systems,2001:131-134.
[7]Han Jiawei,Kamber M.数据挖掘概念与技术[M].第2版.范 明,孟小峰,译.北京:机械工业出版社,2007:255-256.
[8]陈黎飞,姜青山,王声瑞.基于层次划分的最佳聚类数确定方法[J].软件学报,2008,19(1):62-72.
[9]刘金岭.k中心点聚类算法在层次数据的应用[J].计算机工程与设计,2008,29(24):6418-6422.
[10]熊和金,陈德军.智能信息处理[M].北京:国防工业出版社,2006:12-14.
[11]李为民,朱永峰,付 强.基于自适应模糊聚类分析的目标冗余信息处理[J].计算机应用,2005,25(4):949-951.
[12]刘小芳,何彬彬.近邻样本密度和隶属度加权FCM算法的遥感图像分类方法[J].仪器仪表学报,2011,32(10):2242-2247.
[13]高新波,裴继红,谢维信.模糊C-均值聚类算法中加权指数M的研究[J].电子学报,2000,28(4):80-84.

